沪科版数学八年级上册同步课时练习:13.1.3 三角形中几条重要线段(word版含答案)
文档属性
| 名称 | 沪科版数学八年级上册同步课时练习:13.1.3 三角形中几条重要线段(word版含答案) | 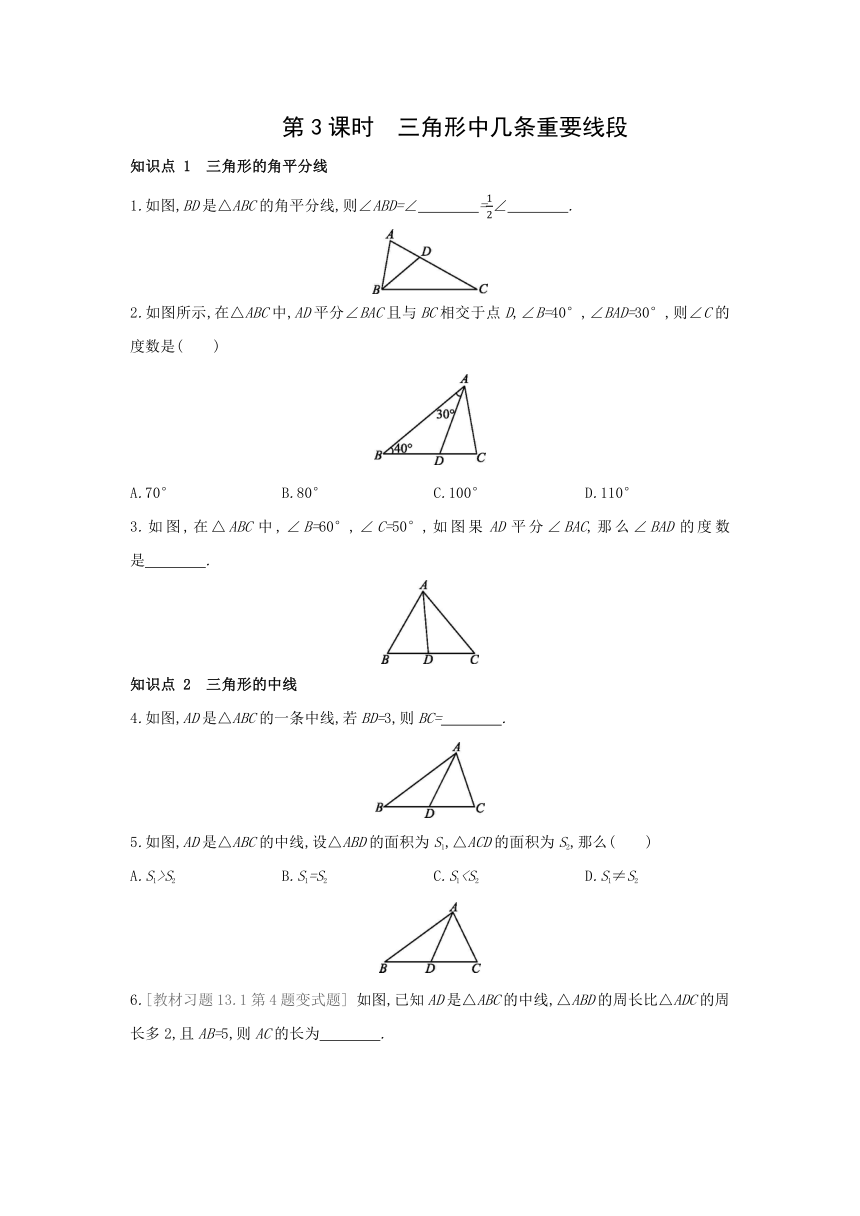 | |
| 格式 | docx | ||
| 文件大小 | 251.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 16:46:06 | ||
图片预览



文档简介
第3课时 三角形中几条重要线段
知识点 1 三角形的角平分线
1.如图,BD是△ABC的角平分线,则∠ABD=∠ =∠ .
2.如图所示,在△ABC中,AD平分∠BAC且与BC相交于点D,∠B=40°,∠BAD=30°,则∠C的度数是( )
A.70° B.80° C.100° D.110°
3.如图,在△ABC中,∠B=60°,∠C=50°,如图果AD平分∠BAC,那么∠BAD的度数是 .
知识点 2 三角形的中线
4.如图,AD是△ABC的一条中线,若BD=3,则BC= .
5.如图,AD是△ABC的中线,设△ABD的面积为S1,△ACD的面积为S2,那么( )
A.S1>S2 B.S1=S2 C.S16.[教材习题13.1第4题变式题] 如图,已知AD是△ABC的中线,△ABD的周长比△ADC的周长多2,且AB=5,则AC的长为 .
知识点 3 三角形的高
7.[教材练习第3题变式题] 如图,用三角尺作△ABC的边AB上的高线,下列三角尺的摆放位置正确的是( )
8.三角形的三条高所在的直线相交于三角形的顶点,这个三角形的形状是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
9.如图,已知CD是△ABC的一条高,请你再画出另外两条高.
知识点 4 三角形的重心
10.如图,AD,BE是△ABC的两条中线,交点为G,连接CG并延长交AB边于点F.下列结论中正确的有 .(将所有正确结论的序号都填写在横线上)
①G是△ABC的重心; ②CF⊥AB; ③CF平分∠ACB; ④BF=AF.
11.下列说法错误的是( )
A.三角形的三条中线都能平分三角形的面积
B.三角形的三条角平分线交于三角形内一点
C.三角形的三条高交于一点
D.三角形的中线、角平分线、高都是线段
12.如图所示,D是∠ABC的平分线BD和∠ACB的平分线CD的交点.若∠A=50°,则∠D的度数为( )
A.120° B.130° C.115° D.110°
13.如图,在△ABC中,BD为△ABC的角平分线,CE为△ABC的高,CE,BD交于点F,∠A=50°,∠BCA=60°,那么∠BFC的度数是( )
A.115° B.120° C.125° D.130°
14.如图,AD是△ABC的中线,CE是△ACD的中线,S△ACE=3 cm2,则S△ABC= cm2.
15.在△ABC中,∠A=40°,BD是边AC上的高.若∠CBD=15°,则∠ABC的度数是 .
16.[教材习题13.1第4题变式题] 在△ABC中,AB=AC,AC边上的中线BD把△ABC的周长分为24 cm和30 cm的两部分,求△ABC各边的长.
17.[教材习题13.1第6题变式题] 如图,在△ABC中,∠BAC的平分线交BC于点D,∠B=65°,∠C=50°,DE是△ABD的高,求∠ADE的度数.
18.如图,网格中每个小正方形的边长都为1.在△ABC中,试画出三边的中线,这三条中线是否交于一点 若交于一点,则这点把每条中线分成的两段有什么关系
19.如图所示,已知AD,AE分别是△ABC的高和中线,AB=8 cm,AC=15 cm,BC=17 cm,∠BAC=90°.试求:
(1)AD的长;
(2)△ACE和△ABE的周长的差;
(3)△ABE的面积.
答案
1.CBD ABC
2.B 解: 利用角平分线的性质与三角形内角和为180°可求得.
3.35° 解: 在△ABC中,∠B=60°,∠C=50°,
所以∠BAC=180°-60°-50°=70°.
因为AD平分∠BAC,
所以∠BAD=∠BAC=35°.
4.6
5.B
6.3 解: 因为AD是BC边上的中线,所以BD=CD,
所以△ABD的周长-△ADC的周长=AB-AC.
因为△ABD的周长比△ADC的周长多2,且AB=5.
所以AB-AC=2,即AC=3.
7.B 解: 过顶点C作AB的垂线段,只有B项正确.
8.B 解: 锐角三角形的三条高交于三角形内,直角三角形的三条高交于三角形的直角顶点处,钝角三角形的三条高所在的直线交于三角形外一点.
9.解:如图,所画线段AN,BM即为所求.
10.①④
11.C 解: 根据三角形的高线、角平分线、中线的定义对各选项分析判断.A项,三角形的中线都平分它的面积,故本选项说法正确;B项,三角形的三条角平分线交于三角形内一点,故本选项说法正确;C项,三角形的三条高所在的直线交于一点,而三条高不一定相交,故本选项说法错误;D项,三角形的中线、角平分线、高都是线段,故本选项说法正确.
12.C 解: 因为∠A=50°,
所以∠ABC+∠ACB=180°-∠A=180°-50°=130°.
因为D是∠ABC的平分线BD和∠ACB的平分线CD的交点,
所以∠DBC+∠DCB=(∠ABC+∠ACB)=×130°=65°.
在△BCD中,∠D=180°-(∠DBC+∠DCB)=180°-65°=115°.
故选C.
13.C
14.12 解: 因为AD,CE分别是△ABC,△ACD的中线,所以S△DEC=S△ACE=3 cm2.所以S△ABD=S△ACD=6 cm2.所以S△ABC=12 cm2.
15.65°或35° 解: 如图①,当BD在△ABC内部时,∠ABD=180°-90°-∠A=50°,则∠ABC=∠ABD+∠CBD=50°+15°=65°;如图②,当BD在△ABC外部时,∠ABD=180°-90°-∠A=50°,则∠ABC=∠ABD-∠CBD=50°-15°=35°.
① ②
16.解:设AB=AC=x cm,BC=y cm.
由题意可知或
解得或
经检验,均符合题意.
因此三角形各边的长有两种情况:①AB=AC=16 cm,BC=22 cm;②AB=AC=20 cm,BC=14 cm.
17.解:因为∠B=65°,∠C=50°,
所以∠BAC=65°.
因为AD是△ABC的角平分线,
所以∠BAD=∠BAC=32.5°.
又因为DE是△ABD的高,
所以∠AED=90°.
所以∠ADE=180°-90°-32.5°=57.5°.
18.解:如图,三条中线交于一点,该点叫三角形的重心.在同一条中线上,重心到边的中点的距离等于它到顶点距离的一半.
19.解:(1)因为∠BAC=90°,AD是边BC上的高,
所以AB·AC=BC·AD,
所以AD===(cm),
即AD的长为 cm.
(2)因为AE为BC边上的中线,
所以BE=CE,
所以△ACE的周长-△ABE的周长=AC+AE+CE-(AB+BE+AE)=AC-AB=15-8=7(cm),
即△ACE和△ABE的周长的差是7 cm.
(3)因为△ABC是直角三角形,∠BAC=90°,AB=8 cm,AC=15 cm,
所以S△ABC=AB·AC=×8×15=60(cm2).
因为AE是边BC上的中线,
所以BE=EC,
所以BE·AD=EC·AD,
即S△ABE=S△AEC,
所以S△ABE=S△ABC=30(cm2),
即△ABE的面积是30 cm2.
知识点 1 三角形的角平分线
1.如图,BD是△ABC的角平分线,则∠ABD=∠ =∠ .
2.如图所示,在△ABC中,AD平分∠BAC且与BC相交于点D,∠B=40°,∠BAD=30°,则∠C的度数是( )
A.70° B.80° C.100° D.110°
3.如图,在△ABC中,∠B=60°,∠C=50°,如图果AD平分∠BAC,那么∠BAD的度数是 .
知识点 2 三角形的中线
4.如图,AD是△ABC的一条中线,若BD=3,则BC= .
5.如图,AD是△ABC的中线,设△ABD的面积为S1,△ACD的面积为S2,那么( )
A.S1>S2 B.S1=S2 C.S1
知识点 3 三角形的高
7.[教材练习第3题变式题] 如图,用三角尺作△ABC的边AB上的高线,下列三角尺的摆放位置正确的是( )
8.三角形的三条高所在的直线相交于三角形的顶点,这个三角形的形状是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
9.如图,已知CD是△ABC的一条高,请你再画出另外两条高.
知识点 4 三角形的重心
10.如图,AD,BE是△ABC的两条中线,交点为G,连接CG并延长交AB边于点F.下列结论中正确的有 .(将所有正确结论的序号都填写在横线上)
①G是△ABC的重心; ②CF⊥AB; ③CF平分∠ACB; ④BF=AF.
11.下列说法错误的是( )
A.三角形的三条中线都能平分三角形的面积
B.三角形的三条角平分线交于三角形内一点
C.三角形的三条高交于一点
D.三角形的中线、角平分线、高都是线段
12.如图所示,D是∠ABC的平分线BD和∠ACB的平分线CD的交点.若∠A=50°,则∠D的度数为( )
A.120° B.130° C.115° D.110°
13.如图,在△ABC中,BD为△ABC的角平分线,CE为△ABC的高,CE,BD交于点F,∠A=50°,∠BCA=60°,那么∠BFC的度数是( )
A.115° B.120° C.125° D.130°
14.如图,AD是△ABC的中线,CE是△ACD的中线,S△ACE=3 cm2,则S△ABC= cm2.
15.在△ABC中,∠A=40°,BD是边AC上的高.若∠CBD=15°,则∠ABC的度数是 .
16.[教材习题13.1第4题变式题] 在△ABC中,AB=AC,AC边上的中线BD把△ABC的周长分为24 cm和30 cm的两部分,求△ABC各边的长.
17.[教材习题13.1第6题变式题] 如图,在△ABC中,∠BAC的平分线交BC于点D,∠B=65°,∠C=50°,DE是△ABD的高,求∠ADE的度数.
18.如图,网格中每个小正方形的边长都为1.在△ABC中,试画出三边的中线,这三条中线是否交于一点 若交于一点,则这点把每条中线分成的两段有什么关系
19.如图所示,已知AD,AE分别是△ABC的高和中线,AB=8 cm,AC=15 cm,BC=17 cm,∠BAC=90°.试求:
(1)AD的长;
(2)△ACE和△ABE的周长的差;
(3)△ABE的面积.
答案
1.CBD ABC
2.B 解: 利用角平分线的性质与三角形内角和为180°可求得.
3.35° 解: 在△ABC中,∠B=60°,∠C=50°,
所以∠BAC=180°-60°-50°=70°.
因为AD平分∠BAC,
所以∠BAD=∠BAC=35°.
4.6
5.B
6.3 解: 因为AD是BC边上的中线,所以BD=CD,
所以△ABD的周长-△ADC的周长=AB-AC.
因为△ABD的周长比△ADC的周长多2,且AB=5.
所以AB-AC=2,即AC=3.
7.B 解: 过顶点C作AB的垂线段,只有B项正确.
8.B 解: 锐角三角形的三条高交于三角形内,直角三角形的三条高交于三角形的直角顶点处,钝角三角形的三条高所在的直线交于三角形外一点.
9.解:如图,所画线段AN,BM即为所求.
10.①④
11.C 解: 根据三角形的高线、角平分线、中线的定义对各选项分析判断.A项,三角形的中线都平分它的面积,故本选项说法正确;B项,三角形的三条角平分线交于三角形内一点,故本选项说法正确;C项,三角形的三条高所在的直线交于一点,而三条高不一定相交,故本选项说法错误;D项,三角形的中线、角平分线、高都是线段,故本选项说法正确.
12.C 解: 因为∠A=50°,
所以∠ABC+∠ACB=180°-∠A=180°-50°=130°.
因为D是∠ABC的平分线BD和∠ACB的平分线CD的交点,
所以∠DBC+∠DCB=(∠ABC+∠ACB)=×130°=65°.
在△BCD中,∠D=180°-(∠DBC+∠DCB)=180°-65°=115°.
故选C.
13.C
14.12 解: 因为AD,CE分别是△ABC,△ACD的中线,所以S△DEC=S△ACE=3 cm2.所以S△ABD=S△ACD=6 cm2.所以S△ABC=12 cm2.
15.65°或35° 解: 如图①,当BD在△ABC内部时,∠ABD=180°-90°-∠A=50°,则∠ABC=∠ABD+∠CBD=50°+15°=65°;如图②,当BD在△ABC外部时,∠ABD=180°-90°-∠A=50°,则∠ABC=∠ABD-∠CBD=50°-15°=35°.
① ②
16.解:设AB=AC=x cm,BC=y cm.
由题意可知或
解得或
经检验,均符合题意.
因此三角形各边的长有两种情况:①AB=AC=16 cm,BC=22 cm;②AB=AC=20 cm,BC=14 cm.
17.解:因为∠B=65°,∠C=50°,
所以∠BAC=65°.
因为AD是△ABC的角平分线,
所以∠BAD=∠BAC=32.5°.
又因为DE是△ABD的高,
所以∠AED=90°.
所以∠ADE=180°-90°-32.5°=57.5°.
18.解:如图,三条中线交于一点,该点叫三角形的重心.在同一条中线上,重心到边的中点的距离等于它到顶点距离的一半.
19.解:(1)因为∠BAC=90°,AD是边BC上的高,
所以AB·AC=BC·AD,
所以AD===(cm),
即AD的长为 cm.
(2)因为AE为BC边上的中线,
所以BE=CE,
所以△ACE的周长-△ABE的周长=AC+AE+CE-(AB+BE+AE)=AC-AB=15-8=7(cm),
即△ACE和△ABE的周长的差是7 cm.
(3)因为△ABC是直角三角形,∠BAC=90°,AB=8 cm,AC=15 cm,
所以S△ABC=AB·AC=×8×15=60(cm2).
因为AE是边BC上的中线,
所以BE=EC,
所以BE·AD=EC·AD,
即S△ABE=S△AEC,
所以S△ABE=S△ABC=30(cm2),
即△ABE的面积是30 cm2.
