沪科版数学八年级上册13.1 第2课时 三角形中角的关系 同步课时练习(word版 含解析)
文档属性
| 名称 | 沪科版数学八年级上册13.1 第2课时 三角形中角的关系 同步课时练习(word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 181.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 16:49:07 | ||
图片预览

文档简介
第2课时 三角形中角的关系
知识点 1 三角形按角的大小分类
1.若一个三角形的三个内角的度数分别是80°,60°,40°,则这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
2.在△ABC中,∠A比∠B大100°,则△ABC的形状是( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.无法判断
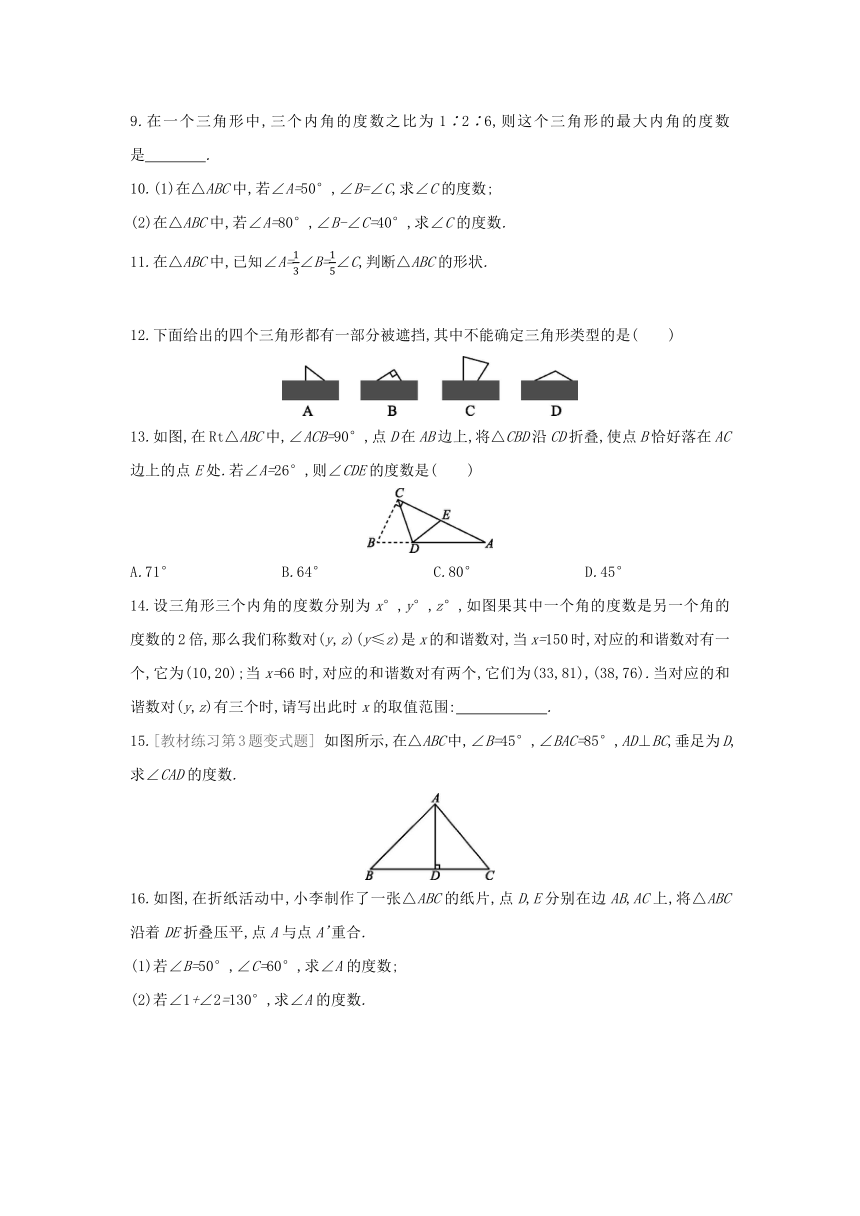
3.如图示,中有 个直角三角形,其中BC是△ABC的 边,BC是△BCD的 边.
知识点 2 三角形的内角和
4.[2019·百色] 三角形的内角和等于( )
A.90° B.180° C.270° D.360°
5.在△ABC中,∠A+∠B=130°,则∠C的度数为 ( )
A.30° B.40° C.50° D.60°
6.如图三条直线两两相交于点A,B,C,CA⊥CB,∠1=30°,则∠2的度数为( )
A.50° B.60° C.70° D.80°
7.[2019·淮北期末] 如图在△ABC中,∠B=90°,MN∥AC,∠1=55°,则∠C的度数
是( )
A.25° B.35° C.45° D.55°
8.已知:如图则∠1= °,∠2= °,∠3= °.
9.在一个三角形中,三个内角的度数之比为1∶2∶6,则这个三角形的最大内角的度数是 .
10.(1)在△ABC中,若∠A=50°,∠B=∠C,求∠C的度数;
(2)在△ABC中,若∠A=80°,∠B-∠C=40°,求∠C的度数.
11.在△ABC中,已知∠A=∠B=∠C,判断△ABC的形状.
12.下面给出的四个三角形都有一部分被遮挡,其中不能确定三角形类型的是( )
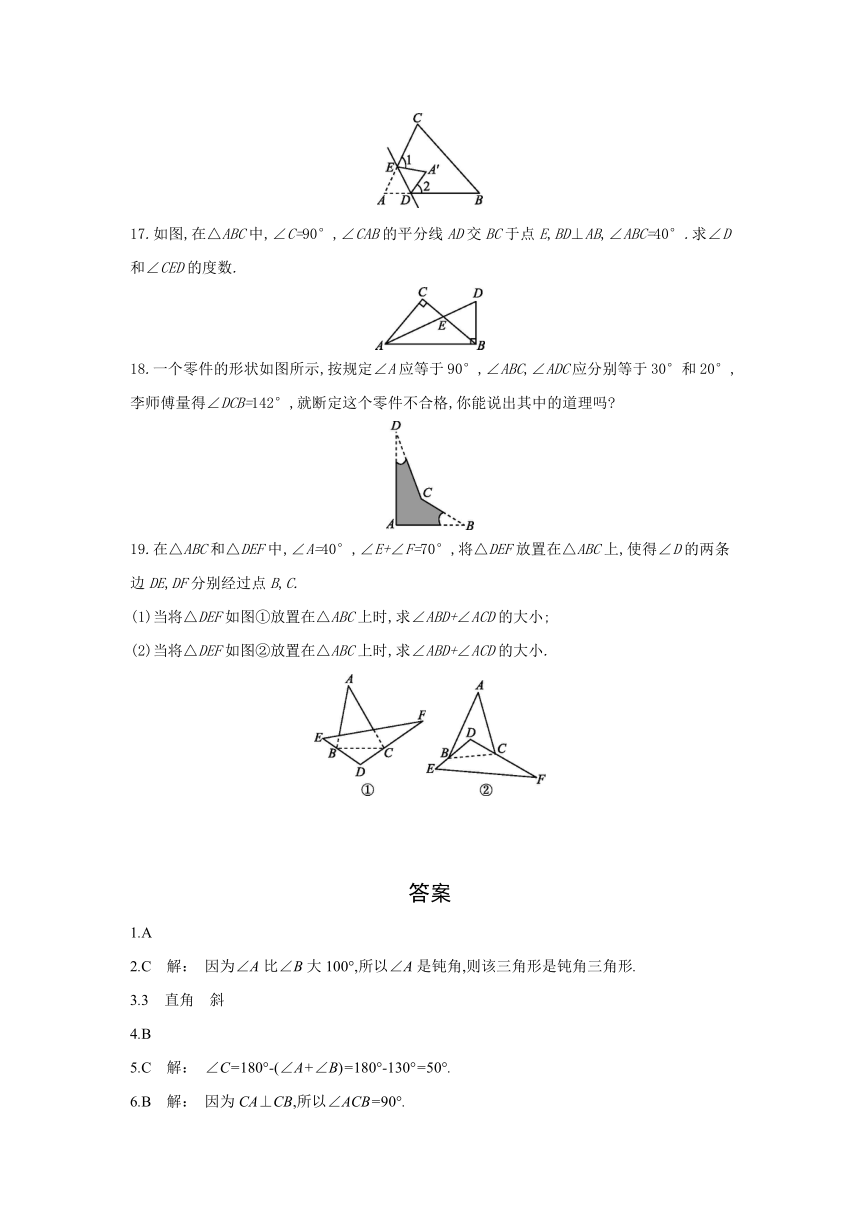
13.如图,在Rt△ABC中,∠ACB=90°,点D在AB边上,将△CBD沿CD折叠,使点B恰好落在AC边上的点E处.若∠A=26°,则∠CDE的度数是( )
A.71° B.64° C.80° D.45°
14.设三角形三个内角的度数分别为x°,y°,z°,如图果其中一个角的度数是另一个角的度数的2倍,那么我们称数对(y,z)(y≤z)是x的和谐数对,当x=150时,对应的和谐数对有一个,它为(10,20);当x=66时,对应的和谐数对有两个,它们为(33,81),(38,76).当对应的和谐数对(y,z)有三个时,请写出此时x的取值范围: .
15.[教材练习第3题变式题] 如图所示,在△ABC中,∠B=45°,∠BAC=85°,AD⊥BC,垂足为D,求∠CAD的度数.
16.如图,在折纸活动中,小李制作了一张△ABC的纸片,点D,E分别在边AB,AC上,将△ABC沿着DE折叠压平,点A与点A'重合.
(1)若∠B=50°,∠C=60°,求∠A的度数;
(2)若∠1+∠2=130°,求∠A的度数.
17.如图,在△ABC中,∠C=90°,∠CAB的平分线AD交BC于点E,BD⊥AB,∠ABC=40°.求∠D和∠CED的度数.
18.一个零件的形状如图所示,按规定∠A应等于90°,∠ABC,∠ADC应分别等于30°和20°,李师傅量得∠DCB=142°,就断定这个零件不合格,你能说出其中的道理吗
19.在△ABC和△DEF中,∠A=40°,∠E+∠F=70°,将△DEF放置在△ABC上,使得∠D的两条边DE,DF分别经过点B,C.
(1)当将△DEF如图①放置在△ABC上时,求∠ABD+∠ACD的大小;
(2)当将△DEF如图②放置在△ABC上时,求∠ABD+∠ACD的大小.
答案
1.A
2.C 解: 因为∠A比∠B大100°,所以∠A是钝角,则该三角形是钝角三角形.
3.3 直角 斜
4.B
5.C 解: ∠C=180°-(∠A+∠B)=180°-130°=50°.
6.B 解: 因为CA⊥CB,所以∠ACB=90°.
所以∠2=180°-∠ACB-∠1=180°-90°-30°=60°.故选B.
7.B 解: 因为∠B=90°,∠BMN=∠1=55°,
所以∠BNM=180°-90°-55°=35°.
因为MN∥AC,
所以∠C=∠BNM=35°.故选B.
8.60 35 90
9.120° 解: 设这个三角形的三个内角分别为x,2x,6x.由题意,得x+2x+6x=180°,解得x=20°,所以2x=40°,6x=120°,故这个三角形的最大内角的度数是120°.
10.解:(1)因为∠A=50°,∠B=∠C,
所以∠C==65°.
(2)由题意,得∠B+∠C=180°-∠A=100°.
又因为∠B-∠C=40°,所以∠C=30°.
11.解:因为∠A=∠B=∠C,
所以∠B=3∠A,∠C=5∠A.
因为∠A+∠B+∠C=180°,
所以∠A+3∠A+5∠A=180°,
所以∠A=20°,∠B=60°,∠C=100°,
所以△ABC是钝角三角形.
12.A 解: 观察象可知:选项B中的三角形是直角三角形,选项C中的三角形是锐角三角形,选项D中的三角形是钝角三角形,选项A中只能看出一个角是锐角,这样的三角形无法判断其类型.
13.A 解: 由折叠可得∠ACD=∠BCD,∠BDC=∠CDE.
因为∠ACB=90°,所以∠ACD=∠BCD=45°,∠B=90°-∠A=64°.
所以∠CDE=∠BDC=18BCD=71°.故选A.
14.0当0当x=45时,它的和谐数对有(22.5,112.5),(45,90);
当45当60≤x<120时,它的和谐数对有,180-,,;
当120≤x<180时,它的和谐数对有,.
故当对应的和谐数对(y,z)有三个时,此时x的取值范围是0故答案为015.解:在△ABC中,因为∠B=45°,∠BAC=85°,根据三角形内角和等于180°,得
∠C=180°-45°-85°=50°.
因为AD⊥BC,所以∠ADC=90°.
所以∠CAD=180°-90°-50°=40°.
16.解:(1)因为∠A+∠B+∠C=180°,
所以∠A=180°-(∠B+∠C)=180°-(50°+60°)=70°.
(2)由题意,得∠AED=∠A'ED,∠ADE=∠A'DE,∠A=∠A',
所以∠AED+∠ADE=∠A'ED+∠A'DE=180°-∠A,
所以∠1+∠2=360°-2(180°-∠A)=2∠A,
所以∠A=×130°=65°.
17.解:在△ABC中,∠C=90°,∠ABC=40°,
所以∠CAB=18ABC=180°-90°-40°=50°.
因为AD平分∠CAB,
所以∠BAD=∠CAB=×50°=25°.
在△ABE中,∠BAE=25°,∠ABE=40°,
所以∠AEB=180°-∠BAE-∠ABE=180°-25°-40°=115°,
所以∠CED=115°.
因为BD⊥AB,
所以∠ABD=90°.
在△ABD中,∠BAD=25°,∠ABD=90°,
所以∠D=180°-∠BAD-∠ABD=180°-25°-90°=65°.
18.解:连接BD.假设这个零件合格,则∠A=90°.
因为∠ABC=30°,∠ADC=20°,
所以∠A+∠ABC+∠ADC=90°+30°+20°=140°.
根据三角形的内角和等于180°,
得∠A+∠ADB+∠ABD=180°,
所以∠CDB+∠CBD=180°-140°=40°.
又因为∠DCB+∠CDB+∠CBD=180°,
所以∠DCB=180°-40°=140°.
这说明若零件合格,则∠DCB=140°,
而李师傅量得∠DCB=142°,
所以可以断定这个零件不合格.
19.解:(1)由题意可知∠D=180°-70°=110°.
所以∠DBC+∠DCB=180°-∠D=70°.
又因为∠ABC+∠ACB=180°-∠A=140°,
所以∠ABD+∠ACD=(∠ABC+∠DBC)+(∠ACB+∠DCB)=210°.
(2)因为在△ABC中,∠A=40°,
所以∠ABC+∠ACB=140°.
因为在△DEF中,∠E+∠F=70°,
所以∠D=110°,
所以∠BCD+∠CBD=180°-∠D=70°,
所以∠ABD+∠ACD=(∠ABC+∠ACB)-(∠BCD+∠CBD)=140°-70°=70 °.
知识点 1 三角形按角的大小分类
1.若一个三角形的三个内角的度数分别是80°,60°,40°,则这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
2.在△ABC中,∠A比∠B大100°,则△ABC的形状是( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.无法判断
3.如图示,中有 个直角三角形,其中BC是△ABC的 边,BC是△BCD的 边.
知识点 2 三角形的内角和
4.[2019·百色] 三角形的内角和等于( )
A.90° B.180° C.270° D.360°
5.在△ABC中,∠A+∠B=130°,则∠C的度数为 ( )
A.30° B.40° C.50° D.60°
6.如图三条直线两两相交于点A,B,C,CA⊥CB,∠1=30°,则∠2的度数为( )
A.50° B.60° C.70° D.80°
7.[2019·淮北期末] 如图在△ABC中,∠B=90°,MN∥AC,∠1=55°,则∠C的度数
是( )
A.25° B.35° C.45° D.55°
8.已知:如图则∠1= °,∠2= °,∠3= °.
9.在一个三角形中,三个内角的度数之比为1∶2∶6,则这个三角形的最大内角的度数是 .
10.(1)在△ABC中,若∠A=50°,∠B=∠C,求∠C的度数;
(2)在△ABC中,若∠A=80°,∠B-∠C=40°,求∠C的度数.
11.在△ABC中,已知∠A=∠B=∠C,判断△ABC的形状.
12.下面给出的四个三角形都有一部分被遮挡,其中不能确定三角形类型的是( )
13.如图,在Rt△ABC中,∠ACB=90°,点D在AB边上,将△CBD沿CD折叠,使点B恰好落在AC边上的点E处.若∠A=26°,则∠CDE的度数是( )
A.71° B.64° C.80° D.45°
14.设三角形三个内角的度数分别为x°,y°,z°,如图果其中一个角的度数是另一个角的度数的2倍,那么我们称数对(y,z)(y≤z)是x的和谐数对,当x=150时,对应的和谐数对有一个,它为(10,20);当x=66时,对应的和谐数对有两个,它们为(33,81),(38,76).当对应的和谐数对(y,z)有三个时,请写出此时x的取值范围: .
15.[教材练习第3题变式题] 如图所示,在△ABC中,∠B=45°,∠BAC=85°,AD⊥BC,垂足为D,求∠CAD的度数.
16.如图,在折纸活动中,小李制作了一张△ABC的纸片,点D,E分别在边AB,AC上,将△ABC沿着DE折叠压平,点A与点A'重合.
(1)若∠B=50°,∠C=60°,求∠A的度数;
(2)若∠1+∠2=130°,求∠A的度数.
17.如图,在△ABC中,∠C=90°,∠CAB的平分线AD交BC于点E,BD⊥AB,∠ABC=40°.求∠D和∠CED的度数.
18.一个零件的形状如图所示,按规定∠A应等于90°,∠ABC,∠ADC应分别等于30°和20°,李师傅量得∠DCB=142°,就断定这个零件不合格,你能说出其中的道理吗
19.在△ABC和△DEF中,∠A=40°,∠E+∠F=70°,将△DEF放置在△ABC上,使得∠D的两条边DE,DF分别经过点B,C.
(1)当将△DEF如图①放置在△ABC上时,求∠ABD+∠ACD的大小;
(2)当将△DEF如图②放置在△ABC上时,求∠ABD+∠ACD的大小.
答案
1.A
2.C 解: 因为∠A比∠B大100°,所以∠A是钝角,则该三角形是钝角三角形.
3.3 直角 斜
4.B
5.C 解: ∠C=180°-(∠A+∠B)=180°-130°=50°.
6.B 解: 因为CA⊥CB,所以∠ACB=90°.
所以∠2=180°-∠ACB-∠1=180°-90°-30°=60°.故选B.
7.B 解: 因为∠B=90°,∠BMN=∠1=55°,
所以∠BNM=180°-90°-55°=35°.
因为MN∥AC,
所以∠C=∠BNM=35°.故选B.
8.60 35 90
9.120° 解: 设这个三角形的三个内角分别为x,2x,6x.由题意,得x+2x+6x=180°,解得x=20°,所以2x=40°,6x=120°,故这个三角形的最大内角的度数是120°.
10.解:(1)因为∠A=50°,∠B=∠C,
所以∠C==65°.
(2)由题意,得∠B+∠C=180°-∠A=100°.
又因为∠B-∠C=40°,所以∠C=30°.
11.解:因为∠A=∠B=∠C,
所以∠B=3∠A,∠C=5∠A.
因为∠A+∠B+∠C=180°,
所以∠A+3∠A+5∠A=180°,
所以∠A=20°,∠B=60°,∠C=100°,
所以△ABC是钝角三角形.
12.A 解: 观察象可知:选项B中的三角形是直角三角形,选项C中的三角形是锐角三角形,选项D中的三角形是钝角三角形,选项A中只能看出一个角是锐角,这样的三角形无法判断其类型.
13.A 解: 由折叠可得∠ACD=∠BCD,∠BDC=∠CDE.
因为∠ACB=90°,所以∠ACD=∠BCD=45°,∠B=90°-∠A=64°.
所以∠CDE=∠BDC=18BCD=71°.故选A.
14.0
当45
当120≤x<180时,它的和谐数对有,.
故当对应的和谐数对(y,z)有三个时,此时x的取值范围是0
∠C=180°-45°-85°=50°.
因为AD⊥BC,所以∠ADC=90°.
所以∠CAD=180°-90°-50°=40°.
16.解:(1)因为∠A+∠B+∠C=180°,
所以∠A=180°-(∠B+∠C)=180°-(50°+60°)=70°.
(2)由题意,得∠AED=∠A'ED,∠ADE=∠A'DE,∠A=∠A',
所以∠AED+∠ADE=∠A'ED+∠A'DE=180°-∠A,
所以∠1+∠2=360°-2(180°-∠A)=2∠A,
所以∠A=×130°=65°.
17.解:在△ABC中,∠C=90°,∠ABC=40°,
所以∠CAB=18ABC=180°-90°-40°=50°.
因为AD平分∠CAB,
所以∠BAD=∠CAB=×50°=25°.
在△ABE中,∠BAE=25°,∠ABE=40°,
所以∠AEB=180°-∠BAE-∠ABE=180°-25°-40°=115°,
所以∠CED=115°.
因为BD⊥AB,
所以∠ABD=90°.
在△ABD中,∠BAD=25°,∠ABD=90°,
所以∠D=180°-∠BAD-∠ABD=180°-25°-90°=65°.
18.解:连接BD.假设这个零件合格,则∠A=90°.
因为∠ABC=30°,∠ADC=20°,
所以∠A+∠ABC+∠ADC=90°+30°+20°=140°.
根据三角形的内角和等于180°,
得∠A+∠ADB+∠ABD=180°,
所以∠CDB+∠CBD=180°-140°=40°.
又因为∠DCB+∠CDB+∠CBD=180°,
所以∠DCB=180°-40°=140°.
这说明若零件合格,则∠DCB=140°,
而李师傅量得∠DCB=142°,
所以可以断定这个零件不合格.
19.解:(1)由题意可知∠D=180°-70°=110°.
所以∠DBC+∠DCB=180°-∠D=70°.
又因为∠ABC+∠ACB=180°-∠A=140°,
所以∠ABD+∠ACD=(∠ABC+∠DBC)+(∠ACB+∠DCB)=210°.
(2)因为在△ABC中,∠A=40°,
所以∠ABC+∠ACB=140°.
因为在△DEF中,∠E+∠F=70°,
所以∠D=110°,
所以∠BCD+∠CBD=180°-∠D=70°,
所以∠ABD+∠ACD=(∠ABC+∠ACB)-(∠BCD+∠CBD)=140°-70°=70 °.
