沪科版数学八年级上册 14.1 全等三角形 同步课时练习(word版含答案)
文档属性
| 名称 | 沪科版数学八年级上册 14.1 全等三角形 同步课时练习(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 243.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 17:06:17 | ||
图片预览

文档简介
14.1 全等三角形
知识点 1 全等形及全等三角形
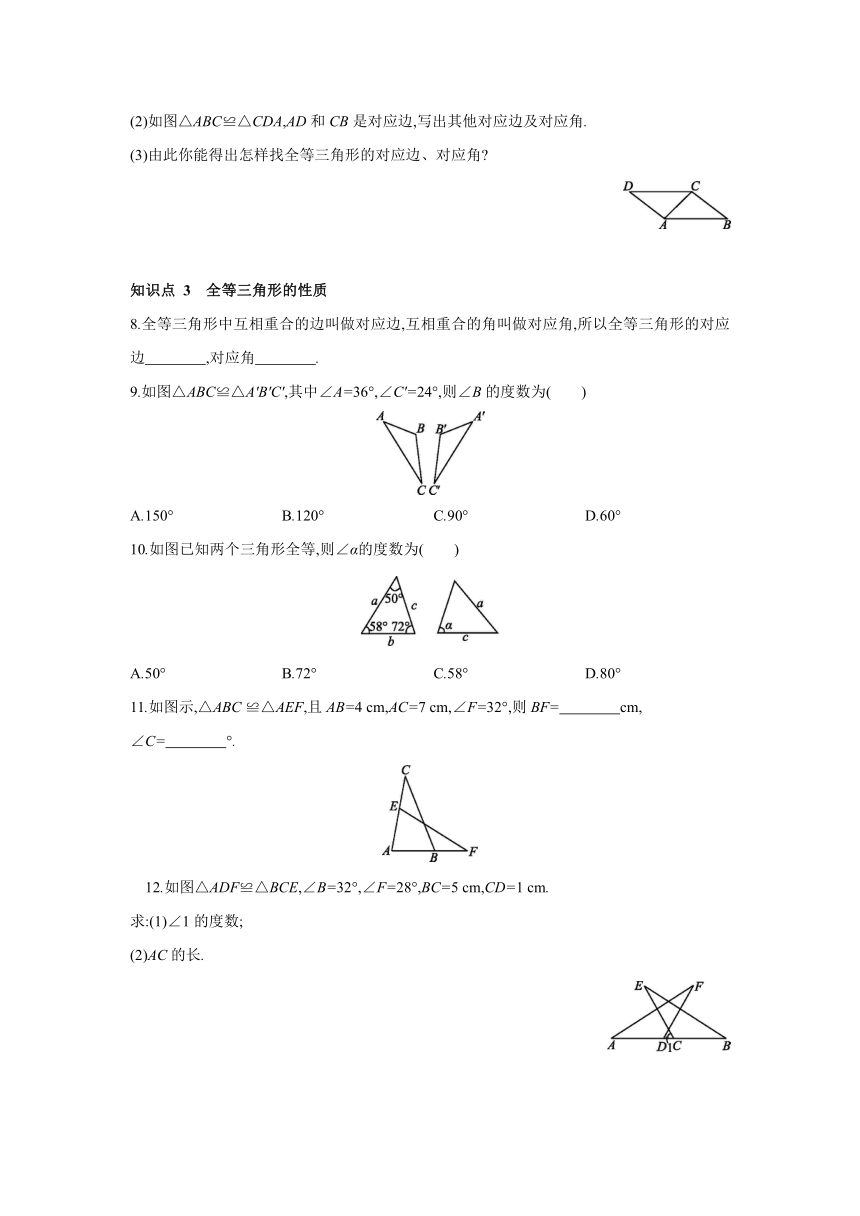
1.请将下列形中通过变换后能够完全重合的连接起来.
2.有下列命题:①形状相同的形是全等形;②能够完全重合的两个三角形全等;③经过平移得到的形与原形是全等形.其中真命题有( )
A.0个 B.1个 C.2个 D.3个
3.由同一张底片冲洗出来的两张五寸照片中的案 全等形;由同一张底片冲洗出来的五寸照片和七寸照片中的案 全等形.(填“是”或“不是”)
知识点 2 全等三角形的对应元素
4.如图示,沿直线AC对折,△ABC与△ADC重合,则△ABC≌ ,AB的对应边是 ,AC的对应边是 ,∠BCA的对应角是 .
5.如图△ABC≌△DEF,且∠ACB与∠F是一组对应角,AB与DE是一组对应边,下面与BC是对应边的是( )
A.AC B.CE C.EF D.DF
6.如图△ABC≌△ADE,∠B与∠D是对应角,AB与AD是对应边,另外两组对应边为 ,对应角为 .
7.[教材练习第2题变式题] (1)△AEC≌△ADB,点E和点D是对应顶点,写出它们的对应边和对应角;
(2)如图△ABC≌△CDA,AD和CB是对应边,写出其他对应边及对应角.
(3)由此你能得出怎样找全等三角形的对应边、对应角
知识点 3 全等三角形的性质
8.全等三角形中互相重合的边叫做对应边,互相重合的角叫做对应角,所以全等三角形的对应边 ,对应角 .
9.如图△ABC≌△A'B'C',其中∠A=36°,∠C'=24°,则∠B的度数为( )
A.150° B.120° C.90° D.60°
10.如图已知两个三角形全等,则∠α的度数为( )
A.50° B.72° C.58° D.80°
11.如图示,△ABC ≌△AEF,且AB=4 cm,AC=7 cm,∠F=32°,则BF= cm,
∠C= °.
12.如图△ADF≌△BCE,∠B=32°,∠F=28°,BC=5 cm,CD=1 cm.
求:(1)∠1的度数;
(2)AC的长.
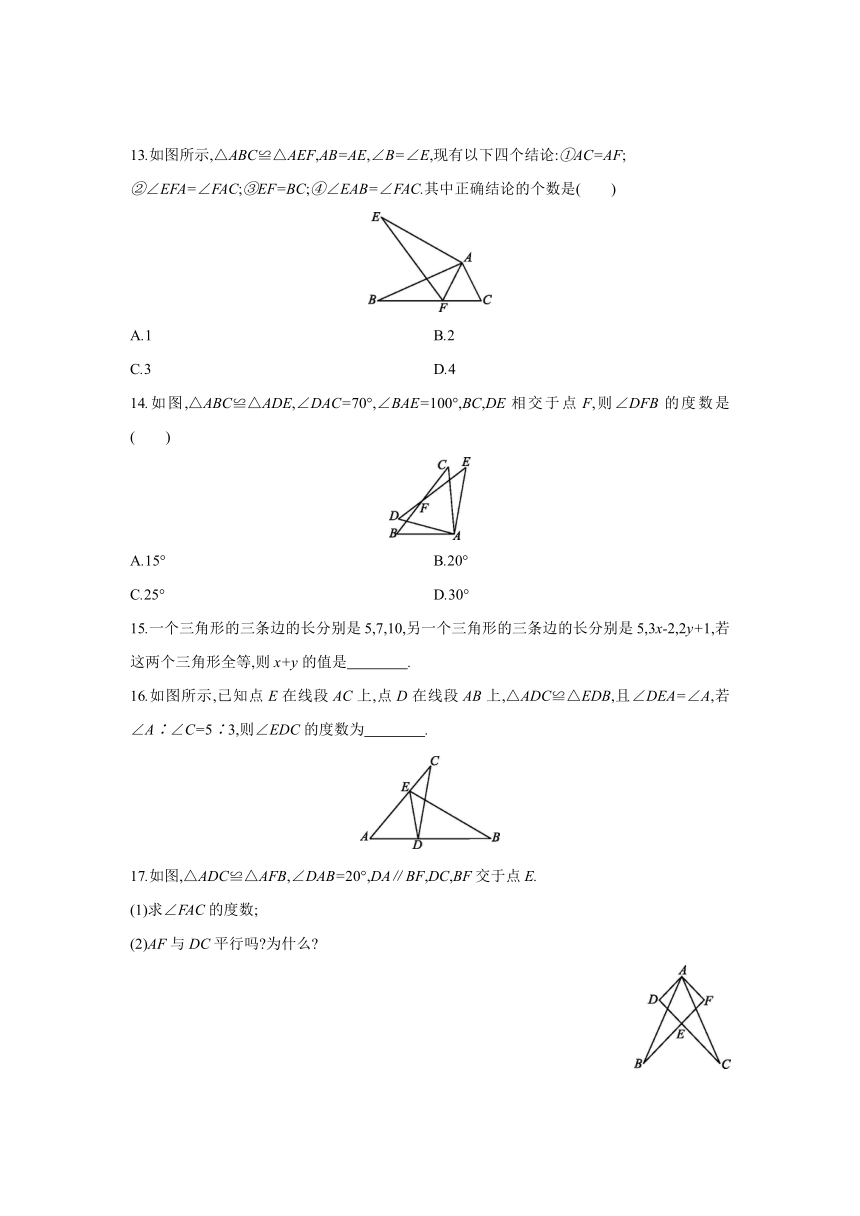
13.如图所示,△ABC≌△AEF,AB=AE,∠B=∠E,现有以下四个结论:①AC=AF;
②∠EFA=∠FAC;③EF=BC;④∠EAB=∠FAC.其中正确结论的个数是( )
A.1 B.2
C.3 D.4
14.如图,△ABC≌△ADE,∠DAC=70°,∠BAE=100°,BC,DE相交于点F,则∠DFB的度数是( )
A.15° B.20°
C.25° D.30°
15.一个三角形的三条边的长分别是5,7,10,另一个三角形的三条边的长分别是5,3x-2,2y+1,若这两个三角形全等,则x+y的值是 .
16.如图所示,已知点E在线段AC上,点D在线段AB上,△ADC≌△EDB,且∠DEA=∠A,若∠A∶∠C=5∶3,则∠EDC的度数为 .
17.如图,△ADC≌△AFB,∠DAB=20°,DA∥BF,DC,BF交于点E.
(1)求∠FAC的度数;
(2)AF与DC平行吗 为什么
18.如图,A,D,E三点在同一直线上,且△BAD≌△ACE.
(1)你能说明BD,DE,CE之间的数量关系吗
(2)当△ABD满足什么条件时,BD∥CE
答案
1.解:如图所示.
2.C
3.是 不是 解: 全等形要保证形的形状相同、大小相等.
4.△ADC AD AC ∠DCA 5.C
6.AC与AE,BC与DE ∠C与∠E,∠BAC与∠DAE
7.解:(1)∵△AEC≌△ADB,点E和点D是对应顶点,
∴AC的对应边是AB,EC的对应边是DB,AE的对应边是AD,∠EAC的对应角是∠DAB,∠AEC的对应角是∠ADB,∠ECA的对应角是∠DBA.
(2)∵△ABC≌△CDA,AD和CB是对应边,
∴其他对应边:AC与CA,AB与CD;
对应角:∠B与∠D,∠BAC与∠DCA,∠ACB与∠CAD.
(3)可以根据全等三角形的书写方式,根据对应顶点写在对应位置,可以找出对应边、对应角.还有公共边是对应边,公共角是对应角,对顶角是对应角,最大的边对最大的边,最短的边对最短的边,最大的角对最大的角,最小的角对最小的角,对应边所对的角是对应角.
8.相等 相等
9.B 解: ∵△ABC≌△A'B'C',∴∠C=∠C'=24°.又∵∠A=36°,∴∠B=180°-24°-36°=120°.
10.B
11.3 32 解: 利用全等三角形的对应边相等,对应角相等,可知AC=AF=7 cm,∠C=
∠F=32°,∴BF=7-4=3(cm).
12.解:(1)∵△ADF≌△BCE,∠F=28°,
∴∠E=∠F=28°,
∴∠1=∠B+∠E=32°+28°=60°.
(2)∵△ADF≌△BCE,BC=5 cm,
∴AD=BC=5 cm.
又∵CD=1 cm,∴AC=AD+CD=6(cm).
13.C 解: 在本题中,∠B和∠E是对应角,那么它们所对的边AC和AF就是对应边,因此AC与AF一定相等.故①是正确的.又因为AB与AE,AF与AC都是对应边,所以EF与BC也是对应边.所以③也是正确的.而它们的对角∠EAF与∠BAC为对应角,所以∠EAF=∠BAC.因此∠EAB=∠FAC(在∠EAF=∠BAC的两边同时减去∠BAF,可得∠EAB=∠FAC).故④也是正确的.而②中∠EFA不一定与∠FAC相等.
14.A 解: ∵△ABC≌△ADE,∴∠B=∠D,∠BAC=∠DAE.又∵∠BAD=∠BAC-∠CAD,
∠CAE=∠DAE-∠CAD,∴∠BAD=∠CAE.∵∠DAC=70°,∠BAE=100°,∴∠BAD=(∠BAE-
∠DAC)=(100°-70°)=15°.设BC与AD相交于点G.在△ABG和△FDG中,∵∠B=∠D,∠AGB=∠FGD,∴∠DFB=∠BAD=15°.故选A.
15.或7 解: 根据全等三角形的性质,可知分两种情况:①②
解方程组求出x+y的值即可.
16.20 ° 解: ∵∠A∶∠C=5∶3,∴令∠A=5x,∠C=3x,则∠CDB=∠A+∠C=5x+3x=8x.
∵△ADC≌△EDB,(已知)
∴∠ADC=∠EDB,(全等三角形的对应角相等)
∴∠ADC-∠EDC=∠EDB-∠EDC,
即∠ADE=∠CDB=8x.
∵∠DEA=∠A,∴∠DEA=5x.
在△ADE中,∠A+∠ADE+∠DEA=180°,
即5x+8x+5x=180°.
∴x=10°.
而∠DEA=∠C+∠EDC,
∴∠EDC=∠DEA-∠C=5x-3x=2x,
∴∠EDC=2x=20°.
17.解:(1)∵△ADC≌△AFB,∴∠DAC=∠FAB.
∴∠DAC-∠BAC=∠FAB-∠BAC,
即∠DAB=∠FAC.∴∠FAC=20°.
(2)平行.理由:∵DA∥BF,
∴∠DAF+∠F=180°.
∵△ADC≌△AFB,∴∠D=∠F.
∴∠DAF+∠D=180°.∴AF∥DC.
18.解:(1)BD=DE+CE.
理由:∵△BAD≌△ACE,
∴BD=AE,AD=CE,
∴BD=AE=AD+DE=CE+DE,
即BD=DE+CE.
(2)△ABD满足∠ADB=90°时,BD∥CE.
理由:∵△BAD≌△ACE,
∴∠E=∠ADB=90°(添加的条件是∠ADB=90°),
∴∠BDE=180°-90°=90°=∠E,
∴BD∥CE.
知识点 1 全等形及全等三角形
1.请将下列形中通过变换后能够完全重合的连接起来.
2.有下列命题:①形状相同的形是全等形;②能够完全重合的两个三角形全等;③经过平移得到的形与原形是全等形.其中真命题有( )
A.0个 B.1个 C.2个 D.3个
3.由同一张底片冲洗出来的两张五寸照片中的案 全等形;由同一张底片冲洗出来的五寸照片和七寸照片中的案 全等形.(填“是”或“不是”)
知识点 2 全等三角形的对应元素
4.如图示,沿直线AC对折,△ABC与△ADC重合,则△ABC≌ ,AB的对应边是 ,AC的对应边是 ,∠BCA的对应角是 .
5.如图△ABC≌△DEF,且∠ACB与∠F是一组对应角,AB与DE是一组对应边,下面与BC是对应边的是( )
A.AC B.CE C.EF D.DF
6.如图△ABC≌△ADE,∠B与∠D是对应角,AB与AD是对应边,另外两组对应边为 ,对应角为 .
7.[教材练习第2题变式题] (1)△AEC≌△ADB,点E和点D是对应顶点,写出它们的对应边和对应角;
(2)如图△ABC≌△CDA,AD和CB是对应边,写出其他对应边及对应角.
(3)由此你能得出怎样找全等三角形的对应边、对应角
知识点 3 全等三角形的性质
8.全等三角形中互相重合的边叫做对应边,互相重合的角叫做对应角,所以全等三角形的对应边 ,对应角 .
9.如图△ABC≌△A'B'C',其中∠A=36°,∠C'=24°,则∠B的度数为( )
A.150° B.120° C.90° D.60°
10.如图已知两个三角形全等,则∠α的度数为( )
A.50° B.72° C.58° D.80°
11.如图示,△ABC ≌△AEF,且AB=4 cm,AC=7 cm,∠F=32°,则BF= cm,
∠C= °.
12.如图△ADF≌△BCE,∠B=32°,∠F=28°,BC=5 cm,CD=1 cm.
求:(1)∠1的度数;
(2)AC的长.
13.如图所示,△ABC≌△AEF,AB=AE,∠B=∠E,现有以下四个结论:①AC=AF;
②∠EFA=∠FAC;③EF=BC;④∠EAB=∠FAC.其中正确结论的个数是( )
A.1 B.2
C.3 D.4
14.如图,△ABC≌△ADE,∠DAC=70°,∠BAE=100°,BC,DE相交于点F,则∠DFB的度数是( )
A.15° B.20°
C.25° D.30°
15.一个三角形的三条边的长分别是5,7,10,另一个三角形的三条边的长分别是5,3x-2,2y+1,若这两个三角形全等,则x+y的值是 .
16.如图所示,已知点E在线段AC上,点D在线段AB上,△ADC≌△EDB,且∠DEA=∠A,若∠A∶∠C=5∶3,则∠EDC的度数为 .
17.如图,△ADC≌△AFB,∠DAB=20°,DA∥BF,DC,BF交于点E.
(1)求∠FAC的度数;
(2)AF与DC平行吗 为什么
18.如图,A,D,E三点在同一直线上,且△BAD≌△ACE.
(1)你能说明BD,DE,CE之间的数量关系吗
(2)当△ABD满足什么条件时,BD∥CE
答案
1.解:如图所示.
2.C
3.是 不是 解: 全等形要保证形的形状相同、大小相等.
4.△ADC AD AC ∠DCA 5.C
6.AC与AE,BC与DE ∠C与∠E,∠BAC与∠DAE
7.解:(1)∵△AEC≌△ADB,点E和点D是对应顶点,
∴AC的对应边是AB,EC的对应边是DB,AE的对应边是AD,∠EAC的对应角是∠DAB,∠AEC的对应角是∠ADB,∠ECA的对应角是∠DBA.
(2)∵△ABC≌△CDA,AD和CB是对应边,
∴其他对应边:AC与CA,AB与CD;
对应角:∠B与∠D,∠BAC与∠DCA,∠ACB与∠CAD.
(3)可以根据全等三角形的书写方式,根据对应顶点写在对应位置,可以找出对应边、对应角.还有公共边是对应边,公共角是对应角,对顶角是对应角,最大的边对最大的边,最短的边对最短的边,最大的角对最大的角,最小的角对最小的角,对应边所对的角是对应角.
8.相等 相等
9.B 解: ∵△ABC≌△A'B'C',∴∠C=∠C'=24°.又∵∠A=36°,∴∠B=180°-24°-36°=120°.
10.B
11.3 32 解: 利用全等三角形的对应边相等,对应角相等,可知AC=AF=7 cm,∠C=
∠F=32°,∴BF=7-4=3(cm).
12.解:(1)∵△ADF≌△BCE,∠F=28°,
∴∠E=∠F=28°,
∴∠1=∠B+∠E=32°+28°=60°.
(2)∵△ADF≌△BCE,BC=5 cm,
∴AD=BC=5 cm.
又∵CD=1 cm,∴AC=AD+CD=6(cm).
13.C 解: 在本题中,∠B和∠E是对应角,那么它们所对的边AC和AF就是对应边,因此AC与AF一定相等.故①是正确的.又因为AB与AE,AF与AC都是对应边,所以EF与BC也是对应边.所以③也是正确的.而它们的对角∠EAF与∠BAC为对应角,所以∠EAF=∠BAC.因此∠EAB=∠FAC(在∠EAF=∠BAC的两边同时减去∠BAF,可得∠EAB=∠FAC).故④也是正确的.而②中∠EFA不一定与∠FAC相等.
14.A 解: ∵△ABC≌△ADE,∴∠B=∠D,∠BAC=∠DAE.又∵∠BAD=∠BAC-∠CAD,
∠CAE=∠DAE-∠CAD,∴∠BAD=∠CAE.∵∠DAC=70°,∠BAE=100°,∴∠BAD=(∠BAE-
∠DAC)=(100°-70°)=15°.设BC与AD相交于点G.在△ABG和△FDG中,∵∠B=∠D,∠AGB=∠FGD,∴∠DFB=∠BAD=15°.故选A.
15.或7 解: 根据全等三角形的性质,可知分两种情况:①②
解方程组求出x+y的值即可.
16.20 ° 解: ∵∠A∶∠C=5∶3,∴令∠A=5x,∠C=3x,则∠CDB=∠A+∠C=5x+3x=8x.
∵△ADC≌△EDB,(已知)
∴∠ADC=∠EDB,(全等三角形的对应角相等)
∴∠ADC-∠EDC=∠EDB-∠EDC,
即∠ADE=∠CDB=8x.
∵∠DEA=∠A,∴∠DEA=5x.
在△ADE中,∠A+∠ADE+∠DEA=180°,
即5x+8x+5x=180°.
∴x=10°.
而∠DEA=∠C+∠EDC,
∴∠EDC=∠DEA-∠C=5x-3x=2x,
∴∠EDC=2x=20°.
17.解:(1)∵△ADC≌△AFB,∴∠DAC=∠FAB.
∴∠DAC-∠BAC=∠FAB-∠BAC,
即∠DAB=∠FAC.∴∠FAC=20°.
(2)平行.理由:∵DA∥BF,
∴∠DAF+∠F=180°.
∵△ADC≌△AFB,∴∠D=∠F.
∴∠DAF+∠D=180°.∴AF∥DC.
18.解:(1)BD=DE+CE.
理由:∵△BAD≌△ACE,
∴BD=AE,AD=CE,
∴BD=AE=AD+DE=CE+DE,
即BD=DE+CE.
(2)△ABD满足∠ADB=90°时,BD∥CE.
理由:∵△BAD≌△ACE,
∴∠E=∠ADB=90°(添加的条件是∠ADB=90°),
∴∠BDE=180°-90°=90°=∠E,
∴BD∥CE.
