人教版 七年级下册 列方程(组)和不等式(组)解决实际问题 复习课件(共18张PPT)
文档属性
| 名称 | 人教版 七年级下册 列方程(组)和不等式(组)解决实际问题 复习课件(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 8.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 18:05:09 | ||
图片预览




文档简介
(共18张PPT)
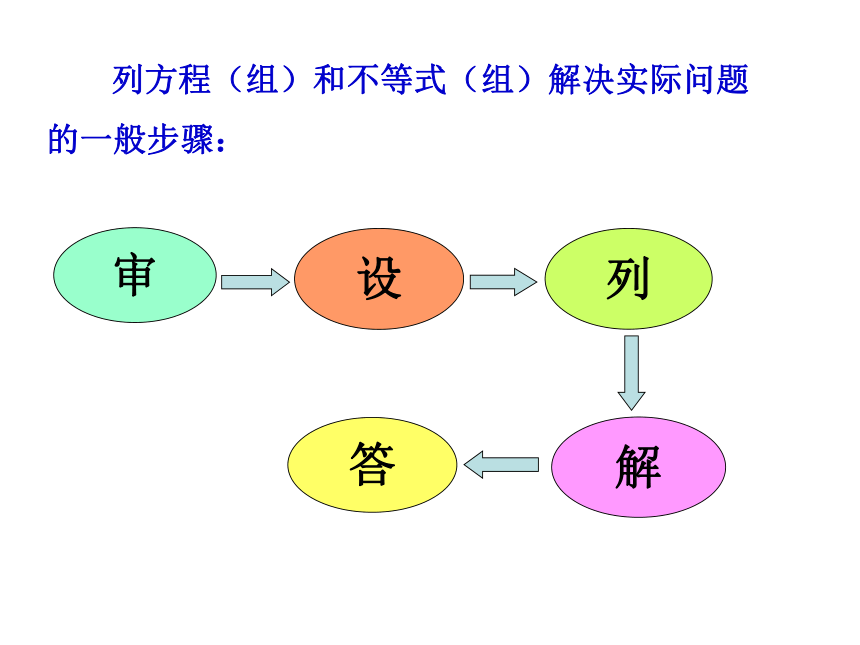
列方程(组)和不等式(组)解决实际问题
的一般步骤:
审
设
列
解
答
例题 &分析
pc
为了抓住我市今年夏季文化节的商机,大连商场决定购进甲、乙两种纪念品,若购进甲种纪念品 1 件,乙种纪念品 2 件,需要 160 元;购进甲种纪念品 2 件,乙种纪念品 3 件,需要 280元.
(1)求购进甲、乙两种纪念品每件各需要多少元?
例 1
(2)若该商场决定购进甲、乙两种纪念品 100 件,其中甲纪念品的进货量不少于 30 件,并且考虑市场需求和资金周转,用于购买这些纪念品的资金不能超过 5400 元,你认为该商场共有几种进货方案?
甲纪念品数量(件) 1 2
乙纪念品数量(件) 2 3
总费用(元) 160 280
例题 &分析
pc
为了抓住我市今年夏季文化节的商机,大连商场决定购进甲、乙两种纪念品,若购进甲种纪念品 1 件,乙种纪念品 2 件,需要 160 元;购进甲种纪念品 2 件,乙种纪念品 3 件,需要 280元.
例 1
(3)若该商场同时购进甲种纪念品 a 件,乙种纪念品 b 件,共花费 4000 元,其中甲种纪念品不少于 45 件,请你帮该商场设计进货方案.
例题 &分析
为了抓住我市今年夏季文化节的商机,大连商场决定购进甲、乙两种纪念品,若购进甲种纪念品 1 件,乙种纪念品 2 件,需要 160 元;购进甲种纪念品 2 件,乙种纪念品 3 件,需要 280元.
例 1
(4)在(2)的条件下,若销售每件甲种纪念品可获利 30元,每件乙种纪念品可获利 12 元,
若商家保持两种纪念品的售价不变,请你根据以上信息,设计出使这100件纪念品销售总利润最大的进货方案.
① 你认为哪种方案获利最大?最大利润是多少?
反馈 &训练
pa
pc
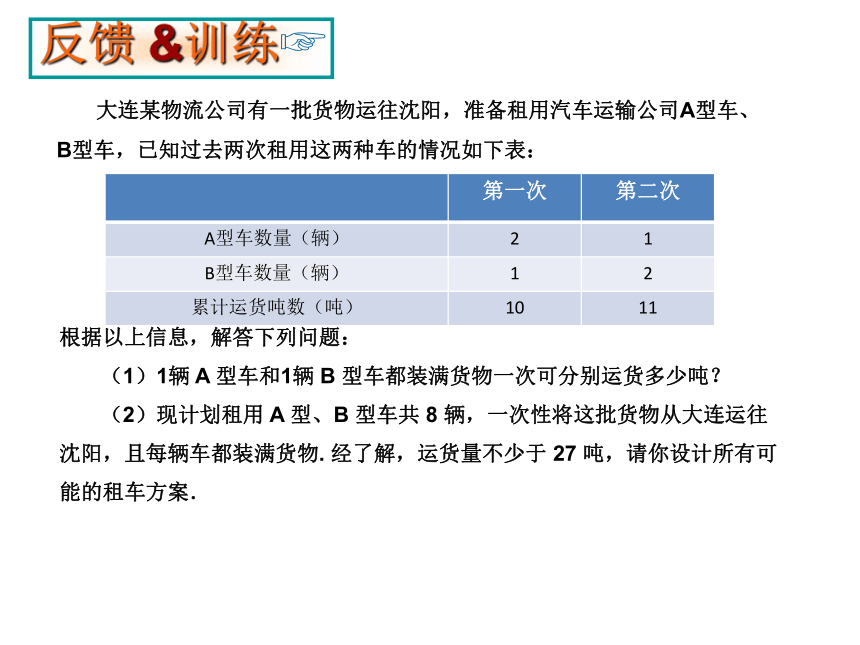
大连某物流公司有一批货物运往沈阳,准备租用汽车运输公司A型车、B型车,已知过去两次租用这两种车的情况如下表:
根据以上信息,解答下列问题:
(1)1辆 A 型车和1辆 B 型车都装满货物一次可分别运货多少吨?
(2)现计划租用 A 型、B 型车共 8 辆,一次性将这批货物从大连运往 沈阳,且每辆车都装满货物. 经了解,运货量不少于 27 吨,请你设计所有可能的租车方案.
第一次 第二次
A型车数量(辆) 2 1
B型车数量(辆) 1 2
累计运货吨数(吨) 10 11
反馈 &训练
pa
pc
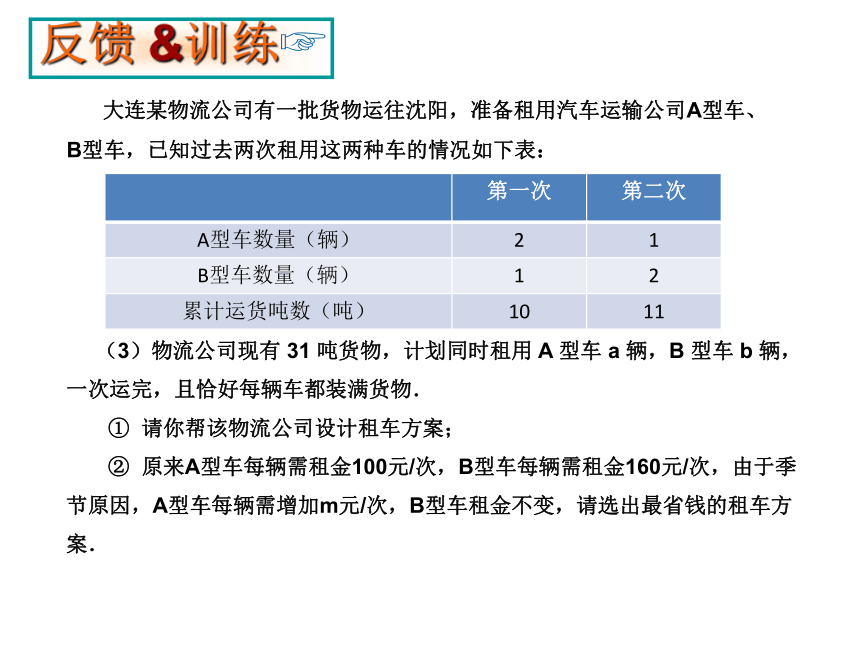
大连某物流公司有一批货物运往沈阳,准备租用汽车运输公司A型车、B型车,已知过去两次租用这两种车的情况如下表:
(3)物流公司现有 31 吨货物,计划同时租用 A 型车 a 辆,B 型车 b 辆, 一次运完,且恰好每辆车都装满货物.
① 请你帮该物流公司设计租车方案;
② 原来A型车每辆需租金100元/次,B型车每辆需租金160元/次,由于季节原因,A型车每辆需增加m元/次,B型车租金不变,请选出最省钱的租车方案.
第一次 第二次
A型车数量(辆) 2 1
B型车数量(辆) 1 2
累计运货吨数(吨) 10 11
本节课你都学到了什么
学案卷:课后作业、当堂检测
知识像一艘船,让它载着我们驶向理想的彼岸……
例题 &分析
pa
获利
例题 &分析
pa
逐个计算
比较大小
函数思想
文字叙述
3
种
方
法
甲 30
方案一:30×30+12×70=1740 元
方案二:30×31+12×69=1758元
方案三:30×32+12×68=1776元
方案四:30×33+12×67=1794元
方案五:30×34+12×66=1812元
方案六:30×35+12×65=1830元
>乙12
例题 &分析
pa
pc
每件甲纪念品利润(30 - m)元
分类讨论
例题 &分析
pa
(3)若该商场同时购进甲种纪念品 a 件,乙种纪念品 b 件,共花费 4000 元,其中甲种纪念品不少于45件,请你帮该商场设计进货方案.
解:由题意得:
∴ 商场共有 5 种进货方案.
∵
例题 &分析
pa
pc
(4)在(2)的条件下,若销售每件甲种纪念品可获利 30元,每件乙种纪念品可获利 12 元,
① 你认为哪种方案获利最大?最大利润是多少?
方法一:逐个计算,比较大小
解: 方案一的利润为:30×30+12×70=1740 元;
方案二的利润为:30×31+12×69=1758元;
方案三的利润为:30×32+12×68=1776元;
方案四的利润为:30×33+12×67=1794元;
方案五的利润为:30×34+12×66=1812元;
方案六的利润为:30×35+12×65=1830元.
∴ 方案六即购甲纪念品35件,购乙纪念品65件时获利最大,
最大利润为1830元.
∵
例题 &分析
方法二 :
即购甲纪念品 35 件,购乙纪念品 65 件时获利最大,
且最大利润为 18×35+1200 = 1830 元.
设商场销售利润为 w 元,根据题意可知:
∵ 18 > 0
函数思想
方法三:
∴ 购买甲纪念品越多,利润越大,
即购甲纪念品 35 件,购乙纪念品 65 件时获利最大.
最大利润为 30×35+12×65 = 1830元.
∵ 30 >12
例题 &分析
pa
pc
若商家保持两种纪念品的售价不变,请你根据以上信息,设计出使这100件纪念品销售总利润最大的进货方案.
(4)在(2)的条件下,若销售每件甲种纪念品可获利 30元,每件乙种纪念品可获利 12 元,
设商场销售总利润为 w 元 .
分类讨论
解:由题意可知 ,销售每件甲种纪念品可获利(30 - m)元 .
列方程(组)和不等式(组)解决实际问题
的一般步骤:
审
设
列
解
答
例题 &分析
pc
为了抓住我市今年夏季文化节的商机,大连商场决定购进甲、乙两种纪念品,若购进甲种纪念品 1 件,乙种纪念品 2 件,需要 160 元;购进甲种纪念品 2 件,乙种纪念品 3 件,需要 280元.
(1)求购进甲、乙两种纪念品每件各需要多少元?
例 1
(2)若该商场决定购进甲、乙两种纪念品 100 件,其中甲纪念品的进货量不少于 30 件,并且考虑市场需求和资金周转,用于购买这些纪念品的资金不能超过 5400 元,你认为该商场共有几种进货方案?
甲纪念品数量(件) 1 2
乙纪念品数量(件) 2 3
总费用(元) 160 280
例题 &分析
pc
为了抓住我市今年夏季文化节的商机,大连商场决定购进甲、乙两种纪念品,若购进甲种纪念品 1 件,乙种纪念品 2 件,需要 160 元;购进甲种纪念品 2 件,乙种纪念品 3 件,需要 280元.
例 1
(3)若该商场同时购进甲种纪念品 a 件,乙种纪念品 b 件,共花费 4000 元,其中甲种纪念品不少于 45 件,请你帮该商场设计进货方案.
例题 &分析
为了抓住我市今年夏季文化节的商机,大连商场决定购进甲、乙两种纪念品,若购进甲种纪念品 1 件,乙种纪念品 2 件,需要 160 元;购进甲种纪念品 2 件,乙种纪念品 3 件,需要 280元.
例 1
(4)在(2)的条件下,若销售每件甲种纪念品可获利 30元,每件乙种纪念品可获利 12 元,
若商家保持两种纪念品的售价不变,请你根据以上信息,设计出使这100件纪念品销售总利润最大的进货方案.
① 你认为哪种方案获利最大?最大利润是多少?
反馈 &训练
pa
pc
大连某物流公司有一批货物运往沈阳,准备租用汽车运输公司A型车、B型车,已知过去两次租用这两种车的情况如下表:
根据以上信息,解答下列问题:
(1)1辆 A 型车和1辆 B 型车都装满货物一次可分别运货多少吨?
(2)现计划租用 A 型、B 型车共 8 辆,一次性将这批货物从大连运往 沈阳,且每辆车都装满货物. 经了解,运货量不少于 27 吨,请你设计所有可能的租车方案.
第一次 第二次
A型车数量(辆) 2 1
B型车数量(辆) 1 2
累计运货吨数(吨) 10 11
反馈 &训练
pa
pc
大连某物流公司有一批货物运往沈阳,准备租用汽车运输公司A型车、B型车,已知过去两次租用这两种车的情况如下表:
(3)物流公司现有 31 吨货物,计划同时租用 A 型车 a 辆,B 型车 b 辆, 一次运完,且恰好每辆车都装满货物.
① 请你帮该物流公司设计租车方案;
② 原来A型车每辆需租金100元/次,B型车每辆需租金160元/次,由于季节原因,A型车每辆需增加m元/次,B型车租金不变,请选出最省钱的租车方案.
第一次 第二次
A型车数量(辆) 2 1
B型车数量(辆) 1 2
累计运货吨数(吨) 10 11
本节课你都学到了什么
学案卷:课后作业、当堂检测
知识像一艘船,让它载着我们驶向理想的彼岸……
例题 &分析
pa
获利
例题 &分析
pa
逐个计算
比较大小
函数思想
文字叙述
3
种
方
法
甲 30
方案一:30×30+12×70=1740 元
方案二:30×31+12×69=1758元
方案三:30×32+12×68=1776元
方案四:30×33+12×67=1794元
方案五:30×34+12×66=1812元
方案六:30×35+12×65=1830元
>乙12
例题 &分析
pa
pc
每件甲纪念品利润(30 - m)元
分类讨论
例题 &分析
pa
(3)若该商场同时购进甲种纪念品 a 件,乙种纪念品 b 件,共花费 4000 元,其中甲种纪念品不少于45件,请你帮该商场设计进货方案.
解:由题意得:
∴ 商场共有 5 种进货方案.
∵
例题 &分析
pa
pc
(4)在(2)的条件下,若销售每件甲种纪念品可获利 30元,每件乙种纪念品可获利 12 元,
① 你认为哪种方案获利最大?最大利润是多少?
方法一:逐个计算,比较大小
解: 方案一的利润为:30×30+12×70=1740 元;
方案二的利润为:30×31+12×69=1758元;
方案三的利润为:30×32+12×68=1776元;
方案四的利润为:30×33+12×67=1794元;
方案五的利润为:30×34+12×66=1812元;
方案六的利润为:30×35+12×65=1830元.
∴ 方案六即购甲纪念品35件,购乙纪念品65件时获利最大,
最大利润为1830元.
∵
例题 &分析
方法二 :
即购甲纪念品 35 件,购乙纪念品 65 件时获利最大,
且最大利润为 18×35+1200 = 1830 元.
设商场销售利润为 w 元,根据题意可知:
∵ 18 > 0
函数思想
方法三:
∴ 购买甲纪念品越多,利润越大,
即购甲纪念品 35 件,购乙纪念品 65 件时获利最大.
最大利润为 30×35+12×65 = 1830元.
∵ 30 >12
例题 &分析
pa
pc
若商家保持两种纪念品的售价不变,请你根据以上信息,设计出使这100件纪念品销售总利润最大的进货方案.
(4)在(2)的条件下,若销售每件甲种纪念品可获利 30元,每件乙种纪念品可获利 12 元,
设商场销售总利润为 w 元 .
分类讨论
解:由题意可知 ,销售每件甲种纪念品可获利(30 - m)元 .
同课章节目录
