人教版数学九年级上册 24.2《点和圆、直线和圆的位置关系》(第3课时)课件(共15张PPT)
文档属性
| 名称 | 人教版数学九年级上册 24.2《点和圆、直线和圆的位置关系》(第3课时)课件(共15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 423.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 18:31:06 | ||
图片预览





文档简介
(共15张PPT)
24.2 点和圆、直线和圆的 位置关系(第3课时)
九年级 上册
直线和圆相切是直线和圆的位置关系中特殊并且重要的一种,圆的切线是连接直线型与曲线型的重要桥梁,是研究三角形内切圆、切线长定理和正多边形与圆的关系的基础.
切线的判定定理与性质定理揭示了直线和圆的半径的特殊位置关系,即,切线过半径外端并与这条半径垂直.两个定理互为逆命题.切线判定定理的探究过程体现了由一般到特殊的研究方法.
课件说明
学习目标: 1.理解切线的判定定理与性质定理; 2.会应用切线的判定定理和性质定理解决简单问题.
学习重点: 切线的判定定理和性质定理的应用.
课件说明
1.直线和圆有哪些位置关系?
2.如何判断直线和圆相切?
1.复习直线和圆的位置关系
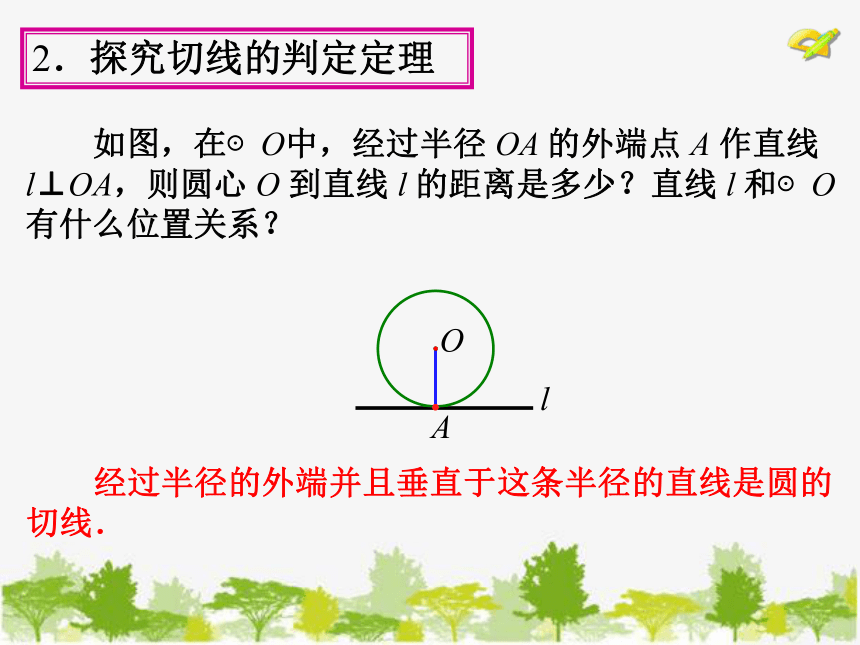
如图,在⊙O中,经过半径 OA 的外端点 A 作直线 l⊥OA,则圆心 O 到直线 l 的距离是多少?直线 l 和⊙O 有什么位置关系?
2.探究切线的判定定理
经过半径的外端并且垂直于这条半径的直线是圆的 切线.
l
O
A
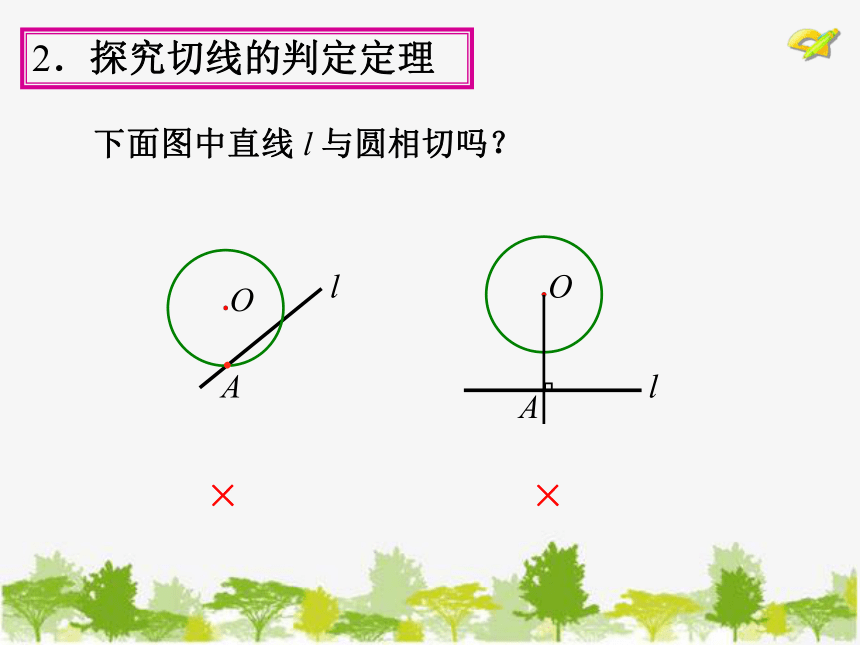
下面图中直线 l 与圆相切吗?
2.探究切线的判定定理
l
O
A
l
O
A
×
×
下雨天当你快速转动雨伞时飞出的水珠,在砂轮上 打磨工件时飞出的火星中,存在与圆相切的现象吗?
2.探究切线的判定定理
已知一个圆和圆上的一点,如何过这个点画出圆的切线?
2.探究切线的判定定理
O
A
将本课件第 5 页中的问题反过来,如图,在⊙O 中,如果直线 l 是⊙O 的切线,切点为 A,那么半径 OA 与直线 l 是不是一定垂直呢?
3.探究切线的性质定理
圆的切线垂直于过切点的半径.
l
O
A
例 已知:△ABC 为等腰三角形,O 是底边 BC 的中点,腰 AB 与⊙O 相切于点 D. 求证: AC 是⊙O 的切线.
4.运用切线的性质和判定定理解决简单问题
A
B
O
D
C
(1)切线的判定方法有几种?结合已知,你选择
哪种判定方法?(切线的判定定理.) (2)要证明切线需要什么条件?如何添加辅助线? (只要证明由点O向 AC 所作的垂线段OE是⊙O的半径
就可以了.所以过圆心 O 作 OE⊥AC ,垂足为E ,连接 OD ,OA .)
在运用切线的判定定理和性质定理时,应如何添加 辅助线?
4.运用切线的性质和判定定理解决简单问题
教科书第 98 页 练习第 1,2 题.
4.运用切线的性质和判定定理解决简单问题
(1)切线的判定定理与性质定理是什么?它们有 怎样的联系?
(2)在应用切线的判定定理和性质定理时,需要 注意什么?
5.课堂小结
教科书习题 24.2 第 4,5,12 题.
6.布置作业
24.2 点和圆、直线和圆的 位置关系(第3课时)
九年级 上册
直线和圆相切是直线和圆的位置关系中特殊并且重要的一种,圆的切线是连接直线型与曲线型的重要桥梁,是研究三角形内切圆、切线长定理和正多边形与圆的关系的基础.
切线的判定定理与性质定理揭示了直线和圆的半径的特殊位置关系,即,切线过半径外端并与这条半径垂直.两个定理互为逆命题.切线判定定理的探究过程体现了由一般到特殊的研究方法.
课件说明
学习目标: 1.理解切线的判定定理与性质定理; 2.会应用切线的判定定理和性质定理解决简单问题.
学习重点: 切线的判定定理和性质定理的应用.
课件说明
1.直线和圆有哪些位置关系?
2.如何判断直线和圆相切?
1.复习直线和圆的位置关系
如图,在⊙O中,经过半径 OA 的外端点 A 作直线 l⊥OA,则圆心 O 到直线 l 的距离是多少?直线 l 和⊙O 有什么位置关系?
2.探究切线的判定定理
经过半径的外端并且垂直于这条半径的直线是圆的 切线.
l
O
A
下面图中直线 l 与圆相切吗?
2.探究切线的判定定理
l
O
A
l
O
A
×
×
下雨天当你快速转动雨伞时飞出的水珠,在砂轮上 打磨工件时飞出的火星中,存在与圆相切的现象吗?
2.探究切线的判定定理
已知一个圆和圆上的一点,如何过这个点画出圆的切线?
2.探究切线的判定定理
O
A
将本课件第 5 页中的问题反过来,如图,在⊙O 中,如果直线 l 是⊙O 的切线,切点为 A,那么半径 OA 与直线 l 是不是一定垂直呢?
3.探究切线的性质定理
圆的切线垂直于过切点的半径.
l
O
A
例 已知:△ABC 为等腰三角形,O 是底边 BC 的中点,腰 AB 与⊙O 相切于点 D. 求证: AC 是⊙O 的切线.
4.运用切线的性质和判定定理解决简单问题
A
B
O
D
C
(1)切线的判定方法有几种?结合已知,你选择
哪种判定方法?(切线的判定定理.) (2)要证明切线需要什么条件?如何添加辅助线? (只要证明由点O向 AC 所作的垂线段OE是⊙O的半径
就可以了.所以过圆心 O 作 OE⊥AC ,垂足为E ,连接 OD ,OA .)
在运用切线的判定定理和性质定理时,应如何添加 辅助线?
4.运用切线的性质和判定定理解决简单问题
教科书第 98 页 练习第 1,2 题.
4.运用切线的性质和判定定理解决简单问题
(1)切线的判定定理与性质定理是什么?它们有 怎样的联系?
(2)在应用切线的判定定理和性质定理时,需要 注意什么?
5.课堂小结
教科书习题 24.2 第 4,5,12 题.
6.布置作业
同课章节目录
