人教版数学九年级下册第二十九章投影与视图 章末复习(教案)
文档属性
| 名称 | 人教版数学九年级下册第二十九章投影与视图 章末复习(教案) |  | |
| 格式 | doc | ||
| 文件大小 | 232.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 10:58:04 | ||
图片预览

文档简介
章末复习
【知识与技能】
1.进一步理解投影、三视图等概念.
2.能画出几何体的三视图,能根据三视图想象物体的形状.
【过程与方法】
通过对具体实例的评析加深对本章知识的理解,感受到三视图、平面展开图与各立体图形之间的相互转化关系.
【情感态度】
关注有关生活中的投影,生产中的三视图问题,提高数学应用意识,增强学生的空间想象能力.
【教学重点】
进一步加深对本章知识的理解,提高解题技能
【教学难点】
利用三视图想象实物形状,并根据相关数据进行计算.
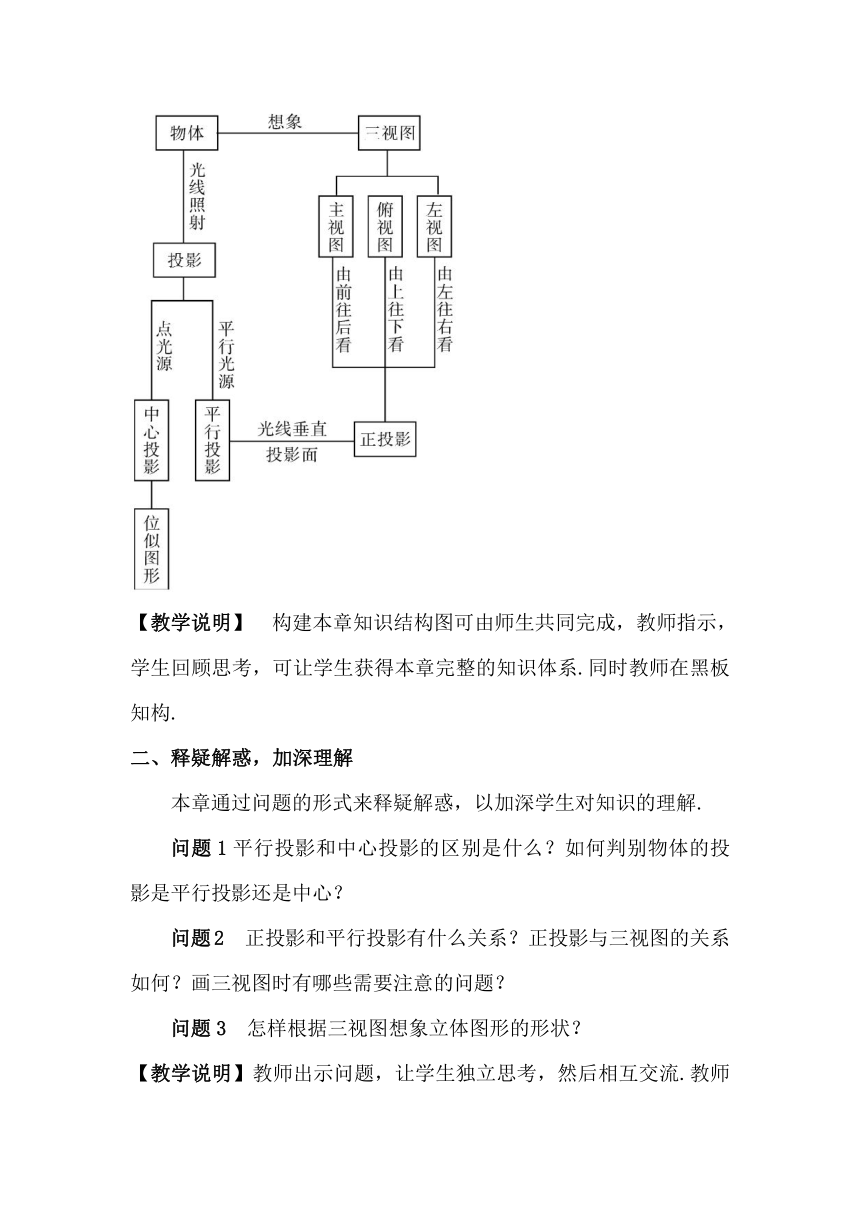
1、 知识框图,整体把握
【教学说明】 构建本章知识结构图可由师生共同完成,教师指示,学生回顾思考,可让学生获得本章完整的知识体系.同时教师在黑板 知构.
二、释疑解惑,加深理解
本章通过问题的形式来释疑解惑,以加深学生对知识的理解.
问题1平行投影和中心投影的区别是什么?如何判别物体的投影是平行投影还是中心?
问题2 正投影和平行投影有什么关系?正投影与三视图的关系如何?画三视图时有哪些需要注意的问题?
问题3 怎样根据三视图想象立体图形的形状?
【教学说明】教师出示问题,让学生独立思考,然后相互交流.教师在巡视中听取学生的观点,看学生有哪些地方存在误区,对此教师要 予以纠正,然后作出系统的说明.
三、典例精析,复习新知
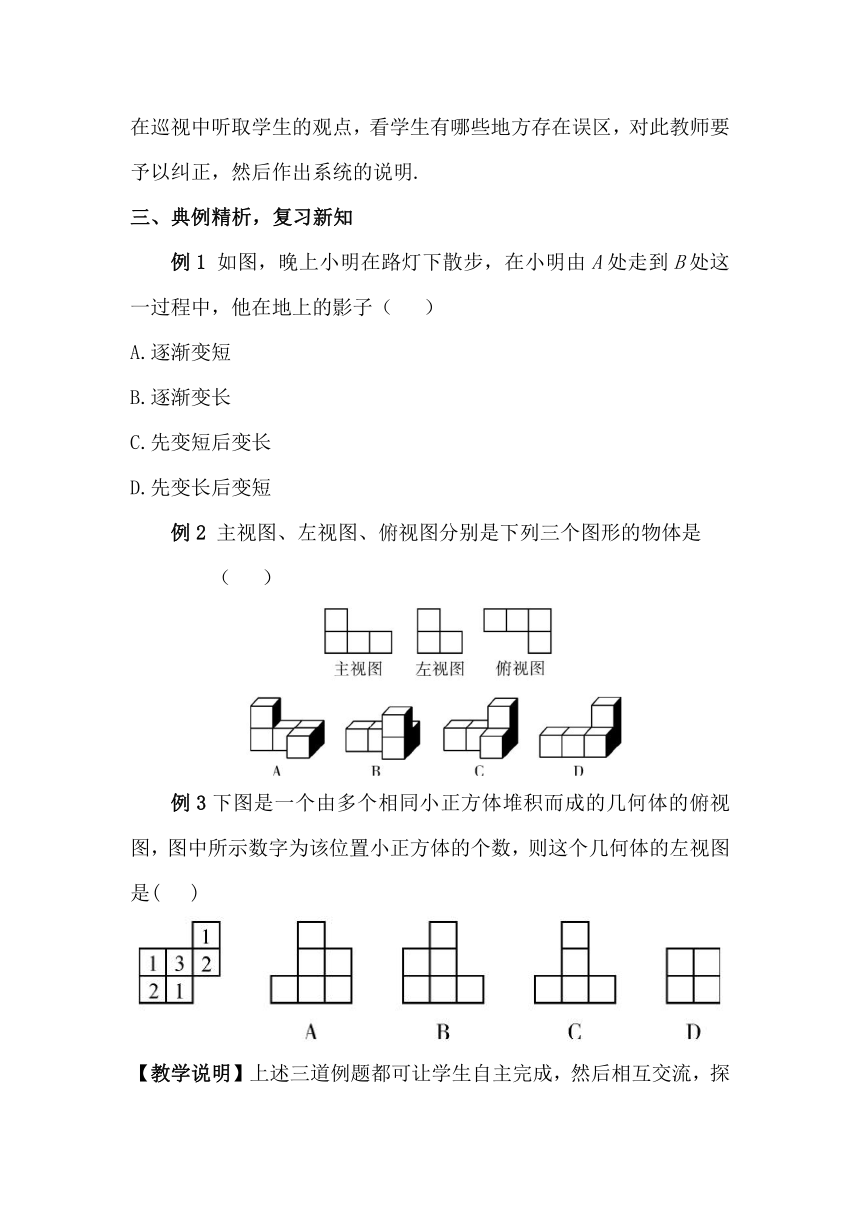
例1 如图,晚上小明在路灯下散步,在小明由A处走到B处这一过程中,他在地上的影子( )
A.逐渐变短
B.逐渐变长
C.先变短后变长
D.先变长后变短
例2 主视图、左视图、俯视图分别是下列三个图形的物体是
( )
例3下图是一个由多个相同小正方体堆积而成的几何体的俯视图,图中所示数字为该位置小正方体的个数,则这个几何体的左视图 是( )
【教学说明】上述三道例题都可让学生自主完成,然后相互交流,探讨出正确结论.出现失误的学生在自查中反思,加深对知识的理解. 其中例3中小正方形内数字所表示的意义是解题关键.
例4 由一些大小相同的小立方体组成的简单几何体的主视图和俯视图如图所示.
(1)请你画出这个几何体的一种左视图;
(2)若组成这个几何体的小正方体的块数为n,求n的值.
【分析】从俯视图可看出这个几何体有前后两排,前排并排有三个正方形,后排有两个正方形,从主视图可看出这个几何体分为左、中、右三列,左列最多只有一个立方块,中列最多有两个立方块,右列最多有三个立方块.由于这个几何体的左视图没有画出,故无法确定这个几何体的形状,但可知道这个几何体最少需要8个立方块,最多有11个立方块,而n=8,9,10,11四个值.它的左视图有或
或或四种可能.
【教学说明】本例的目的是让学生明确确定一个几何体必须从三个角度得到它的视图才行,仅有其中一个或两个都是不可能的.同时,通过本例可进一步加深学生的空间观念和分类讨论问题的能力.教学时仍可让学生先尝试着解决,最后教师予以评讲.
例5 如图是某种物体的三视图及相关数据(单位:cm),求该物体的体积(,π=3.14,精确 到 0.01cm3).
【分析】由三视图可想象出这个物体应该是一个正六棱柱中央挖出了一个圆柱,其体积为V≈1.16cm3.
例6 如图所示,点P表示广场上的一盏照明灯.
(1)请你在图中画出小敏在照明灯P照射下的影子(用线段表示);
(2)若小丽到灯柱MO的距离为4.5米,照明灯P到灯柱的距离为1.5米,小丽目测照明灯P的仰角为55°,她的目高QB为1.6米,试求照明灯到地面的距离(结果精确到0.1米).(参考数据:tan55°≈1.428,sin55°≈0.819,cos55°≈0.574)
【分析】在(1)中,只需连接小敏的头的顶部(记为D)与点P连线,交地面(AB所在直线)于点C,则线段AC的长即为小敏在灯P下的影子(即图中粗线AC);在(2)中,过P作PH垂直于过Q点的水平线于H,即PH丄QH,再求PH的长即可.
【教学说明】本例是一道投影和解直角三角形的综合问题,难度不大,学生能独立完成.教师在给出问题后,巡视全场,帮助学生完成解答.
四、师生互动,课堂小结
1.通过这节课的学习你有哪些问题?
2.回顾本章知识,你还有哪些问题?
【教学说明】学生相互交流,进一步加深对本章知识的理解,针对学生存在的疑问,可当堂解决,也可课后个别辅导,帮助他(她)完善对本章知识的认知.
1.布置作业:从教材P109 111复习题29中选取.
2.完成创优作业中本课时的练习.
本课时通过知识框图和例题的讲解,力求让学生对本章知识了然于胸,教师在教学时应注意让学生在全面掌握知识点的基础上抓住重点、举一反三.
【知识与技能】
1.进一步理解投影、三视图等概念.
2.能画出几何体的三视图,能根据三视图想象物体的形状.
【过程与方法】
通过对具体实例的评析加深对本章知识的理解,感受到三视图、平面展开图与各立体图形之间的相互转化关系.
【情感态度】
关注有关生活中的投影,生产中的三视图问题,提高数学应用意识,增强学生的空间想象能力.
【教学重点】
进一步加深对本章知识的理解,提高解题技能
【教学难点】
利用三视图想象实物形状,并根据相关数据进行计算.
1、 知识框图,整体把握
【教学说明】 构建本章知识结构图可由师生共同完成,教师指示,学生回顾思考,可让学生获得本章完整的知识体系.同时教师在黑板 知构.
二、释疑解惑,加深理解
本章通过问题的形式来释疑解惑,以加深学生对知识的理解.
问题1平行投影和中心投影的区别是什么?如何判别物体的投影是平行投影还是中心?
问题2 正投影和平行投影有什么关系?正投影与三视图的关系如何?画三视图时有哪些需要注意的问题?
问题3 怎样根据三视图想象立体图形的形状?
【教学说明】教师出示问题,让学生独立思考,然后相互交流.教师在巡视中听取学生的观点,看学生有哪些地方存在误区,对此教师要 予以纠正,然后作出系统的说明.
三、典例精析,复习新知
例1 如图,晚上小明在路灯下散步,在小明由A处走到B处这一过程中,他在地上的影子( )
A.逐渐变短
B.逐渐变长
C.先变短后变长
D.先变长后变短
例2 主视图、左视图、俯视图分别是下列三个图形的物体是
( )
例3下图是一个由多个相同小正方体堆积而成的几何体的俯视图,图中所示数字为该位置小正方体的个数,则这个几何体的左视图 是( )
【教学说明】上述三道例题都可让学生自主完成,然后相互交流,探讨出正确结论.出现失误的学生在自查中反思,加深对知识的理解. 其中例3中小正方形内数字所表示的意义是解题关键.
例4 由一些大小相同的小立方体组成的简单几何体的主视图和俯视图如图所示.
(1)请你画出这个几何体的一种左视图;
(2)若组成这个几何体的小正方体的块数为n,求n的值.
【分析】从俯视图可看出这个几何体有前后两排,前排并排有三个正方形,后排有两个正方形,从主视图可看出这个几何体分为左、中、右三列,左列最多只有一个立方块,中列最多有两个立方块,右列最多有三个立方块.由于这个几何体的左视图没有画出,故无法确定这个几何体的形状,但可知道这个几何体最少需要8个立方块,最多有11个立方块,而n=8,9,10,11四个值.它的左视图有或
或或四种可能.
【教学说明】本例的目的是让学生明确确定一个几何体必须从三个角度得到它的视图才行,仅有其中一个或两个都是不可能的.同时,通过本例可进一步加深学生的空间观念和分类讨论问题的能力.教学时仍可让学生先尝试着解决,最后教师予以评讲.
例5 如图是某种物体的三视图及相关数据(单位:cm),求该物体的体积(,π=3.14,精确 到 0.01cm3).
【分析】由三视图可想象出这个物体应该是一个正六棱柱中央挖出了一个圆柱,其体积为V≈1.16cm3.
例6 如图所示,点P表示广场上的一盏照明灯.
(1)请你在图中画出小敏在照明灯P照射下的影子(用线段表示);
(2)若小丽到灯柱MO的距离为4.5米,照明灯P到灯柱的距离为1.5米,小丽目测照明灯P的仰角为55°,她的目高QB为1.6米,试求照明灯到地面的距离(结果精确到0.1米).(参考数据:tan55°≈1.428,sin55°≈0.819,cos55°≈0.574)
【分析】在(1)中,只需连接小敏的头的顶部(记为D)与点P连线,交地面(AB所在直线)于点C,则线段AC的长即为小敏在灯P下的影子(即图中粗线AC);在(2)中,过P作PH垂直于过Q点的水平线于H,即PH丄QH,再求PH的长即可.
【教学说明】本例是一道投影和解直角三角形的综合问题,难度不大,学生能独立完成.教师在给出问题后,巡视全场,帮助学生完成解答.
四、师生互动,课堂小结
1.通过这节课的学习你有哪些问题?
2.回顾本章知识,你还有哪些问题?
【教学说明】学生相互交流,进一步加深对本章知识的理解,针对学生存在的疑问,可当堂解决,也可课后个别辅导,帮助他(她)完善对本章知识的认知.
1.布置作业:从教材P109 111复习题29中选取.
2.完成创优作业中本课时的练习.
本课时通过知识框图和例题的讲解,力求让学生对本章知识了然于胸,教师在教学时应注意让学生在全面掌握知识点的基础上抓住重点、举一反三.
