安徽省滁州市定远县育才学校2022年普通高中高二学业水平测试卷数学试题(一)(6月)(Word版含解析)
文档属性
| 名称 | 安徽省滁州市定远县育才学校2022年普通高中高二学业水平测试卷数学试题(一)(6月)(Word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 458.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 11:26:15 | ||
图片预览



文档简介
定远育才学校2022年普通高中学业水平测试卷
数学(一)
(必修1集合与常用逻辑用语,函数的基本概念和性质)
本试卷分第I卷和第Ⅱ卷两部分。第I卷为选择题,第Ⅱ卷为非选择题。全卷
共25题,满分100分,考试时间90分钟。
第I卷(选择题共54分)
一、选择题(本大题共18小题,每小题3分,满分54分,每小题4个选项中,只有一个选项符合题目要求)
1.设集合,,则集合和集合的关系是
A. B. C. D. ( )
2.已知集合,则集合A的子集个数为( )
A.8 B.16 C.32 D.64
3.已知全集,集合,,则等于( )
A. B. C. D.
4.设集合,,则( )
A. B.
C. D.
5.已知全集U=R,则正确表示集合M= {-1,0,1} 和N={ x |x+x=0} 关系的韦恩(Venn)图是( )
A. B. C. D.
6.函数+的定义域为( )
A. B.(-∞,3)∪(3,+∞)
C.(3,+∞) D.(3,+∞)
7.函数则( )
A. B. C. D.
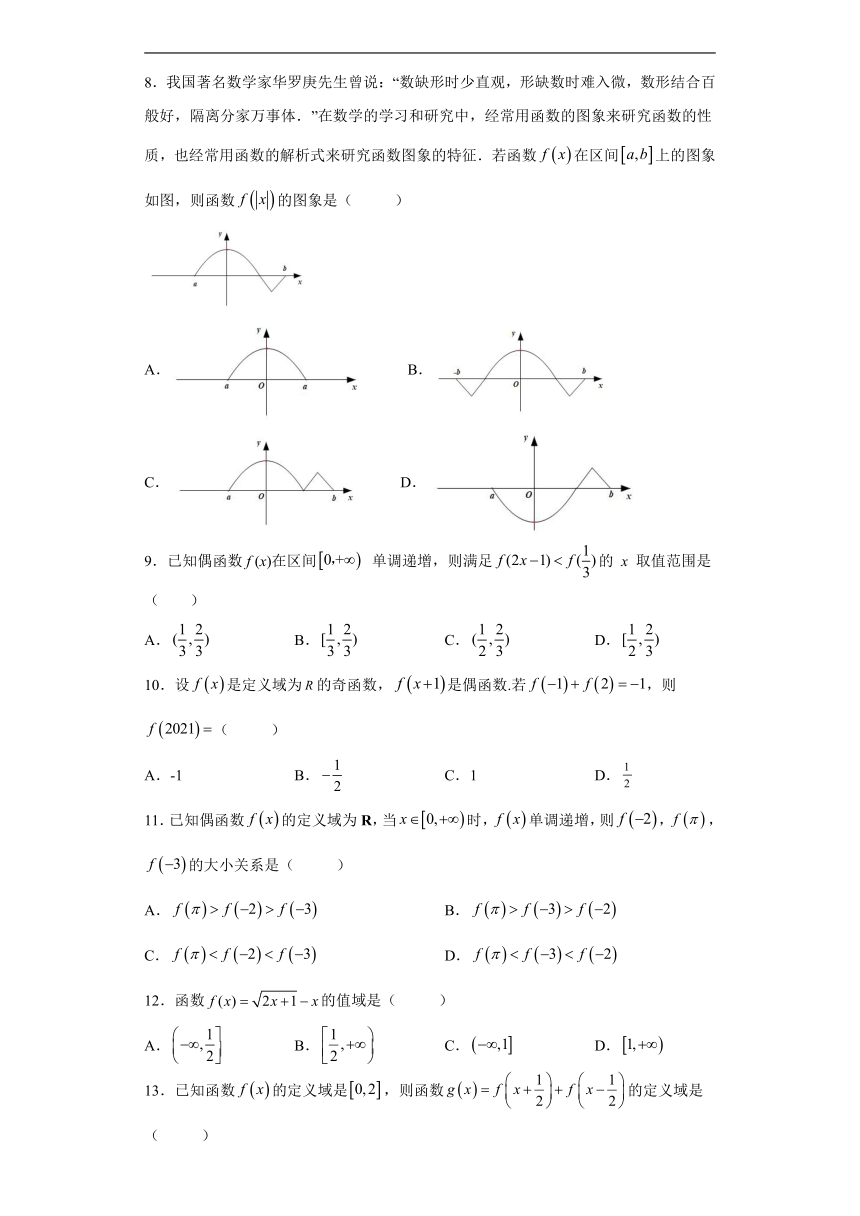
8.我国著名数学家华罗庚先生曾说:“数缺形时少直观,形缺数时难入微,数形结合百般好,隔离分家万事体.”在数学的学习和研究中,经常用函数的图象来研究函数的性质,也经常用函数的解析式来研究函数图象的特征.若函数在区间上的图象如图,则函数的图象是( )
A. B.
C. D.
9.已知偶函数f (x)在区间 单调递增,则满足的 x 取值范围是( )
A. B. C. D.
10.设是定义域为的奇函数,是偶函数.若,则( )
A.-1 B. C.1 D.
11.已知偶函数的定义域为R,当时,单调递增,则,,的大小关系是( )
A. B.
C. D.
12.函数的值域是( )
A. B. C. D.
13.已知函数的定义域是,则函数的定义域是( )
A. B. C. D.
14.已知函数,且,则( )
A.1或 B.1或 C.或2 D.1或或
15.已知函数的定义域为,满足:①对任意,都有,②对任意且,都有,则函数叫“成功函数”,下列函数是“成功函数”的是( )
A. B.
C. D.
16.“”是“函数是定义在上的奇函数”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
17.已知命题,,则是( )
A., B.,
C., D.,
18.下列命题中是全称量词命题,并且又是真命题的是( )
A.是无理数 B.,使为偶数
C.对任意,都有 D.所有菱形的四条边都相等
第II卷(非选择题 共46分)
二、填空题(本大题共4小题,每小题4分,满分16分,把答案写在题中的横线上)
19.已知集合,则的非空真子集的个数为__________.
20.已知则________.
21.已知函数在定义域(-1,1)上是减函数,且,则的取值范围是______.
22.若定义在R上的奇函数单调递减,则不等式的解集为________.
三、解答题(本大题共3小题,每小题10分,满分30分,解答应写出文字说明及演算步骤)
23.已知集合A={x|2≤x≤8},B={x|1a},U=R.
(1)求A∪B,;
(2)若A∩C≠ ,求a的取值范围.
24.已知,p:,q:,
(1)若p是q的充分条件,求实数m的取值范围;
(2)若,命题p,q中有且仅有一个是真命题,求实数x的取值范围.
25.(1)已知函数,求的解析式;
(2)已知为二次函数,且,,求的解析式.
参考答案
1.C由 , ,可知, , 故选 C .
2.B∵,∴,解得,∵,∴,则集合的子集个数为.故选:B.
3.C因为,,所以,又,所以;
故选:C
4.A由题意,集合,,
根据集合并集的概念及运算,可得.故选:A.
5.B由N={x|x2+x=0},得N={﹣1,0}.∵M={﹣1,0,1},∴N M,故选B.
6.C要使函数+有意义,则
所以,解得且,
所以函数+的定义域为∪(3,+∞).故选:C.
7.D.故选:D.
8.B图象的构成如下:时,图象与图象相同;时,图象与时的图象关于轴对称,
由此可知函数的图象是B.故选:B
9.A因为偶函数在区间上单调递增,
所以在区间上单调递减,故越靠近轴,函数值越小,
因为,
所以,解得:.故选:A.
10.C由为R上的奇函数,得,且,
由为偶函数,得图象关于直线对称,则,
所以,即,
则,即,
所以函数是周期为4的周期函数,
又,由,得
所以.故选:C
11.B因为为偶函数,所以,.又当时,单调递增,且,所以,即.故选:B.
12.C由题意,函数的定义域为
令
故
由于为开口向下的二次函数,对称轴为
故当时,,无最小值
故函数的值域是故选:C
13.A因为函数的定义域是,所以有:.故选:A
14.A当时,,
解得(舍去);
当时,,
解得(舍去).
综上,或.故选:A
15.B由任意,都有知是奇函数,
由任意且,
都有,知是增函数,
因为在定义域上是奇函数,
但在定义域上不是单增函数,故A错;
因为是奇函数,,
所以在定义域上是增函数,故B正确;
因为在定义域是减函数,故C错;
因为在上单调递减,故D错.故选:B.
16.B若,函数不一定是定义在上的奇函数,
若函数是定义在上的奇函数,则,
因此“”是“函数是定义在上的奇函数”的必要不充分条件,故选:B.
17.D命题为全称命题,该命题的否定为,,故选:D.
18.D对于A,是特称命题;
对于B,是特称命题,是假命题;
对于C,是全称命题,而,所以是假命题;
对于D,是全称命题,是真命题,故选:D
19.2的非空真子集的个数为.故答案为:2
20.,故答案为:.
21.由题意,函数在定义域(-1,1)上是减函数,且
故解得:故答案为:
22.是上的奇函数,且单调递减;
由得:;
;
解得;
原不等式的解集为.故答案为:.
23.(1)A∪B={x|1(2){a|a<8}
【解析】 (1)A∪B={x|2≤x≤8}∪{x|1∵={x|x<2或x>8},
∴∩B={x|1(2)∵A∩C,作图易知,只要a在8的左边即可,
∴a<8.
∴a的取值范围为{a|a<8}.
24.(1) (2)
【解析】 (1)不等式的解为,即p:.
因为p是q的充分条件,所以是的子集,
故解得:,所以m的取值范围是.
(2)当时,q:,
由于命题p,q其中一个是真命题,一个是假命题,分以下两种情况讨论:
①p真q假时,与或取交集,解得:;
②p假q真时,与或取交集,解得:或.
所以实数x的取值范围为.
25.(1);(2).
【解析】(1)设,可得,则,
故;
(2)因为,可设,
则,解得,因此,.
数学(一)
(必修1集合与常用逻辑用语,函数的基本概念和性质)
本试卷分第I卷和第Ⅱ卷两部分。第I卷为选择题,第Ⅱ卷为非选择题。全卷
共25题,满分100分,考试时间90分钟。
第I卷(选择题共54分)
一、选择题(本大题共18小题,每小题3分,满分54分,每小题4个选项中,只有一个选项符合题目要求)
1.设集合,,则集合和集合的关系是
A. B. C. D. ( )
2.已知集合,则集合A的子集个数为( )
A.8 B.16 C.32 D.64
3.已知全集,集合,,则等于( )
A. B. C. D.
4.设集合,,则( )
A. B.
C. D.
5.已知全集U=R,则正确表示集合M= {-1,0,1} 和N={ x |x+x=0} 关系的韦恩(Venn)图是( )
A. B. C. D.
6.函数+的定义域为( )
A. B.(-∞,3)∪(3,+∞)
C.(3,+∞) D.(3,+∞)
7.函数则( )
A. B. C. D.
8.我国著名数学家华罗庚先生曾说:“数缺形时少直观,形缺数时难入微,数形结合百般好,隔离分家万事体.”在数学的学习和研究中,经常用函数的图象来研究函数的性质,也经常用函数的解析式来研究函数图象的特征.若函数在区间上的图象如图,则函数的图象是( )
A. B.
C. D.
9.已知偶函数f (x)在区间 单调递增,则满足的 x 取值范围是( )
A. B. C. D.
10.设是定义域为的奇函数,是偶函数.若,则( )
A.-1 B. C.1 D.
11.已知偶函数的定义域为R,当时,单调递增,则,,的大小关系是( )
A. B.
C. D.
12.函数的值域是( )
A. B. C. D.
13.已知函数的定义域是,则函数的定义域是( )
A. B. C. D.
14.已知函数,且,则( )
A.1或 B.1或 C.或2 D.1或或
15.已知函数的定义域为,满足:①对任意,都有,②对任意且,都有,则函数叫“成功函数”,下列函数是“成功函数”的是( )
A. B.
C. D.
16.“”是“函数是定义在上的奇函数”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
17.已知命题,,则是( )
A., B.,
C., D.,
18.下列命题中是全称量词命题,并且又是真命题的是( )
A.是无理数 B.,使为偶数
C.对任意,都有 D.所有菱形的四条边都相等
第II卷(非选择题 共46分)
二、填空题(本大题共4小题,每小题4分,满分16分,把答案写在题中的横线上)
19.已知集合,则的非空真子集的个数为__________.
20.已知则________.
21.已知函数在定义域(-1,1)上是减函数,且,则的取值范围是______.
22.若定义在R上的奇函数单调递减,则不等式的解集为________.
三、解答题(本大题共3小题,每小题10分,满分30分,解答应写出文字说明及演算步骤)
23.已知集合A={x|2≤x≤8},B={x|1
(1)求A∪B,;
(2)若A∩C≠ ,求a的取值范围.
24.已知,p:,q:,
(1)若p是q的充分条件,求实数m的取值范围;
(2)若,命题p,q中有且仅有一个是真命题,求实数x的取值范围.
25.(1)已知函数,求的解析式;
(2)已知为二次函数,且,,求的解析式.
参考答案
1.C由 , ,可知, , 故选 C .
2.B∵,∴,解得,∵,∴,则集合的子集个数为.故选:B.
3.C因为,,所以,又,所以;
故选:C
4.A由题意,集合,,
根据集合并集的概念及运算,可得.故选:A.
5.B由N={x|x2+x=0},得N={﹣1,0}.∵M={﹣1,0,1},∴N M,故选B.
6.C要使函数+有意义,则
所以,解得且,
所以函数+的定义域为∪(3,+∞).故选:C.
7.D.故选:D.
8.B图象的构成如下:时,图象与图象相同;时,图象与时的图象关于轴对称,
由此可知函数的图象是B.故选:B
9.A因为偶函数在区间上单调递增,
所以在区间上单调递减,故越靠近轴,函数值越小,
因为,
所以,解得:.故选:A.
10.C由为R上的奇函数,得,且,
由为偶函数,得图象关于直线对称,则,
所以,即,
则,即,
所以函数是周期为4的周期函数,
又,由,得
所以.故选:C
11.B因为为偶函数,所以,.又当时,单调递增,且,所以,即.故选:B.
12.C由题意,函数的定义域为
令
故
由于为开口向下的二次函数,对称轴为
故当时,,无最小值
故函数的值域是故选:C
13.A因为函数的定义域是,所以有:.故选:A
14.A当时,,
解得(舍去);
当时,,
解得(舍去).
综上,或.故选:A
15.B由任意,都有知是奇函数,
由任意且,
都有,知是增函数,
因为在定义域上是奇函数,
但在定义域上不是单增函数,故A错;
因为是奇函数,,
所以在定义域上是增函数,故B正确;
因为在定义域是减函数,故C错;
因为在上单调递减,故D错.故选:B.
16.B若,函数不一定是定义在上的奇函数,
若函数是定义在上的奇函数,则,
因此“”是“函数是定义在上的奇函数”的必要不充分条件,故选:B.
17.D命题为全称命题,该命题的否定为,,故选:D.
18.D对于A,是特称命题;
对于B,是特称命题,是假命题;
对于C,是全称命题,而,所以是假命题;
对于D,是全称命题,是真命题,故选:D
19.2的非空真子集的个数为.故答案为:2
20.,故答案为:.
21.由题意,函数在定义域(-1,1)上是减函数,且
故解得:故答案为:
22.是上的奇函数,且单调递减;
由得:;
;
解得;
原不等式的解集为.故答案为:.
23.(1)A∪B={x|1
【解析】 (1)A∪B={x|2≤x≤8}∪{x|1
∴∩B={x|1
∴a<8.
∴a的取值范围为{a|a<8}.
24.(1) (2)
【解析】 (1)不等式的解为,即p:.
因为p是q的充分条件,所以是的子集,
故解得:,所以m的取值范围是.
(2)当时,q:,
由于命题p,q其中一个是真命题,一个是假命题,分以下两种情况讨论:
①p真q假时,与或取交集,解得:;
②p假q真时,与或取交集,解得:或.
所以实数x的取值范围为.
25.(1);(2).
【解析】(1)设,可得,则,
故;
(2)因为,可设,
则,解得,因此,.
同课章节目录
