沪科版数学八年级上册第15章轴对称图形与等腰三角形练习(word解析版)
文档属性
| 名称 | 沪科版数学八年级上册第15章轴对称图形与等腰三角形练习(word解析版) |
|
|
| 格式 | docx | ||
| 文件大小 | 234.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-17 00:00:00 | ||
图片预览



文档简介
小结评价
类型之一 轴对称与轴对称图形
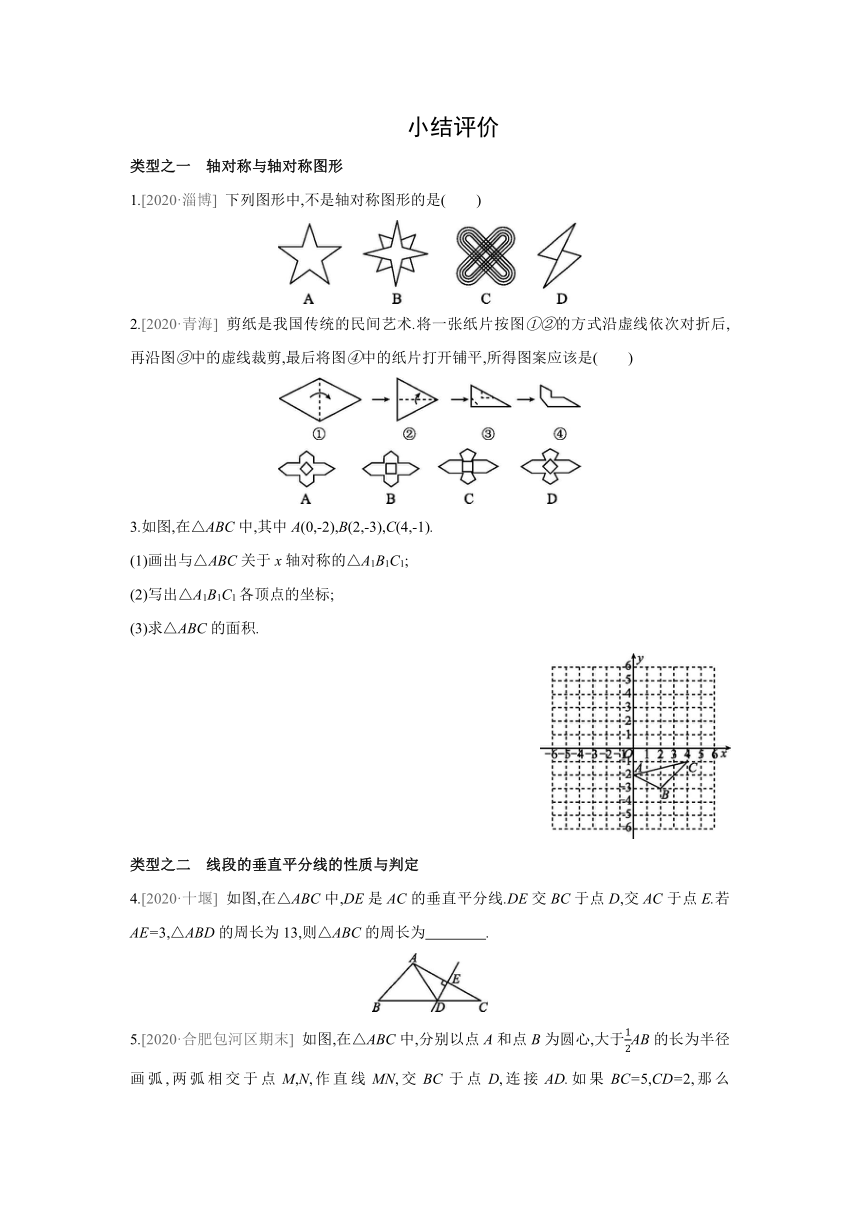
1.[2020·淄博] 下列图形中,不是轴对称图形的是( )
2.[2020·青海] 剪纸是我国传统的民间艺术.将一张纸片按图①②的方式沿虚线依次对折后,再沿图③中的虚线裁剪,最后将图④中的纸片打开铺平,所得图案应该是( )
3.如图,在△ABC中,其中A(0,-2),B(2,-3),C(4,-1).
(1)画出与△ABC关于x轴对称的△A1B1C1;
(2)写出△A1B1C1各顶点的坐标;
(3)求△ABC的面积.
类型之二 线段的垂直平分线的性质与判定
4.[2020·十堰] 如图,在△ABC中,DE是AC的垂直平分线.DE交BC于点D,交AC于点E.若AE=3,△ABD的周长为13,则△ABC的周长为 .
5.[2020·合肥包河区期末] 如图,在△ABC中,分别以点A和点B为圆心,大于AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.如果BC=5,CD=2,那么AD= .
6.在△ABC中,DE垂直平分AB,分别交AB,BC于点D,E,MN垂直平分AC,分别交AC,BC于点M,N.
(1)如图①,若∠BAC=110°,则∠EAN的度数是 ;
(2)如图②,若∠BAC=80°,则∠EAN的度数是 ;
(3)若∠BAC=α(α≠90°),则∠EAN的度数为 (用含α的代数式表示).
类型之三 等腰三角形的性质与判定
7.如图,在等边三角形ABC中,AD是∠BAC的平分线,E为AD上一点,以BE为一边且在BE下方作等边三角形BEF,连接CF.
(1)求证:AE=CF;
(2)求∠ACF的度数.
8.[2020·绍兴] 问题:如图,在△ABD中,BA=BD.在BD的延长线上取点E,C,作△AEC,使EA=EC.若∠BAE=90°,∠B=45°,求∠DAC的度数.
答案:∠DAC=45°.
思考:(1)如果把以上“问题”中的条件“∠B=45°”去掉,其余条件不变,那么∠DAC的度数会改变吗 请说明理由;
(2)如果把以上“问题”中的条件“∠B=45°”去掉,再将“∠BAE=90°”改为“∠BAE=n°”,其余条件不变,求∠DAC的度数.
类型之四 角的平分线的性质与判定
9.[2020·合肥庐阳区期末] 如图,已知在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD的面积是( )
A.24 B.30 C.36 D.42
10.[2020·芜湖期末] 如图,在锐角三角形ABC中,AB=4,△ABC的面积为8,BD平分∠ABC.若M,N分别是BD,BC上的动点,则CM+MN的最小值是( )
A.2 B.4 C.6 D.8
类型之五 数学活动
11.在△ABC中,∠ACB=2∠B,如图①,当∠C=90°,AD为∠BAC的平分线时,在AB上截取AE=AC,连接DE,易证AB=AC+CD.
(1)如图②,当∠C≠90°,AD为△ABC的角平分线时,线段AB,AC,CD又有怎样的数量关系 不需要证明,请直接写出你的猜想;
(2)如图③,当AD为△ABC的外角平分线且交BC的延长线于点D时,线段AB,AC,CD又有怎样的数量关系 请写出你的猜想,并对你的猜想给予证明.
教师详解详析
1.D [解析] 根据轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,只有选项D不是轴对称图形.
2.A
3.解:(1)如图所示,△A1B1C1即为所求.
(2)A1(0,2),B1(2,3),C1(4,1).
(3)S△ABC=2×4-×2×2-×4×1-×2×1=3.
4.19 [解析] ∵DE是AC的垂直平分线,AE=3,
∴AC=2AE=6,AD=DC,
∵AB+BD+AD=13,
∴△ABC的周长=AB+BC+AC=AB+BD+AD+AC=13+6=19.
5.3 [解析] 由作图步骤可得MN垂直平分AB,则AD=BD.
∵BC=5,CD=2,
∴BD=AD=BC-CD=5-2=3.
6.(1)40° (2)20° (3)180°-2α或2α-180°
[解析] (1)∵DE垂直平分AB,
∴AE=BE,
∴∠BAE=∠B.
同理可得∠CAN=∠C.
∴∠EAN=∠BAC-∠BAE-∠CAN=∠BAC-(∠B+∠C).
在△ABC中,∠B+∠C=180°-∠BAC=70°,
∴∠EAN=110°-70°=40°.
(2)∵DE垂直平分AB,
∴AE=BE,
∴∠BAE=∠B.
同理可得∠CAN=∠C.
∴∠EAN=∠BAE+∠CAN-∠BAC=(∠B+∠C)-∠BAC.
在△ABC中,∠B+∠C=180°-∠BAC=100°,
∴∠EAN=100°-80°=20°.
(3)当0°<α<90°时,∠EAN=180°-2α;
当90°<α<180°时,∠EAN=2α-180°.
7.解:(1)证明:∵△ABC是等边三角形,
∴AB=BC,∠ABE+∠EBC=60°.
∵△BEF是等边三角形,
∴EB=FB,∠CBF+∠EBC=60°,
∴∠ABE=∠CBF.
在△ABE和△CBF中,
∵
∴△ABE≌△CBF(SAS),
∴AE=CF.
(2)∵在等边三角形ABC中,AD是∠BAC的平分线,
∴∠BAE=30°,∠ACB=60°.
∵△ABE≌△CBF,
∴∠BCF=∠BAE=30°,
∴∠ACF=∠BCF+∠ACB=30°+60°=90°.
8.解:(1)∠DAC的度数不会改变.理由:
∵EA=EC,
∴∠CAE=∠C.
∵BA=BD,
∴∠BAD=∠BDA.
∵∠BAE=90°,
∴∠B=90°-∠AED=90°-2∠C,
∴∠BAD=(180°-∠B)=[180°-(90°-2∠C)]=45°+∠C,
∴∠DAE=90°-∠BAD=90°-(45°+∠C)=45°-∠C,
∴∠DAC=∠DAE+∠CAE=45°-∠C+∠C=45°.
(2)设∠ABC=m°,则∠BAD=(180°-m°)=90°-m°,∠AEB=180°-n°-m°,
∴∠DAE=n°-∠BAD=n°-90°+m°.
∵EA=EC,
∴∠CAE=∠AEB=90°-n°-m°,
∴∠DAC=∠DAE+∠CAE=n°-90°+m°+90°-n°-m°=n°.
9.B [解析] 过点D作DH⊥AB交BA的延长线于点H.
∵BD平分∠ABC,∠BCD=90°,
∴DH=CD=4,
∴四边形ABCD的面积=S△ABD+S△BCD=AB·DH+BC·CD=×6×4+×9×4=30.
10.B [解析] 过点C作CE⊥AB于点E,交BD于点M',过点M'作M'N'⊥BC于点N'.
∵BD平分∠ABC,M'E⊥AB于点E,M'N'⊥BC于点N',
∴M'N'=M'E,∴CE=CM'+M'E=CM'+M'N',
∴当点M与点M'重合,点N与点N'重合时,CM+MN的值最小.
∵△ABC的面积为8,AB=4,
∴×4·CE=8,
∴CE=4,
即CM+MN的最小值为4.
11.解:(1)猜想:AB=AC+CD.
(2)猜想:AB+AC=CD.
证明:在BA的延长线上截取AE=AC,连接ED.
∵AD平分∠FAC,
∴∠EAD=∠CAD.
在△EAD与△CAD中,
∵
∴△EAD≌△CAD.
∴ED=CD,∠AED=∠ACD.
∴∠FED=∠ACB.
又∵∠ACB=2∠B,∠FED=∠B+∠EDB,
∴∠EDB=∠B.
∴EB=ED.
∴AE+AB=EB=ED=CD.
∴AB+AC=CD.
类型之一 轴对称与轴对称图形
1.[2020·淄博] 下列图形中,不是轴对称图形的是( )
2.[2020·青海] 剪纸是我国传统的民间艺术.将一张纸片按图①②的方式沿虚线依次对折后,再沿图③中的虚线裁剪,最后将图④中的纸片打开铺平,所得图案应该是( )
3.如图,在△ABC中,其中A(0,-2),B(2,-3),C(4,-1).
(1)画出与△ABC关于x轴对称的△A1B1C1;
(2)写出△A1B1C1各顶点的坐标;
(3)求△ABC的面积.
类型之二 线段的垂直平分线的性质与判定
4.[2020·十堰] 如图,在△ABC中,DE是AC的垂直平分线.DE交BC于点D,交AC于点E.若AE=3,△ABD的周长为13,则△ABC的周长为 .
5.[2020·合肥包河区期末] 如图,在△ABC中,分别以点A和点B为圆心,大于AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.如果BC=5,CD=2,那么AD= .
6.在△ABC中,DE垂直平分AB,分别交AB,BC于点D,E,MN垂直平分AC,分别交AC,BC于点M,N.
(1)如图①,若∠BAC=110°,则∠EAN的度数是 ;
(2)如图②,若∠BAC=80°,则∠EAN的度数是 ;
(3)若∠BAC=α(α≠90°),则∠EAN的度数为 (用含α的代数式表示).
类型之三 等腰三角形的性质与判定
7.如图,在等边三角形ABC中,AD是∠BAC的平分线,E为AD上一点,以BE为一边且在BE下方作等边三角形BEF,连接CF.
(1)求证:AE=CF;
(2)求∠ACF的度数.
8.[2020·绍兴] 问题:如图,在△ABD中,BA=BD.在BD的延长线上取点E,C,作△AEC,使EA=EC.若∠BAE=90°,∠B=45°,求∠DAC的度数.
答案:∠DAC=45°.
思考:(1)如果把以上“问题”中的条件“∠B=45°”去掉,其余条件不变,那么∠DAC的度数会改变吗 请说明理由;
(2)如果把以上“问题”中的条件“∠B=45°”去掉,再将“∠BAE=90°”改为“∠BAE=n°”,其余条件不变,求∠DAC的度数.
类型之四 角的平分线的性质与判定
9.[2020·合肥庐阳区期末] 如图,已知在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD的面积是( )
A.24 B.30 C.36 D.42
10.[2020·芜湖期末] 如图,在锐角三角形ABC中,AB=4,△ABC的面积为8,BD平分∠ABC.若M,N分别是BD,BC上的动点,则CM+MN的最小值是( )
A.2 B.4 C.6 D.8
类型之五 数学活动
11.在△ABC中,∠ACB=2∠B,如图①,当∠C=90°,AD为∠BAC的平分线时,在AB上截取AE=AC,连接DE,易证AB=AC+CD.
(1)如图②,当∠C≠90°,AD为△ABC的角平分线时,线段AB,AC,CD又有怎样的数量关系 不需要证明,请直接写出你的猜想;
(2)如图③,当AD为△ABC的外角平分线且交BC的延长线于点D时,线段AB,AC,CD又有怎样的数量关系 请写出你的猜想,并对你的猜想给予证明.
教师详解详析
1.D [解析] 根据轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,只有选项D不是轴对称图形.
2.A
3.解:(1)如图所示,△A1B1C1即为所求.
(2)A1(0,2),B1(2,3),C1(4,1).
(3)S△ABC=2×4-×2×2-×4×1-×2×1=3.
4.19 [解析] ∵DE是AC的垂直平分线,AE=3,
∴AC=2AE=6,AD=DC,
∵AB+BD+AD=13,
∴△ABC的周长=AB+BC+AC=AB+BD+AD+AC=13+6=19.
5.3 [解析] 由作图步骤可得MN垂直平分AB,则AD=BD.
∵BC=5,CD=2,
∴BD=AD=BC-CD=5-2=3.
6.(1)40° (2)20° (3)180°-2α或2α-180°
[解析] (1)∵DE垂直平分AB,
∴AE=BE,
∴∠BAE=∠B.
同理可得∠CAN=∠C.
∴∠EAN=∠BAC-∠BAE-∠CAN=∠BAC-(∠B+∠C).
在△ABC中,∠B+∠C=180°-∠BAC=70°,
∴∠EAN=110°-70°=40°.
(2)∵DE垂直平分AB,
∴AE=BE,
∴∠BAE=∠B.
同理可得∠CAN=∠C.
∴∠EAN=∠BAE+∠CAN-∠BAC=(∠B+∠C)-∠BAC.
在△ABC中,∠B+∠C=180°-∠BAC=100°,
∴∠EAN=100°-80°=20°.
(3)当0°<α<90°时,∠EAN=180°-2α;
当90°<α<180°时,∠EAN=2α-180°.
7.解:(1)证明:∵△ABC是等边三角形,
∴AB=BC,∠ABE+∠EBC=60°.
∵△BEF是等边三角形,
∴EB=FB,∠CBF+∠EBC=60°,
∴∠ABE=∠CBF.
在△ABE和△CBF中,
∵
∴△ABE≌△CBF(SAS),
∴AE=CF.
(2)∵在等边三角形ABC中,AD是∠BAC的平分线,
∴∠BAE=30°,∠ACB=60°.
∵△ABE≌△CBF,
∴∠BCF=∠BAE=30°,
∴∠ACF=∠BCF+∠ACB=30°+60°=90°.
8.解:(1)∠DAC的度数不会改变.理由:
∵EA=EC,
∴∠CAE=∠C.
∵BA=BD,
∴∠BAD=∠BDA.
∵∠BAE=90°,
∴∠B=90°-∠AED=90°-2∠C,
∴∠BAD=(180°-∠B)=[180°-(90°-2∠C)]=45°+∠C,
∴∠DAE=90°-∠BAD=90°-(45°+∠C)=45°-∠C,
∴∠DAC=∠DAE+∠CAE=45°-∠C+∠C=45°.
(2)设∠ABC=m°,则∠BAD=(180°-m°)=90°-m°,∠AEB=180°-n°-m°,
∴∠DAE=n°-∠BAD=n°-90°+m°.
∵EA=EC,
∴∠CAE=∠AEB=90°-n°-m°,
∴∠DAC=∠DAE+∠CAE=n°-90°+m°+90°-n°-m°=n°.
9.B [解析] 过点D作DH⊥AB交BA的延长线于点H.
∵BD平分∠ABC,∠BCD=90°,
∴DH=CD=4,
∴四边形ABCD的面积=S△ABD+S△BCD=AB·DH+BC·CD=×6×4+×9×4=30.
10.B [解析] 过点C作CE⊥AB于点E,交BD于点M',过点M'作M'N'⊥BC于点N'.
∵BD平分∠ABC,M'E⊥AB于点E,M'N'⊥BC于点N',
∴M'N'=M'E,∴CE=CM'+M'E=CM'+M'N',
∴当点M与点M'重合,点N与点N'重合时,CM+MN的值最小.
∵△ABC的面积为8,AB=4,
∴×4·CE=8,
∴CE=4,
即CM+MN的最小值为4.
11.解:(1)猜想:AB=AC+CD.
(2)猜想:AB+AC=CD.
证明:在BA的延长线上截取AE=AC,连接ED.
∵AD平分∠FAC,
∴∠EAD=∠CAD.
在△EAD与△CAD中,
∵
∴△EAD≌△CAD.
∴ED=CD,∠AED=∠ACD.
∴∠FED=∠ACB.
又∵∠ACB=2∠B,∠FED=∠B+∠EDB,
∴∠EDB=∠B.
∴EB=ED.
∴AE+AB=EB=ED=CD.
∴AB+AC=CD.
