2021—2022学年人教版(2012)七年级下册数学5.2 平行线及其判定 导学案(含2课时,无答案)
文档属性
| 名称 | 2021—2022学年人教版(2012)七年级下册数学5.2 平行线及其判定 导学案(含2课时,无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 770.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 00:00:00 | ||
图片预览

文档简介
5.2平行线及其判定
【课时安排】
2课时
【第一课时】
【学习目标】
1.掌握平行线的三种判定方法,能运用平行线的判定方法解决问题。
2.通过独立思考,小组探究,理解角与线的位置关系之间的联系,体会数形结合思想。
3.激情投入,善于发现问题和提出问题,感受学习数学的乐趣。
【学习重点】
三种判定方法判定两直线平行。
【学习难点】
根据平行线的判定方法进行简单的推理。
【学习过程】
一、知识链接
1.在同一平面内,_____的两条直线叫做平行线。
2.过已知直线外一点能且只能画_____条直线与这条直线垂直,能且只能画_____条直线与这条直线平行。
3.同位角、内错角、同旁内角的定义是怎样叙述的?
4.怎样用三角板和直尺作已知直线的平行线?
二、新知预习
1.试利用三角板和直尺,经过直线外一点P画出已知直线AB的平行线CD,由此你会发现什么?
2.同位角_____,两直线平行。
三、自学自测
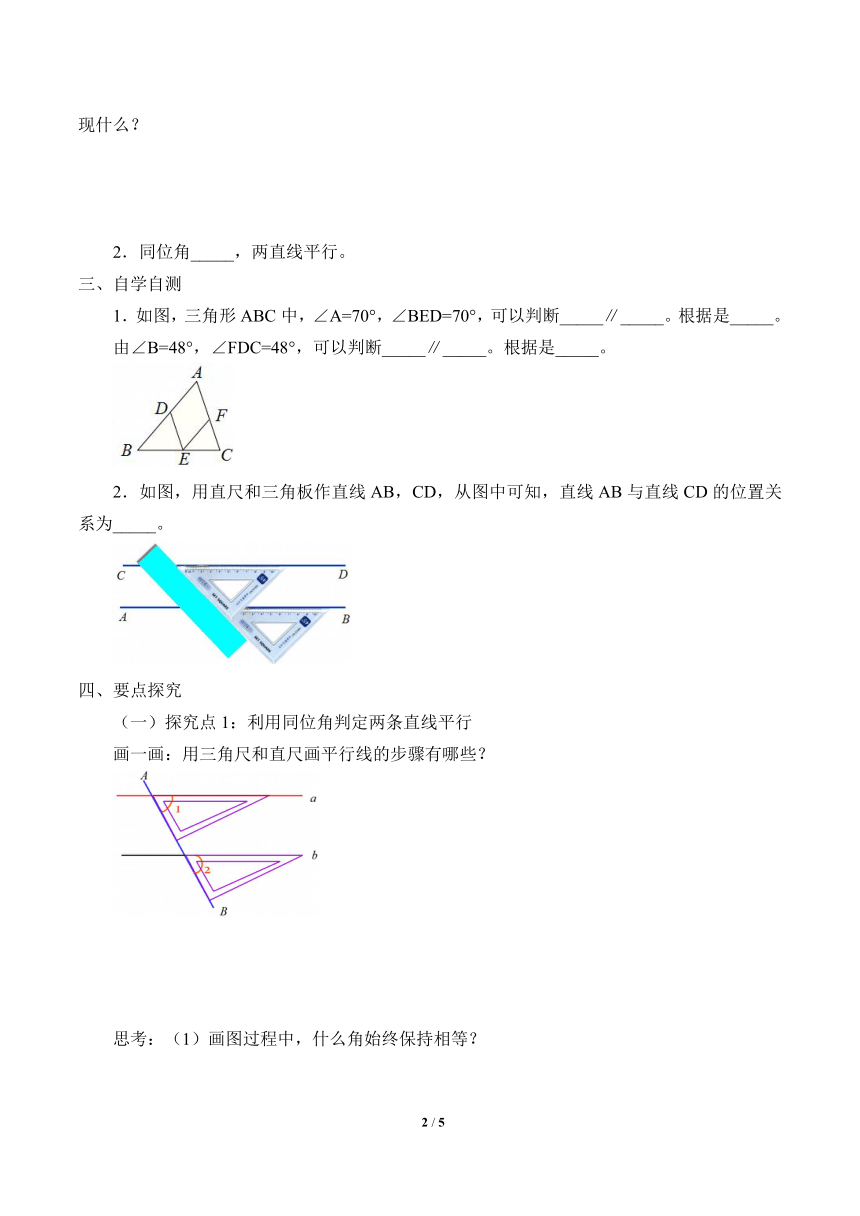
1.如图,三角形ABC中,∠A=70°,∠BED=70°,可以判断_____∥_____。根据是_____。
由∠B=48°,∠FDC=48°,可以判断_____∥_____。根据是_____。
2.如图,用直尺和三角板作直线AB,CD,从图中可知,直线AB与直线CD的位置关系为_____。
四、要点探究
(一)探究点1:利用同位角判定两条直线平行
画一画:用三角尺和直尺画平行线的步骤有哪些?
思考:(1)画图过程中,什么角始终保持相等?
(2)直线a,b位置关系如何?
(3)由上面的操作过程,你能发现判定两直线平行的方法吗?
总结归纳:
判定方法1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
简单说成:同位角相等,两直线平行。
应用格式: ∵∠1=∠2(已知),∴a∥b(同位角相等,两直线平行)
(二)探究点2:利用内错角、同旁内角判定两条直线平行
问题1:如图,由∠3=∠2,可推出a//b吗?如何推出?
总结归纳:
判定方法2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。
简单说成:内错角相等,两直线平行。
应用格式:∵∠3=∠2(已知),∴a∥b(内错角相等,两直线平行)
问题2:如图,如果∠1+∠2=180°,你能判定a//b吗?
总结归纳:
判定方法3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。
简单说成:同旁内角互补,两直线平行。
应用格式:∵∠1+∠2=180°(已知),∴a∥b(同旁内角互补,两直线平行)
五、课堂小结
文字叙述 符号语言 图形
_____相等, 两直线平行 ∵_____(已知), ∴a∥b
_____相等, 两直线平行 ∵_____(已知), ∴a∥b
_____互补, 两直线平行 ∵_____(已知) ∴a∥b
【第二课时】
【学习目标】
1.进一步掌握平行线的判定方法,并会运用平行线的判定解决问题。
2.握垂直于同一条直线的两条直线互相平行。
【学习重点】
平行线的判定方法。
【学习难点】
熟练运用平行线的判定方法解决问题。
【学习过程】
一、知识链接
什么叫平行线?平行线的判定方法有哪些?
二、要点归纳:
垂直于同一条直线的两条直线_____。
三、要点探究
(一)探究点1:平行线的判定的综合运用
(二)探究点2:在同一平面内,垂直于同一条直线的两条直线平行
问题:在同一平面内,两条直线垂直于同一条直线,这两条直线平行吗?为什么?
猜想:垂直于同一条直线的两条直线平行。
验证猜想:如图,在同一平面内,b⊥a,c⊥a,试说明:b∥C.
解:
四、课堂小结
判断两直线平行的方法 几何语言 图示
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
平行于同一直线的两直线平行
同一平面内,垂直于同一直线的两直线平行
平行线的定义
1 / 5
【课时安排】
2课时
【第一课时】
【学习目标】
1.掌握平行线的三种判定方法,能运用平行线的判定方法解决问题。
2.通过独立思考,小组探究,理解角与线的位置关系之间的联系,体会数形结合思想。
3.激情投入,善于发现问题和提出问题,感受学习数学的乐趣。
【学习重点】
三种判定方法判定两直线平行。
【学习难点】
根据平行线的判定方法进行简单的推理。
【学习过程】
一、知识链接
1.在同一平面内,_____的两条直线叫做平行线。
2.过已知直线外一点能且只能画_____条直线与这条直线垂直,能且只能画_____条直线与这条直线平行。
3.同位角、内错角、同旁内角的定义是怎样叙述的?
4.怎样用三角板和直尺作已知直线的平行线?
二、新知预习
1.试利用三角板和直尺,经过直线外一点P画出已知直线AB的平行线CD,由此你会发现什么?
2.同位角_____,两直线平行。
三、自学自测
1.如图,三角形ABC中,∠A=70°,∠BED=70°,可以判断_____∥_____。根据是_____。
由∠B=48°,∠FDC=48°,可以判断_____∥_____。根据是_____。
2.如图,用直尺和三角板作直线AB,CD,从图中可知,直线AB与直线CD的位置关系为_____。
四、要点探究
(一)探究点1:利用同位角判定两条直线平行
画一画:用三角尺和直尺画平行线的步骤有哪些?
思考:(1)画图过程中,什么角始终保持相等?
(2)直线a,b位置关系如何?
(3)由上面的操作过程,你能发现判定两直线平行的方法吗?
总结归纳:
判定方法1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
简单说成:同位角相等,两直线平行。
应用格式: ∵∠1=∠2(已知),∴a∥b(同位角相等,两直线平行)
(二)探究点2:利用内错角、同旁内角判定两条直线平行
问题1:如图,由∠3=∠2,可推出a//b吗?如何推出?
总结归纳:
判定方法2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。
简单说成:内错角相等,两直线平行。
应用格式:∵∠3=∠2(已知),∴a∥b(内错角相等,两直线平行)
问题2:如图,如果∠1+∠2=180°,你能判定a//b吗?
总结归纳:
判定方法3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。
简单说成:同旁内角互补,两直线平行。
应用格式:∵∠1+∠2=180°(已知),∴a∥b(同旁内角互补,两直线平行)
五、课堂小结
文字叙述 符号语言 图形
_____相等, 两直线平行 ∵_____(已知), ∴a∥b
_____相等, 两直线平行 ∵_____(已知), ∴a∥b
_____互补, 两直线平行 ∵_____(已知) ∴a∥b
【第二课时】
【学习目标】
1.进一步掌握平行线的判定方法,并会运用平行线的判定解决问题。
2.握垂直于同一条直线的两条直线互相平行。
【学习重点】
平行线的判定方法。
【学习难点】
熟练运用平行线的判定方法解决问题。
【学习过程】
一、知识链接
什么叫平行线?平行线的判定方法有哪些?
二、要点归纳:
垂直于同一条直线的两条直线_____。
三、要点探究
(一)探究点1:平行线的判定的综合运用
(二)探究点2:在同一平面内,垂直于同一条直线的两条直线平行
问题:在同一平面内,两条直线垂直于同一条直线,这两条直线平行吗?为什么?
猜想:垂直于同一条直线的两条直线平行。
验证猜想:如图,在同一平面内,b⊥a,c⊥a,试说明:b∥C.
解:
四、课堂小结
判断两直线平行的方法 几何语言 图示
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
平行于同一直线的两直线平行
同一平面内,垂直于同一直线的两直线平行
平行线的定义
1 / 5
