沪科版七年级上册1.6.1 有理数的乘方课件(共23张PPT)
文档属性
| 名称 | 沪科版七年级上册1.6.1 有理数的乘方课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 00:00:00 | ||
图片预览


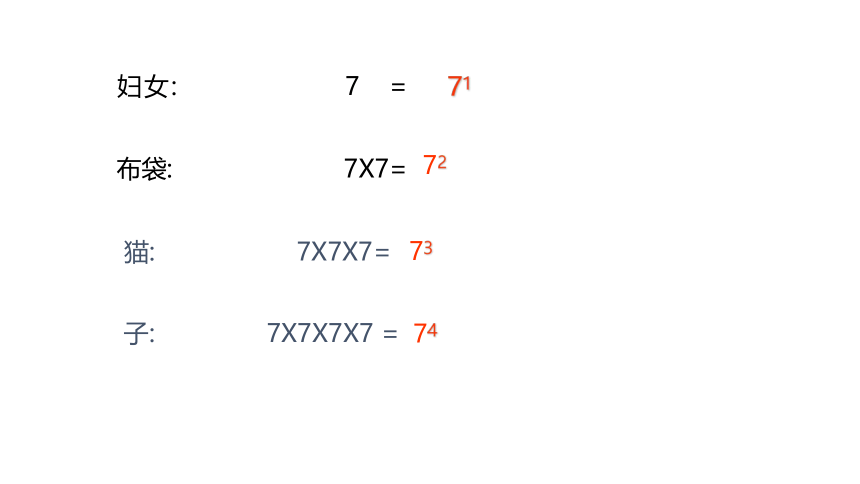
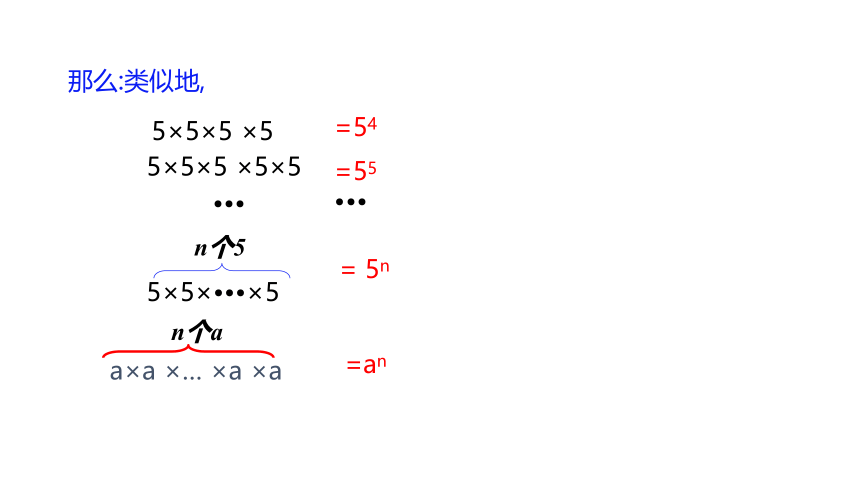



文档简介
(共23张PPT)
第一章 有理数
1.6.1 有理数的乘方
情景导入
中世纪意大利数学家斐波那契在《算盘全书》里记载了一首歌谣:
我赴圣地爱弗西,途遇妇女数有七,一人七袋手中提,一袋七猫数整齐,一猫七子紧相依,妇与布袋猫与子,几何同时赴圣地
猫: 7X7X7=
妇女: 7 =
71
布袋: 7X7=
子: 7X7X7X7 =
72
73
74
获取新知
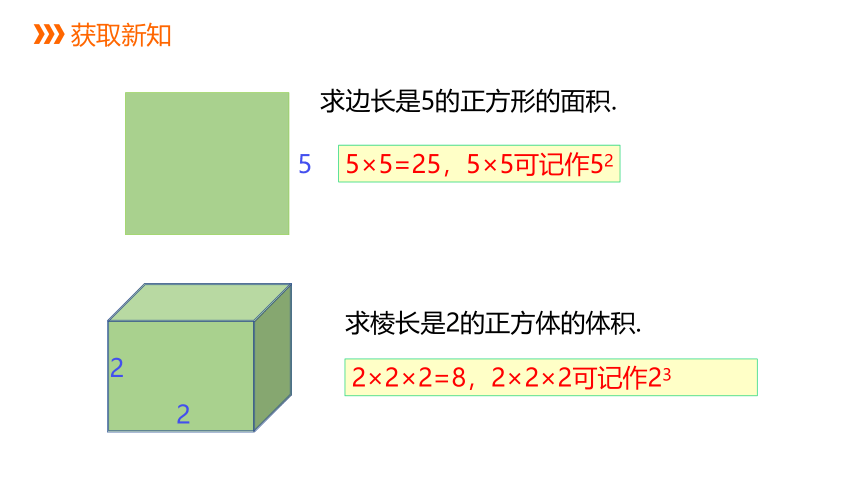
求边长是5的正方形的面积.
5
5×5=25,5×5可记作52
2
2
2×2×2=8,2×2×2可记作23
求棱长是2的正方体的体积.
那么:类似地,
5×5×5 ×5
5×5×5 ×5×5
5×5× ×5
n个5
=54
=55
= 5n
a×a ×… ×a ×a
n个a
=an
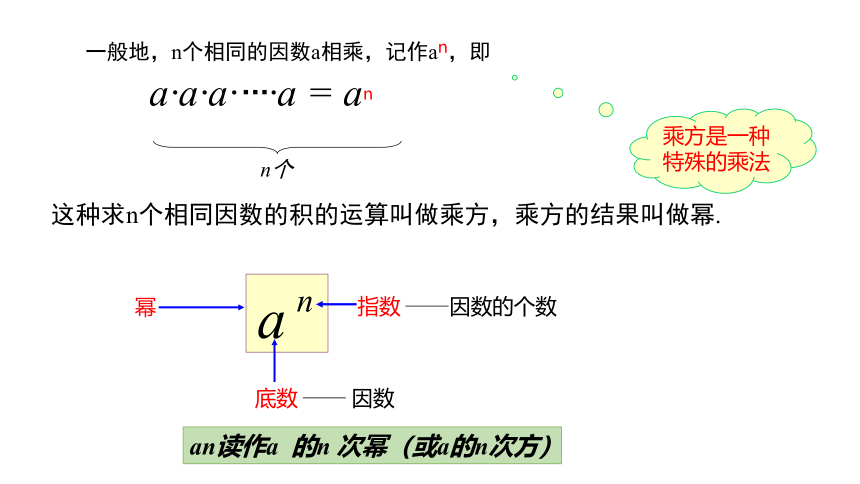
一般地,n个相同的因数a相乘,记作an,即
a·a·a· ·a = an
n个
…
乘方是一种特殊的乘法
幂
指数
因数的个数
底数
因数
这种求n个相同因数的积的运算叫做乘方,乘方的结果叫做幂.
an读作a 的n 次幂(或a的n次方)
例如:
在幂52中,读作“5的平方”(或“5的2次方”或“5的2次幂”),
底数是5,指数是2,
(-3)×(-3)×(-3) ×(-3)记作(-3)4,读作“-3的4次方”或“-3的4次幂”,底数是(-3),指数是4
底数是 ,指数是5
备注:当底数是分数或负数时,要加括号.
例1 利用乘方的意义计算:
(3) 09=0.
思考:你发现正数的幂的正负有什么规律?0的幂呢?
解:(1) 53=5×5×5=125;
正数的任何次幂都是正数,0的任何正整数次幂都是0.
例题讲解
例2 计算:
(1) (-4)3; (2) (-2)4; (3)
解:(1) (-4)3=(-4)×(-4)×(-4)=-64;
(2) (-2)4=(-2)×(-2)×(-2)×(-2)=16;
观察上述运算结果,你发现负数的幂的正负有什么规律?
负数的奇次幂是负数,负数的偶次幂是正数.
(1)
(2)
正数的任何次幂都是正数;
负数的
偶次幂是正数
奇次幂是负数
0的任何正整数次幂都是0
(3)
奇负偶正
幂的符号法则
例3 说说下列各数的意义,它们一样吗
解:(-3)4底数是-3,指数是4
(-3)4的意义是4个-3相乘,结果是81
-34底数是3,指数是4
-34的意义是3的4次方的相反数,结果是-81
底数是 ,指数是2,
意义是2个 相乘,结果是
底数是 2 ,指数是2 ,
意义是2的平方再除以3,结果是
(-3)4和-34
获取新知
思考:上式含有哪几种运算 先算什么,后算什么?
加减运算
乘方运算
第一级运算
第三级运算
乘除运算
第二级运算
含有有理数的加、减、乘、除及乘方的运算叫做有理数的混合运算.
有理数的运算级别:
级 别
名 称
第一级运算
加、减
第二级运算
乘、除
第三级运算
乘方(还有今后学的开方)
①先乘方,再乘除,最后加减;
②同级运算,从左到右进行;
③如果有括号,先算括号内的运算,
按小括号、中括号、大括号依次进行.
例4 计算:
(1)-10+8÷(-2)2-(-4)×(-3);
(2)
解:
(1) -10+8÷(-2)2-(-4)×(-3)
= -10+8÷4-4×3
=-10+2-12
=-20.
例5 计算:
解:原式
备注:进行有理数的混合运算时,一定要按运算顺序进行计算,并且能够正确运用运算律.
2.计算6×(-2)-12÷(-4)的结果是( )
A.10 B.0 C.-3 D.-9
随堂演练
1.(-3)2计算的结果是( )
A.-6 B.6
C.-9 D.9
D
D
3.下列等式成立的是( )
A.(-3)2=-32 B.-23=(-2)3
C. 23=(-2)3 D. 32=-32
B
4.计算 的结果是( )
A.-2 B.2 C.0 D.-1
C
5.(1)(-5)2的底数是_____,指数是_____,(-5)2表示2个_____相乘,读作_____的2次方,也读作-5的_____.
(2) 表示 个 相乘,读作 的 次方,也读作 的 次幂,其中 叫做 ,6叫做 .
-5
2
-5
-5
平方
6
6
底数
指数
6
6. 计算(1)
(2)-23×(-32)
(3)64÷(-2)5
(4)(-4)3÷(-1)200+2×(-3)4
(2)-23×(-32)=-8×(-9)=72;
(3)64÷(-2)5=64÷(-32)=-2;
(4)(-4)3÷(-1)200+2×(-3)4=-64÷1+2×81=98
7.计算
(2)原式
解:(1)原式=
1×2+(-8)÷4
=2+(-2)
=0
(3)原式
8.珠穆朗玛峰是世界的最高峰,它的海拔高度是8844米.把一张足够大的厚度为0.1毫米的纸,连续对折30次的厚度能超过珠穆朗玛峰,这是真的吗?
解:折纸次数 纸的厚度(毫米)
1 0.1×2
2 0.1×2×2
3 0.1×2×2×2
…
30 0.1×2×2×···×2
=0.1×22
=0.1×23
30个2
=0.1×230
0.1×230=0.1×1073741824毫米
=107374.1824米
>8848米
课堂小结
乘方的符号法则:
1.正数的任何次幂都是正数
2.负数的奇次幂是负数,负数的偶次幂是正数
3.零的正整数次幂都是零
幂
指数
底数
乘方
定义
求几个相同因数的积的运算
先算乘方,再算乘除,最后算加减,如有括号,先进行括号里的运算.
有理数混合
运算顺序
第一章 有理数
1.6.1 有理数的乘方
情景导入
中世纪意大利数学家斐波那契在《算盘全书》里记载了一首歌谣:
我赴圣地爱弗西,途遇妇女数有七,一人七袋手中提,一袋七猫数整齐,一猫七子紧相依,妇与布袋猫与子,几何同时赴圣地
猫: 7X7X7=
妇女: 7 =
71
布袋: 7X7=
子: 7X7X7X7 =
72
73
74
获取新知
求边长是5的正方形的面积.
5
5×5=25,5×5可记作52
2
2
2×2×2=8,2×2×2可记作23
求棱长是2的正方体的体积.
那么:类似地,
5×5×5 ×5
5×5×5 ×5×5
5×5× ×5
n个5
=54
=55
= 5n
a×a ×… ×a ×a
n个a
=an
一般地,n个相同的因数a相乘,记作an,即
a·a·a· ·a = an
n个
…
乘方是一种特殊的乘法
幂
指数
因数的个数
底数
因数
这种求n个相同因数的积的运算叫做乘方,乘方的结果叫做幂.
an读作a 的n 次幂(或a的n次方)
例如:
在幂52中,读作“5的平方”(或“5的2次方”或“5的2次幂”),
底数是5,指数是2,
(-3)×(-3)×(-3) ×(-3)记作(-3)4,读作“-3的4次方”或“-3的4次幂”,底数是(-3),指数是4
底数是 ,指数是5
备注:当底数是分数或负数时,要加括号.
例1 利用乘方的意义计算:
(3) 09=0.
思考:你发现正数的幂的正负有什么规律?0的幂呢?
解:(1) 53=5×5×5=125;
正数的任何次幂都是正数,0的任何正整数次幂都是0.
例题讲解
例2 计算:
(1) (-4)3; (2) (-2)4; (3)
解:(1) (-4)3=(-4)×(-4)×(-4)=-64;
(2) (-2)4=(-2)×(-2)×(-2)×(-2)=16;
观察上述运算结果,你发现负数的幂的正负有什么规律?
负数的奇次幂是负数,负数的偶次幂是正数.
(1)
(2)
正数的任何次幂都是正数;
负数的
偶次幂是正数
奇次幂是负数
0的任何正整数次幂都是0
(3)
奇负偶正
幂的符号法则
例3 说说下列各数的意义,它们一样吗
解:(-3)4底数是-3,指数是4
(-3)4的意义是4个-3相乘,结果是81
-34底数是3,指数是4
-34的意义是3的4次方的相反数,结果是-81
底数是 ,指数是2,
意义是2个 相乘,结果是
底数是 2 ,指数是2 ,
意义是2的平方再除以3,结果是
(-3)4和-34
获取新知
思考:上式含有哪几种运算 先算什么,后算什么?
加减运算
乘方运算
第一级运算
第三级运算
乘除运算
第二级运算
含有有理数的加、减、乘、除及乘方的运算叫做有理数的混合运算.
有理数的运算级别:
级 别
名 称
第一级运算
加、减
第二级运算
乘、除
第三级运算
乘方(还有今后学的开方)
①先乘方,再乘除,最后加减;
②同级运算,从左到右进行;
③如果有括号,先算括号内的运算,
按小括号、中括号、大括号依次进行.
例4 计算:
(1)-10+8÷(-2)2-(-4)×(-3);
(2)
解:
(1) -10+8÷(-2)2-(-4)×(-3)
= -10+8÷4-4×3
=-10+2-12
=-20.
例5 计算:
解:原式
备注:进行有理数的混合运算时,一定要按运算顺序进行计算,并且能够正确运用运算律.
2.计算6×(-2)-12÷(-4)的结果是( )
A.10 B.0 C.-3 D.-9
随堂演练
1.(-3)2计算的结果是( )
A.-6 B.6
C.-9 D.9
D
D
3.下列等式成立的是( )
A.(-3)2=-32 B.-23=(-2)3
C. 23=(-2)3 D. 32=-32
B
4.计算 的结果是( )
A.-2 B.2 C.0 D.-1
C
5.(1)(-5)2的底数是_____,指数是_____,(-5)2表示2个_____相乘,读作_____的2次方,也读作-5的_____.
(2) 表示 个 相乘,读作 的 次方,也读作 的 次幂,其中 叫做 ,6叫做 .
-5
2
-5
-5
平方
6
6
底数
指数
6
6. 计算(1)
(2)-23×(-32)
(3)64÷(-2)5
(4)(-4)3÷(-1)200+2×(-3)4
(2)-23×(-32)=-8×(-9)=72;
(3)64÷(-2)5=64÷(-32)=-2;
(4)(-4)3÷(-1)200+2×(-3)4=-64÷1+2×81=98
7.计算
(2)原式
解:(1)原式=
1×2+(-8)÷4
=2+(-2)
=0
(3)原式
8.珠穆朗玛峰是世界的最高峰,它的海拔高度是8844米.把一张足够大的厚度为0.1毫米的纸,连续对折30次的厚度能超过珠穆朗玛峰,这是真的吗?
解:折纸次数 纸的厚度(毫米)
1 0.1×2
2 0.1×2×2
3 0.1×2×2×2
…
30 0.1×2×2×···×2
=0.1×22
=0.1×23
30个2
=0.1×230
0.1×230=0.1×1073741824毫米
=107374.1824米
>8848米
课堂小结
乘方的符号法则:
1.正数的任何次幂都是正数
2.负数的奇次幂是负数,负数的偶次幂是正数
3.零的正整数次幂都是零
幂
指数
底数
乘方
定义
求几个相同因数的积的运算
先算乘方,再算乘除,最后算加减,如有括号,先进行括号里的运算.
有理数混合
运算顺序
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
