20.3菱形的性质 课件
图片预览









文档简介
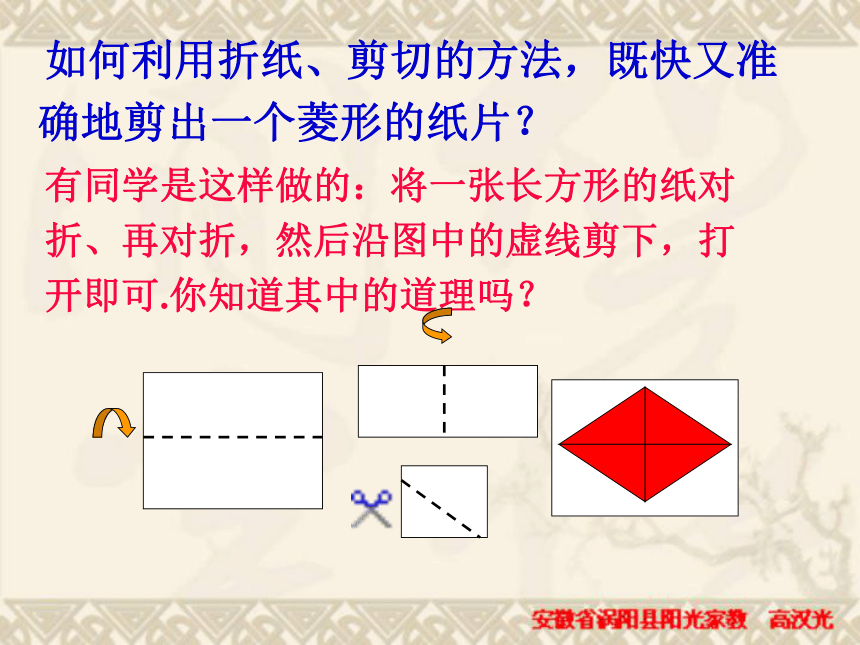
课件36张PPT。 菱形的性质 矩形的概念及性质矩形:有一个角是直角的特殊平行四边形。矩形的性质:矩形的对角线相等且互相平分。 矩形具有平行四边形的所有性质 ;矩形的四个内角都是直角;矩形既是轴对称图形又是中心对称图形 ;平行四边形的对边平行且相等;平行线之间的距离处处相等平行四边形的概念及性质平行四边形的对角相等、邻角互补;平行四边形的对角线互相平分 ;平行四边形是中心对称图形 .美观别致的“菱形”菱形就在我们身边一组邻边相等的平行四边形叫做菱形.一组邻边相等有一组邻边相等的平行四边形叫做菱形菱形的定义菱形记一记有同学是这样做的:将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可.你知道其中的道理吗? 如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?菱形是轴对称图形探究菱形的性质(2)从图中你能得到哪些结论?并说明理由.提示:从边、角、对角线、面积等方面来探讨 (1)观察得到的菱形,它是中心对称图形吗?
它是轴对称图形吗?如果是,有几条对称轴?
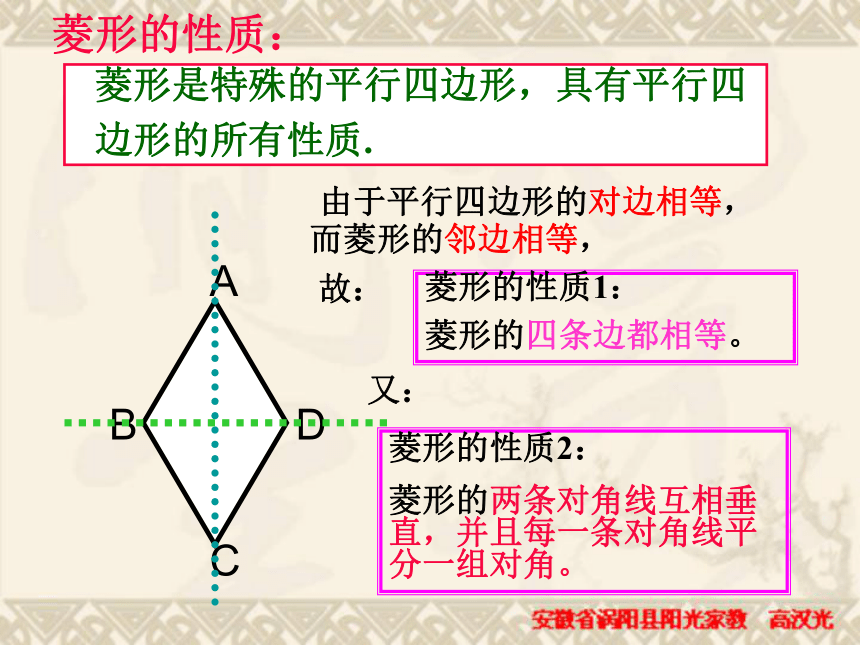
对称轴之间有什么位置关系?菱形是中心对称图形 由于平行四边形的对边相等,而菱形的邻边相等,
故:菱形的性质2:
菱形的两条对角线互相垂直,并且每一条对角线平分一组对角。菱形是特殊的平行四边形,具有平行四
边形的所有性质.菱形的性质:菱形的性质1:
菱形的四条边都相等。又:已知:菱形ABCD的对角线AC和BD相交于点O,如下图,证明:∵四边形ABCD是菱形在△ABD中,
又∵BO=DO∴AB=AD(菱形的四条边都相等)∴AC⊥BD,AC平分∠BAD同理: AC平分∠BCD;
BD平分∠ABC和∠ADC
求证:AC⊥BD ;
AC平分∠BAD和∠BCD ;BD平分∠ABC和∠ADC 命题:菱形的对角线互相垂直平分,
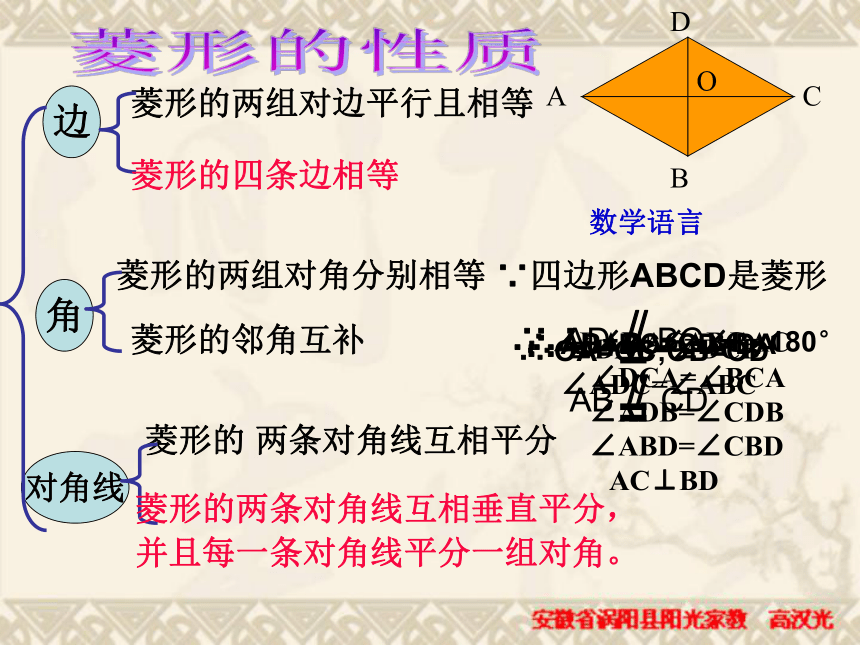
并且每一条对角线平分一组对角;菱形的 两条对角线互相平分菱形的两组对边平行且相等边对角线角数学语言菱形的性质菱形的四条边相等菱形的两组对角分别相等菱形的邻角互补菱形的两条对角线互相垂直平分,
并且每一条对角线平分一组对角。∵四边形ABCD是菱形 ∴ AB=BC=CD=DA∴ ∠DAC=∠BAC
∠DCA=∠BCA
∠ADB=∠CDB
∠ABD=∠CBD
AC⊥BD ∴ OA=OC;OB=OD∴ ∠DAB=∠DCB
∠ADC=∠ABC ∴ ∠DAB+∠ABC= 180° 【菱形的面积公式】OES菱形=BC. AE思考:计算菱形的面积除了上式方法外,利用对角线能 计算菱形的面积公式吗? 面积:S菱形=底×高=对角线乘积的一半如图,在菱形ABCD中,对角线AC、BD相交于点O(2)有哪些特殊的三角形?(1)图中有哪些线段是相等的?哪些角是相 等的?议一议相等的线段:相等的角:等腰三角形:直角三角形:全等三角形:已知四边形ABCD是菱形AB=CD=AD=BC
OA=OC OB=OD∠DAB=∠BCD ∠ABC =∠CDA
∠AOB=∠DOC=∠AOD=∠BOC =90°
∠1=∠2=∠3=∠4 ∠5=∠6=∠7=∠8△ABC △ DBC △ACD △ABDRt△AOB Rt△BOC Rt△COD Rt△DOARt△AOB ≌ Rt△BOC≌ Rt△COD ≌ Rt△DOA
△ABD≌△BCD △ABC≌△ACDABCDO12345678例1:四边形ABCD是菱形,O是两条对角线的交点,已知AB=5cm,AO=4cm,求对角线BD的长。解:∵四边形ABCD是菱形∴AC⊥BD∴∴OB=3∴ BD=2OB=6 cm543有关菱形问题可转化为直角三角形或等腰三角形的问题来解决∵AC=10,BD=6= AC·(BO+DO)例2:如图,已知菱形ABCD中,对角线AC=10,BD=6,请你求出这个菱形的面积。解:在菱形ABCD中,AC⊥BD,BO=DO∴S菱形ABCD=S△ABC+ S△ADC = AC·BO+ AC·DOS菱形= a·b(a、b为对角线长)∴S菱形ABCD= ×10×6=30菱形的面积等于两条对角线长的乘积的一半。= AC·BD(菱形的对角线互相垂直平分)例3:已知:如图,四边形ABCD是边长为13cm的菱形,其中对角线BD长10cm.求:(1).对角线AC的长度;
(2).菱形的面积解:(1)∵四边形ABCD是菱形,=2×△ABD的面积∴∠AED=900,(2)菱形ABCD的面积=△ABD的面积+△CBD的面积∴AC=2AE=2×12=24(cm).例4: 如图,在菱形ABCD中,∠BAD=2∠B,试求出∠B的度数,并说明△ABC是等边三角形。(1)在菱形ABCD中,∠B+∠BAD=180o(两直线平行同旁内角互补)又∵∠BAD=2∠B,∴∠B=60o.(2)在菱形ABCD中,解:AB=BC(菱形的四条边都相等)∴在△ABC中,∠BAC=∠BCA(等边对等角)又∵∠B+∠BAC+∠BCA=180o(三角形内角和公式)∴∠BAC=∠BCA=∠B=60o∴AB=BC=AC(等角对等边)即ABC是等边三角形.AD∥BC,例5: 如图,已知菱形ABCD的边长为2cm,∠BAD=120°,对角线AC、BD相交于点O,试求这个菱形的两条对角线AC与BD的长. 解:(1) 在菱形ABCD中,又在△ABC中,AB=BC,∠BAO= ∠BAD= ×120°=60°∴∠BCA=∠BAC=60°(等边对等角),∠ABC=180°-∠BCA-∠BAC=60°,∴△ABC为等边三角形,∴AC=AB=2(cm).(菱形的每一条对角线平分一组对角).∴AB=BC=AC(等角对等边)(2) 在菱形ABCD中,(勾股定理)∴BD=2BO= (cm).例5:如图,已知菱形ABCD的边长为2cm,∠BAD=120°,对角线AC、BD相交于点O,试求这个菱形的两条对角线AC与BD的长. AC⊥BD(菱形的对角线互相垂直),∴ △ AOB为直角三角形,例6:如图,在菱形ABCD中, ∠BAD=2∠B,
试说明ΔABC是等边三角形。ACBD解法一:在菱形ABCD中
∵AD//BC
∴∠B+∠BAD=180°
(两直线平行,同旁内角互补)又∵ ∠BAD=2∠B(已知)
∴ ∠B + 2∠B=180°(等量代换)
∴ ∠B= 60°。
又∵AB=BC(菱形的四条边都相等)
∴ ΔABC是等边三角形
(有一个内角是60°的等腰三角形是等边三角形)例6:如图,在菱形ABCD中, ∠BAD=2∠B,
试说明ΔABC是等边三角形。 解法二:在菱形ABCD中,∠BAD=∠BCD
∵AC 平分∠BAD、∠BCD
(菱形的对角线平分一组内角)
∴∠1=∠2= ∠BADACBD又∵ ∠BAD=2∠B(已知)
∴∠B= ∠BAD(等式的性质)
∴∠1=∠2 =∠B(等量代换) ∴AB=AC=BC(等角对等边)
即ΔABC是等边三角形
(三条边都相等的三角形是等边三角形)12学以致用1.已知菱形的周长是12cm,那么它的边长是______.2.菱形ABCD中∠ABC=60度,则∠BAC=_______.3cm60度3. 菱形的两条对角线长分别为6cm和8cm,则菱形的边长是( )CA.10cm B.7cm C. 5cm D.4cm344.在菱形ABCD中,AE⊥BC,AF⊥CD,E、F分别为BC,CD的中点,那么∠EAF的度数是( )A.75°B.60°C.45°D.30°B5.一个菱形的周长是20cm,它的一个内角
是60°,则此菱形较短对角线的长是_____。6.如图,菱形ABCD的对角线AC=12cm,
BD=16cm,AE⊥BC,求AE的长。ABCDEO5cm解:在菱形ABCD中,AC⊥BD,
OA=OC,OB=OD
∴OA=6cm,OB=8cm
∴AB=BC=10 cm
∵ AE⊥BC
∴ BC×AE= AC×OB
∴AE=9.6 cm学以致用 7. 如图,在菱形ABCD中,AB=5cm, AO=4cm, 求这一菱形的周长与两条对角线的长度。解:这一菱形的周长=4AB=4×5=20cm对角线AC=2AO=2×4=8cm
∵BO=3cm(勾股定理)
∴BD=2BO=2×3=6cm学以致用8. 如图,已知菱形ABCD的一条对角线BD恰好与其边AB的长相等,求这个菱形的各个内角的度数.解:在菱形ABCD中,AD=AB;
∵BD=AB,
∴AD=AB=BD;
∴∠A=∠ADB=∠ABD=60度;
∴∠C=∠A=60度;(菱形对角相等)
∠ABC=∠ADC=2∠ADB
=2×60=120度.(菱形的每一条对角线平分一组对角)学以致用2.已知菱形的两个邻角的比是1:5,高是8cm,则菱形的周长为______1.菱形的面积为24cm2,一条对角线的长为6cm,则另一条对角线长为______;边长为______3.已知菱形的周长为40cm,两对角线的比为3:4,则两对角线的长分别是_______8cm5cm64cm12cm,16cm练习
4.已知菱形ABCD中,对角线AC、BD的长度分别是6cm、8cm,求它的周长和面积. 解:∵在菱形ABCD中,对角线AC、 BD的长度分别是6cm、8cm,
∴OA= AC= ×6=3cm
OB= BD= ×8=4cm
∠AOB=90度
∴AB=5cm (勾股定理)
∴菱形ABCD的周长=4AB=4×5=20cm;
面积= AC×BD= ×6×8=24(平方厘米)
练习5.已知如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AB=1
求(1)∠ABC的度数;
(2)对角线AC、BD的长;
(3)菱形ABCD的面积。练习
6.如图,O是菱形ABCD对角线的交点,作DE∥AC,CE∥BD,DE、CE交于点E,四边形CEDO是矩形吗?说出你的理由。练习 7.菱形ABCD中,对角线AC、BD相交于点O,E、F分别是AB、AD的中点,求证:OE=OF练习 8.如果菱形的一个角是1200,那么这个角的顶点向两条对边所引的两条垂线分别平分两边。练习 9. 如图,边长为a的菱形ABCD中,∠DAB=60度,E是异于A、D两点的动点,F是CD上的动点,满足AE+CF=a。
证明:不论E、F怎样移动,三角形BEF总是正三角形。ABCDEF练习矩形和菱形的性质菱形的面积等于两条对角线长的乘积的一半。
菱形既是轴对称图形,又是中心对称图形。
对称轴是对角线所在的直线,对称中心是两条对角线的交点。
小结两组对边
分别平行矩形有一个角是直角菱形有一组邻边相等1.你的收获是什么?你的困惑是什么?
2.你会用类比的学习方法学习特殊四边形知识吗?
你想知道什么样的四边形就是菱形吗?
四边形反思
它是轴对称图形吗?如果是,有几条对称轴?
对称轴之间有什么位置关系?菱形是中心对称图形 由于平行四边形的对边相等,而菱形的邻边相等,
故:菱形的性质2:
菱形的两条对角线互相垂直,并且每一条对角线平分一组对角。菱形是特殊的平行四边形,具有平行四
边形的所有性质.菱形的性质:菱形的性质1:
菱形的四条边都相等。又:已知:菱形ABCD的对角线AC和BD相交于点O,如下图,证明:∵四边形ABCD是菱形在△ABD中,
又∵BO=DO∴AB=AD(菱形的四条边都相等)∴AC⊥BD,AC平分∠BAD同理: AC平分∠BCD;
BD平分∠ABC和∠ADC
求证:AC⊥BD ;
AC平分∠BAD和∠BCD ;BD平分∠ABC和∠ADC 命题:菱形的对角线互相垂直平分,
并且每一条对角线平分一组对角;菱形的 两条对角线互相平分菱形的两组对边平行且相等边对角线角数学语言菱形的性质菱形的四条边相等菱形的两组对角分别相等菱形的邻角互补菱形的两条对角线互相垂直平分,
并且每一条对角线平分一组对角。∵四边形ABCD是菱形 ∴ AB=BC=CD=DA∴ ∠DAC=∠BAC
∠DCA=∠BCA
∠ADB=∠CDB
∠ABD=∠CBD
AC⊥BD ∴ OA=OC;OB=OD∴ ∠DAB=∠DCB
∠ADC=∠ABC ∴ ∠DAB+∠ABC= 180° 【菱形的面积公式】OES菱形=BC. AE思考:计算菱形的面积除了上式方法外,利用对角线能 计算菱形的面积公式吗? 面积:S菱形=底×高=对角线乘积的一半如图,在菱形ABCD中,对角线AC、BD相交于点O(2)有哪些特殊的三角形?(1)图中有哪些线段是相等的?哪些角是相 等的?议一议相等的线段:相等的角:等腰三角形:直角三角形:全等三角形:已知四边形ABCD是菱形AB=CD=AD=BC
OA=OC OB=OD∠DAB=∠BCD ∠ABC =∠CDA
∠AOB=∠DOC=∠AOD=∠BOC =90°
∠1=∠2=∠3=∠4 ∠5=∠6=∠7=∠8△ABC △ DBC △ACD △ABDRt△AOB Rt△BOC Rt△COD Rt△DOARt△AOB ≌ Rt△BOC≌ Rt△COD ≌ Rt△DOA
△ABD≌△BCD △ABC≌△ACDABCDO12345678例1:四边形ABCD是菱形,O是两条对角线的交点,已知AB=5cm,AO=4cm,求对角线BD的长。解:∵四边形ABCD是菱形∴AC⊥BD∴∴OB=3∴ BD=2OB=6 cm543有关菱形问题可转化为直角三角形或等腰三角形的问题来解决∵AC=10,BD=6= AC·(BO+DO)例2:如图,已知菱形ABCD中,对角线AC=10,BD=6,请你求出这个菱形的面积。解:在菱形ABCD中,AC⊥BD,BO=DO∴S菱形ABCD=S△ABC+ S△ADC = AC·BO+ AC·DOS菱形= a·b(a、b为对角线长)∴S菱形ABCD= ×10×6=30菱形的面积等于两条对角线长的乘积的一半。= AC·BD(菱形的对角线互相垂直平分)例3:已知:如图,四边形ABCD是边长为13cm的菱形,其中对角线BD长10cm.求:(1).对角线AC的长度;
(2).菱形的面积解:(1)∵四边形ABCD是菱形,=2×△ABD的面积∴∠AED=900,(2)菱形ABCD的面积=△ABD的面积+△CBD的面积∴AC=2AE=2×12=24(cm).例4: 如图,在菱形ABCD中,∠BAD=2∠B,试求出∠B的度数,并说明△ABC是等边三角形。(1)在菱形ABCD中,∠B+∠BAD=180o(两直线平行同旁内角互补)又∵∠BAD=2∠B,∴∠B=60o.(2)在菱形ABCD中,解:AB=BC(菱形的四条边都相等)∴在△ABC中,∠BAC=∠BCA(等边对等角)又∵∠B+∠BAC+∠BCA=180o(三角形内角和公式)∴∠BAC=∠BCA=∠B=60o∴AB=BC=AC(等角对等边)即ABC是等边三角形.AD∥BC,例5: 如图,已知菱形ABCD的边长为2cm,∠BAD=120°,对角线AC、BD相交于点O,试求这个菱形的两条对角线AC与BD的长. 解:(1) 在菱形ABCD中,又在△ABC中,AB=BC,∠BAO= ∠BAD= ×120°=60°∴∠BCA=∠BAC=60°(等边对等角),∠ABC=180°-∠BCA-∠BAC=60°,∴△ABC为等边三角形,∴AC=AB=2(cm).(菱形的每一条对角线平分一组对角).∴AB=BC=AC(等角对等边)(2) 在菱形ABCD中,(勾股定理)∴BD=2BO= (cm).例5:如图,已知菱形ABCD的边长为2cm,∠BAD=120°,对角线AC、BD相交于点O,试求这个菱形的两条对角线AC与BD的长. AC⊥BD(菱形的对角线互相垂直),∴ △ AOB为直角三角形,例6:如图,在菱形ABCD中, ∠BAD=2∠B,
试说明ΔABC是等边三角形。ACBD解法一:在菱形ABCD中
∵AD//BC
∴∠B+∠BAD=180°
(两直线平行,同旁内角互补)又∵ ∠BAD=2∠B(已知)
∴ ∠B + 2∠B=180°(等量代换)
∴ ∠B= 60°。
又∵AB=BC(菱形的四条边都相等)
∴ ΔABC是等边三角形
(有一个内角是60°的等腰三角形是等边三角形)例6:如图,在菱形ABCD中, ∠BAD=2∠B,
试说明ΔABC是等边三角形。 解法二:在菱形ABCD中,∠BAD=∠BCD
∵AC 平分∠BAD、∠BCD
(菱形的对角线平分一组内角)
∴∠1=∠2= ∠BADACBD又∵ ∠BAD=2∠B(已知)
∴∠B= ∠BAD(等式的性质)
∴∠1=∠2 =∠B(等量代换) ∴AB=AC=BC(等角对等边)
即ΔABC是等边三角形
(三条边都相等的三角形是等边三角形)12学以致用1.已知菱形的周长是12cm,那么它的边长是______.2.菱形ABCD中∠ABC=60度,则∠BAC=_______.3cm60度3. 菱形的两条对角线长分别为6cm和8cm,则菱形的边长是( )CA.10cm B.7cm C. 5cm D.4cm344.在菱形ABCD中,AE⊥BC,AF⊥CD,E、F分别为BC,CD的中点,那么∠EAF的度数是( )A.75°B.60°C.45°D.30°B5.一个菱形的周长是20cm,它的一个内角
是60°,则此菱形较短对角线的长是_____。6.如图,菱形ABCD的对角线AC=12cm,
BD=16cm,AE⊥BC,求AE的长。ABCDEO5cm解:在菱形ABCD中,AC⊥BD,
OA=OC,OB=OD
∴OA=6cm,OB=8cm
∴AB=BC=10 cm
∵ AE⊥BC
∴ BC×AE= AC×OB
∴AE=9.6 cm学以致用 7. 如图,在菱形ABCD中,AB=5cm, AO=4cm, 求这一菱形的周长与两条对角线的长度。解:这一菱形的周长=4AB=4×5=20cm对角线AC=2AO=2×4=8cm
∵BO=3cm(勾股定理)
∴BD=2BO=2×3=6cm学以致用8. 如图,已知菱形ABCD的一条对角线BD恰好与其边AB的长相等,求这个菱形的各个内角的度数.解:在菱形ABCD中,AD=AB;
∵BD=AB,
∴AD=AB=BD;
∴∠A=∠ADB=∠ABD=60度;
∴∠C=∠A=60度;(菱形对角相等)
∠ABC=∠ADC=2∠ADB
=2×60=120度.(菱形的每一条对角线平分一组对角)学以致用2.已知菱形的两个邻角的比是1:5,高是8cm,则菱形的周长为______1.菱形的面积为24cm2,一条对角线的长为6cm,则另一条对角线长为______;边长为______3.已知菱形的周长为40cm,两对角线的比为3:4,则两对角线的长分别是_______8cm5cm64cm12cm,16cm练习
4.已知菱形ABCD中,对角线AC、BD的长度分别是6cm、8cm,求它的周长和面积. 解:∵在菱形ABCD中,对角线AC、 BD的长度分别是6cm、8cm,
∴OA= AC= ×6=3cm
OB= BD= ×8=4cm
∠AOB=90度
∴AB=5cm (勾股定理)
∴菱形ABCD的周长=4AB=4×5=20cm;
面积= AC×BD= ×6×8=24(平方厘米)
练习5.已知如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AB=1
求(1)∠ABC的度数;
(2)对角线AC、BD的长;
(3)菱形ABCD的面积。练习
6.如图,O是菱形ABCD对角线的交点,作DE∥AC,CE∥BD,DE、CE交于点E,四边形CEDO是矩形吗?说出你的理由。练习 7.菱形ABCD中,对角线AC、BD相交于点O,E、F分别是AB、AD的中点,求证:OE=OF练习 8.如果菱形的一个角是1200,那么这个角的顶点向两条对边所引的两条垂线分别平分两边。练习 9. 如图,边长为a的菱形ABCD中,∠DAB=60度,E是异于A、D两点的动点,F是CD上的动点,满足AE+CF=a。
证明:不论E、F怎样移动,三角形BEF总是正三角形。ABCDEF练习矩形和菱形的性质菱形的面积等于两条对角线长的乘积的一半。
菱形既是轴对称图形,又是中心对称图形。
对称轴是对角线所在的直线,对称中心是两条对角线的交点。
小结两组对边
分别平行矩形有一个角是直角菱形有一组邻边相等1.你的收获是什么?你的困惑是什么?
2.你会用类比的学习方法学习特殊四边形知识吗?
你想知道什么样的四边形就是菱形吗?
四边形反思
