沪科版数学九年级下册同步课时练习:24.7 第2课时 圆锥的侧面积和全面积(word版含答案)
文档属性
| 名称 | 沪科版数学九年级下册同步课时练习:24.7 第2课时 圆锥的侧面积和全面积(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 136.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 00:00:00 | ||
图片预览


文档简介
第2课时 圆锥的侧面积和全面积
知识点 1 圆锥与圆锥的侧面展开图
1.若一个圆锥的侧面展开图是半径为10 cm,圆心角为120°的扇形,则该圆锥的底面半径是 ( )
A. cm B. cm C. cm D. cm
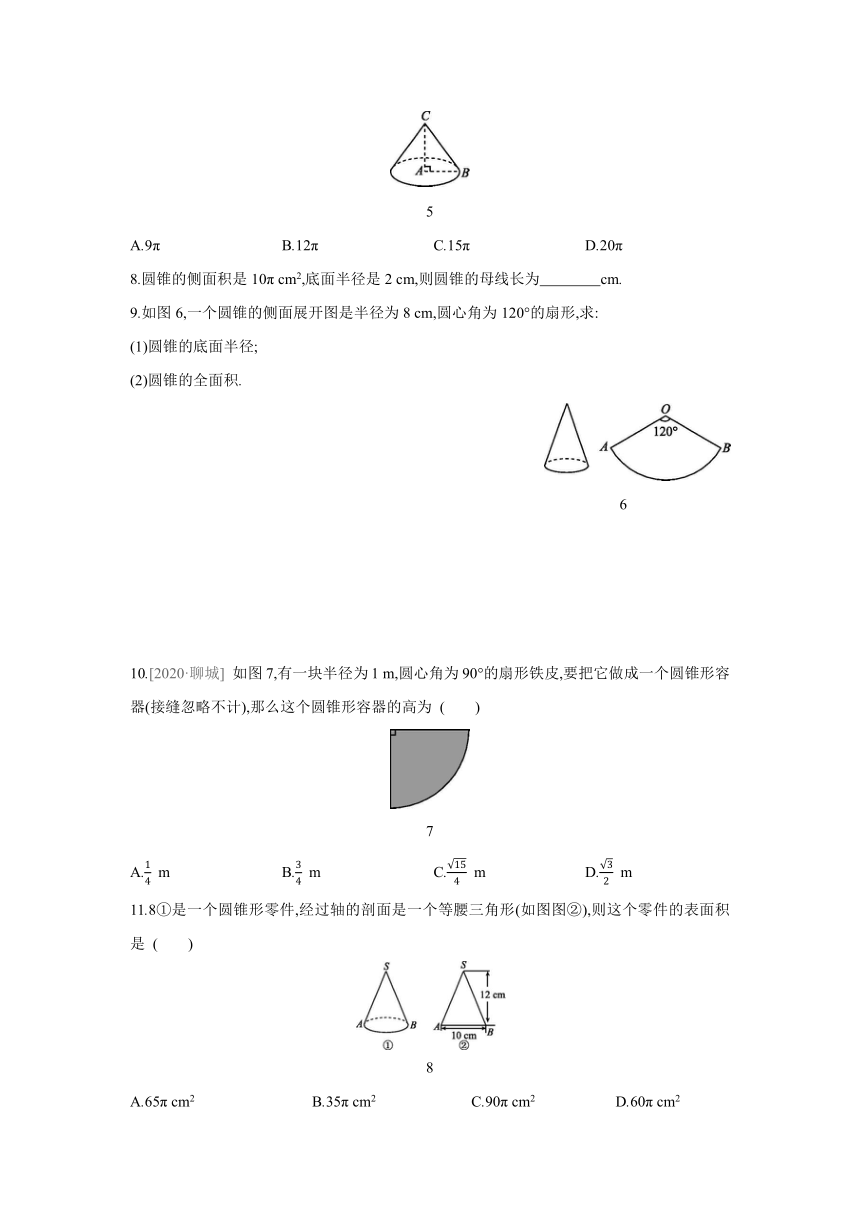
2.如图3,圆锥的底面半径为8,母线长为15,则这个圆锥侧面展开图的扇形的圆心角α为( )
3
A.120° B.150° C.192° D.210°
3.[教材例3变式] 如图4,已知一块圆心角为270°的扇形铁皮,用它做一个圆锥形的烟囱帽(接缝忽略不计),圆锥底面圆的直径是60 cm,则这块扇形铁皮的半径是 ( )
4
A.40 cm B.50 cm C.60 cm D.80 cm
4.如图果圆锥的侧面展开图是半径为6,弧长为4π的扇形,那么这个扇形的圆心角为 .
知识点 2 圆锥的侧面积与全面积
5.[2020·合肥期末] 已知圆锥的底面半径为3 cm,母线长为5 cm,则此圆锥的侧面积是 ( )
A.15π cm2 B.15 cm2
C.20π cm2 D.20 cm2
6.[2020·常德] 一个圆锥的底面半径r=10,高h=20,则这个圆锥的侧面积是 ( )
A.100π B.200π
C.100π D.200π
7.[2020·安庆十四中模拟] 如图5,已知在Rt△ABC中,∠BAC=90°,AC=4,BC=5,若把Rt△ABC绕直线AC旋转一周,则所得圆锥的侧面积等于 ( )
5
A.9π B.12π C.15π D.20π
8.圆锥的侧面积是10π cm2,底面半径是2 cm,则圆锥的母线长为 cm.
9.如图6,一个圆锥的侧面展开图是半径为8 cm,圆心角为120°的扇形,求:
(1)圆锥的底面半径;
(2)圆锥的全面积.
6
10.[2020·聊城] 如图7,有一块半径为1 m,圆心角为90°的扇形铁皮,要把它做成一个圆锥形容器(接缝忽略不计),那么这个圆锥形容器的高为 ( )
7
A. m B. m C. m D. m
11.8①是一个圆锥形零件,经过轴的剖面是一个等腰三角形(如图图②),则这个零件的表面积是 ( )
8
A.65π cm2 B.35π cm2 C.90π cm2 D.60π cm2
12.如图9所示,在矩形纸片ABCD中,AD=6 cm,把它分割成正方形纸片ABFE和矩形纸片EFCD后,分别裁出扇形ABF和半径最大的圆,恰好能作为一个圆锥的侧面和底面,则AB的长为 ( )
9
A.3.5 cm B.4 cm C.4.5 cm D.5 cm
13.如图果一个扇形的弧长等于它的半径,那么此扇形称为“等边扇形”.将半径为5的“等边扇形”围成一个圆锥,则圆锥的侧面积为 .
14.如图0,在Rt△ABC中,∠C=90°,AC=3,BC=4,把它沿斜边AB所在的直线旋转一周,所得几何体的侧面积是 .(结果保留π)
0
15.有一个直径为1 m的圆形铁皮,要从中剪出一个最大的圆心角为90°的扇形BAC,如图1所示.
(1)求被剪掉的阴影部分的面积;
(2)用所留的扇形铁皮围成一个圆锥,则围成的圆锥的底面圆的半径是多少
1
16.如图2,一个圆锥的高为3 cm,侧面展开图是半圆.求:
(1)圆锥的底面半径r与母线R之比;
(2)圆锥的全面积.
2
17.如图3①,在等腰三角形ABC中,AB=AC,当顶角∠A的大小确定时,它的邻边(即腰AB或AC)与对边(即底边BC)的比值也就确定了,我们把这个比值记作T(A),即T(A)==,如图当∠A=60°时,T(60°)=1.
(1)理解巩固:T(90°)= ,T(120°)= ,T(A)的取值范围是 ;
(2)学以致用:如图图②,圆锥的母线长为18,底面直径PQ=14,一只蚂蚁从点P沿着圆锥的侧面爬行到点Q,求蚂蚁爬行的最短路径长(结果保留整数).
(参考数据:T(140°)≈0.53,T(70°)≈0.87,T(35°)≈1.66)
3
答案
1.B 圆锥的侧面展开图是扇形,扇形的弧长==,则圆锥的底面半径=÷2π=(cm).故选B.
2.C 圆锥底面圆的周长=2×8π=16π,∴扇形的圆心角α的度数=圆锥底面周长×180÷15π=192°.故选C.
3.A ∵圆锥底面圆的直径为60 cm,∴圆锥的底面周长为60π cm,∴扇形的弧长为60π cm.设扇形的半径为r,则=60π,解得r=40 cm.故选A.
4.120°
5.A 圆锥的侧面积=2π×3×5÷2=15π(cm2).
故选A.
6.C 这个圆锥的母线长==10,
这个圆锥的侧面积=×2π×10×10=100π.
故选C.
7.C ∵AC=4,BC=5,∴由勾股定理,得AB=3,∴圆锥底面圆的周长是6π,∴圆锥的侧面积为×6π×5=15π.故选C.
8.5 圆锥的底面半径是2 cm,则圆锥的底面周长是4π cm.
设圆锥的母线长是l,则×4πl=10π,
解得l=5.
故答案是5.
9.解:(1)设圆锥的底面半径为r cm.
扇形的弧长==,
∴2πr=,
解得r=,即圆锥的底面半径为 cm.
(2)圆锥的全面积=+π×2= (cm2).
10.C
11.C 根据圆的面积公式,得圆锥的底面积是25π cm2.由勾股定理,知母线==13(cm),∴圆锥的侧面积=×底面周长×母线=65π(cm2),∴圆锥的全面积=65π+25π=90π(cm2).故选C.
12.B =·2π·AB,右侧圆的周长为π·DE.∵恰好能作为一个圆锥的底面和侧面,∴·2π·AB=π·DE,∴AB=2DE,即AE=2DE.∵AE+DE=AD=6,∴AB=AE=4 cm.故选B.
13.12.5 ∵扇形是“等边扇形”,
∴扇形的弧长为5,
∴圆锥的侧面积=×5×5=12.5.
故答案为12.5.
14.π 作CD⊥AB于点D,如图图.
∵∠ACB=90°,AC=3,BC=4,
∴AB==5.
∵CD·AB=AC·BC,
∴CD==.
把Rt△ABC沿斜边AB所在的直线旋转一周,所得几何体为两个圆锥,它们的底面均为以点D为圆心,CD长为半径的圆,
∴这个几何体的侧面积=×2π××3+×2π××4=π.
15.解:(1)如图图,连接BC.
∵∠BAC=90°,
∴BC为☉O的直径,即BC=1 m.
又∵AB=AC,∴AB=BC= m,
∴S阴影部分=S☉O-S扇形ABC=π×2-=(m2).
(2)设底面圆的半径为r,则·2π·=2πr,
∴r= m,∴圆锥的底面圆的半径为 m.
16.解:(1)由题意可知2πr=,
∴R=2r,即r∶R=1∶2.
(2)在Rt△AOC中,∵R2=r2+h2,
∴(2r)2=r2+(3)2,解得r=±3.
∵r>0,∴r=3 cm,R=6 cm,
∴S侧==18π(cm2),S底=πr2=9π(cm2),
∴S全=S侧+S底=18π+9π=27π(cm2).
17.解:(1) T(A)>
(2)∵圆锥的底面直径PQ=14,
∴圆锥的底面周长为14π,
即侧面展开图的扇形的弧长为14π.
设扇形的圆心角为n°,则=14π,
解得n=140.
∵T(70°)≈0.87,
∴蚂蚁爬行的最短路径长为≈21.
知识点 1 圆锥与圆锥的侧面展开图
1.若一个圆锥的侧面展开图是半径为10 cm,圆心角为120°的扇形,则该圆锥的底面半径是 ( )
A. cm B. cm C. cm D. cm
2.如图3,圆锥的底面半径为8,母线长为15,则这个圆锥侧面展开图的扇形的圆心角α为( )
3
A.120° B.150° C.192° D.210°
3.[教材例3变式] 如图4,已知一块圆心角为270°的扇形铁皮,用它做一个圆锥形的烟囱帽(接缝忽略不计),圆锥底面圆的直径是60 cm,则这块扇形铁皮的半径是 ( )
4
A.40 cm B.50 cm C.60 cm D.80 cm
4.如图果圆锥的侧面展开图是半径为6,弧长为4π的扇形,那么这个扇形的圆心角为 .
知识点 2 圆锥的侧面积与全面积
5.[2020·合肥期末] 已知圆锥的底面半径为3 cm,母线长为5 cm,则此圆锥的侧面积是 ( )
A.15π cm2 B.15 cm2
C.20π cm2 D.20 cm2
6.[2020·常德] 一个圆锥的底面半径r=10,高h=20,则这个圆锥的侧面积是 ( )
A.100π B.200π
C.100π D.200π
7.[2020·安庆十四中模拟] 如图5,已知在Rt△ABC中,∠BAC=90°,AC=4,BC=5,若把Rt△ABC绕直线AC旋转一周,则所得圆锥的侧面积等于 ( )
5
A.9π B.12π C.15π D.20π
8.圆锥的侧面积是10π cm2,底面半径是2 cm,则圆锥的母线长为 cm.
9.如图6,一个圆锥的侧面展开图是半径为8 cm,圆心角为120°的扇形,求:
(1)圆锥的底面半径;
(2)圆锥的全面积.
6
10.[2020·聊城] 如图7,有一块半径为1 m,圆心角为90°的扇形铁皮,要把它做成一个圆锥形容器(接缝忽略不计),那么这个圆锥形容器的高为 ( )
7
A. m B. m C. m D. m
11.8①是一个圆锥形零件,经过轴的剖面是一个等腰三角形(如图图②),则这个零件的表面积是 ( )
8
A.65π cm2 B.35π cm2 C.90π cm2 D.60π cm2
12.如图9所示,在矩形纸片ABCD中,AD=6 cm,把它分割成正方形纸片ABFE和矩形纸片EFCD后,分别裁出扇形ABF和半径最大的圆,恰好能作为一个圆锥的侧面和底面,则AB的长为 ( )
9
A.3.5 cm B.4 cm C.4.5 cm D.5 cm
13.如图果一个扇形的弧长等于它的半径,那么此扇形称为“等边扇形”.将半径为5的“等边扇形”围成一个圆锥,则圆锥的侧面积为 .
14.如图0,在Rt△ABC中,∠C=90°,AC=3,BC=4,把它沿斜边AB所在的直线旋转一周,所得几何体的侧面积是 .(结果保留π)
0
15.有一个直径为1 m的圆形铁皮,要从中剪出一个最大的圆心角为90°的扇形BAC,如图1所示.
(1)求被剪掉的阴影部分的面积;
(2)用所留的扇形铁皮围成一个圆锥,则围成的圆锥的底面圆的半径是多少
1
16.如图2,一个圆锥的高为3 cm,侧面展开图是半圆.求:
(1)圆锥的底面半径r与母线R之比;
(2)圆锥的全面积.
2
17.如图3①,在等腰三角形ABC中,AB=AC,当顶角∠A的大小确定时,它的邻边(即腰AB或AC)与对边(即底边BC)的比值也就确定了,我们把这个比值记作T(A),即T(A)==,如图当∠A=60°时,T(60°)=1.
(1)理解巩固:T(90°)= ,T(120°)= ,T(A)的取值范围是 ;
(2)学以致用:如图图②,圆锥的母线长为18,底面直径PQ=14,一只蚂蚁从点P沿着圆锥的侧面爬行到点Q,求蚂蚁爬行的最短路径长(结果保留整数).
(参考数据:T(140°)≈0.53,T(70°)≈0.87,T(35°)≈1.66)
3
答案
1.B 圆锥的侧面展开图是扇形,扇形的弧长==,则圆锥的底面半径=÷2π=(cm).故选B.
2.C 圆锥底面圆的周长=2×8π=16π,∴扇形的圆心角α的度数=圆锥底面周长×180÷15π=192°.故选C.
3.A ∵圆锥底面圆的直径为60 cm,∴圆锥的底面周长为60π cm,∴扇形的弧长为60π cm.设扇形的半径为r,则=60π,解得r=40 cm.故选A.
4.120°
5.A 圆锥的侧面积=2π×3×5÷2=15π(cm2).
故选A.
6.C 这个圆锥的母线长==10,
这个圆锥的侧面积=×2π×10×10=100π.
故选C.
7.C ∵AC=4,BC=5,∴由勾股定理,得AB=3,∴圆锥底面圆的周长是6π,∴圆锥的侧面积为×6π×5=15π.故选C.
8.5 圆锥的底面半径是2 cm,则圆锥的底面周长是4π cm.
设圆锥的母线长是l,则×4πl=10π,
解得l=5.
故答案是5.
9.解:(1)设圆锥的底面半径为r cm.
扇形的弧长==,
∴2πr=,
解得r=,即圆锥的底面半径为 cm.
(2)圆锥的全面积=+π×2= (cm2).
10.C
11.C 根据圆的面积公式,得圆锥的底面积是25π cm2.由勾股定理,知母线==13(cm),∴圆锥的侧面积=×底面周长×母线=65π(cm2),∴圆锥的全面积=65π+25π=90π(cm2).故选C.
12.B =·2π·AB,右侧圆的周长为π·DE.∵恰好能作为一个圆锥的底面和侧面,∴·2π·AB=π·DE,∴AB=2DE,即AE=2DE.∵AE+DE=AD=6,∴AB=AE=4 cm.故选B.
13.12.5 ∵扇形是“等边扇形”,
∴扇形的弧长为5,
∴圆锥的侧面积=×5×5=12.5.
故答案为12.5.
14.π 作CD⊥AB于点D,如图图.
∵∠ACB=90°,AC=3,BC=4,
∴AB==5.
∵CD·AB=AC·BC,
∴CD==.
把Rt△ABC沿斜边AB所在的直线旋转一周,所得几何体为两个圆锥,它们的底面均为以点D为圆心,CD长为半径的圆,
∴这个几何体的侧面积=×2π××3+×2π××4=π.
15.解:(1)如图图,连接BC.
∵∠BAC=90°,
∴BC为☉O的直径,即BC=1 m.
又∵AB=AC,∴AB=BC= m,
∴S阴影部分=S☉O-S扇形ABC=π×2-=(m2).
(2)设底面圆的半径为r,则·2π·=2πr,
∴r= m,∴圆锥的底面圆的半径为 m.
16.解:(1)由题意可知2πr=,
∴R=2r,即r∶R=1∶2.
(2)在Rt△AOC中,∵R2=r2+h2,
∴(2r)2=r2+(3)2,解得r=±3.
∵r>0,∴r=3 cm,R=6 cm,
∴S侧==18π(cm2),S底=πr2=9π(cm2),
∴S全=S侧+S底=18π+9π=27π(cm2).
17.解:(1) T(A)>
(2)∵圆锥的底面直径PQ=14,
∴圆锥的底面周长为14π,
即侧面展开图的扇形的弧长为14π.
设扇形的圆心角为n°,则=14π,
解得n=140.
∵T(70°)≈0.87,
∴蚂蚁爬行的最短路径长为≈21.
