沪科版数学九年级下册同步课时练习:25.2 第2课时 棱柱与三视图(word版含答案)
文档属性
| 名称 | 沪科版数学九年级下册同步课时练习:25.2 第2课时 棱柱与三视图(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 243.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 00:00:00 | ||
图片预览

文档简介
第2课时 棱柱与三视图
知识点 1 棱柱的三视图
1.[2020·眉山] 如图6所示的几何体的主视图为 ( )
6
7
2.8所示的几何体是一个正三棱柱,9中不是其三视图的是 ( )
8
9
3.0所示的正六棱柱的左视图是 ( )
0
1
知识点 2 棱柱的三视图的画法
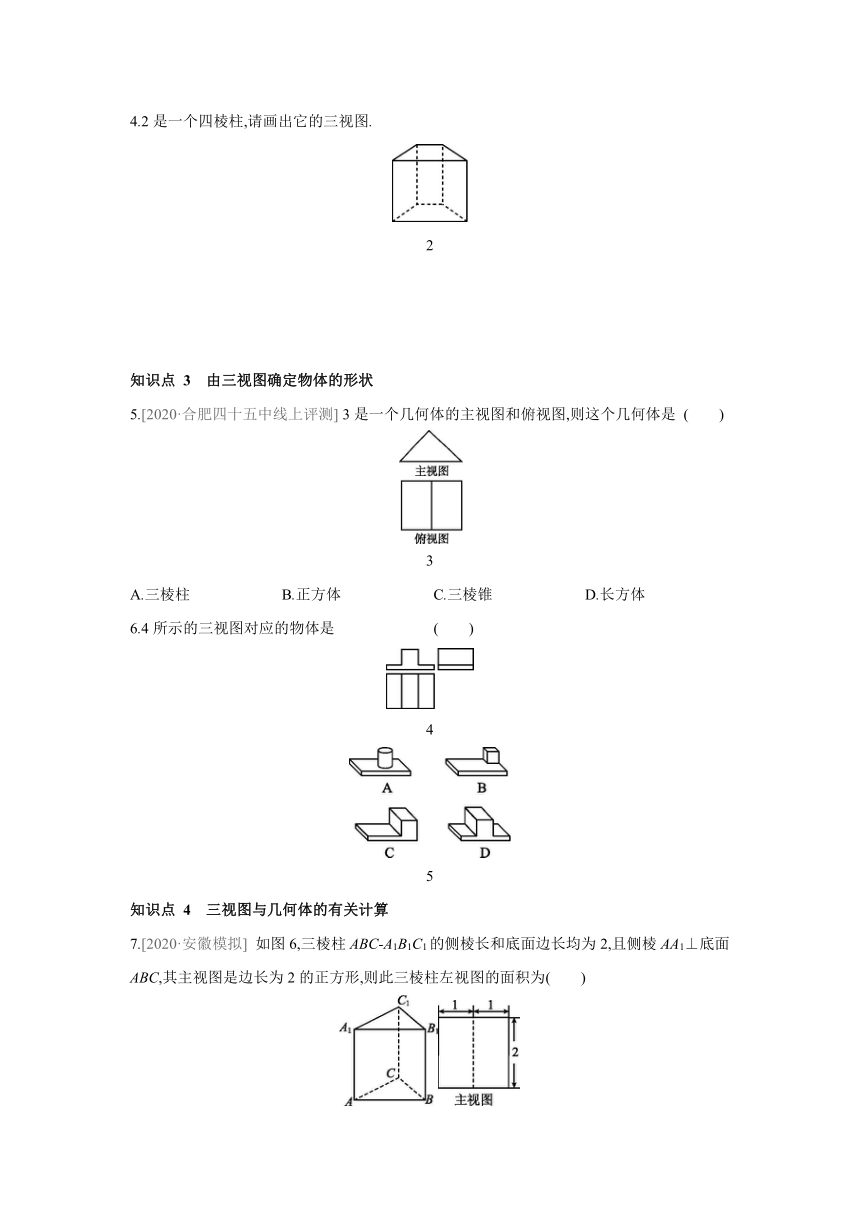
4.2是一个四棱柱,请画出它的三视图.
2
知识点 3 由三视图确定物体的形状
5.[2020·合肥四十五中线上评测] 3是一个几何体的主视图和俯视图,则这个几何体是 ( )
3
A.三棱柱 B.正方体 C.三棱锥 D.长方体
6.4所示的三视图对应的物体是 ( )
4
5
知识点 4 三视图与几何体的有关计算
7.[2020·安徽模拟] 如图6,三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,且侧棱AA1⊥底面ABC,其主视图是边长为2的正方形,则此三棱柱左视图的面积为( )
6
A. B.2 C.2 D.4
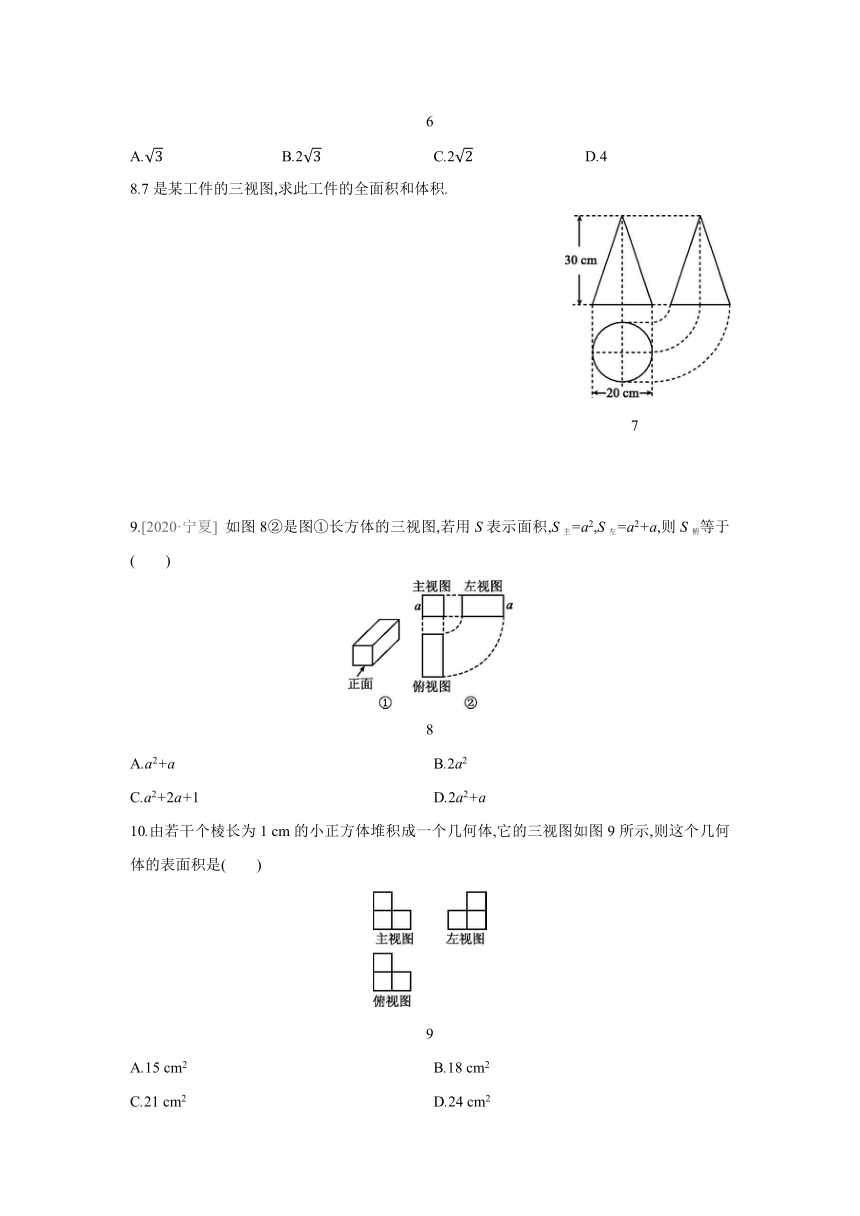
8.7是某工件的三视图,求此工件的全面积和体积.
7
9.[2020·宁夏] 如图8②是图①长方体的三视图,若用S表示面积,S主=a2,S左=a2+a,则S俯等于 ( )
8
A.a2+a B.2a2
C.a2+2a+1 D.2a2+a
10.由若干个棱长为1 cm的小正方体堆积成一个几何体,它的三视图如图9所示,则这个几何体的表面积是( )
9
A.15 cm2 B.18 cm2
C.21 cm2 D.24 cm2
11.某几何体的三视图如图0所示,则下列说法错误的是 ( )
0
A.该几何体是长方体
B.该几何体的高是3
C.底面有一边的长是1
D.该几何体的表面积为18
12.[2020·荆门改编] 如图1是一个几何体的三视图,求该几何体的全面积和体积.
1
13.一个几何体的三视图如图2所示,它的俯视图为菱形.
(1)请写出该几何体的形状;
(2)根据图中所给的数据求出它的侧面积.
2
14.3是由一些棱长为1的小立方块所搭几何体的三种视图.若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个大长方体,则至少还需要多少个小立方块 最终搭成的大长方体的表面积是多少
3
答案
1.D
2.B 选项A是它的主视图,选项B不是它的三视图,选项C是它的左视图,选项D是它的俯视图.
3.C
4.解:如图图所示:
5.A
6.D 根据俯视图可以看出直观图的下面部分为三个长方体,且三个长方体的宽度相同.只有选项D满足这两点.
7.B 由题意知三棱柱的底面为等边三角形,边长为2,作出等边三角形的高后,组成直角三角形,底边的一半为1,
∴等边三角形的高为,即左视图左右方向上的长度为,
∴左视图的面积为2×=2.
故选B.
8.解:由三视图可知,该工件为底面半径为10 cm,高为30 cm的圆锥体,则圆锥的母线长为=10(cm).
圆锥的侧面积S侧=lR=×20π×10=100π(cm2),
圆锥的底面积S底=102π=100π(cm2),
∴圆锥的全面积为100π+100π=100(1+)π cm2;
圆锥的体积为×100π×30=1000π(cm3).
故此工件的全面积是100(1+)π cm2,体积是1000π cm3.
9.A ∵S主=a2,S左=a2+a=a(a+1),
∴俯视图的长为a+1,宽为a,
∴S俯=a·(a+1)=a2+a.
故选A.
10.B
11.D 由三视图可知该几何体是长方体,高为3,底面有一边的长是1,表面积为2(1×2+2×3+1×3)=22.
故选D.
12.解:由三视图可知,该几何体是三棱柱,它的底面是底边长为2,底边上的高为1的等腰三角形,棱柱的高为2,则
S全=2S底+S侧
=2××2×1+2×(2+×2)
=2+4+4
=6+4.
V=×2×1×2=2.
答:该几何体的全面积是6+4,体积是2.
13.解:(1)该几何体的形状是直四棱柱.
(2)由三视图,知棱柱底面菱形的对角线长分别为4 cm,3 cm,∴菱形的边长为 cm,
∴棱柱的侧面积为×8×4=80(cm2).
14.解:由俯视图易得最底层有7个小立方块,第二层有2个小立方块,第三层有1个小立方块,其小立方块分布情况如图下:
则原几何体共由7+2+1=10(个)小立方块组成.
若搭成一个大长方体,则共需3×4×3=36(个)小立方块,所以还需36-10=26(个)小立方块,
最终搭成的大长方体的表面积是3×4×2+3×3×2+3×4×2=66.
知识点 1 棱柱的三视图
1.[2020·眉山] 如图6所示的几何体的主视图为 ( )
6
7
2.8所示的几何体是一个正三棱柱,9中不是其三视图的是 ( )
8
9
3.0所示的正六棱柱的左视图是 ( )
0
1
知识点 2 棱柱的三视图的画法
4.2是一个四棱柱,请画出它的三视图.
2
知识点 3 由三视图确定物体的形状
5.[2020·合肥四十五中线上评测] 3是一个几何体的主视图和俯视图,则这个几何体是 ( )
3
A.三棱柱 B.正方体 C.三棱锥 D.长方体
6.4所示的三视图对应的物体是 ( )
4
5
知识点 4 三视图与几何体的有关计算
7.[2020·安徽模拟] 如图6,三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,且侧棱AA1⊥底面ABC,其主视图是边长为2的正方形,则此三棱柱左视图的面积为( )
6
A. B.2 C.2 D.4
8.7是某工件的三视图,求此工件的全面积和体积.
7
9.[2020·宁夏] 如图8②是图①长方体的三视图,若用S表示面积,S主=a2,S左=a2+a,则S俯等于 ( )
8
A.a2+a B.2a2
C.a2+2a+1 D.2a2+a
10.由若干个棱长为1 cm的小正方体堆积成一个几何体,它的三视图如图9所示,则这个几何体的表面积是( )
9
A.15 cm2 B.18 cm2
C.21 cm2 D.24 cm2
11.某几何体的三视图如图0所示,则下列说法错误的是 ( )
0
A.该几何体是长方体
B.该几何体的高是3
C.底面有一边的长是1
D.该几何体的表面积为18
12.[2020·荆门改编] 如图1是一个几何体的三视图,求该几何体的全面积和体积.
1
13.一个几何体的三视图如图2所示,它的俯视图为菱形.
(1)请写出该几何体的形状;
(2)根据图中所给的数据求出它的侧面积.
2
14.3是由一些棱长为1的小立方块所搭几何体的三种视图.若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个大长方体,则至少还需要多少个小立方块 最终搭成的大长方体的表面积是多少
3
答案
1.D
2.B 选项A是它的主视图,选项B不是它的三视图,选项C是它的左视图,选项D是它的俯视图.
3.C
4.解:如图图所示:
5.A
6.D 根据俯视图可以看出直观图的下面部分为三个长方体,且三个长方体的宽度相同.只有选项D满足这两点.
7.B 由题意知三棱柱的底面为等边三角形,边长为2,作出等边三角形的高后,组成直角三角形,底边的一半为1,
∴等边三角形的高为,即左视图左右方向上的长度为,
∴左视图的面积为2×=2.
故选B.
8.解:由三视图可知,该工件为底面半径为10 cm,高为30 cm的圆锥体,则圆锥的母线长为=10(cm).
圆锥的侧面积S侧=lR=×20π×10=100π(cm2),
圆锥的底面积S底=102π=100π(cm2),
∴圆锥的全面积为100π+100π=100(1+)π cm2;
圆锥的体积为×100π×30=1000π(cm3).
故此工件的全面积是100(1+)π cm2,体积是1000π cm3.
9.A ∵S主=a2,S左=a2+a=a(a+1),
∴俯视图的长为a+1,宽为a,
∴S俯=a·(a+1)=a2+a.
故选A.
10.B
11.D 由三视图可知该几何体是长方体,高为3,底面有一边的长是1,表面积为2(1×2+2×3+1×3)=22.
故选D.
12.解:由三视图可知,该几何体是三棱柱,它的底面是底边长为2,底边上的高为1的等腰三角形,棱柱的高为2,则
S全=2S底+S侧
=2××2×1+2×(2+×2)
=2+4+4
=6+4.
V=×2×1×2=2.
答:该几何体的全面积是6+4,体积是2.
13.解:(1)该几何体的形状是直四棱柱.
(2)由三视图,知棱柱底面菱形的对角线长分别为4 cm,3 cm,∴菱形的边长为 cm,
∴棱柱的侧面积为×8×4=80(cm2).
14.解:由俯视图易得最底层有7个小立方块,第二层有2个小立方块,第三层有1个小立方块,其小立方块分布情况如图下:
则原几何体共由7+2+1=10(个)小立方块组成.
若搭成一个大长方体,则共需3×4×3=36(个)小立方块,所以还需36-10=26(个)小立方块,
最终搭成的大长方体的表面积是3×4×2+3×3×2+3×4×2=66.
