沪科版数学九年级下册同步课时练习:24.7 第1课时 弧长与扇形面积(word版含答案)
文档属性
| 名称 | 沪科版数学九年级下册同步课时练习:24.7 第1课时 弧长与扇形面积(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 165.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 00:00:00 | ||
图片预览


文档简介
24.7 第1课时 弧长与扇形面积
知识点 1 弧长公式及其应用
1.在半径为R的圆中,1°的圆心角所对的弧长l= ,n°的圆心角所对的弧长l= .
2.若扇形的圆心角为90°,半径为6,则该扇形的弧长为 ( )
A.π B.2π C.3π D.6π
3.如图,点A,B,C在半径为6的☉O上,的长为2π,则∠ACB的度数是 ( )
A.20° B.30° C.45° D.60°
4.如图,PA,PB是☉O的切线,切点分别是A,B,如图果∠P=60°,OA=3,那么∠AOB所对劣弧的长度为 ( )
A.6π B.5π C.3π D.2π
5.(1)一个扇形的弧长是11π cm,半径是18 cm,则此扇形的圆心角是 °.
(2)已知9°的圆周角所对的弧长是 cm,则此弧所在圆的半径是 .
6.如图,点A,B,C在☉O上,AB为☉O的直径,且AB=4,AC=2.
(1)求∠ABC的度数;
(2)求的长度.
知识点 2 扇形面积及其计算
7.已知一个扇形的半径为6,圆心角为120°,则该扇形的面积是 ( )
A.2π B.4π C.12π D.24π
8.一个扇形的圆心角是120°,面积为3π cm2,则这个扇形的半径是 ( )
A.1 cm B.3 cm C.6 cm D.9 cm
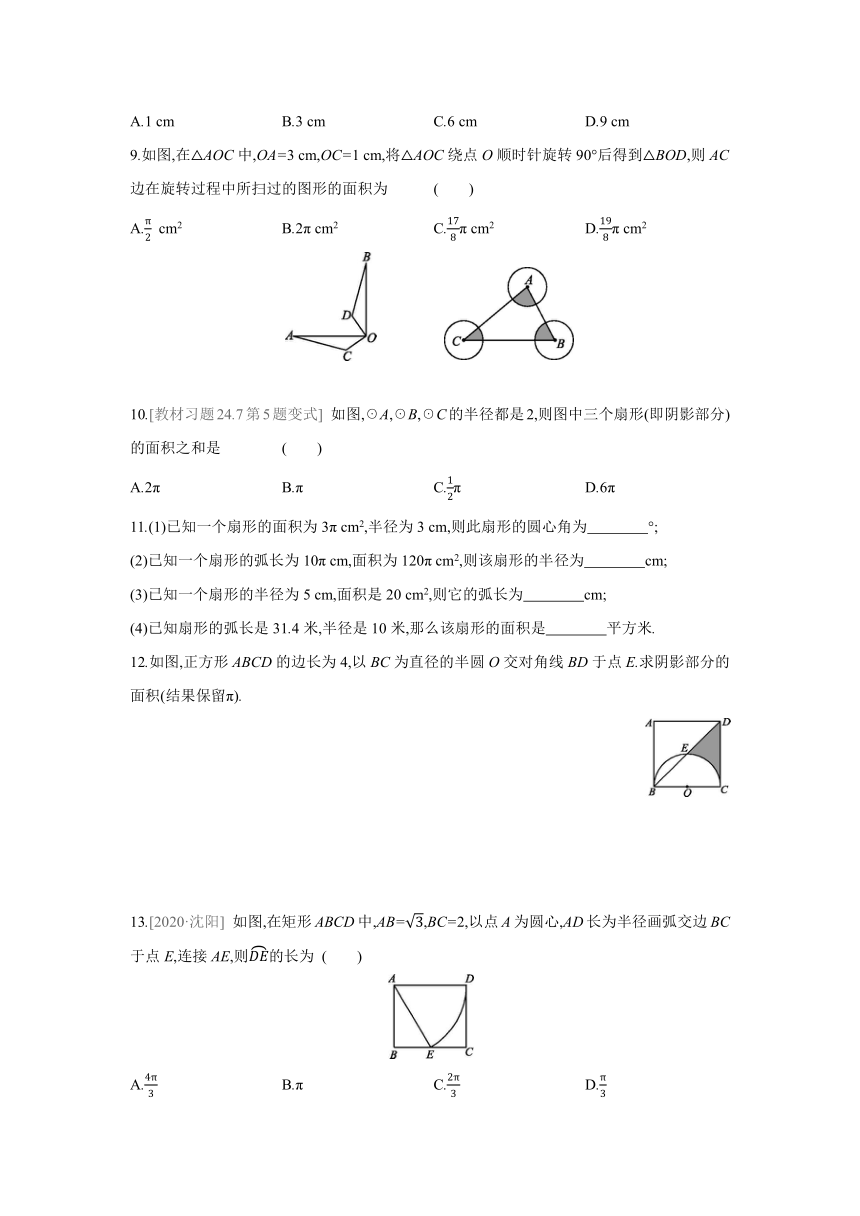
9.如图,在△AOC中,OA=3 cm,OC=1 cm,将△AOC绕点O顺时针旋转90°后得到△BOD,则AC边在旋转过程中所扫过的图形的面积为 ( )
A. cm2 B.2π cm2 C.π cm2 D.π cm2
10.[教材习题24.7第5题变式] 如图,☉A,☉B,☉C的半径都是2,则图中三个扇形(即阴影部分)的面积之和是 ( )
A.2π B.π C.π D.6π
11.(1)已知一个扇形的面积为3π cm2,半径为3 cm,则此扇形的圆心角为 °;
(2)已知一个扇形的弧长为10π cm,面积为120π cm2,则该扇形的半径为 cm;
(3)已知一个扇形的半径为5 cm,面积是20 cm2,则它的弧长为 cm;
(4)已知扇形的弧长是31.4米,半径是10米,那么该扇形的面积是 平方米.
12.如图,正方形ABCD的边长为4,以BC为直径的半圆O交对角线BD于点E.求阴影部分的面积(结果保留π).
13.[2020·沈阳] 如图,在矩形ABCD中,AB=,BC=2,以点A为圆心,AD长为半径画弧交边BC于点E,连接AE,则的长为 ( )
A. B.π C. D.
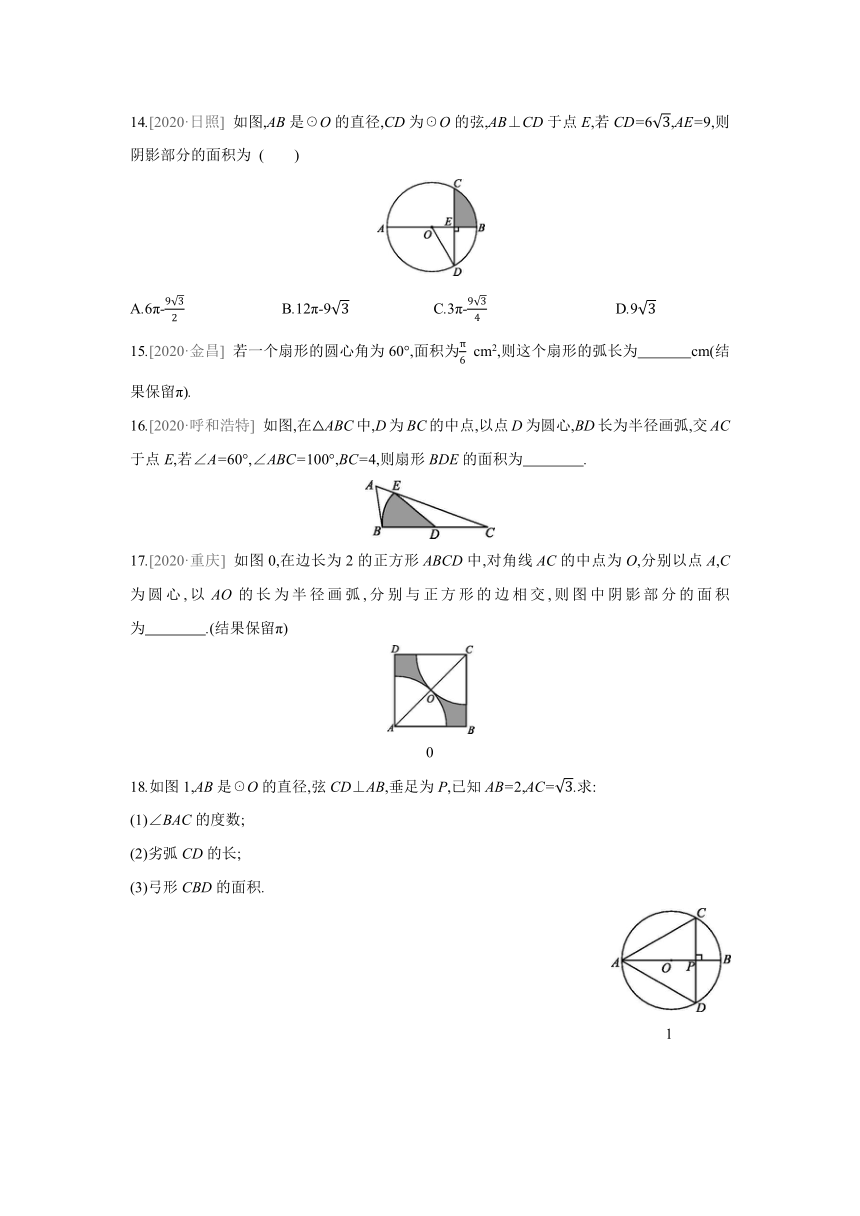
14.[2020·日照] 如图,AB是☉O的直径,CD为☉O的弦,AB⊥CD于点E,若CD=6,AE=9,则阴影部分的面积为 ( )
A.6π- B.12π-9 C.3π- D.9
15.[2020·金昌] 若一个扇形的圆心角为60°,面积为 cm2,则这个扇形的弧长为 cm(结果保留π).
16.[2020·呼和浩特] 如图,在△ABC中,D为BC的中点,以点D为圆心,BD长为半径画弧,交AC于点E,若∠A=60°,∠ABC=100°,BC=4,则扇形BDE的面积为 .
17.[2020·重庆] 如图0,在边长为2的正方形ABCD中,对角线AC的中点为O,分别以点A,C为圆心,以AO的长为半径画弧,分别与正方形的边相交,则图中阴影部分的面积为 .(结果保留π)
0
18.如图1,AB是☉O的直径,弦CD⊥AB,垂足为P,已知AB=2,AC=.求:
(1)∠BAC的度数;
(2)劣弧CD的长;
(3)弓形CBD的面积.
1
19.如图2,在扇形AOB中,∠AOB=90°,C为OA的中点,CE⊥OA交于点E.以点O为圆心,OC的长为半径作交OB于点D.若OA=2,求阴影部分的面积.
2
答案
1. 2.C 3.B
4.D ∵PA,PB是☉O的切线,∴∠OAP=∠OBP=90°.∵∠P=60°,∴∠AOB=180°-∠P=120°,∴∠AOB所对劣弧的长度==2π.故选D.
5.(1)110 (2)2 cm
6.解:(1)∵AB为☉O的直径,∴∠C=90°.
∵AB=4,AC=2,∴sinB==,
∴∠ABC=30°.
(2)连接OC.∵∠B=30°,∴∠AOC=60°,
∴的长度==π.
7.C
8.B 设扇形的半径为R.
由题意,得3π=,解得R=±3.
∵R>0,∴R=3 cm,∴这个扇形的半径为3 cm.故选B.
9.B
10.A ∵∠A+∠B+∠C=180°,
∴阴影部分的面积=π×22=2π.
11.(1)120 (2)24 (3)8 (4)157
12.解:如图图,连接OE.
∵四边形ABCD是正方形,
∴∠CBD=45°.
∵正方形ABCD的边长为4,
∴OB=OE=2,∴∠BOE=90°,
∴S阴影=S梯形CDEO-S扇形COE=×(2+4)×2-π×22=6-π.
13.C ∵四边形ABCD是矩形,
∴AD=BC=2,∠B=90°,
∴AE=AD=2.
∵AB=,
∴cos∠BAE==,
∴∠BAE=30°,
∴∠EAD=60°,
∴的长==.
故选C.
14.A
15. 设扇形的半径为R cm,弧长为l cm.
根据扇形的面积公式,得=,
解得R=1(负值已舍去).
∵扇形的面积=lR=,
∴l=.
故答案为.
16. ∵∠A=60°,∠ABC=100°,
∴∠C=20°.
又∵D为BC的中点,
∴BD=DC=BC=2.
∵DE=DB,
∴DE=DC=2,
∴∠DEC=∠C=20°,
∴∠BDE=40°,
∴扇形BDE的面积==.
故答案为.
17.4-π ∵四边形ABCD为正方形,
∴AB=BC=2,∠DAB=∠DCB=∠ABC=90°,
由勾股定理,得AC==2,
∴OA=OC=,
∴图中阴影部分的面积=22-×2=4-π.
故答案为4-π.
18.解:(1)如图图,连接BC.
∵AB是☉O的直径,
∴∠ACB=90°.
∵AB=2,AC=,
∴cos∠BAC==,
∴∠BAC=30°.
(2)如图图,连接OC,OD,∴∠BOC=2∠BAC=60°.
∵CD⊥AB,AB是☉O的直径,∴∠COD=120°,
∴劣弧CD的长是=.
(3)∵OC=OA=1,∠BOC=60°,
∴CP=OC·sin60°=1×=,
OP=OC·cos60°=,
∴CD=2CP=,
∴S弓形CBD=S扇形COD-S△OCD=-=-.
19.解:如图图,连接OE.
∵C是OA的中点,OA=2,
∴OC=OA=1.
∵OE=OA=2,
∴OC=OE.
又∵CE⊥OA,∴∠OEC=30°,∴∠COE=60°.
在Rt△OCE中,CE=OC·tan60°=,
∴S△OCE=OC·CE=.
∵∠AOB=90°,
∴∠BOE=∠AOB-∠COE=30°,
∴S扇形BOE==,S扇形COD==,
∴S阴影=S扇形BOE+S△OCE-S扇形COD=+-=+.
知识点 1 弧长公式及其应用
1.在半径为R的圆中,1°的圆心角所对的弧长l= ,n°的圆心角所对的弧长l= .
2.若扇形的圆心角为90°,半径为6,则该扇形的弧长为 ( )
A.π B.2π C.3π D.6π
3.如图,点A,B,C在半径为6的☉O上,的长为2π,则∠ACB的度数是 ( )
A.20° B.30° C.45° D.60°
4.如图,PA,PB是☉O的切线,切点分别是A,B,如图果∠P=60°,OA=3,那么∠AOB所对劣弧的长度为 ( )
A.6π B.5π C.3π D.2π
5.(1)一个扇形的弧长是11π cm,半径是18 cm,则此扇形的圆心角是 °.
(2)已知9°的圆周角所对的弧长是 cm,则此弧所在圆的半径是 .
6.如图,点A,B,C在☉O上,AB为☉O的直径,且AB=4,AC=2.
(1)求∠ABC的度数;
(2)求的长度.
知识点 2 扇形面积及其计算
7.已知一个扇形的半径为6,圆心角为120°,则该扇形的面积是 ( )
A.2π B.4π C.12π D.24π
8.一个扇形的圆心角是120°,面积为3π cm2,则这个扇形的半径是 ( )
A.1 cm B.3 cm C.6 cm D.9 cm
9.如图,在△AOC中,OA=3 cm,OC=1 cm,将△AOC绕点O顺时针旋转90°后得到△BOD,则AC边在旋转过程中所扫过的图形的面积为 ( )
A. cm2 B.2π cm2 C.π cm2 D.π cm2
10.[教材习题24.7第5题变式] 如图,☉A,☉B,☉C的半径都是2,则图中三个扇形(即阴影部分)的面积之和是 ( )
A.2π B.π C.π D.6π
11.(1)已知一个扇形的面积为3π cm2,半径为3 cm,则此扇形的圆心角为 °;
(2)已知一个扇形的弧长为10π cm,面积为120π cm2,则该扇形的半径为 cm;
(3)已知一个扇形的半径为5 cm,面积是20 cm2,则它的弧长为 cm;
(4)已知扇形的弧长是31.4米,半径是10米,那么该扇形的面积是 平方米.
12.如图,正方形ABCD的边长为4,以BC为直径的半圆O交对角线BD于点E.求阴影部分的面积(结果保留π).
13.[2020·沈阳] 如图,在矩形ABCD中,AB=,BC=2,以点A为圆心,AD长为半径画弧交边BC于点E,连接AE,则的长为 ( )
A. B.π C. D.
14.[2020·日照] 如图,AB是☉O的直径,CD为☉O的弦,AB⊥CD于点E,若CD=6,AE=9,则阴影部分的面积为 ( )
A.6π- B.12π-9 C.3π- D.9
15.[2020·金昌] 若一个扇形的圆心角为60°,面积为 cm2,则这个扇形的弧长为 cm(结果保留π).
16.[2020·呼和浩特] 如图,在△ABC中,D为BC的中点,以点D为圆心,BD长为半径画弧,交AC于点E,若∠A=60°,∠ABC=100°,BC=4,则扇形BDE的面积为 .
17.[2020·重庆] 如图0,在边长为2的正方形ABCD中,对角线AC的中点为O,分别以点A,C为圆心,以AO的长为半径画弧,分别与正方形的边相交,则图中阴影部分的面积为 .(结果保留π)
0
18.如图1,AB是☉O的直径,弦CD⊥AB,垂足为P,已知AB=2,AC=.求:
(1)∠BAC的度数;
(2)劣弧CD的长;
(3)弓形CBD的面积.
1
19.如图2,在扇形AOB中,∠AOB=90°,C为OA的中点,CE⊥OA交于点E.以点O为圆心,OC的长为半径作交OB于点D.若OA=2,求阴影部分的面积.
2
答案
1. 2.C 3.B
4.D ∵PA,PB是☉O的切线,∴∠OAP=∠OBP=90°.∵∠P=60°,∴∠AOB=180°-∠P=120°,∴∠AOB所对劣弧的长度==2π.故选D.
5.(1)110 (2)2 cm
6.解:(1)∵AB为☉O的直径,∴∠C=90°.
∵AB=4,AC=2,∴sinB==,
∴∠ABC=30°.
(2)连接OC.∵∠B=30°,∴∠AOC=60°,
∴的长度==π.
7.C
8.B 设扇形的半径为R.
由题意,得3π=,解得R=±3.
∵R>0,∴R=3 cm,∴这个扇形的半径为3 cm.故选B.
9.B
10.A ∵∠A+∠B+∠C=180°,
∴阴影部分的面积=π×22=2π.
11.(1)120 (2)24 (3)8 (4)157
12.解:如图图,连接OE.
∵四边形ABCD是正方形,
∴∠CBD=45°.
∵正方形ABCD的边长为4,
∴OB=OE=2,∴∠BOE=90°,
∴S阴影=S梯形CDEO-S扇形COE=×(2+4)×2-π×22=6-π.
13.C ∵四边形ABCD是矩形,
∴AD=BC=2,∠B=90°,
∴AE=AD=2.
∵AB=,
∴cos∠BAE==,
∴∠BAE=30°,
∴∠EAD=60°,
∴的长==.
故选C.
14.A
15. 设扇形的半径为R cm,弧长为l cm.
根据扇形的面积公式,得=,
解得R=1(负值已舍去).
∵扇形的面积=lR=,
∴l=.
故答案为.
16. ∵∠A=60°,∠ABC=100°,
∴∠C=20°.
又∵D为BC的中点,
∴BD=DC=BC=2.
∵DE=DB,
∴DE=DC=2,
∴∠DEC=∠C=20°,
∴∠BDE=40°,
∴扇形BDE的面积==.
故答案为.
17.4-π ∵四边形ABCD为正方形,
∴AB=BC=2,∠DAB=∠DCB=∠ABC=90°,
由勾股定理,得AC==2,
∴OA=OC=,
∴图中阴影部分的面积=22-×2=4-π.
故答案为4-π.
18.解:(1)如图图,连接BC.
∵AB是☉O的直径,
∴∠ACB=90°.
∵AB=2,AC=,
∴cos∠BAC==,
∴∠BAC=30°.
(2)如图图,连接OC,OD,∴∠BOC=2∠BAC=60°.
∵CD⊥AB,AB是☉O的直径,∴∠COD=120°,
∴劣弧CD的长是=.
(3)∵OC=OA=1,∠BOC=60°,
∴CP=OC·sin60°=1×=,
OP=OC·cos60°=,
∴CD=2CP=,
∴S弓形CBD=S扇形COD-S△OCD=-=-.
19.解:如图图,连接OE.
∵C是OA的中点,OA=2,
∴OC=OA=1.
∵OE=OA=2,
∴OC=OE.
又∵CE⊥OA,∴∠OEC=30°,∴∠COE=60°.
在Rt△OCE中,CE=OC·tan60°=,
∴S△OCE=OC·CE=.
∵∠AOB=90°,
∴∠BOE=∠AOB-∠COE=30°,
∴S扇形BOE==,S扇形COD==,
∴S阴影=S扇形BOE+S△OCE-S扇形COD=+-=+.
