沪科版数学九年级下册同步课时练习:第25章 投影与视图 自我综合评价(word版含答案)
文档属性
| 名称 | 沪科版数学九年级下册同步课时练习:第25章 投影与视图 自我综合评价(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 188.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 00:00:00 | ||
图片预览

文档简介
自我综合评价
第25章 投影与视图
一、选择题(每小题5分,共40分)
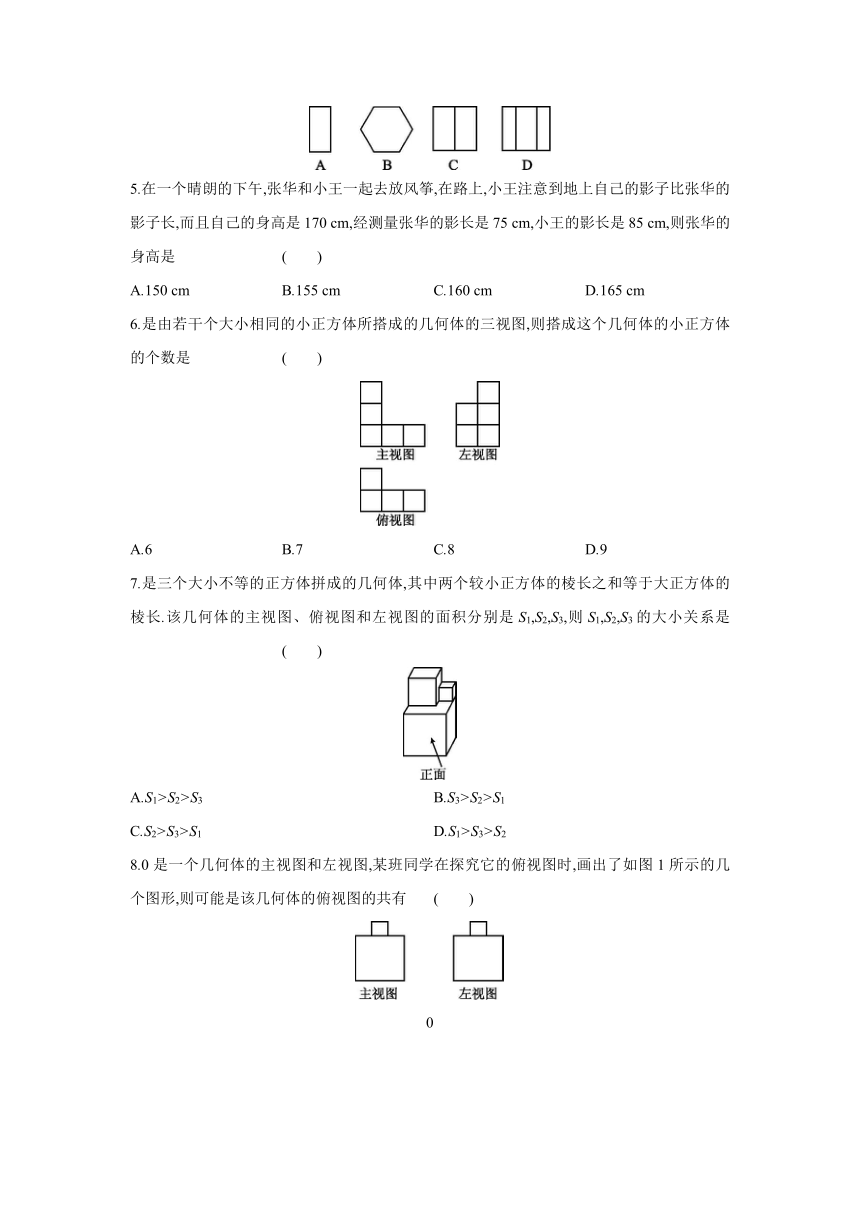
1.四个直立在地面上的字母广告牌在不同情况下,在地面上的投影(阴影部分)效果如图.则在字母L,K,C的投影中,与字母N属同一种投影的有 ( )
A.L,K B.C
C.K D.L,K,C
2.一个由圆柱和三棱柱组成的几何体如图水平放置,其主视图是 ( )
3.是一个机械零部件,该零部件的左视图是 ( )
4.如图,下列选项中不是正六棱柱的三视图的是 ( )
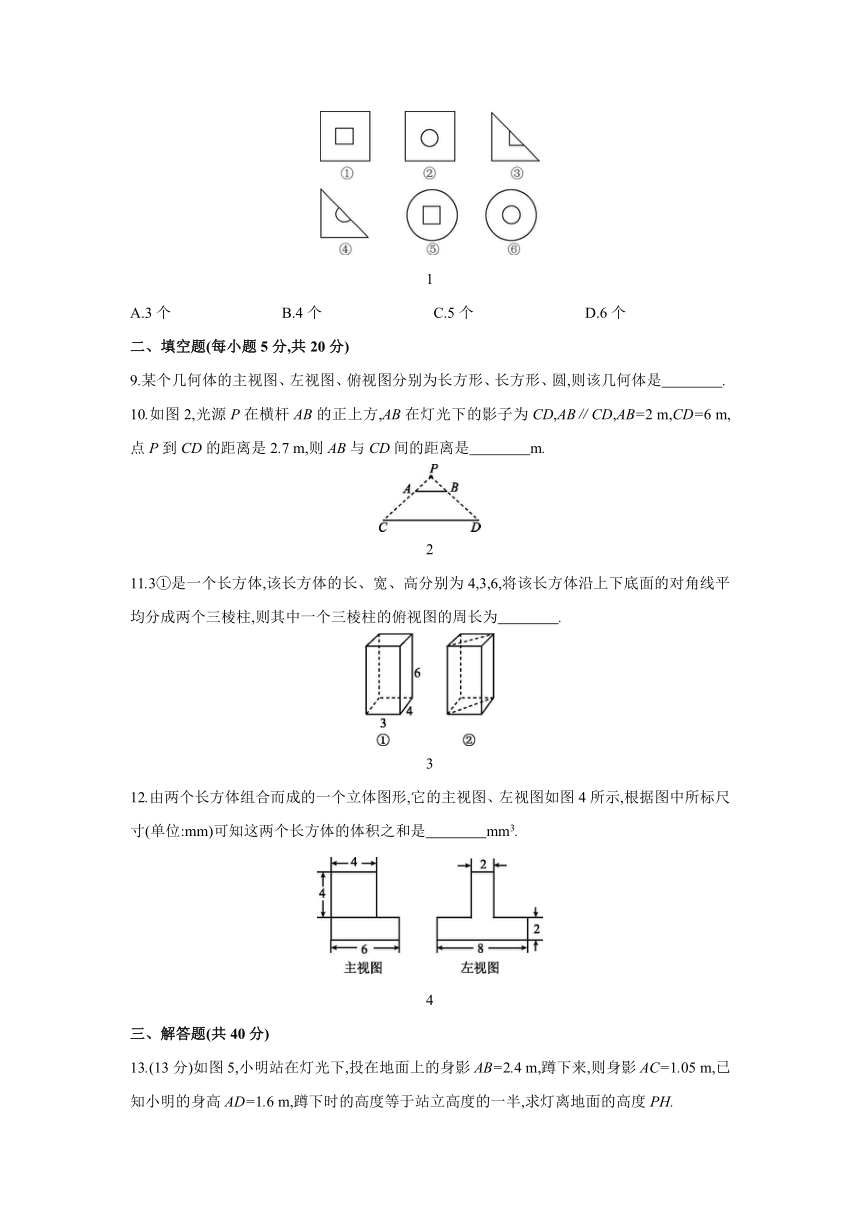
5.在一个晴朗的下午,张华和小王一起去放风筝,在路上,小王注意到地上自己的影子比张华的影子长,而且自己的身高是170 cm,经测量张华的影长是75 cm,小王的影长是85 cm,则张华的身高是 ( )
A.150 cm B.155 cm C.160 cm D.165 cm
6.是由若干个大小相同的小正方体所搭成的几何体的三视图,则搭成这个几何体的小正方体的个数是 ( )
A.6 B.7 C.8 D.9
7.是三个大小不等的正方体拼成的几何体,其中两个较小正方体的棱长之和等于大正方体的棱长.该几何体的主视图、俯视图和左视图的面积分别是S1,S2,S3,则S1,S2,S3的大小关系是 ( )
A.S1>S2>S3 B.S3>S2>S1
C.S2>S3>S1 D.S1>S3>S2
8.0是一个几何体的主视图和左视图,某班同学在探究它的俯视图时,画出了如图1所示的几个图形,则可能是该几何体的俯视图的共有 ( )
0
1
A.3个 B.4个 C.5个 D.6个
二、填空题(每小题5分,共20分)
9.某个几何体的主视图、左视图、俯视图分别为长方形、长方形、圆,则该几何体是 .
10.如图2,光源P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2 m,CD=6 m,点P到CD的距离是2.7 m,则AB与CD间的距离是 m.
2
11.3①是一个长方体,该长方体的长、宽、高分别为4,3,6,将该长方体沿上下底面的对角线平均分成两个三棱柱,则其中一个三棱柱的俯视图的周长为 .
3
12.由两个长方体组合而成的一个立体图形,它的主视图、左视图如图4所示,根据图中所标尺寸(单位:mm)可知这两个长方体的体积之和是 mm3.
4
三、解答题(共40分)
13.(13分)如图5,小明站在灯光下,投在地面上的身影AB=2.4 m,蹲下来,则身影AC=1.05 m,已知小明的身高AD=1.6 m,蹲下时的高度等于站立高度的一半,求灯离地面的高度PH.
5
14.(13分)一个圆柱形零件,削去了占底面圆四分之一部分的柱体(如图6①),现已画出了主视图与俯视图(如图图②).
(1)请只用直尺和圆规,将此零件的左视图画在规定的位置(不必写作法,只需保留作图痕迹);
(2)若此零件底面圆的半径r=2 cm,高h=3 cm,求此零件的表面积.
6
15.(14分)7是一个几何体的三视图.
(1)写出这个几何体的名称;
(2)根据图中所示数据计算这个几何体的表面积;
(3)如图果一只蚂蚁要从这个几何体的点B出发,沿表面爬到AC的中点D处,请你求出蚂蚁爬行的最短路程.
7
答案
【作者说卷】
考查意图 本试卷考查的重点是正投影的性质、三视图的画法、简单立体图形与其三视图之间的相互转化;难点是含有看不见棱的几何体的三视图的画法.试卷以选择题、填空题和解答题三种形式出现
知识与 技能 投影的概念与性质 1,5,10,13题
三视图的识别与画法 2,3,4,7,8,14题
由三视图描述几何体 6,9,12,15题
棱柱的概念与计算 11题
思想方法 方程思想
1.A 根据平行投影和中心投影的特点和规律,知“L”“K”与“N”属中心投影.故选A.
2.A 从正面看,上边是一个三角形,下边是一个矩形.故选A.
3.C
4.A 这个正六棱柱的主视图、左视图、俯视图分别为三个左右相邻的矩形、两个左右相邻的矩形、正六边形.故选A.
5.A
6.B 综合三视图可知,这个几何体的底层有4个小正方体,第二层有2个小正方体,第三层有1个小正方体,因此搭成这个几何体所用小正方体的个数是4+2+1=7.
7.D 主视图的面积是三个正方形的面积,左视图是两个正方形的面积,俯视图是一个正方形的面积,故S1>S3>S2.故选D.
8.C 9.圆柱
10.1.8 可以过点P作CD的高线,利用性质“对应高的比等于相似比”来解决问题.
11.12 分成的三棱柱的俯视图是直角三角形,两条直角边长分别为3和4,则斜边长为5,周长为3+4+5=12.
12.128 根据三视图可得:上面的长方体长4 mm,宽2 mm,高4 mm,下面的长方体长8 mm,宽6 mm,高2 mm,
∴立体图形的体积是4×4×2+6×8×2=128(mm3).
故答案为128.
13.解:设AD的中点为M.
∵AD∥PH,
∴△ADB∽△HPB,△AMC∽△HPC,
∴AB∶HB=AD∶PH,AC∶HC=AM∶PH,
即2.4∶(2.4+HA)=1.6∶PH,
1.05∶(1.05+HA)=0.8∶PH,解得PH=7.2.
即路灯的高度为7.2 m.
14.解:(1)左视图与主视图形状相同,有作垂线(直角)的痕迹(作法不唯一).
(2)零件的底面积为2πr2×=6π(cm2),
侧面积为2πr×+2r×3=(3π+4)×3=(9π+12)cm2,
6π+9π+12=(15π+12)cm2.
故零件的表面积为(15π+12)cm2.
15.解:(1)圆锥.
(2)S表=S侧+S底=×4 π×6+π×2=12π+4π=16π(cm2),即该几何体的表面积为16π cm2.
(3)如图图,将圆锥侧面展开,得到扇形ABB',则线段BD为所求的最短路程.
设∠BAB'=n°.
∵=4π,
∴n=120,即∠BAB'=120°.
连接CB.
∵C为弧BB'的中点,
∴∠BAC=60°,
∴△ABC为等边三角形.
又∵D为AC的中点,
∴∠ADB=90°,
∴BD=AB·sin∠BAD=6×=3(cm),
即蚂蚁爬行的最短路程为3 cm.
第25章 投影与视图
一、选择题(每小题5分,共40分)
1.四个直立在地面上的字母广告牌在不同情况下,在地面上的投影(阴影部分)效果如图.则在字母L,K,C的投影中,与字母N属同一种投影的有 ( )
A.L,K B.C
C.K D.L,K,C
2.一个由圆柱和三棱柱组成的几何体如图水平放置,其主视图是 ( )
3.是一个机械零部件,该零部件的左视图是 ( )
4.如图,下列选项中不是正六棱柱的三视图的是 ( )
5.在一个晴朗的下午,张华和小王一起去放风筝,在路上,小王注意到地上自己的影子比张华的影子长,而且自己的身高是170 cm,经测量张华的影长是75 cm,小王的影长是85 cm,则张华的身高是 ( )
A.150 cm B.155 cm C.160 cm D.165 cm
6.是由若干个大小相同的小正方体所搭成的几何体的三视图,则搭成这个几何体的小正方体的个数是 ( )
A.6 B.7 C.8 D.9
7.是三个大小不等的正方体拼成的几何体,其中两个较小正方体的棱长之和等于大正方体的棱长.该几何体的主视图、俯视图和左视图的面积分别是S1,S2,S3,则S1,S2,S3的大小关系是 ( )
A.S1>S2>S3 B.S3>S2>S1
C.S2>S3>S1 D.S1>S3>S2
8.0是一个几何体的主视图和左视图,某班同学在探究它的俯视图时,画出了如图1所示的几个图形,则可能是该几何体的俯视图的共有 ( )
0
1
A.3个 B.4个 C.5个 D.6个
二、填空题(每小题5分,共20分)
9.某个几何体的主视图、左视图、俯视图分别为长方形、长方形、圆,则该几何体是 .
10.如图2,光源P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2 m,CD=6 m,点P到CD的距离是2.7 m,则AB与CD间的距离是 m.
2
11.3①是一个长方体,该长方体的长、宽、高分别为4,3,6,将该长方体沿上下底面的对角线平均分成两个三棱柱,则其中一个三棱柱的俯视图的周长为 .
3
12.由两个长方体组合而成的一个立体图形,它的主视图、左视图如图4所示,根据图中所标尺寸(单位:mm)可知这两个长方体的体积之和是 mm3.
4
三、解答题(共40分)
13.(13分)如图5,小明站在灯光下,投在地面上的身影AB=2.4 m,蹲下来,则身影AC=1.05 m,已知小明的身高AD=1.6 m,蹲下时的高度等于站立高度的一半,求灯离地面的高度PH.
5
14.(13分)一个圆柱形零件,削去了占底面圆四分之一部分的柱体(如图6①),现已画出了主视图与俯视图(如图图②).
(1)请只用直尺和圆规,将此零件的左视图画在规定的位置(不必写作法,只需保留作图痕迹);
(2)若此零件底面圆的半径r=2 cm,高h=3 cm,求此零件的表面积.
6
15.(14分)7是一个几何体的三视图.
(1)写出这个几何体的名称;
(2)根据图中所示数据计算这个几何体的表面积;
(3)如图果一只蚂蚁要从这个几何体的点B出发,沿表面爬到AC的中点D处,请你求出蚂蚁爬行的最短路程.
7
答案
【作者说卷】
考查意图 本试卷考查的重点是正投影的性质、三视图的画法、简单立体图形与其三视图之间的相互转化;难点是含有看不见棱的几何体的三视图的画法.试卷以选择题、填空题和解答题三种形式出现
知识与 技能 投影的概念与性质 1,5,10,13题
三视图的识别与画法 2,3,4,7,8,14题
由三视图描述几何体 6,9,12,15题
棱柱的概念与计算 11题
思想方法 方程思想
1.A 根据平行投影和中心投影的特点和规律,知“L”“K”与“N”属中心投影.故选A.
2.A 从正面看,上边是一个三角形,下边是一个矩形.故选A.
3.C
4.A 这个正六棱柱的主视图、左视图、俯视图分别为三个左右相邻的矩形、两个左右相邻的矩形、正六边形.故选A.
5.A
6.B 综合三视图可知,这个几何体的底层有4个小正方体,第二层有2个小正方体,第三层有1个小正方体,因此搭成这个几何体所用小正方体的个数是4+2+1=7.
7.D 主视图的面积是三个正方形的面积,左视图是两个正方形的面积,俯视图是一个正方形的面积,故S1>S3>S2.故选D.
8.C 9.圆柱
10.1.8 可以过点P作CD的高线,利用性质“对应高的比等于相似比”来解决问题.
11.12 分成的三棱柱的俯视图是直角三角形,两条直角边长分别为3和4,则斜边长为5,周长为3+4+5=12.
12.128 根据三视图可得:上面的长方体长4 mm,宽2 mm,高4 mm,下面的长方体长8 mm,宽6 mm,高2 mm,
∴立体图形的体积是4×4×2+6×8×2=128(mm3).
故答案为128.
13.解:设AD的中点为M.
∵AD∥PH,
∴△ADB∽△HPB,△AMC∽△HPC,
∴AB∶HB=AD∶PH,AC∶HC=AM∶PH,
即2.4∶(2.4+HA)=1.6∶PH,
1.05∶(1.05+HA)=0.8∶PH,解得PH=7.2.
即路灯的高度为7.2 m.
14.解:(1)左视图与主视图形状相同,有作垂线(直角)的痕迹(作法不唯一).
(2)零件的底面积为2πr2×=6π(cm2),
侧面积为2πr×+2r×3=(3π+4)×3=(9π+12)cm2,
6π+9π+12=(15π+12)cm2.
故零件的表面积为(15π+12)cm2.
15.解:(1)圆锥.
(2)S表=S侧+S底=×4 π×6+π×2=12π+4π=16π(cm2),即该几何体的表面积为16π cm2.
(3)如图图,将圆锥侧面展开,得到扇形ABB',则线段BD为所求的最短路程.
设∠BAB'=n°.
∵=4π,
∴n=120,即∠BAB'=120°.
连接CB.
∵C为弧BB'的中点,
∴∠BAC=60°,
∴△ABC为等边三角形.
又∵D为AC的中点,
∴∠ADB=90°,
∴BD=AB·sin∠BAD=6×=3(cm),
即蚂蚁爬行的最短路程为3 cm.
