沪科版数学九年级下册同步课时练习:第26章 概率初步 复习小结(word版含答案)
文档属性
| 名称 | 沪科版数学九年级下册同步课时练习:第26章 概率初步 复习小结(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 154.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 00:00:00 | ||
图片预览


文档简介
第26章复习小结
类型之一 判断事件类型
1.[2021·怀化] “成语”是中华文化的瑰宝,是中华文化的微缩景观.下列成语:①“水中捞月”,②“守株待兔”,③“百步穿杨”,④“瓮中捉鳖”中描述的事件是不可能事件的是 ( )
A.① B.② C.③ D.④
2.[2020·泰州] 如,电路图上有4个开关S1,S2,S3,S4和1个小灯泡,同时闭合开关S1,S2或同时闭合开关S3,S4都可以使小灯泡发光.下列操作中,“小灯泡发光”这个事件是随机事件的是 ( )
A.只闭合1个开关 B.只闭合2个开关
C.只闭合3个开关 D.闭合4个开关
类型之二 用公式法求简单事件的概率
3.[2021·新疆] 不透明的袋子中有3个白球和2个红球,这些球除颜色外无其他差别,从袋子中随机摸出一个球,恰好是白球的概率为 ( )
A. B. C. D.
4.[2020·绍兴] 如图26-X-2,小球从A入口往下落,在每个交叉口都有向左或向右两种可能,且可能性相等,则小球从E出口落出的概率是 ( )
图26-X-2
A. B. C. D.
类型之三 用画树状图法或列表法求事件的概率
5.[2021·北京] 同时抛掷两枚质地均匀的硬币,则一枚硬币正面向上、一枚硬币反面向上的概率是 ( )
A. B. C. D.
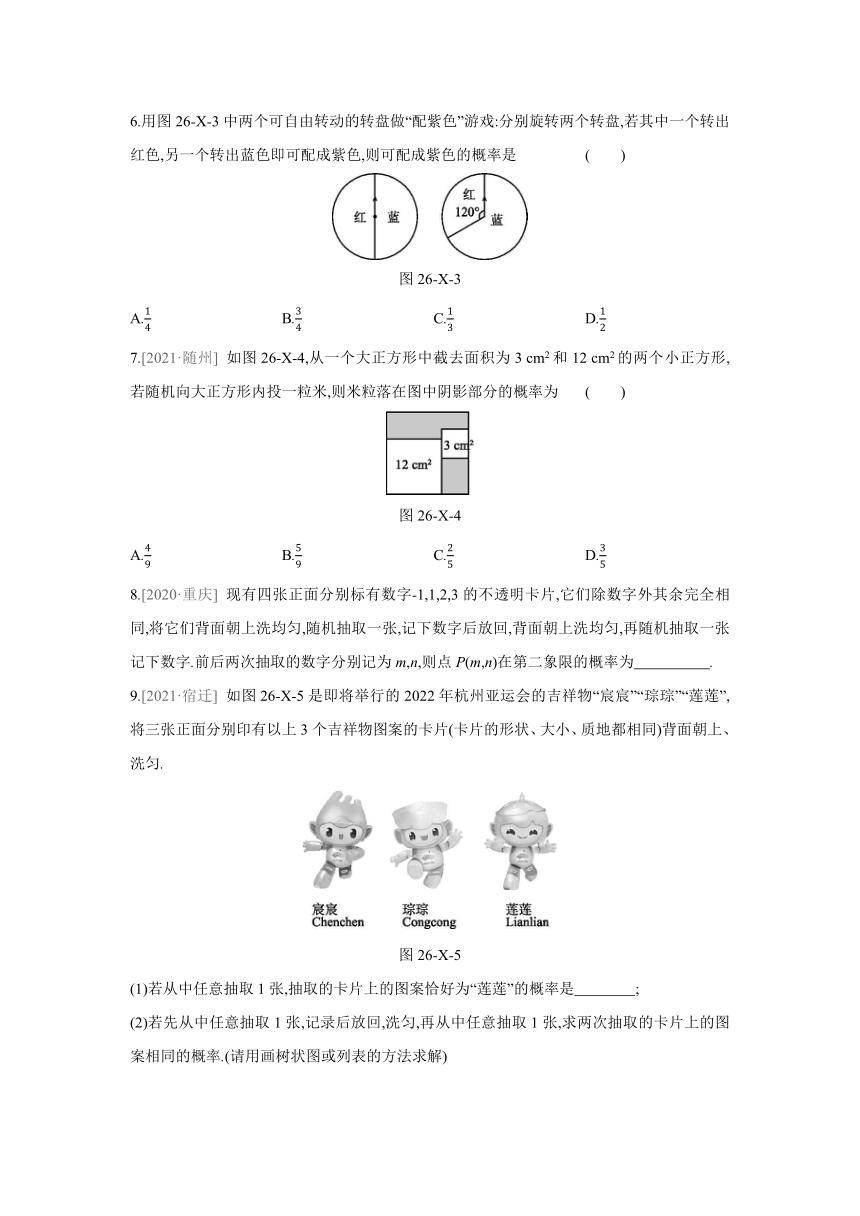
6.用图26-X-3中两个可自由转动的转盘做“配紫色”游戏:分别旋转两个转盘,若其中一个转出红色,另一个转出蓝色即可配成紫色,则可配成紫色的概率是 ( )
图26-X-3
A. B. C. D.
7.[2021·随州] 如图26-X-4,从一个大正方形中截去面积为3 cm2和12 cm2的两个小正方形,若随机向大正方形内投一粒米,则米粒落在图中阴影部分的概率为 ( )
图26-X-4
A. B. C. D.
8.[2020·重庆] 现有四张正面分别标有数字-1,1,2,3的不透明卡片,它们除数字外其余完全相同,将它们背面朝上洗均匀,随机抽取一张,记下数字后放回,背面朝上洗均匀,再随机抽取一张记下数字.前后两次抽取的数字分别记为m,n,则点P(m,n)在第二象限的概率为 .
9.[2021·宿迁] 如图26-X-5是即将举行的2022年杭州亚运会的吉祥物“宸宸”“琮琮”“莲莲”,将三张正面分别印有以上3个吉祥物图案的卡片(卡片的形状、大小、质地都相同)背面朝上、洗匀.
图26-X-5
(1)若从中任意抽取1张,抽取的卡片上的图案恰好为“莲莲”的概率是 ;
(2)若先从中任意抽取1张,记录后放回,洗匀,再从中任意抽取1张,求两次抽取的卡片上的图案相同的概率.(请用画树状图或列表的方法求解)
类型之四 用频率估计概率
10.[2020·芜湖期末] 在一个不透明的袋子里装有16个红球和若干个白球,这些球除颜色不同外无其他差别,每次从袋子里摸出一个球记录下颜色后再放回,经过大量的重复试验,发现摸到白球的频率稳定在0.6,则袋子里白球的个数大约是 .
11.一个不透明的袋子里装有8个黑球和若干个白球,这些球除颜色外其他完全相同.从袋中随机摸出1个球,记下其颜色,再把它放回袋中,不断重复上述的过程.
(1)若共摸球200次,其中有57次摸到黑球,你能估计摸出黑球的概率是多少吗 你能估计袋中大约有多少个白球吗
(2)若从袋中一次摸球20个,其中黑球数占,你能估计袋中大约有多少个白球吗
(3)打开口袋,数数袋中白球的个数,你的估计值和实际情况一致吗 为什么
(4)将各组的数据汇总,并根据这个数据估计袋中的白球数,看看估计结果又如何
(5)为了使估计结果较为准确,应该注意些什么
类型之五 用概率知识说明游戏是否公平
12.[2021·苏州] 4张相同的卡片上分别写有数字0,1,-2,3,将卡片背面朝上,洗匀后从中任意抽取1张,将卡片上的数字记录下来;再从余下的3张卡片中任意抽取1张,同样将卡片上的数字记录下来.
(1)第一次抽取的卡片上的数字是负数的概率为 .
(2)小敏设计了如下游戏规则:当第一次记录下来的数字减去第二次记录下来的数字所得结果为非负数时,甲获胜;否则,乙获胜.小敏设计的游戏规则公平吗 为什么 (请用画树状图或列表的方法说明理由)
类型之六 统计与概率的综合
13.为监控某条生产线上产品的质量,检测员每隔相同时间抽取一件产品,并测量其尺寸,在一天的抽检结束后,检测员将测得的数据按从小到大的顺序整理成如下表格:
编号 ① ② ③ ④ ⑤ ⑥ ⑦ ⑧
尺寸(cm) 8.72 8.88 8.92 8.93 8.94 8.96 8.97 8.98
编号 ⑨ ⑩
尺寸(cm) a 9.03 9.04 9.06 9.07 9.08 b
按照生产标准,产品等次规定如下:
尺寸(单位:cm) 产品等次
8.97≤x≤9.03 特等品
8.95≤x≤9.05 优等品
8.90≤x≤9.10 合格品
x<8.90或x>9.10 非合格品
注:在统计优等品个数时,将特等品计算在内;在统计合格品个数时,将优等品(含特等品)计算在内.
(1)已知此次抽检的合格率为80%,请判断编号为的产品是不是合格品,并说明理由.
(2)已知此次抽检出的优等品尺寸的中位数为9 cm.
(i)a= ;
(ii)将这些优等品分成两组,一组尺寸大于9 cm,另一组尺寸不大于9 cm,从这两组中各随机抽取1件进行复检,抽到的2件产品都是特等品的概率为 .
教师详解详析
1.A [解析] ①“水中捞月”是不可能事件,符合题意;
②“守株待兔”是随机事件,不符合题意;
③“百步穿杨”是随机事件,不符合题意;
④“瓮中捉鳖”是必然事件,不符合题意.
故选A.
2.B [解析] 只闭合1个开关,小灯泡不会发光,属于不可能事件,故A项不符合题意;只闭合2个开关,小灯泡可能发光也可能不发光,是随机事件,故B项符合题意;只闭合3个开关,小灯泡一定会发光,是必然事件,故C项不符合题意;闭合4个开关,小灯泡一定会发光,是必然事件,故D项不符合题意.故选B.
3.C [解析] ∵共有5个球,其中白球有3个,
∴随机摸出一个球,恰好是白球的概率是.
4.C [解析] 由题图可知,在每个交叉口都有向左或向右两种可能,且可能性相等,小球最终落出的出口共有E,F,G,H四个,所以小球从E出口落出的概率是.故选C.
5.C [解析] 画树状图如下:
由树状图可知共4种等可能的结果,一枚硬币正面向上、一枚硬币反面向上的结果有2种,
∴一枚硬币正面向上、一枚硬币反面向上的概率为=.故选C.
6.D
7.A [解析] 由图可知大正方形中的两个小正方形的边长分别为2 cm, cm,
∴大正方形的边长为2+=3(cm),
则大正方形的面积为(3)2=27(cm),
∴阴影部分的面积为27-12-3=12(cm2),
∴米粒落在图中阴影部分的概率为=.
故选A.
8. [解析] 画树状图如图.
共有16种等可能的结果,其中点P(m,n)在第二象限的结果有3种,所以点P(m,n)在第二象限的概率为.
9.解:(1)
(2)把吉祥物“宸宸”“琮琮”“莲莲”三张卡片分别记为A,B,C.
画树状图如图:
由图可知,共有9种等可能的结果,两次抽取的卡片上的图案相同的结果有3种,
∴两次抽取的卡片上的图案相同的概率为=.
10.24 [解析] 设袋子中白球的个数为x.
根据题意,得=0.6,
解得x=24.
经检验,x=24是分式方程的解.
所以袋子里白球的个数大约是24.
11.解:(1)估计摸出黑球的概率是.
球的总个数是8÷≈28,则估计袋中大约有白球28-8=20(个).
(2)袋子中球的总个数是8÷=32(个),
则估计袋中白球的个数是32-8=24(个).
(3)估计值和实际情况不一定一致.
理由:因为抽查具有随机性.
(4)摸球20个,其中黑球数占,则有5个黑球.
则球的总个数是8÷≈28,则白球的个数约是28-8=20(个).
(5)抽取的次数要尽量多,且抽取时是随机抽样.
12.解:(1)
(2)小敏设计的游戏规则公平.
理由:列表如下:
结果 第一次 第二次 0 1 -2 3
0 1 -2 3
1 -1 -3 2
-2 2 3 5
3 -3 -2 -5
由表可知,共有12种等可能结果,其中结果为非负数的有6种结果,结果为负数的有6种结果,所以甲获胜的概率=乙获胜的概率==,∴小敏设计的游戏规则公平.
13.[解析] (2)(i)优等品有⑥~,中位数在⑧8.98,⑨a之间,
∴=9,
解得a=9.02.
(ii)尺寸大于9 cm的有⑨⑩,尺寸不大于9 cm的有⑥⑦⑧,其中特等品为⑦⑧⑨⑩.
画树状图如下:
共有9种等可能的情况,其中抽到的2件产品都是特等品的情况有4种,
∴抽到的2件产品都是特等品的概率为.
解:(1)编号的产品不是合格品.理由如下:
∵15×80%=12(个),
∴不合格的有15-12=3(个).
∵编号①~中只有①②两个不合格,
∴编号的产品是不合格品.
(2)(ⅰ)9.02 (ⅱ)
类型之一 判断事件类型
1.[2021·怀化] “成语”是中华文化的瑰宝,是中华文化的微缩景观.下列成语:①“水中捞月”,②“守株待兔”,③“百步穿杨”,④“瓮中捉鳖”中描述的事件是不可能事件的是 ( )
A.① B.② C.③ D.④
2.[2020·泰州] 如,电路图上有4个开关S1,S2,S3,S4和1个小灯泡,同时闭合开关S1,S2或同时闭合开关S3,S4都可以使小灯泡发光.下列操作中,“小灯泡发光”这个事件是随机事件的是 ( )
A.只闭合1个开关 B.只闭合2个开关
C.只闭合3个开关 D.闭合4个开关
类型之二 用公式法求简单事件的概率
3.[2021·新疆] 不透明的袋子中有3个白球和2个红球,这些球除颜色外无其他差别,从袋子中随机摸出一个球,恰好是白球的概率为 ( )
A. B. C. D.
4.[2020·绍兴] 如图26-X-2,小球从A入口往下落,在每个交叉口都有向左或向右两种可能,且可能性相等,则小球从E出口落出的概率是 ( )
图26-X-2
A. B. C. D.
类型之三 用画树状图法或列表法求事件的概率
5.[2021·北京] 同时抛掷两枚质地均匀的硬币,则一枚硬币正面向上、一枚硬币反面向上的概率是 ( )
A. B. C. D.
6.用图26-X-3中两个可自由转动的转盘做“配紫色”游戏:分别旋转两个转盘,若其中一个转出红色,另一个转出蓝色即可配成紫色,则可配成紫色的概率是 ( )
图26-X-3
A. B. C. D.
7.[2021·随州] 如图26-X-4,从一个大正方形中截去面积为3 cm2和12 cm2的两个小正方形,若随机向大正方形内投一粒米,则米粒落在图中阴影部分的概率为 ( )
图26-X-4
A. B. C. D.
8.[2020·重庆] 现有四张正面分别标有数字-1,1,2,3的不透明卡片,它们除数字外其余完全相同,将它们背面朝上洗均匀,随机抽取一张,记下数字后放回,背面朝上洗均匀,再随机抽取一张记下数字.前后两次抽取的数字分别记为m,n,则点P(m,n)在第二象限的概率为 .
9.[2021·宿迁] 如图26-X-5是即将举行的2022年杭州亚运会的吉祥物“宸宸”“琮琮”“莲莲”,将三张正面分别印有以上3个吉祥物图案的卡片(卡片的形状、大小、质地都相同)背面朝上、洗匀.
图26-X-5
(1)若从中任意抽取1张,抽取的卡片上的图案恰好为“莲莲”的概率是 ;
(2)若先从中任意抽取1张,记录后放回,洗匀,再从中任意抽取1张,求两次抽取的卡片上的图案相同的概率.(请用画树状图或列表的方法求解)
类型之四 用频率估计概率
10.[2020·芜湖期末] 在一个不透明的袋子里装有16个红球和若干个白球,这些球除颜色不同外无其他差别,每次从袋子里摸出一个球记录下颜色后再放回,经过大量的重复试验,发现摸到白球的频率稳定在0.6,则袋子里白球的个数大约是 .
11.一个不透明的袋子里装有8个黑球和若干个白球,这些球除颜色外其他完全相同.从袋中随机摸出1个球,记下其颜色,再把它放回袋中,不断重复上述的过程.
(1)若共摸球200次,其中有57次摸到黑球,你能估计摸出黑球的概率是多少吗 你能估计袋中大约有多少个白球吗
(2)若从袋中一次摸球20个,其中黑球数占,你能估计袋中大约有多少个白球吗
(3)打开口袋,数数袋中白球的个数,你的估计值和实际情况一致吗 为什么
(4)将各组的数据汇总,并根据这个数据估计袋中的白球数,看看估计结果又如何
(5)为了使估计结果较为准确,应该注意些什么
类型之五 用概率知识说明游戏是否公平
12.[2021·苏州] 4张相同的卡片上分别写有数字0,1,-2,3,将卡片背面朝上,洗匀后从中任意抽取1张,将卡片上的数字记录下来;再从余下的3张卡片中任意抽取1张,同样将卡片上的数字记录下来.
(1)第一次抽取的卡片上的数字是负数的概率为 .
(2)小敏设计了如下游戏规则:当第一次记录下来的数字减去第二次记录下来的数字所得结果为非负数时,甲获胜;否则,乙获胜.小敏设计的游戏规则公平吗 为什么 (请用画树状图或列表的方法说明理由)
类型之六 统计与概率的综合
13.为监控某条生产线上产品的质量,检测员每隔相同时间抽取一件产品,并测量其尺寸,在一天的抽检结束后,检测员将测得的数据按从小到大的顺序整理成如下表格:
编号 ① ② ③ ④ ⑤ ⑥ ⑦ ⑧
尺寸(cm) 8.72 8.88 8.92 8.93 8.94 8.96 8.97 8.98
编号 ⑨ ⑩
尺寸(cm) a 9.03 9.04 9.06 9.07 9.08 b
按照生产标准,产品等次规定如下:
尺寸(单位:cm) 产品等次
8.97≤x≤9.03 特等品
8.95≤x≤9.05 优等品
8.90≤x≤9.10 合格品
x<8.90或x>9.10 非合格品
注:在统计优等品个数时,将特等品计算在内;在统计合格品个数时,将优等品(含特等品)计算在内.
(1)已知此次抽检的合格率为80%,请判断编号为的产品是不是合格品,并说明理由.
(2)已知此次抽检出的优等品尺寸的中位数为9 cm.
(i)a= ;
(ii)将这些优等品分成两组,一组尺寸大于9 cm,另一组尺寸不大于9 cm,从这两组中各随机抽取1件进行复检,抽到的2件产品都是特等品的概率为 .
教师详解详析
1.A [解析] ①“水中捞月”是不可能事件,符合题意;
②“守株待兔”是随机事件,不符合题意;
③“百步穿杨”是随机事件,不符合题意;
④“瓮中捉鳖”是必然事件,不符合题意.
故选A.
2.B [解析] 只闭合1个开关,小灯泡不会发光,属于不可能事件,故A项不符合题意;只闭合2个开关,小灯泡可能发光也可能不发光,是随机事件,故B项符合题意;只闭合3个开关,小灯泡一定会发光,是必然事件,故C项不符合题意;闭合4个开关,小灯泡一定会发光,是必然事件,故D项不符合题意.故选B.
3.C [解析] ∵共有5个球,其中白球有3个,
∴随机摸出一个球,恰好是白球的概率是.
4.C [解析] 由题图可知,在每个交叉口都有向左或向右两种可能,且可能性相等,小球最终落出的出口共有E,F,G,H四个,所以小球从E出口落出的概率是.故选C.
5.C [解析] 画树状图如下:
由树状图可知共4种等可能的结果,一枚硬币正面向上、一枚硬币反面向上的结果有2种,
∴一枚硬币正面向上、一枚硬币反面向上的概率为=.故选C.
6.D
7.A [解析] 由图可知大正方形中的两个小正方形的边长分别为2 cm, cm,
∴大正方形的边长为2+=3(cm),
则大正方形的面积为(3)2=27(cm),
∴阴影部分的面积为27-12-3=12(cm2),
∴米粒落在图中阴影部分的概率为=.
故选A.
8. [解析] 画树状图如图.
共有16种等可能的结果,其中点P(m,n)在第二象限的结果有3种,所以点P(m,n)在第二象限的概率为.
9.解:(1)
(2)把吉祥物“宸宸”“琮琮”“莲莲”三张卡片分别记为A,B,C.
画树状图如图:
由图可知,共有9种等可能的结果,两次抽取的卡片上的图案相同的结果有3种,
∴两次抽取的卡片上的图案相同的概率为=.
10.24 [解析] 设袋子中白球的个数为x.
根据题意,得=0.6,
解得x=24.
经检验,x=24是分式方程的解.
所以袋子里白球的个数大约是24.
11.解:(1)估计摸出黑球的概率是.
球的总个数是8÷≈28,则估计袋中大约有白球28-8=20(个).
(2)袋子中球的总个数是8÷=32(个),
则估计袋中白球的个数是32-8=24(个).
(3)估计值和实际情况不一定一致.
理由:因为抽查具有随机性.
(4)摸球20个,其中黑球数占,则有5个黑球.
则球的总个数是8÷≈28,则白球的个数约是28-8=20(个).
(5)抽取的次数要尽量多,且抽取时是随机抽样.
12.解:(1)
(2)小敏设计的游戏规则公平.
理由:列表如下:
结果 第一次 第二次 0 1 -2 3
0 1 -2 3
1 -1 -3 2
-2 2 3 5
3 -3 -2 -5
由表可知,共有12种等可能结果,其中结果为非负数的有6种结果,结果为负数的有6种结果,所以甲获胜的概率=乙获胜的概率==,∴小敏设计的游戏规则公平.
13.[解析] (2)(i)优等品有⑥~,中位数在⑧8.98,⑨a之间,
∴=9,
解得a=9.02.
(ii)尺寸大于9 cm的有⑨⑩,尺寸不大于9 cm的有⑥⑦⑧,其中特等品为⑦⑧⑨⑩.
画树状图如下:
共有9种等可能的情况,其中抽到的2件产品都是特等品的情况有4种,
∴抽到的2件产品都是特等品的概率为.
解:(1)编号的产品不是合格品.理由如下:
∵15×80%=12(个),
∴不合格的有15-12=3(个).
∵编号①~中只有①②两个不合格,
∴编号的产品是不合格品.
(2)(ⅰ)9.02 (ⅱ)
