沪科版数学九年级下册同步课时练习:24.2 第1课时 圆的有关概念及点与圆的位置关系(word版含答案)
文档属性
| 名称 | 沪科版数学九年级下册同步课时练习:24.2 第1课时 圆的有关概念及点与圆的位置关系(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 200.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 19:01:17 | ||
图片预览



文档简介
24.2 第1课时 圆的有关概念及点与圆的位置关系
知识点 1 圆的定义
1.如图,平面内有两点O和A,以下列语句画圆,画出的圆是唯一确定的是 ( )
A.以点O为圆心画圆
B.以OA的长为半径画圆
C.画圆使它经过点A
D.以点O为圆心,OA的长为半径画圆
2.在同一平面内,到点O的距离等于8的所有点组成的图形是 .
知识点 2 点与圆的位置关系
3.☉O的半径为5 cm,点A到圆心O的距离OA为3 cm,则点A与☉O的位置关系为 ( )
A.点A在圆上 B.点A在圆内
C.点A在圆外 D.无法确定
4.若☉O的直径为20 cm,有一点A(点A与圆心O不重合)在☉O内,则线段OA长的取值范围是( )
A.OA>20 cm B.OA>10 cm
C.0 cm5.[2020·安徽模拟] 如图果☉A的半径为5,圆心A的坐标是(1,2),点P的坐标是(5,2),那么点P的位置为 ( )
A.在☉A内 B.在☉A上
C.在☉A外 D.不能确定
6.如图所示,边长为1的正方形ABCD的对角线相交于点O,以点A为圆心,1为半径画圆,则点O,B,C,D中,点 在圆内,点 在圆上,点 在圆外.
7.已知☉O的半径为5 cm,A为线段OP的中点,当OP满足下列条件时,分别指出点A与☉O的位置关系.
(1)OP=8 cm;(2)OP=10 cm;(3)OP=12 cm.
知识点 3 与圆有关的概念
8.如图所示,AB是圆的直径,则图中的弦有 条,分别是 ,劣弧有
条,分别是 .以A为一个端点的优弧有 条,分别是 .
9.有下列说法:①直径是弦;②弦是直径;③半径相等的两个半圆是等弧;④长度相等的两条弧是等弧;⑤半圆是弧,但弧不一定是半圆.其中说法正确的有 ( )
A.1个 B.2个 C.3个 D.4个
10.已知:如图,在☉O中,AB为弦,C,D两点在弦AB上,且AC=BD.
求证:△OAC≌△OBD.
11.[教材例1变式] 如图,菱形ABCD的对角线AC,BD相交于点O,E,F,G,H分别是AB,BC,CD,DA的中点,点E,F,G,H在以点O为圆心的同一个圆上吗 为什么
12.在平面直角坐标系中,☉O的圆心为(1,0),半径为2,则下面各点在☉O上的是 ( )
A.(2,0) B.(0,2) C.(0,) D.(,0)
13.已知☉O的半径为1,点A到圆心O的距离为a.若关于x的方程x2-2x+a=0不存在实数根,则点A与☉O的位置关系是 ( )
A.点A在☉O上 B.点A在☉O外
C.点A在☉O内 D.无法确定
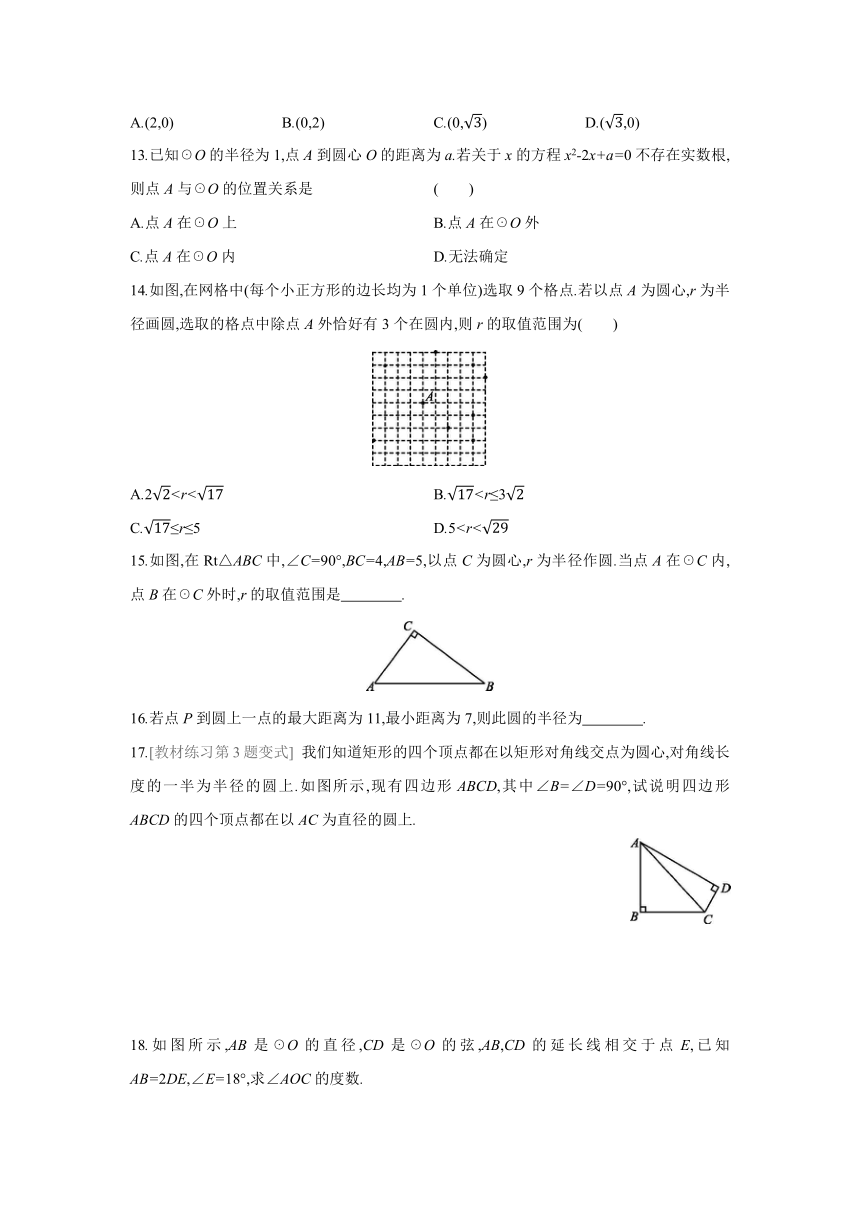
14.如图,在网格中(每个小正方形的边长均为1个单位)选取9个格点.若以点A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为( )
A.2C.≤r≤5 D.515.如图,在Rt△ABC中,∠C=90°,BC=4,AB=5,以点C为圆心,r为半径作圆.当点A在☉C内,点B在☉C外时,r的取值范围是 .
16.若点P到圆上一点的最大距离为11,最小距离为7,则此圆的半径为 .
17.[教材练习第3题变式] 我们知道矩形的四个顶点都在以矩形对角线交点为圆心,对角线长度的一半为半径的圆上.如图所示,现有四边形ABCD,其中∠B=∠D=90°,试说明四边形ABCD的四个顶点都在以AC为直径的圆上.
18.如图所示,AB是☉O的直径,CD是☉O的弦,AB,CD的延长线相交于点E,已知AB=2DE,∠E=18°,求∠AOC的度数.
19.如图0,已知过A,C,D三点的圆的圆心为点E,过B,E,F三点的圆的圆心为点D.如图果∠ABC=24°,那么∠CAE= °.
0
20.如图1,点A,D,G,M在半圆O上,四边形ABOC,DEOF,HMNO均为矩形.设BC=a,EF=b,HN=c,则a,b,c的大小关系是 .
1
答案
1.D
2.以点O为圆心,以8为半径的圆
3.B 点A到圆心的距离小于圆的半径,所以点A在圆的内部.故选B.
4.D 若点在圆内,则点到圆心的距离小于圆的半径.
5.A ∵圆心A的坐标是(1,2),点P的坐标是(5,2),
∴AP=4<5,∴点P在☉A内.
故选A.
6.O B,D C ∵四边形ABCD为正方形,∴AC⊥BD,OA=OB=OC=OD.
设OA=OB=x,
由勾股定理,得OA2+OB2=AB2,
即x2+x2=12,
解得x=(负值已舍去),
∴OA=<1,AC=>1.
即点O在圆内,点C在圆外.
∵AD=AB=1,∴点B,D在圆上.
7.解:(1)当OP=8 cm时,OA=OP=4 cm.
又☉O的半径为5 cm,所以点A在☉O内.
(2)当OP=10 cm时,OA=OP=5 cm.
又☉O的半径为5 cm,所以点A在☉O上.
(3)当OP=12 cm时,OA=OP=6 cm.
又☉O的半径为5 cm,所以点A在☉O外.
8.2 弦CD,弦AB 5 ,,,,
2 ,
本题考查对弦与劣弧、优弧的概念的理解.
9.C 正确的有①③⑤.
10.证明:∵OA=OB,
∴∠A=∠B.
在△OAC和△OBD中,
∵
∴△OAC≌△OBD(SAS).
11.解:点E,F,G,H在以点O为圆心的同一个圆上.理由:如图图,连接EO,HO,FO,GO.
∵四边形ABCD是菱形,
∴AC⊥BD,AB=BC=DC=AD,
∴∠AOB=∠AOD=∠BOC=∠COD=90°.
∵E,F,G,H分别是AB,BC,CD,DA的中点,
∴EO=FO=HO=GO=AB,
∴点E,F,G,H在以点O为圆心的同一个圆上.
12.C A项,点(2,0)到☉O的圆心(1,0)的距离为2-1=1<2,所以点(2,0)在☉O内,错误;
B项,点(0,2)到☉O的圆心(1,0)的距离为=>2,所以点(0,2)在☉O外,错误;
C项,点(0,)到☉O的圆心(1,0)的距离为=2,所以点(0,)在☉O上,正确;
D项,点(,0)到☉O的圆心(1,0)的距离为-1<2,所以点(,0)在☉O内,错误.
故选C.
13.B 由题意,得Δ=4-4a<0,则a>1,∴点A在☉O外.
14.B 如图图,
∵AD=2,AE=AF=,AB=3,
∴AB>AE>AD,
∴当故选B.
15.316.9或2 分为两种情况:
(1)如图图①,当点P在☉O内时,PA=11,PB=7,则AB=18,因而半径是9;
(2)如图图②,当点P在☉O外时,PC=11,PD=7,则CD=4,因而半径是2.
故此圆的半径为9或2.
17.解:取AC的中点O,连接BO,DO,如图图.
∵∠ABC=∠ADC=90°,
∴BO,DO分别是Rt△ABC,Rt△ADC斜边上的中线,
∴BO=AC,DO=AC,
则BO=DO=AO=CO=AC,
∴四边形ABCD的四个顶点都在以AC为直径的圆上.
18.解:连接OD.
因为AB是☉O的直径,OD是☉O的半径,
AB=2DE,
所以OD=DE,所以∠DOE=∠E=18°,
所以∠ODC=∠DOE+∠E=36°.
因为OC=OD,所以∠C=∠ODC=36°,
所以∠AOC=∠C+∠E=36°+18°=54°.
19.54 如图图,连接EC,ED.
∵DE=DB,∴∠DEB=∠ABC=24°,
∴∠EDC=∠DEB+∠DBA=48°.
∵EC=ED,∴∠ECD=∠EDC=48°,
∴∠CED=84°,
∴∠CEB=84°+24°=108°.
∵EC=EA,
∴∠ECA=∠CAE,
∴∠CAE=∠CEB=54°.
20.a=b=c 如图图,连接OA,OD,OM.
∵四边形ABOC,DEOF,HMNO均为矩形,
∴OA=BC,OD=EF,OM=HN.
∵OA,OD,OM均为半圆O的半径,
∴OA=OD=OM,
∴BC=EF=HN,即a=b=c.
知识点 1 圆的定义
1.如图,平面内有两点O和A,以下列语句画圆,画出的圆是唯一确定的是 ( )
A.以点O为圆心画圆
B.以OA的长为半径画圆
C.画圆使它经过点A
D.以点O为圆心,OA的长为半径画圆
2.在同一平面内,到点O的距离等于8的所有点组成的图形是 .
知识点 2 点与圆的位置关系
3.☉O的半径为5 cm,点A到圆心O的距离OA为3 cm,则点A与☉O的位置关系为 ( )
A.点A在圆上 B.点A在圆内
C.点A在圆外 D.无法确定
4.若☉O的直径为20 cm,有一点A(点A与圆心O不重合)在☉O内,则线段OA长的取值范围是( )
A.OA>20 cm B.OA>10 cm
C.0 cm
A.在☉A内 B.在☉A上
C.在☉A外 D.不能确定
6.如图所示,边长为1的正方形ABCD的对角线相交于点O,以点A为圆心,1为半径画圆,则点O,B,C,D中,点 在圆内,点 在圆上,点 在圆外.
7.已知☉O的半径为5 cm,A为线段OP的中点,当OP满足下列条件时,分别指出点A与☉O的位置关系.
(1)OP=8 cm;(2)OP=10 cm;(3)OP=12 cm.
知识点 3 与圆有关的概念
8.如图所示,AB是圆的直径,则图中的弦有 条,分别是 ,劣弧有
条,分别是 .以A为一个端点的优弧有 条,分别是 .
9.有下列说法:①直径是弦;②弦是直径;③半径相等的两个半圆是等弧;④长度相等的两条弧是等弧;⑤半圆是弧,但弧不一定是半圆.其中说法正确的有 ( )
A.1个 B.2个 C.3个 D.4个
10.已知:如图,在☉O中,AB为弦,C,D两点在弦AB上,且AC=BD.
求证:△OAC≌△OBD.
11.[教材例1变式] 如图,菱形ABCD的对角线AC,BD相交于点O,E,F,G,H分别是AB,BC,CD,DA的中点,点E,F,G,H在以点O为圆心的同一个圆上吗 为什么
12.在平面直角坐标系中,☉O的圆心为(1,0),半径为2,则下面各点在☉O上的是 ( )
A.(2,0) B.(0,2) C.(0,) D.(,0)
13.已知☉O的半径为1,点A到圆心O的距离为a.若关于x的方程x2-2x+a=0不存在实数根,则点A与☉O的位置关系是 ( )
A.点A在☉O上 B.点A在☉O外
C.点A在☉O内 D.无法确定
14.如图,在网格中(每个小正方形的边长均为1个单位)选取9个格点.若以点A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为( )
A.2
16.若点P到圆上一点的最大距离为11,最小距离为7,则此圆的半径为 .
17.[教材练习第3题变式] 我们知道矩形的四个顶点都在以矩形对角线交点为圆心,对角线长度的一半为半径的圆上.如图所示,现有四边形ABCD,其中∠B=∠D=90°,试说明四边形ABCD的四个顶点都在以AC为直径的圆上.
18.如图所示,AB是☉O的直径,CD是☉O的弦,AB,CD的延长线相交于点E,已知AB=2DE,∠E=18°,求∠AOC的度数.
19.如图0,已知过A,C,D三点的圆的圆心为点E,过B,E,F三点的圆的圆心为点D.如图果∠ABC=24°,那么∠CAE= °.
0
20.如图1,点A,D,G,M在半圆O上,四边形ABOC,DEOF,HMNO均为矩形.设BC=a,EF=b,HN=c,则a,b,c的大小关系是 .
1
答案
1.D
2.以点O为圆心,以8为半径的圆
3.B 点A到圆心的距离小于圆的半径,所以点A在圆的内部.故选B.
4.D 若点在圆内,则点到圆心的距离小于圆的半径.
5.A ∵圆心A的坐标是(1,2),点P的坐标是(5,2),
∴AP=4<5,∴点P在☉A内.
故选A.
6.O B,D C ∵四边形ABCD为正方形,∴AC⊥BD,OA=OB=OC=OD.
设OA=OB=x,
由勾股定理,得OA2+OB2=AB2,
即x2+x2=12,
解得x=(负值已舍去),
∴OA=<1,AC=>1.
即点O在圆内,点C在圆外.
∵AD=AB=1,∴点B,D在圆上.
7.解:(1)当OP=8 cm时,OA=OP=4 cm.
又☉O的半径为5 cm,所以点A在☉O内.
(2)当OP=10 cm时,OA=OP=5 cm.
又☉O的半径为5 cm,所以点A在☉O上.
(3)当OP=12 cm时,OA=OP=6 cm.
又☉O的半径为5 cm,所以点A在☉O外.
8.2 弦CD,弦AB 5 ,,,,
2 ,
本题考查对弦与劣弧、优弧的概念的理解.
9.C 正确的有①③⑤.
10.证明:∵OA=OB,
∴∠A=∠B.
在△OAC和△OBD中,
∵
∴△OAC≌△OBD(SAS).
11.解:点E,F,G,H在以点O为圆心的同一个圆上.理由:如图图,连接EO,HO,FO,GO.
∵四边形ABCD是菱形,
∴AC⊥BD,AB=BC=DC=AD,
∴∠AOB=∠AOD=∠BOC=∠COD=90°.
∵E,F,G,H分别是AB,BC,CD,DA的中点,
∴EO=FO=HO=GO=AB,
∴点E,F,G,H在以点O为圆心的同一个圆上.
12.C A项,点(2,0)到☉O的圆心(1,0)的距离为2-1=1<2,所以点(2,0)在☉O内,错误;
B项,点(0,2)到☉O的圆心(1,0)的距离为=>2,所以点(0,2)在☉O外,错误;
C项,点(0,)到☉O的圆心(1,0)的距离为=2,所以点(0,)在☉O上,正确;
D项,点(,0)到☉O的圆心(1,0)的距离为-1<2,所以点(,0)在☉O内,错误.
故选C.
13.B 由题意,得Δ=4-4a<0,则a>1,∴点A在☉O外.
14.B 如图图,
∵AD=2,AE=AF=,AB=3,
∴AB>AE>AD,
∴当
15.3
(1)如图图①,当点P在☉O内时,PA=11,PB=7,则AB=18,因而半径是9;
(2)如图图②,当点P在☉O外时,PC=11,PD=7,则CD=4,因而半径是2.
故此圆的半径为9或2.
17.解:取AC的中点O,连接BO,DO,如图图.
∵∠ABC=∠ADC=90°,
∴BO,DO分别是Rt△ABC,Rt△ADC斜边上的中线,
∴BO=AC,DO=AC,
则BO=DO=AO=CO=AC,
∴四边形ABCD的四个顶点都在以AC为直径的圆上.
18.解:连接OD.
因为AB是☉O的直径,OD是☉O的半径,
AB=2DE,
所以OD=DE,所以∠DOE=∠E=18°,
所以∠ODC=∠DOE+∠E=36°.
因为OC=OD,所以∠C=∠ODC=36°,
所以∠AOC=∠C+∠E=36°+18°=54°.
19.54 如图图,连接EC,ED.
∵DE=DB,∴∠DEB=∠ABC=24°,
∴∠EDC=∠DEB+∠DBA=48°.
∵EC=ED,∴∠ECD=∠EDC=48°,
∴∠CED=84°,
∴∠CEB=84°+24°=108°.
∵EC=EA,
∴∠ECA=∠CAE,
∴∠CAE=∠CEB=54°.
20.a=b=c 如图图,连接OA,OD,OM.
∵四边形ABOC,DEOF,HMNO均为矩形,
∴OA=BC,OD=EF,OM=HN.
∵OA,OD,OM均为半圆O的半径,
∴OA=OD=OM,
∴BC=EF=HN,即a=b=c.
