沪科版数学九年级下册同步课时练习:24.2 第2课时 垂径分弦(word版含答案)
文档属性
| 名称 | 沪科版数学九年级下册同步课时练习:24.2 第2课时 垂径分弦(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 285.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 00:00:00 | ||
图片预览


文档简介
第2课时 垂径分弦
知识点 1 圆的轴对称性
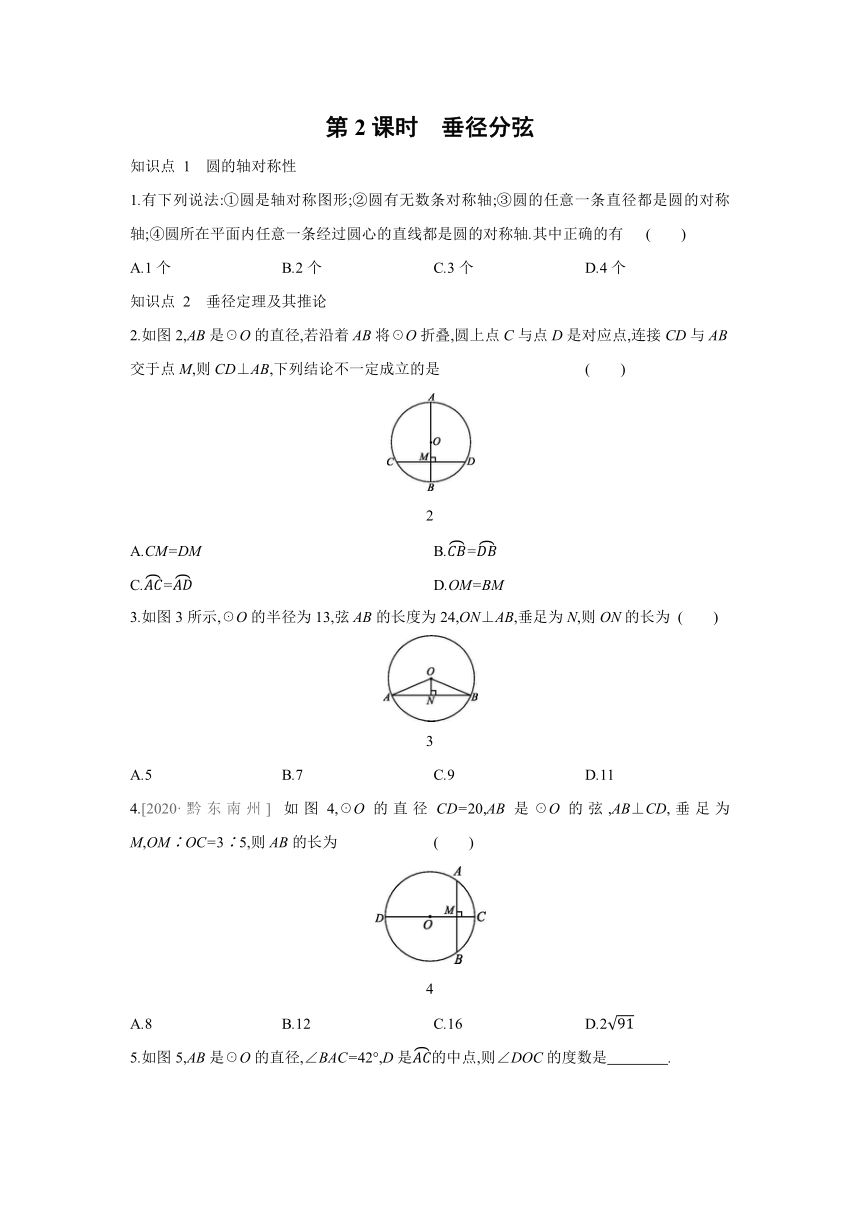
1.有下列说法:①圆是轴对称图形;②圆有无数条对称轴;③圆的任意一条直径都是圆的对称轴;④圆所在平面内任意一条经过圆心的直线都是圆的对称轴.其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
知识点 2 垂径定理及其推论
2.如图2,AB是☉O的直径,若沿着AB将☉O折叠,圆上点C与点D是对应点,连接CD与AB交于点M,则CD⊥AB,下列结论不一定成立的是 ( )
2
A.CM=DM B.=
C.= D.OM=BM
3.如图3所示,☉O的半径为13,弦AB的长度为24,ON⊥AB,垂足为N,则ON的长为 ( )
3
A.5 B.7 C.9 D.11
4.[2020·黔东南州] 如图4,☉O的直径CD=20,AB是☉O的弦,AB⊥CD,垂足为M,OM∶OC=3∶5,则AB的长为 ( )
4
A.8 B.12 C.16 D.2
5.如图5,AB是☉O的直径,∠BAC=42°,D是的中点,则∠DOC的度数是 .
5
6.如图6所示,AB是☉O的直径,弦CD⊥AB于点H,∠A=30°,CD=2,则☉O的半径是 .
6
7.如图7,AB是☉O的直径,弦CD⊥AB于点P,CD=10 cm,AP∶PB=1∶5,求☉O的半径.
7
知识点 3 垂径定理的实际应用
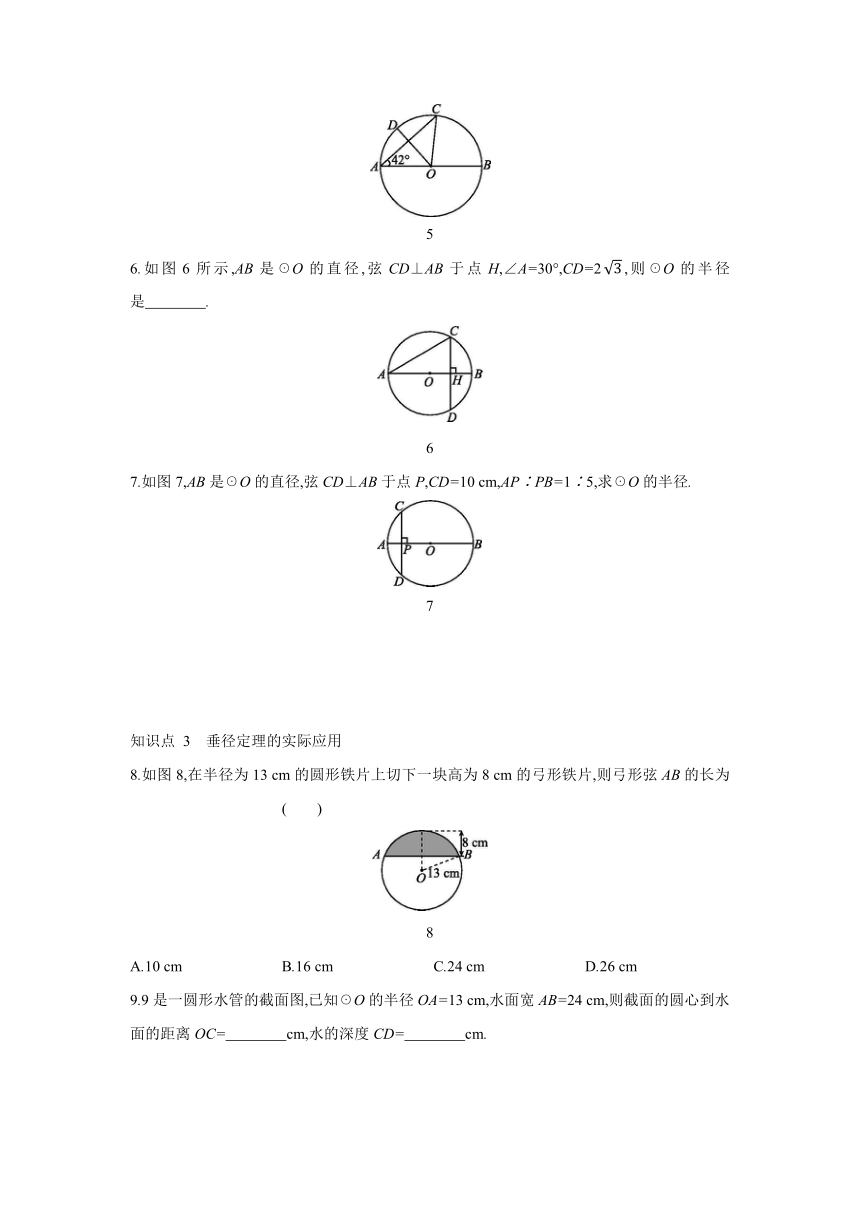
8.如图8,在半径为13 cm的圆形铁片上切下一块高为8 cm的弓形铁片,则弓形弦AB的长为 ( )
8
A.10 cm B.16 cm C.24 cm D.26 cm
9.9是一圆形水管的截面图,已知☉O的半径OA=13 cm,水面宽AB=24 cm,则截面的圆心到水面的距离OC= cm,水的深度CD= cm.
9
10.0是一个隧道的截面,如图果路面宽AB为8米,净高CD为8米,求这个隧道所在圆的半径OA的长.
0
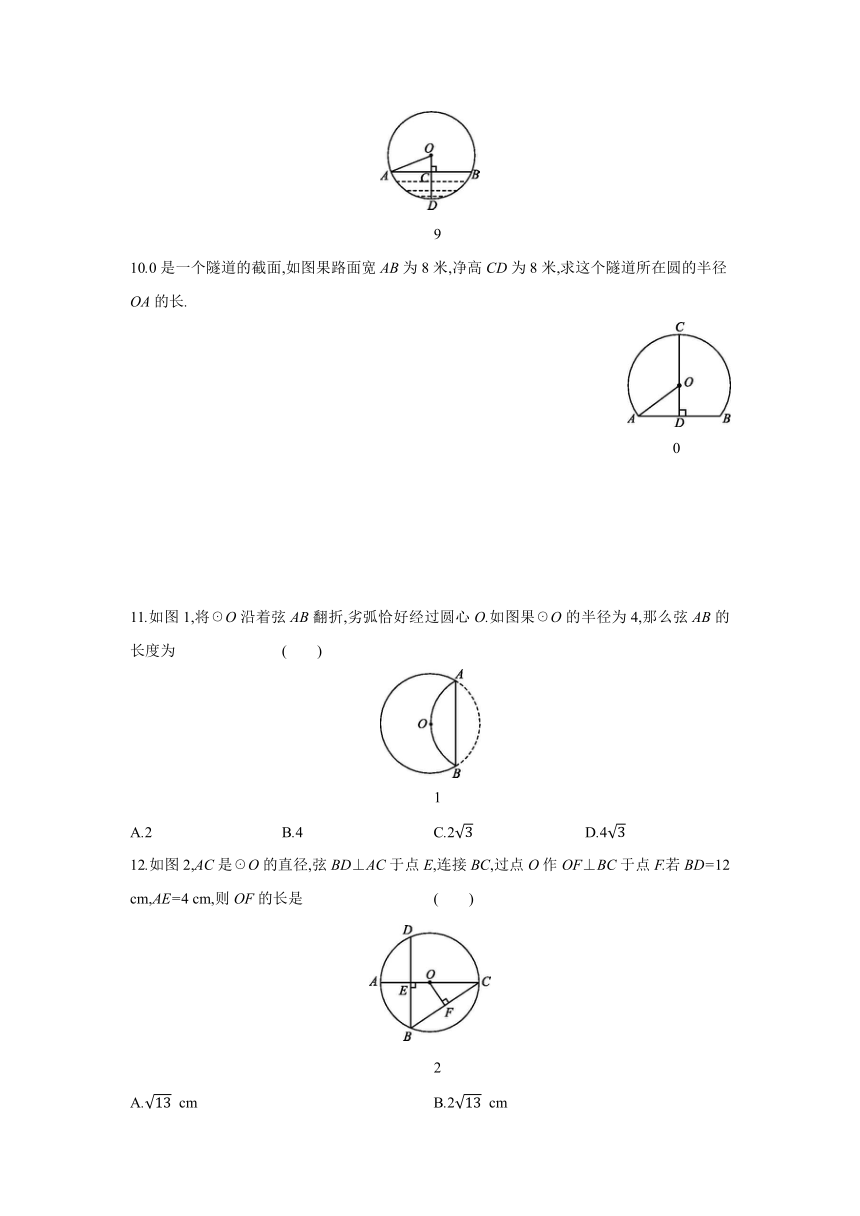
11.如图1,将☉O沿着弦AB翻折,劣弧恰好经过圆心O.如图果☉O的半径为4,那么弦AB的长度为 ( )
1
A.2 B.4 C.2 D.4
12.如图2,AC是☉O的直径,弦BD⊥AC于点E,连接BC,过点O作OF⊥BC于点F.若BD=12 cm,AE=4 cm,则OF的长是 ( )
2
A. cm B.2 cm
C. cm D.3 cm
13.已知☉O的直径CD=10 cm,AB是☉O的弦,AB⊥CD,垂足为M,且AB=8 cm,则AC的长为 ( )
A.2 cm B.4 cm
C.2 cm或4 cm D.2 cm或4 cm
14.如图3所示,AB为☉O的直径,弦CD交AB于点E.已知OE=2,BE=1,∠AEC=45°,则CD= .
3
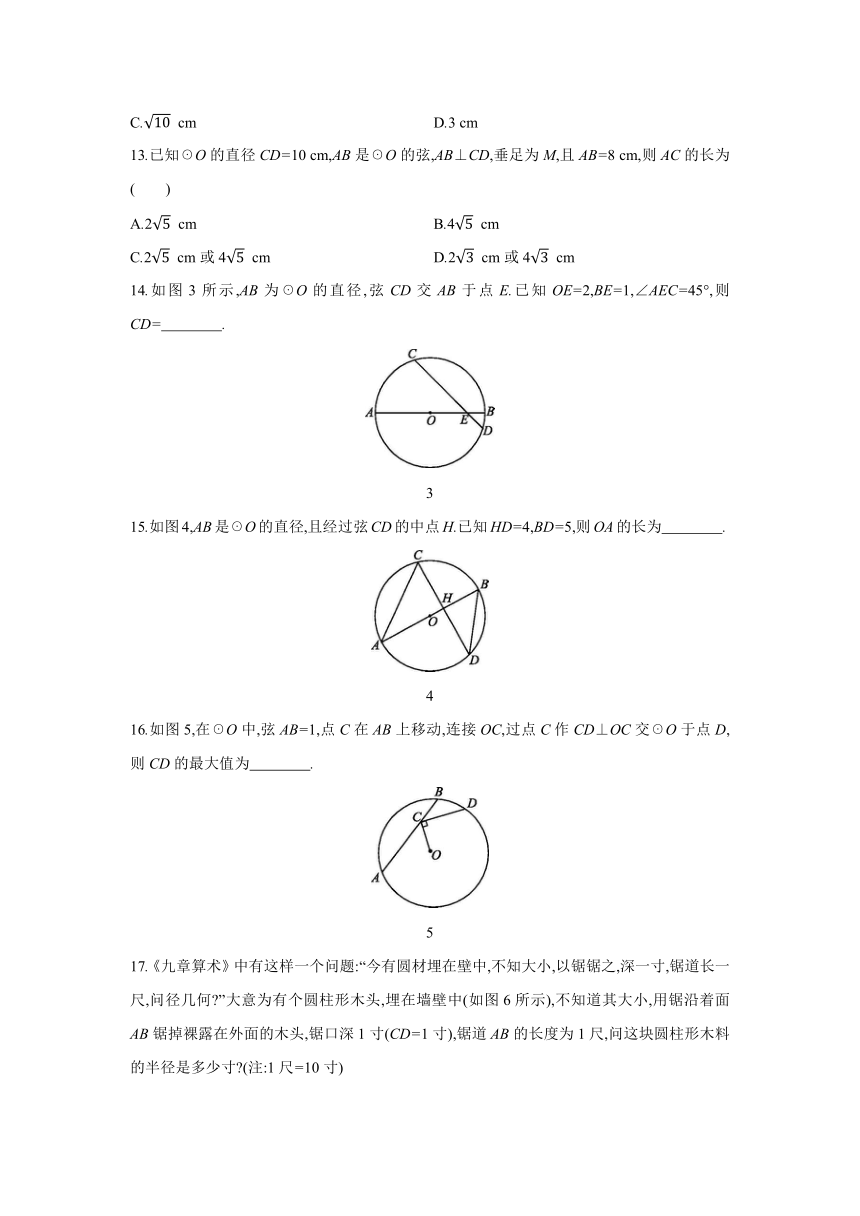
15.如图4,AB是☉O的直径,且经过弦CD的中点H.已知HD=4,BD=5,则OA的长为 .
4
16.如图5,在☉O中,弦AB=1,点C在AB上移动,连接OC,过点C作CD⊥OC交☉O于点D,则CD的最大值为 .
5
17.《九章算术》中有这样一个问题:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何 ”大意为有个圆柱形木头,埋在墙壁中(如图6所示),不知道其大小,用锯沿着面AB锯掉裸露在外面的木头,锯口深1寸(CD=1寸),锯道AB的长度为1尺,问这块圆柱形木料的半径是多少寸 (注:1尺=10寸)
6
18.如图7,☉O的半径为20,A是☉O上一点,以OA为对角线作矩形OBAC,且OC=12,直线BC与☉O交于D,E两点,求CE-BD的值.
7
答案
1.C ①②④正确.对称轴是直线,而圆的直径是线段,所以③错误.
2.D 由于圆是轴对称图形,通过折叠可知CM=DM,与重合,与重合,故只有D项不一定成立.
3.A ∵ON⊥AB,
∴AN=BN=AB=12,
∴ON===5.
4.C 如图图,连接OA.
∵☉O的直径CD=20,OM∶OC=3∶5,
∴OA=OC=10,OM=6.
∵AB⊥CD,
∴AM===8,
∴AB=2AM=16.
故选C.
5.48° ∵D是的中点,
∴OD⊥AC,∴∠DOC+∠ACO=90°.
∵OA=OC,∴∠ACO=∠A=42°,
∴∠DOC=90°-∠ACO=48°.
6.2 如图图,连接OC,则OA=OC,
∴∠A=∠ACO=30°,
∴∠COH=60°.
∵AB⊥CD,CD=2,
∴CH=,∴OH=1,∴OC=2.
7.解:连接CO,如图图.
设AP=x cm,则PB=5x cm,AO=(x+5x)=×6x=3x(cm),PO=3x-x=2x(cm).
∵AB⊥CD,
∴CP=×10=5(cm).
在△CPO中,52+(2x)2=(3x)2,
解得x1=,x2=-(舍去).
∴AO=3 cm.
即☉O的半径为3 cm.
8.C 如图图,过点O作OD⊥AB于点C,交☉O于点D.
∵CD=8 cm,OD=13 cm,∴OC=5 cm.
又∵OB=13 cm,
∴在Rt△BCO中,BC==12 cm.
∵OD⊥AB,
∴AB=2BC=24 cm.
9.5 8 ∵☉O的半径OA=13 cm,水面宽AB=24 cm,OD⊥AB,∴OD=OA=13 cm,AC=AB=12 cm.在Rt△AOC中,OC===5(cm),
∴CD=OD-OC=13-5=8(cm).
10.解:设这个隧道所在圆的半径OA的长是x米,则OD=(8-x)米.
∵CD⊥AB,AB=8米,
∴AD=4米.
在Rt△AOD中,OA2=AD2+OD2,
即x2=42+(8-x)2,解得x=5,
即这个隧道所在圆的半径OA的长是5米.
11.D 如图图,过点O作OC⊥AB于点D,交☉O于点C,连接OA.
由垂径定理,得AD=BD.
由折叠的性质,得OD=CD.
在Rt△OAD中,OD=CD=OC=2,OA=4,
∴根据勾股定理,得AD===2,
∴AB=2AD=4.
故选D.
12.A 如图图,连接OB.
∵AC是☉O的直径,弦BD⊥AC,BD=12 cm,
∴BE=BD=6 cm.
在Rt△OEB中,OB2=OE2+BE2,
即OB2=(OB-4)2+62,解得OB= cm.
则EC=AC-AE=9(cm).
在Rt△BEC中,BC==3(cm).
∵OF⊥BC,∴CF=BC= cm,
∴OF==(cm).
13.C 连接AC,AO.
∵☉O的直径CD=10 cm,AB⊥CD,AB=8 cm,
∴AM=AB=×8=4(cm),OD=OC=5 cm.
当点C的位置如图图①所示时,
∵OA=5 cm,AM=4 cm,CD⊥AB,
∴OM===3(cm),
∴CM=OC+OM=5+3=8(cm),
∴AC===4(cm);
当点C的位置如图图②所示时,同理可得OM=3 cm.
∵OC=5 cm,
∴CM=5-3=2(cm).
在Rt△AMC中,AC===2(cm).
综上,AC的长为4 cm或2 cm.
故选C.
14.2 如图图,过点O作OH⊥CD于点H,连接OC.
∵OH⊥CD,∴CH=DH,∠OHE=90°.
∵∠OEH=45°,OE=2,
∴OH=HE=.
∵OC=OB=OE+BE=3,
∴CH==,
∴CD=2CH=2.故答案为2.
15. 如图图,连接OD.
∵AB是☉O的直径,且经过弦CD的中点H,
∴CH=HD,AB⊥CD,
∴∠BHD=90°.
∵HD=4,BD=5,∴BH=3.
设OA=x,则OH=x-3.
在Rt△OHD中,OD2=HD2+OH2,
即x2=42+(x-3)2,
解得x=,即OA=.
16. 连接OD,如图图.
∵CD⊥OC,∴∠DCO=90°,
∴CD==.
当OC最小时,CD最大.
∵当OC⊥AB时,OC最小,
此时D,B两点重合,
∴CD=CB=AB=×1=,即CD的最大值为.
17.解:如图图,连接AO,DO.
由题意知C,D,O三点共线,AB⊥CD,
∴AD=BD.
∵AB=10,∴AD=5.
在Rt△AOD中,
∵OA2=OD2+AD2,
∴OA2=(OA-1)2+52,解得OA=13.
答:这块圆柱形木料的半径是13寸.
18.解:如图图,过点O作OF⊥DE于点F,
则DF=EF.
在矩形ABOC中,OA=20,
∴BC=OA=20,∠BOC=90°.
在Rt△BOC中,OC=12,
∴cos∠OCB===.
在Rt△OCF中,cos∠OCF=cos∠OCB==,
∴CF=,则BF=BC-CF=,
∴CE-BD=(EF-CF)-(DF-BF)=BF-CF=.
知识点 1 圆的轴对称性
1.有下列说法:①圆是轴对称图形;②圆有无数条对称轴;③圆的任意一条直径都是圆的对称轴;④圆所在平面内任意一条经过圆心的直线都是圆的对称轴.其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
知识点 2 垂径定理及其推论
2.如图2,AB是☉O的直径,若沿着AB将☉O折叠,圆上点C与点D是对应点,连接CD与AB交于点M,则CD⊥AB,下列结论不一定成立的是 ( )
2
A.CM=DM B.=
C.= D.OM=BM
3.如图3所示,☉O的半径为13,弦AB的长度为24,ON⊥AB,垂足为N,则ON的长为 ( )
3
A.5 B.7 C.9 D.11
4.[2020·黔东南州] 如图4,☉O的直径CD=20,AB是☉O的弦,AB⊥CD,垂足为M,OM∶OC=3∶5,则AB的长为 ( )
4
A.8 B.12 C.16 D.2
5.如图5,AB是☉O的直径,∠BAC=42°,D是的中点,则∠DOC的度数是 .
5
6.如图6所示,AB是☉O的直径,弦CD⊥AB于点H,∠A=30°,CD=2,则☉O的半径是 .
6
7.如图7,AB是☉O的直径,弦CD⊥AB于点P,CD=10 cm,AP∶PB=1∶5,求☉O的半径.
7
知识点 3 垂径定理的实际应用
8.如图8,在半径为13 cm的圆形铁片上切下一块高为8 cm的弓形铁片,则弓形弦AB的长为 ( )
8
A.10 cm B.16 cm C.24 cm D.26 cm
9.9是一圆形水管的截面图,已知☉O的半径OA=13 cm,水面宽AB=24 cm,则截面的圆心到水面的距离OC= cm,水的深度CD= cm.
9
10.0是一个隧道的截面,如图果路面宽AB为8米,净高CD为8米,求这个隧道所在圆的半径OA的长.
0
11.如图1,将☉O沿着弦AB翻折,劣弧恰好经过圆心O.如图果☉O的半径为4,那么弦AB的长度为 ( )
1
A.2 B.4 C.2 D.4
12.如图2,AC是☉O的直径,弦BD⊥AC于点E,连接BC,过点O作OF⊥BC于点F.若BD=12 cm,AE=4 cm,则OF的长是 ( )
2
A. cm B.2 cm
C. cm D.3 cm
13.已知☉O的直径CD=10 cm,AB是☉O的弦,AB⊥CD,垂足为M,且AB=8 cm,则AC的长为 ( )
A.2 cm B.4 cm
C.2 cm或4 cm D.2 cm或4 cm
14.如图3所示,AB为☉O的直径,弦CD交AB于点E.已知OE=2,BE=1,∠AEC=45°,则CD= .
3
15.如图4,AB是☉O的直径,且经过弦CD的中点H.已知HD=4,BD=5,则OA的长为 .
4
16.如图5,在☉O中,弦AB=1,点C在AB上移动,连接OC,过点C作CD⊥OC交☉O于点D,则CD的最大值为 .
5
17.《九章算术》中有这样一个问题:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何 ”大意为有个圆柱形木头,埋在墙壁中(如图6所示),不知道其大小,用锯沿着面AB锯掉裸露在外面的木头,锯口深1寸(CD=1寸),锯道AB的长度为1尺,问这块圆柱形木料的半径是多少寸 (注:1尺=10寸)
6
18.如图7,☉O的半径为20,A是☉O上一点,以OA为对角线作矩形OBAC,且OC=12,直线BC与☉O交于D,E两点,求CE-BD的值.
7
答案
1.C ①②④正确.对称轴是直线,而圆的直径是线段,所以③错误.
2.D 由于圆是轴对称图形,通过折叠可知CM=DM,与重合,与重合,故只有D项不一定成立.
3.A ∵ON⊥AB,
∴AN=BN=AB=12,
∴ON===5.
4.C 如图图,连接OA.
∵☉O的直径CD=20,OM∶OC=3∶5,
∴OA=OC=10,OM=6.
∵AB⊥CD,
∴AM===8,
∴AB=2AM=16.
故选C.
5.48° ∵D是的中点,
∴OD⊥AC,∴∠DOC+∠ACO=90°.
∵OA=OC,∴∠ACO=∠A=42°,
∴∠DOC=90°-∠ACO=48°.
6.2 如图图,连接OC,则OA=OC,
∴∠A=∠ACO=30°,
∴∠COH=60°.
∵AB⊥CD,CD=2,
∴CH=,∴OH=1,∴OC=2.
7.解:连接CO,如图图.
设AP=x cm,则PB=5x cm,AO=(x+5x)=×6x=3x(cm),PO=3x-x=2x(cm).
∵AB⊥CD,
∴CP=×10=5(cm).
在△CPO中,52+(2x)2=(3x)2,
解得x1=,x2=-(舍去).
∴AO=3 cm.
即☉O的半径为3 cm.
8.C 如图图,过点O作OD⊥AB于点C,交☉O于点D.
∵CD=8 cm,OD=13 cm,∴OC=5 cm.
又∵OB=13 cm,
∴在Rt△BCO中,BC==12 cm.
∵OD⊥AB,
∴AB=2BC=24 cm.
9.5 8 ∵☉O的半径OA=13 cm,水面宽AB=24 cm,OD⊥AB,∴OD=OA=13 cm,AC=AB=12 cm.在Rt△AOC中,OC===5(cm),
∴CD=OD-OC=13-5=8(cm).
10.解:设这个隧道所在圆的半径OA的长是x米,则OD=(8-x)米.
∵CD⊥AB,AB=8米,
∴AD=4米.
在Rt△AOD中,OA2=AD2+OD2,
即x2=42+(8-x)2,解得x=5,
即这个隧道所在圆的半径OA的长是5米.
11.D 如图图,过点O作OC⊥AB于点D,交☉O于点C,连接OA.
由垂径定理,得AD=BD.
由折叠的性质,得OD=CD.
在Rt△OAD中,OD=CD=OC=2,OA=4,
∴根据勾股定理,得AD===2,
∴AB=2AD=4.
故选D.
12.A 如图图,连接OB.
∵AC是☉O的直径,弦BD⊥AC,BD=12 cm,
∴BE=BD=6 cm.
在Rt△OEB中,OB2=OE2+BE2,
即OB2=(OB-4)2+62,解得OB= cm.
则EC=AC-AE=9(cm).
在Rt△BEC中,BC==3(cm).
∵OF⊥BC,∴CF=BC= cm,
∴OF==(cm).
13.C 连接AC,AO.
∵☉O的直径CD=10 cm,AB⊥CD,AB=8 cm,
∴AM=AB=×8=4(cm),OD=OC=5 cm.
当点C的位置如图图①所示时,
∵OA=5 cm,AM=4 cm,CD⊥AB,
∴OM===3(cm),
∴CM=OC+OM=5+3=8(cm),
∴AC===4(cm);
当点C的位置如图图②所示时,同理可得OM=3 cm.
∵OC=5 cm,
∴CM=5-3=2(cm).
在Rt△AMC中,AC===2(cm).
综上,AC的长为4 cm或2 cm.
故选C.
14.2 如图图,过点O作OH⊥CD于点H,连接OC.
∵OH⊥CD,∴CH=DH,∠OHE=90°.
∵∠OEH=45°,OE=2,
∴OH=HE=.
∵OC=OB=OE+BE=3,
∴CH==,
∴CD=2CH=2.故答案为2.
15. 如图图,连接OD.
∵AB是☉O的直径,且经过弦CD的中点H,
∴CH=HD,AB⊥CD,
∴∠BHD=90°.
∵HD=4,BD=5,∴BH=3.
设OA=x,则OH=x-3.
在Rt△OHD中,OD2=HD2+OH2,
即x2=42+(x-3)2,
解得x=,即OA=.
16. 连接OD,如图图.
∵CD⊥OC,∴∠DCO=90°,
∴CD==.
当OC最小时,CD最大.
∵当OC⊥AB时,OC最小,
此时D,B两点重合,
∴CD=CB=AB=×1=,即CD的最大值为.
17.解:如图图,连接AO,DO.
由题意知C,D,O三点共线,AB⊥CD,
∴AD=BD.
∵AB=10,∴AD=5.
在Rt△AOD中,
∵OA2=OD2+AD2,
∴OA2=(OA-1)2+52,解得OA=13.
答:这块圆柱形木料的半径是13寸.
18.解:如图图,过点O作OF⊥DE于点F,
则DF=EF.
在矩形ABOC中,OA=20,
∴BC=OA=20,∠BOC=90°.
在Rt△BOC中,OC=12,
∴cos∠OCB===.
在Rt△OCF中,cos∠OCF=cos∠OCB==,
∴CF=,则BF=BC-CF=,
∴CE-BD=(EF-CF)-(DF-BF)=BF-CF=.
