沪科版数学九年级下册同步课时练习:24.2 第3课时 圆心角、弧、弦、弦心距间的关系(word版含答案)
文档属性
| 名称 | 沪科版数学九年级下册同步课时练习:24.2 第3课时 圆心角、弧、弦、弦心距间的关系(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 230.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 00:00:00 | ||
图片预览


文档简介
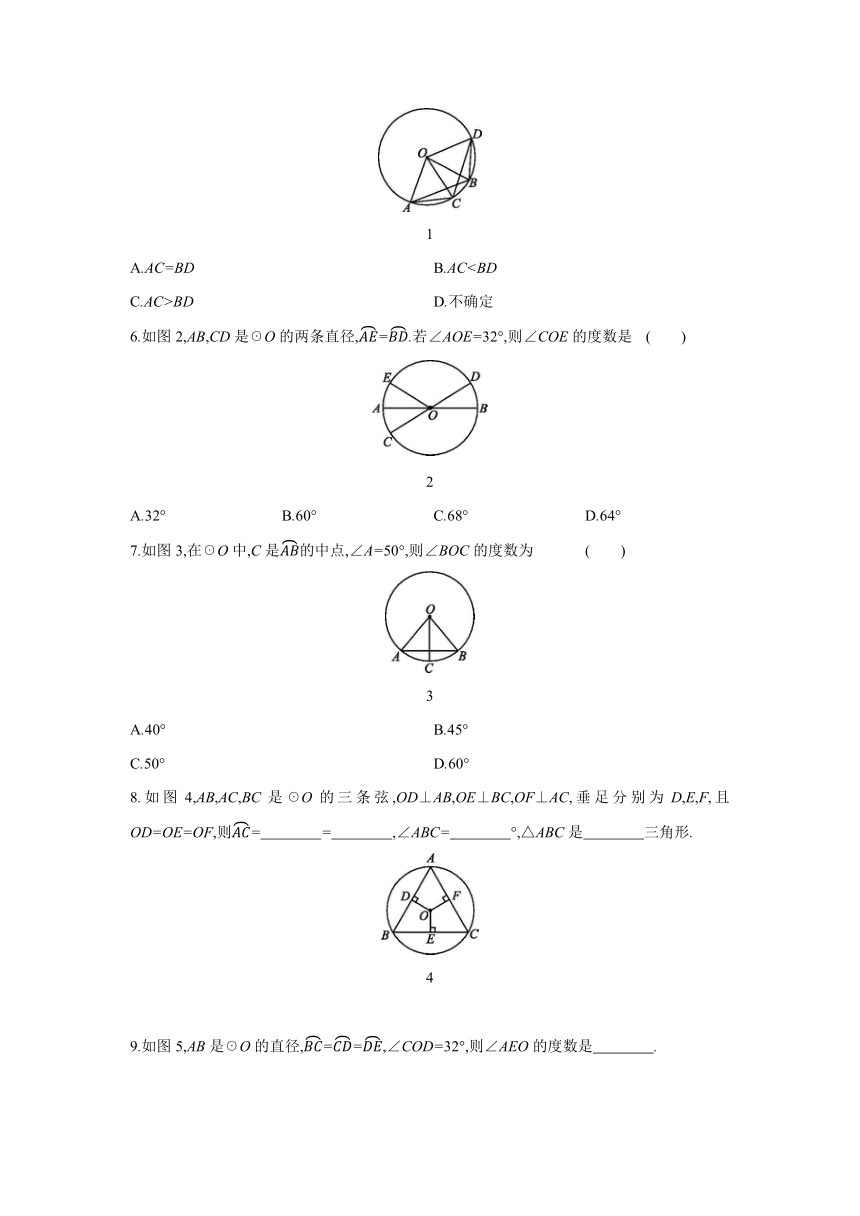
第3课时 圆心角、弧、弦、弦心距间的关系
知识点 1 圆心角的概念
1.下列图中的四个角,为圆心角的是 ( )
8
2.如图9,已知AB是☉O的直径,PA=PB,∠P=60°,则弧CD所对的圆心角的度数为 .
9
知识点 2 圆心角、弧、弦、弦心距间的关系
3.如图0,已知AB,CD是☉O的两条弦,OE,OF分别为AB,CD的弦心距.
0
(1)∵∠AOB=∠COD,∴AB= ,= ,OE= ;
(2)∵AB=CD,∴= , =∠BOC,OE= .
4.如图果两个圆心角相等,那么 ( )
A.这两个圆心角所对的弦相等
B.这两个圆心角所对的弧相等
C.这两个圆心角所对弦的弦心距相等
D.以上说法都不对
5.如图1,在☉O中,已知=,则AC与BD的关系是 ( )
1
A.AC=BD B.ACC.AC>BD D.不确定
6.如图2,AB,CD是☉O的两条直径,=.若∠AOE=32°,则∠COE的度数是 ( )
2
A.32° B.60° C.68° D.64°
7.如图3,在☉O中,C是的中点,∠A=50°,则∠BOC的度数为 ( )
3
A.40° B.45°
C.50° D.60°
8.如图4,AB,AC,BC是☉O的三条弦,OD⊥AB,OE⊥BC,OF⊥AC,垂足分别为D,E,F,且OD=OE=OF,则= = ,∠ABC= °,△ABC是 三角形.
4
9.如图5,AB是☉O的直径,==,∠COD=32°,则∠AEO的度数是 .
5
10.[教材例6变式] 如图6,已知AB和CD是☉O的两条直径,CE为☉O的弦,且CE∥AB.若的度数为40°,求的度数.
6
11.如图7,☉O中两条不平行的弦AB和CD的中点分别为M,N,且AB=CD.求证:∠AMN=∠CNM.
7
12.在☉O中,如图果=2,那么弦AB与弦CD之间的关系是 ( )
A.AB=2CD B.AB>2CD
C.AB<2CD D.无法确定
13.如图8,AB是☉O的直径,C,D为半圆的三等分点,CE⊥AB于点E,则∠ACE的度数为 .
8
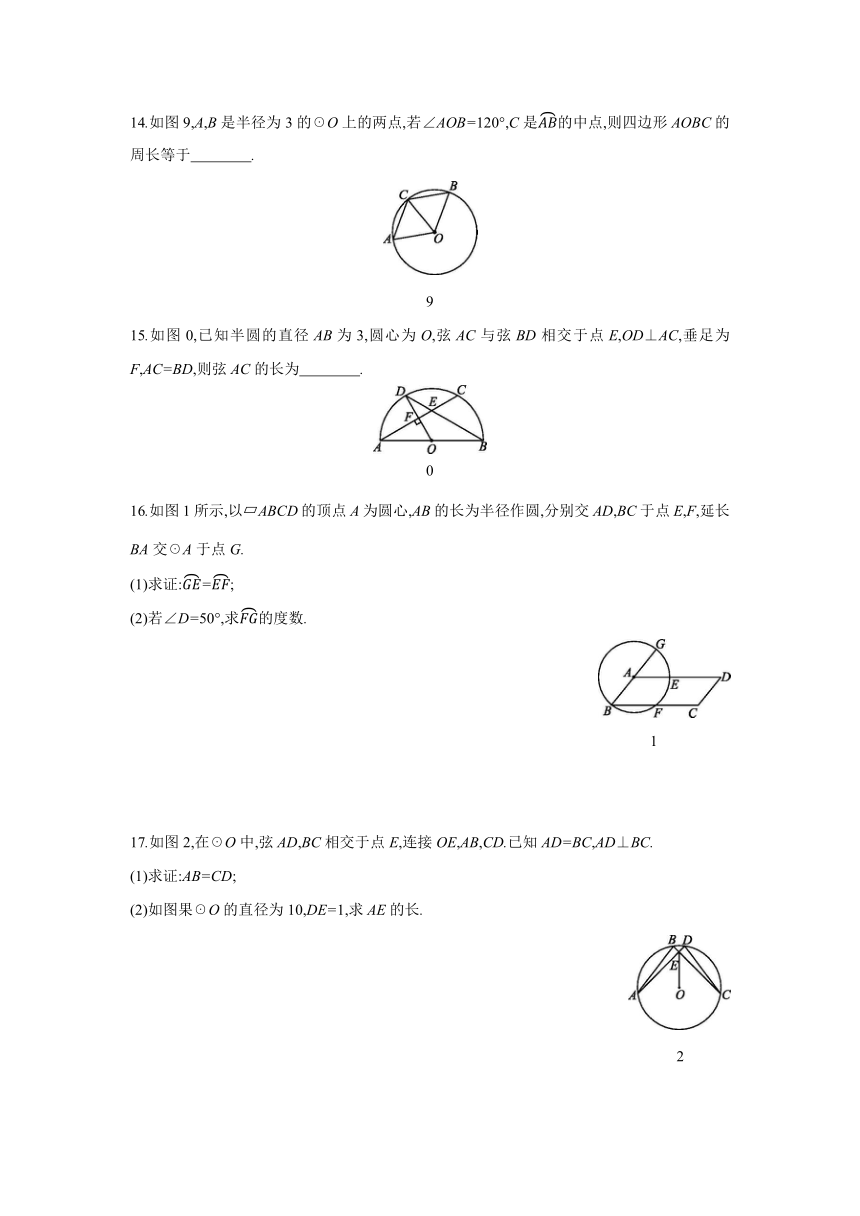
14.如图9,A,B是半径为3的☉O上的两点,若∠AOB=120°,C是的中点,则四边形AOBC的周长等于 .
9
15.如图0,已知半圆的直径AB为3,圆心为O,弦AC与弦BD相交于点E,OD⊥AC,垂足为F,AC=BD,则弦AC的长为 .
0
16.如图1所示,以 ABCD的顶点A为圆心,AB的长为半径作圆,分别交AD,BC于点E,F,延长BA交☉A于点G.
(1)求证:=;
(2)若∠D=50°,求的度数.
1
17.如图2,在☉O中,弦AD,BC相交于点E,连接OE,AB,CD.已知AD=BC,AD⊥BC.
(1)求证:AB=CD;
(2)如图果☉O的直径为10,DE=1,求AE的长.
2
18.如图3①,PC是☉O的直径,PA与PB是弦,且∠APC=∠BPC.
(1)求证:PA=PB;
(2)如图图②,如图果点P由圆上运动到圆外,且PC过圆心,是否仍有PA=PB 为什么
(3)如图图③,如图果点P由圆上运动到圆内,PA=PB还成立吗 (无需证明)
3
答案
1.D 根据圆心角的概念,圆心角的顶点必须为圆心,即可判定选项D正确.
2.60°
3.(1)CD OF (2) ∠AOD OF
4.D 在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对弦的弦心距相等.题干中没有“同圆或等圆”的条件.
5.A 6.D 7.A
8. 60 等边
9.48° ∵==,∠COD=32°,
∴∠BOC=∠EOD=∠COD=32°,
∴∠AOE=180°-∠EOD-∠COD-∠BOC=84°.
又∵OA=OE,∴∠AEO=∠OAE,
∴∠AEO=×(180°-84°)=48°.
10.解:连接OE.
∵的度数为40°,∴∠COE=40°.
∵OC=OE,
∴∠OEC=×(180°-40°)=70°.
∵CE∥AB,
∴∠AOE=∠OEC=70°,
∴的度数为70°.
11.证明:连接OM,ON,如图图.
∵M,N分别为AB,CD的中点,
∴OM⊥AB,ON⊥CD,
∴∠AMO=∠CNO=90°.
∵AB=CD,
∴OM=ON,
∴∠OMN=∠ONM,
∴∠AMN=∠CNM.
12.C 利用圆的旋转对称性,使点C与点A重合,则D为的中点,这样有CD=BD.在△ABD中,利用三角形三边之间的关系有AB13.30° 如图图,连接OC.
∵在☉O中,==,
∴∠AOC=∠COD=∠DOB=60°.
∵OA=OC,
∴△AOC是等边三角形,
∴∠A=60°.
∵CE⊥OA,∴∠AEC=90°,
∴∠ACE=90°-60°=30°.
14.12 ∵C是的中点,∴=,
∴∠AOC=∠BOC,而∠AOB=120°,∴∠AOC=∠BOC=60°,∴△AOC和△BOC都是等边三角形,
即OA=OB=CA=CB=3,
∴四边形AOBC的周长等于12.
15. 如图图,连接OC.
∵OD⊥AC,
∴=,∠AFO=90°.
又∵AC=BD,
∴=,
即+=+,
∴=,
∴==,
∴∠AOD=∠DOC=∠BOC=60°.
∵AB=3,
∴AO=BO=,
∴AF=AOsin∠AOF=×=,
则AC=2AF=.
16.解:(1)证明:如图图,连接AF.
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EAF=∠AFB,∠GAE=∠B.
∵AB=AF,∴∠B=∠AFB,
∴∠EAF=∠GAE,∴=.
(2)∵四边形ABCD是平行四边形,
∴∠B=∠D=50°,∴∠GAE=∠EAF=50°,
则∠GAF=100°,
∴的度数为100°.
17.解:(1)证明:∵AD=BC,∴=,
∴-=-,即=,
∴AB=CD.
(2)如图图,过点O作OF⊥AD于点F,OG⊥BC于点G,连接OA.
∵AD=BC,
∴OF=OG.
又∵AD⊥BC,
∴四边形OFEG是正方形,
∴OF=EF.
设OF=EF=x,则AF=FD=x+1.
在Rt△OAF中,由勾股定理,得
x2+(x+1)2=52,解得x=3.
则AF=3+1=4,
∴AE=AF+EF=7.
18.解:(1)证明:过点O作OE⊥PA于点E,
OF⊥PB于点F,则有∠PEO=∠PFO=90°.
又∵∠APC=∠BPC,OP=OP,
∴△POE≌△POF,
∴OE=OF,∴PA=PB.
(2)仍有PA=PB.理由如图下:
过点O作OE⊥PA于点E,OF⊥PB于点F,同(1)可证△POE≌△POF,
∴PE=PF,OE=OF.
连接OA,OB,在Rt△AOE与Rt△BOF中,
AE=,BF=.
∵OA=OB,OE=OF,∴AE=BF,
∴PE+AE=PF+BF,即PA=PB.
(3)成立.
知识点 1 圆心角的概念
1.下列图中的四个角,为圆心角的是 ( )
8
2.如图9,已知AB是☉O的直径,PA=PB,∠P=60°,则弧CD所对的圆心角的度数为 .
9
知识点 2 圆心角、弧、弦、弦心距间的关系
3.如图0,已知AB,CD是☉O的两条弦,OE,OF分别为AB,CD的弦心距.
0
(1)∵∠AOB=∠COD,∴AB= ,= ,OE= ;
(2)∵AB=CD,∴= , =∠BOC,OE= .
4.如图果两个圆心角相等,那么 ( )
A.这两个圆心角所对的弦相等
B.这两个圆心角所对的弧相等
C.这两个圆心角所对弦的弦心距相等
D.以上说法都不对
5.如图1,在☉O中,已知=,则AC与BD的关系是 ( )
1
A.AC=BD B.AC
6.如图2,AB,CD是☉O的两条直径,=.若∠AOE=32°,则∠COE的度数是 ( )
2
A.32° B.60° C.68° D.64°
7.如图3,在☉O中,C是的中点,∠A=50°,则∠BOC的度数为 ( )
3
A.40° B.45°
C.50° D.60°
8.如图4,AB,AC,BC是☉O的三条弦,OD⊥AB,OE⊥BC,OF⊥AC,垂足分别为D,E,F,且OD=OE=OF,则= = ,∠ABC= °,△ABC是 三角形.
4
9.如图5,AB是☉O的直径,==,∠COD=32°,则∠AEO的度数是 .
5
10.[教材例6变式] 如图6,已知AB和CD是☉O的两条直径,CE为☉O的弦,且CE∥AB.若的度数为40°,求的度数.
6
11.如图7,☉O中两条不平行的弦AB和CD的中点分别为M,N,且AB=CD.求证:∠AMN=∠CNM.
7
12.在☉O中,如图果=2,那么弦AB与弦CD之间的关系是 ( )
A.AB=2CD B.AB>2CD
C.AB<2CD D.无法确定
13.如图8,AB是☉O的直径,C,D为半圆的三等分点,CE⊥AB于点E,则∠ACE的度数为 .
8
14.如图9,A,B是半径为3的☉O上的两点,若∠AOB=120°,C是的中点,则四边形AOBC的周长等于 .
9
15.如图0,已知半圆的直径AB为3,圆心为O,弦AC与弦BD相交于点E,OD⊥AC,垂足为F,AC=BD,则弦AC的长为 .
0
16.如图1所示,以 ABCD的顶点A为圆心,AB的长为半径作圆,分别交AD,BC于点E,F,延长BA交☉A于点G.
(1)求证:=;
(2)若∠D=50°,求的度数.
1
17.如图2,在☉O中,弦AD,BC相交于点E,连接OE,AB,CD.已知AD=BC,AD⊥BC.
(1)求证:AB=CD;
(2)如图果☉O的直径为10,DE=1,求AE的长.
2
18.如图3①,PC是☉O的直径,PA与PB是弦,且∠APC=∠BPC.
(1)求证:PA=PB;
(2)如图图②,如图果点P由圆上运动到圆外,且PC过圆心,是否仍有PA=PB 为什么
(3)如图图③,如图果点P由圆上运动到圆内,PA=PB还成立吗 (无需证明)
3
答案
1.D 根据圆心角的概念,圆心角的顶点必须为圆心,即可判定选项D正确.
2.60°
3.(1)CD OF (2) ∠AOD OF
4.D 在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对弦的弦心距相等.题干中没有“同圆或等圆”的条件.
5.A 6.D 7.A
8. 60 等边
9.48° ∵==,∠COD=32°,
∴∠BOC=∠EOD=∠COD=32°,
∴∠AOE=180°-∠EOD-∠COD-∠BOC=84°.
又∵OA=OE,∴∠AEO=∠OAE,
∴∠AEO=×(180°-84°)=48°.
10.解:连接OE.
∵的度数为40°,∴∠COE=40°.
∵OC=OE,
∴∠OEC=×(180°-40°)=70°.
∵CE∥AB,
∴∠AOE=∠OEC=70°,
∴的度数为70°.
11.证明:连接OM,ON,如图图.
∵M,N分别为AB,CD的中点,
∴OM⊥AB,ON⊥CD,
∴∠AMO=∠CNO=90°.
∵AB=CD,
∴OM=ON,
∴∠OMN=∠ONM,
∴∠AMN=∠CNM.
12.C 利用圆的旋转对称性,使点C与点A重合,则D为的中点,这样有CD=BD.在△ABD中,利用三角形三边之间的关系有AB
∵在☉O中,==,
∴∠AOC=∠COD=∠DOB=60°.
∵OA=OC,
∴△AOC是等边三角形,
∴∠A=60°.
∵CE⊥OA,∴∠AEC=90°,
∴∠ACE=90°-60°=30°.
14.12 ∵C是的中点,∴=,
∴∠AOC=∠BOC,而∠AOB=120°,∴∠AOC=∠BOC=60°,∴△AOC和△BOC都是等边三角形,
即OA=OB=CA=CB=3,
∴四边形AOBC的周长等于12.
15. 如图图,连接OC.
∵OD⊥AC,
∴=,∠AFO=90°.
又∵AC=BD,
∴=,
即+=+,
∴=,
∴==,
∴∠AOD=∠DOC=∠BOC=60°.
∵AB=3,
∴AO=BO=,
∴AF=AOsin∠AOF=×=,
则AC=2AF=.
16.解:(1)证明:如图图,连接AF.
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EAF=∠AFB,∠GAE=∠B.
∵AB=AF,∴∠B=∠AFB,
∴∠EAF=∠GAE,∴=.
(2)∵四边形ABCD是平行四边形,
∴∠B=∠D=50°,∴∠GAE=∠EAF=50°,
则∠GAF=100°,
∴的度数为100°.
17.解:(1)证明:∵AD=BC,∴=,
∴-=-,即=,
∴AB=CD.
(2)如图图,过点O作OF⊥AD于点F,OG⊥BC于点G,连接OA.
∵AD=BC,
∴OF=OG.
又∵AD⊥BC,
∴四边形OFEG是正方形,
∴OF=EF.
设OF=EF=x,则AF=FD=x+1.
在Rt△OAF中,由勾股定理,得
x2+(x+1)2=52,解得x=3.
则AF=3+1=4,
∴AE=AF+EF=7.
18.解:(1)证明:过点O作OE⊥PA于点E,
OF⊥PB于点F,则有∠PEO=∠PFO=90°.
又∵∠APC=∠BPC,OP=OP,
∴△POE≌△POF,
∴OE=OF,∴PA=PB.
(2)仍有PA=PB.理由如图下:
过点O作OE⊥PA于点E,OF⊥PB于点F,同(1)可证△POE≌△POF,
∴PE=PF,OE=OF.
连接OA,OB,在Rt△AOE与Rt△BOF中,
AE=,BF=.
∵OA=OB,OE=OF,∴AE=BF,
∴PE+AE=PF+BF,即PA=PB.
(3)成立.
