沪科版数学九年级下册同步课时练习:24.3 第1课时 圆周角定理及其推论(word版含答案)
文档属性
| 名称 | 沪科版数学九年级下册同步课时练习:24.3 第1课时 圆周角定理及其推论(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 260.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 00:00:00 | ||
图片预览





文档简介
24.3 第1课时 圆周角定理及其推论
知识点 1 圆周角的定义
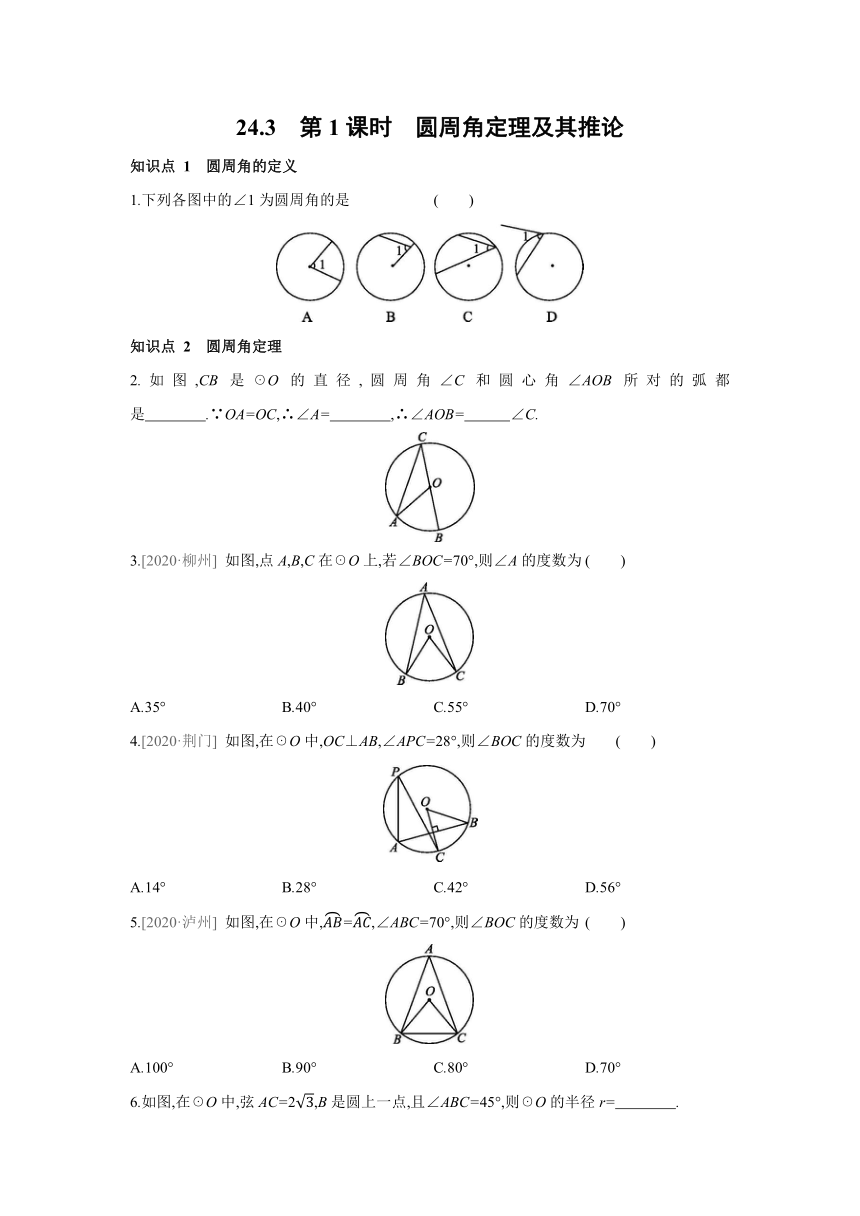
1.下列各图中的∠1为圆周角的是 ( )
知识点 2 圆周角定理
2.如图,CB是☉O的直径,圆周角∠C和圆心角∠AOB所对的弧都是 .∵OA=OC,∴∠A= ,∴∠AOB= ∠C.
3.[2020·柳州] 如图,点A,B,C在☉O上,若∠BOC=70°,则∠A的度数为 ( )
A.35° B.40° C.55° D.70°
4.[2020·荆门] 如图,在☉O中,OC⊥AB,∠APC=28°,则∠BOC的度数为 ( )
A.14° B.28° C.42° D.56°
5.[2020·泸州] 如图,在☉O中,=,∠ABC=70°,则∠BOC的度数为 ( )
A.100° B.90° C.80° D.70°
6.如图,在☉O中,弦AC=2,B是圆上一点,且∠ABC=45°,则☉O的半径r= .
7.[2020·淮南月考] 如图,AB为☉O的直径,∠BED=40°,则∠ACD= °.
知识点 3 圆周角定理的推论
8.用三角尺检查半圆形的工件,下列哪个工件是合格的 ( )
9.[教材练习第2题变式] 如图,在☉O中,∠AOB=80°,C,D是☉O上的任意两点,则∠C+∠D等于 ( )
A.80° B.90°
C.100° D.110°
10.[2020·阜新] 如图0,AB为☉O的直径,C,D是☉O上的两点,若∠ABC=38°,则∠BDC的度数为 ( )
0
A.57° B.52° C.38° D.26°
11.如图1,C,D两点在以AB为直径的☉O上,AB=2,∠ACD=30°,则AD= .
1
12.如图2,AB是☉O的直径,弦CD⊥AB于点E,连接AC,BC.
(1)求证:∠A=∠BCD;
(2)若AB=10,CD=6,求BE的长.
2
13.如图3所示,阴影部分为暗礁区,两灯塔A,B之间的距离恰好等于圆半径的倍,为了使航船(C)不进入暗礁区,那么C对两灯塔A,B的视角∠ACB必须 ( )
3
A.大于60° B.小于60°
C.大于45° D.小于45°
14.[2020·陕西] 如图4,点A,B,C在☉O上,BC∥OA,连接BO并延长交☉O于点D,连接AC,DC.若∠A=25°,则∠D的大小为 ( )
4
A.25° B.30° C.40° D.50°
15.如图5,BC为半圆的直径,A是半圆上一点,∠B=30°,将沿AB折叠,交BC于点D,CD=2,则BC的长为 ( )
5
A. B.4 C. D.5
16.如图6,△ABC内接于☉O,∠CAB=30°,∠CBA=45°,CD⊥AB于点D.若☉O的半径为2,则CD的长为 .
6
17.如图7,A,P,B,C是☉O上的四个点,∠APC=∠CPB=60°,试判断△ABC的形状,并证明你的结论.
7
18.如图8,AB是☉O的直径,AC,BC是☉O的弦,∠ACB的平分线交☉O于点D,连接AD,BD.已知AB=6,BC=2.
(1)求AC,AD,BD的长;
(2)求四边形ACBD的面积.
8
19.如图9,△ABC内接于☉O,已知AB=c,BC=a,AC=b,☉O的半径为R.
(1)求证:===2R;
(2)若a=5,∠A=60°,求☉O的半径R.
9
答案
1.C 根据圆周角的定义:顶点在圆上,并且两边都与圆还有另一个公共点的角叫做圆周角,即可求得答案.
2. ∠C 2
3.A ∵∠BOC=70°,
∴∠A=∠BOC=35°.
故选A.
4.D ∵在☉O中,OC⊥AB,∴=.
∵∠APC=28°,∴∠BOC=2∠APC=56°.
故选D.
5.C ∵=,
∴∠ABC=∠ACB=70°,
∴∠A=180°-70°-70°=40°,
∴∠BOC=2∠A=80°.
故选C.
6. ∵∠ABC=45°,
∴∠O=90°,
∴AC2=AO2+CO2,即(2)2=r2+r2,
解得r=.
7.50 如图图,连接OD.
∵∠BED=40°,
∴∠BOD=80°.
∵AB为☉O的直径,
∴∠AOB=180°
∴∠AOD=100°,
∴∠ACD=50°.
故答案为50.
8.C 根据90°的圆周角所对的弦是直径,可得只有C选项正确,其他均不正确.故选C.
9.A ∵∠AOB=80°,∴∠C=∠D=∠AOB=40°,∴∠C+∠D=80°.故选A.
10.B 如图图,连接AC.
∵AB是☉O的直径,∴∠ACB=90°.
∵∠ABC=38°,
∴∠BAC=90°-∠ABC=52°,
∴∠BDC=∠BAC=52°.
故选B.
11.1 ∵AB是☉O的直径,
∴∠ADB=90°.
又∵∠B=∠ACD=30°,∴AD=AB=1.
12.解:(1)证明:∵AB⊥CD,
∴=,∴∠A=∠BCD.
(2)连接OC.
∵AB⊥CD,CD=6,∴CE=ED=3.
∵直径AB=10,∴CO=OB=5.
在Rt△COE中,∵OC=5,CE=3,
∴OE==4,
∴BE=OB-OE=5-4=1.
13.D 设圆心为O,连接OA,OB,AB,BD,如图图所示.
∵AO=BO,AB=AO,
∴△AOB为直角三角形,∴∠AOB=90°.
∵∠ADB与∠AOB所对的弧都为,
∴∠ADB=∠AOB=45°.
∵∠ADB为△DCB的外角,
∴∠ADB>∠ACB,即∠ACB<45°.
故选D.
14.C ∵BC∥OA,
∴∠ACB=∠A=25°,∠B=∠AOB.
∵∠AOB=2∠ACB,
∴∠B=∠AOB=50°.
∵BD是☉O的直径,∴∠BCD=90°,
∴∠D=90°-∠B=90°-50°=40°.
故选C.
15.B 如图图,连接AD,作点D关于AB的对称点M,连接DM,BM.
由折叠可知,=,
∠ABC=∠MBA=30°,
∴==,
∴AC=AD.
∵BC是半圆的直径,
∴∠CAB=90°,
又∵∠B=30°,∴∠C=60°,
∴△ACD是等边三角形,
∴AC=CD=2,
∴BC=2AC=4.
故选B.
16. 如图图,连接CO并延长交☉O于点E,连接BE,则∠E=∠A=30°,∠EBC=90°.
∵☉O的半径为2,∴CE=4,
∴BC=CE=2.
∵CD⊥AB,∠CBA=45°,∴CD=BC=.
故答案为.
17.解:△ABC是等边三角形.
证明:在☉O中,
∵∠BAC与∠CPB是所对的圆周角,∠ABC与∠APC是所对的圆周角,
∴∠BAC=∠CPB=60°,∠ABC=∠APC=60°,
∴△ABC为等边三角形.
18.解:(1)∵AB是☉O的直径,
∴∠ACB=∠ADB=90°.
在Rt△ACB中,由勾股定理,得AC==4.
∵∠ACB的平分线交☉O于点D,
∴∠ACD=∠BCD=45°,
∴=,∴AD=BD.
在Rt△ADB中,AD=BD=AB=3.
(2)四边形ACBD的面积为AD·BD+BC·AC=9+4.
19.解:(1)证明:如图图,作直径BD,连接CD.
∵BD是☉O的直径,∴∠BCD=90°,
∴sinD=.
∵∠D=∠BAC,BC=a,BD=2R,
∴sin∠BAC=,即=2R.
同理,作直径CE,连接AE,
可得=2R.
作直径AF,连接BF,可得=2R.
∴===2R.
(2)由(1),知=2R.
当a=5,∠A=60°时,2R=,
∴R=.
知识点 1 圆周角的定义
1.下列各图中的∠1为圆周角的是 ( )
知识点 2 圆周角定理
2.如图,CB是☉O的直径,圆周角∠C和圆心角∠AOB所对的弧都是 .∵OA=OC,∴∠A= ,∴∠AOB= ∠C.
3.[2020·柳州] 如图,点A,B,C在☉O上,若∠BOC=70°,则∠A的度数为 ( )
A.35° B.40° C.55° D.70°
4.[2020·荆门] 如图,在☉O中,OC⊥AB,∠APC=28°,则∠BOC的度数为 ( )
A.14° B.28° C.42° D.56°
5.[2020·泸州] 如图,在☉O中,=,∠ABC=70°,则∠BOC的度数为 ( )
A.100° B.90° C.80° D.70°
6.如图,在☉O中,弦AC=2,B是圆上一点,且∠ABC=45°,则☉O的半径r= .
7.[2020·淮南月考] 如图,AB为☉O的直径,∠BED=40°,则∠ACD= °.
知识点 3 圆周角定理的推论
8.用三角尺检查半圆形的工件,下列哪个工件是合格的 ( )
9.[教材练习第2题变式] 如图,在☉O中,∠AOB=80°,C,D是☉O上的任意两点,则∠C+∠D等于 ( )
A.80° B.90°
C.100° D.110°
10.[2020·阜新] 如图0,AB为☉O的直径,C,D是☉O上的两点,若∠ABC=38°,则∠BDC的度数为 ( )
0
A.57° B.52° C.38° D.26°
11.如图1,C,D两点在以AB为直径的☉O上,AB=2,∠ACD=30°,则AD= .
1
12.如图2,AB是☉O的直径,弦CD⊥AB于点E,连接AC,BC.
(1)求证:∠A=∠BCD;
(2)若AB=10,CD=6,求BE的长.
2
13.如图3所示,阴影部分为暗礁区,两灯塔A,B之间的距离恰好等于圆半径的倍,为了使航船(C)不进入暗礁区,那么C对两灯塔A,B的视角∠ACB必须 ( )
3
A.大于60° B.小于60°
C.大于45° D.小于45°
14.[2020·陕西] 如图4,点A,B,C在☉O上,BC∥OA,连接BO并延长交☉O于点D,连接AC,DC.若∠A=25°,则∠D的大小为 ( )
4
A.25° B.30° C.40° D.50°
15.如图5,BC为半圆的直径,A是半圆上一点,∠B=30°,将沿AB折叠,交BC于点D,CD=2,则BC的长为 ( )
5
A. B.4 C. D.5
16.如图6,△ABC内接于☉O,∠CAB=30°,∠CBA=45°,CD⊥AB于点D.若☉O的半径为2,则CD的长为 .
6
17.如图7,A,P,B,C是☉O上的四个点,∠APC=∠CPB=60°,试判断△ABC的形状,并证明你的结论.
7
18.如图8,AB是☉O的直径,AC,BC是☉O的弦,∠ACB的平分线交☉O于点D,连接AD,BD.已知AB=6,BC=2.
(1)求AC,AD,BD的长;
(2)求四边形ACBD的面积.
8
19.如图9,△ABC内接于☉O,已知AB=c,BC=a,AC=b,☉O的半径为R.
(1)求证:===2R;
(2)若a=5,∠A=60°,求☉O的半径R.
9
答案
1.C 根据圆周角的定义:顶点在圆上,并且两边都与圆还有另一个公共点的角叫做圆周角,即可求得答案.
2. ∠C 2
3.A ∵∠BOC=70°,
∴∠A=∠BOC=35°.
故选A.
4.D ∵在☉O中,OC⊥AB,∴=.
∵∠APC=28°,∴∠BOC=2∠APC=56°.
故选D.
5.C ∵=,
∴∠ABC=∠ACB=70°,
∴∠A=180°-70°-70°=40°,
∴∠BOC=2∠A=80°.
故选C.
6. ∵∠ABC=45°,
∴∠O=90°,
∴AC2=AO2+CO2,即(2)2=r2+r2,
解得r=.
7.50 如图图,连接OD.
∵∠BED=40°,
∴∠BOD=80°.
∵AB为☉O的直径,
∴∠AOB=180°
∴∠AOD=100°,
∴∠ACD=50°.
故答案为50.
8.C 根据90°的圆周角所对的弦是直径,可得只有C选项正确,其他均不正确.故选C.
9.A ∵∠AOB=80°,∴∠C=∠D=∠AOB=40°,∴∠C+∠D=80°.故选A.
10.B 如图图,连接AC.
∵AB是☉O的直径,∴∠ACB=90°.
∵∠ABC=38°,
∴∠BAC=90°-∠ABC=52°,
∴∠BDC=∠BAC=52°.
故选B.
11.1 ∵AB是☉O的直径,
∴∠ADB=90°.
又∵∠B=∠ACD=30°,∴AD=AB=1.
12.解:(1)证明:∵AB⊥CD,
∴=,∴∠A=∠BCD.
(2)连接OC.
∵AB⊥CD,CD=6,∴CE=ED=3.
∵直径AB=10,∴CO=OB=5.
在Rt△COE中,∵OC=5,CE=3,
∴OE==4,
∴BE=OB-OE=5-4=1.
13.D 设圆心为O,连接OA,OB,AB,BD,如图图所示.
∵AO=BO,AB=AO,
∴△AOB为直角三角形,∴∠AOB=90°.
∵∠ADB与∠AOB所对的弧都为,
∴∠ADB=∠AOB=45°.
∵∠ADB为△DCB的外角,
∴∠ADB>∠ACB,即∠ACB<45°.
故选D.
14.C ∵BC∥OA,
∴∠ACB=∠A=25°,∠B=∠AOB.
∵∠AOB=2∠ACB,
∴∠B=∠AOB=50°.
∵BD是☉O的直径,∴∠BCD=90°,
∴∠D=90°-∠B=90°-50°=40°.
故选C.
15.B 如图图,连接AD,作点D关于AB的对称点M,连接DM,BM.
由折叠可知,=,
∠ABC=∠MBA=30°,
∴==,
∴AC=AD.
∵BC是半圆的直径,
∴∠CAB=90°,
又∵∠B=30°,∴∠C=60°,
∴△ACD是等边三角形,
∴AC=CD=2,
∴BC=2AC=4.
故选B.
16. 如图图,连接CO并延长交☉O于点E,连接BE,则∠E=∠A=30°,∠EBC=90°.
∵☉O的半径为2,∴CE=4,
∴BC=CE=2.
∵CD⊥AB,∠CBA=45°,∴CD=BC=.
故答案为.
17.解:△ABC是等边三角形.
证明:在☉O中,
∵∠BAC与∠CPB是所对的圆周角,∠ABC与∠APC是所对的圆周角,
∴∠BAC=∠CPB=60°,∠ABC=∠APC=60°,
∴△ABC为等边三角形.
18.解:(1)∵AB是☉O的直径,
∴∠ACB=∠ADB=90°.
在Rt△ACB中,由勾股定理,得AC==4.
∵∠ACB的平分线交☉O于点D,
∴∠ACD=∠BCD=45°,
∴=,∴AD=BD.
在Rt△ADB中,AD=BD=AB=3.
(2)四边形ACBD的面积为AD·BD+BC·AC=9+4.
19.解:(1)证明:如图图,作直径BD,连接CD.
∵BD是☉O的直径,∴∠BCD=90°,
∴sinD=.
∵∠D=∠BAC,BC=a,BD=2R,
∴sin∠BAC=,即=2R.
同理,作直径CE,连接AE,
可得=2R.
作直径AF,连接BF,可得=2R.
∴===2R.
(2)由(1),知=2R.
当a=5,∠A=60°时,2R=,
∴R=.
