沪科版数学九年级下册同步课时练习:24.4 第2课时 切线的判定(word版含答案)
文档属性
| 名称 | 沪科版数学九年级下册同步课时练习:24.4 第2课时 切线的判定(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 186.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 19:10:35 | ||
图片预览



文档简介
第2课时 切线的判定
知识点 1 利用切线的定义判定切线
1.已知☉O的半径为3,点A在☉O上,直线l经过点A,P是直线l上任意一点,且OP≥3,则点P与☉O的位置关系是 ,直线l与☉O的公共点的个数为 ,故直线l与☉O的位置关系是 .
2.在Rt△ABC中,∠C=90°,AB=10 cm,BC=8 cm,若以点A为圆心,6 cm为半径作☉A,则直线BC与☉A的位置关系是 ( )
A.相交 B.相切
C.相离 D.相交或相切
知识点 2 切线的判定——有公共点,连半径,证垂直
3.如图7,A是☉O上一点,且AO=5,PO=13,AP=12,则PA与☉O的位置关系是 ( )
A.相离 B.相切
C.相交 D.相切或相交
7 8
4.如图8,△ABC的一边AB是☉O的直径,请你添加一个条件,使BC是☉O的切线,你所添加的条件为 .
5.如图9所示,AB是☉O的直径,C为☉O上一点,过点B作BD⊥CD,垂足为D,连接BC,BC平分∠ABD.
求证:CD为☉O的切线.
9
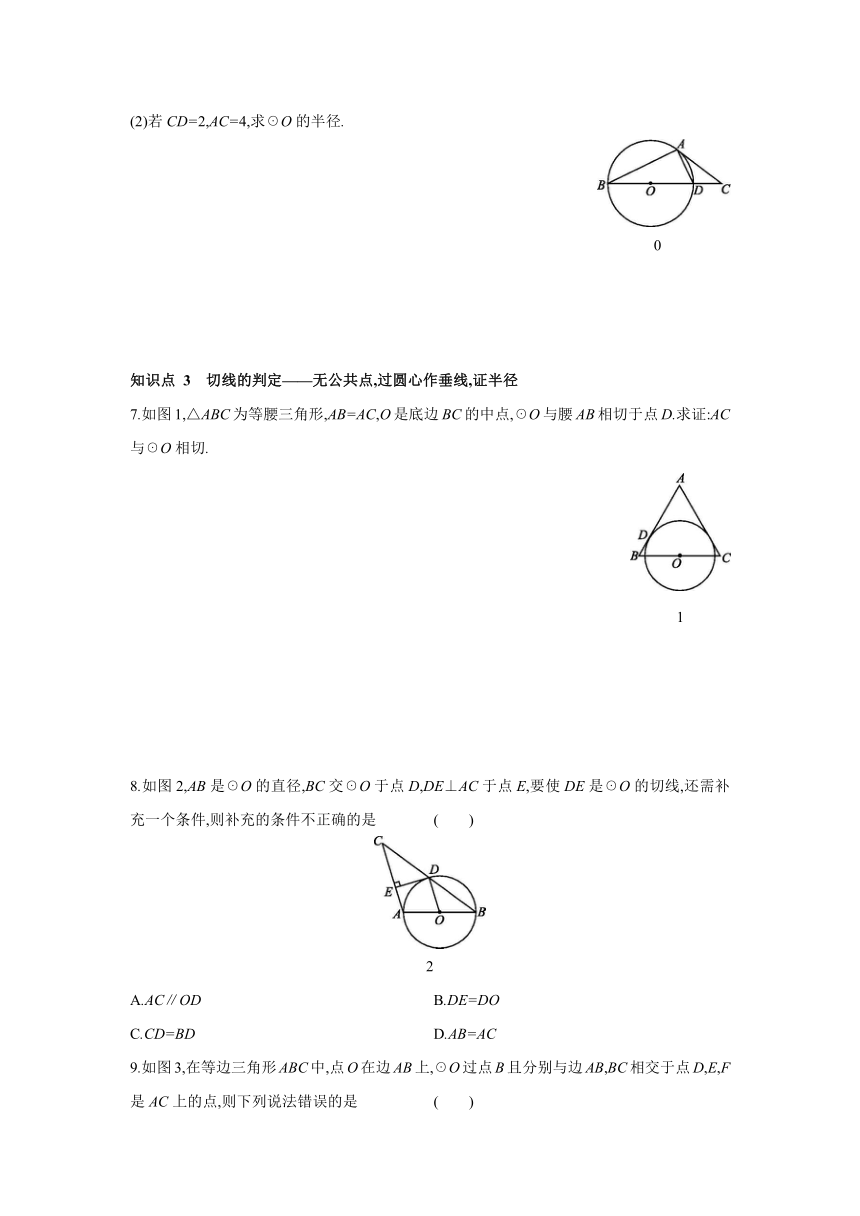
6.[2020·宿迁改编] 如图0,在△ABC中,D是边BC上一点,以BD为直径的☉O经过点A,且∠CAD=∠ABC.
(1)请判断直线AC是不是☉O的切线,并说明理由;
(2)若CD=2,AC=4,求☉O的半径.
0
知识点 3 切线的判定——无公共点,过圆心作垂线,证半径
7.如图1,△ABC为等腰三角形,AB=AC,O是底边BC的中点,☉O与腰AB相切于点D.求证:AC与☉O相切.
1
8.如图2,AB是☉O的直径,BC交☉O于点D,DE⊥AC于点E,要使DE是☉O的切线,还需补充一个条件,则补充的条件不正确的是 ( )
2
A.AC∥OD B.DE=DO
C.CD=BD D.AB=AC
9.如图3,在等边三角形ABC中,点O在边AB上,☉O过点B且分别与边AB,BC相交于点D,E,F是AC上的点,则下列说法错误的是 ( )
3
A.若EF⊥AC,则EF是☉O的切线
B.若EF是☉O的切线,则EF⊥AC
C.若BE=EC,则AC是☉O的切线
D.若BE=EC,则AC是☉O的切线
10.如图4,在平面直角坐标系中,以点C(2,0)为圆心,3为半径的圆交x轴正半轴于点A,交y轴正半轴于点B,过点B的直线交x轴负半轴于点D-,0.
(1)求A,B两点的坐标;
(2)求证:直线BD是☉C的切线.
4
11.[2020·马鞍山二模] 如图5,已知AB为☉O的弦,C为☉O上一点,∠C=∠BAD,且BD⊥AB于点B.
(1)求证:AD是☉O的切线;
(2)若☉O的半径为3,AB=4,求AD的长.
5
12.如图6,在△ABC中,∠A=90°,∠B=60°,AB=3,点D从点A开始以每秒1个单位的速度向点B运动(点D不与点B重合),过点D作DE∥BC交AC于点E.以DE为直径作☉O,并在☉O内作其内接矩形ADFE.设点D的运动时间为t秒.
6
(1)当0(2)当t= 时,☉O与直线BC相切.
答案
1.点P在☉O上或在☉O外 1 相切
2.B
3.B ∵AO=5,PO=13,AP=12,
∴AO2+AP2=PO2,∴∠PAO=90°,
∴PA⊥OA.
又∵A是☉O上一点,∴PA与☉O相切.
故选B.
4.答案不唯一,如图BC⊥AB 根据切线的判定来判断,当BC⊥AB时,BC是☉O的切线.
5.证明:∵BC平分∠ABD,∴∠OBC=∠DBC.
∵OB=OC,∴∠OBC=∠OCB,
∴∠OCB=∠DBC,
∴OC∥BD.
∵BD⊥CD,∴OC⊥CD.
又∵OC为☉O的半径,
∴CD为☉O的切线.
6.解:(1)直线AC是☉O的切线.理由如图下:
如图图,连接OA.
∵BD为☉O的直径,
∴∠BAD=90°.
∵OA=OB,
∴∠OAB=∠ABC.
又∵∠CAD=∠ABC,
∴∠CAD=∠OAB,
∴∠OAC=∠OAD+∠CAD=∠OAD+∠OAB=∠BAD=90°,
∴AC⊥OA.
又∵点A在☉O上,
∴直线AC是☉O的切线.
(2)∵∠CAD=∠ABC,∠C=∠C,
∴△CAD∽△CBA,∴=.
∵CD=2,AC=4,
∴=,∴BC=8,
∴BD=BC-CD=8-2=6,
∴☉O的半径为3.
7.证明:连接AO,OD,过点O作OE⊥AC于点E.
∵AB与☉O相切,∴OD⊥AB.
∵AB=AC,O是底边BC的中点,
∴∠BAO=∠CAO,
∴OE=OD,即点O到AC的距离等于半径,
∴AC与☉O相切.
8.B 当AC∥OD时,∵DE⊥AC,∴DE⊥OD,∴DE是☉O的切线.故A项正确;当CD=BD时,AO=BO,∴OD是△ABC的中位线,∴OD∥AC.∵DE⊥AC,∴DE⊥OD,∴DE是☉O的切线.故C项正确;当AB=AC时,连接AD.∵AB是☉O的直径,∴AD⊥BC,∴CD=BD.∵AO=BO,∴OD是△ABC的中位线,∴OD∥AC.∵DE⊥AC,∴DE⊥OD,∴DE是☉O的切线.故D项正确;根据排除法,故选B.
9.C A项,如图图①,连接OE,则OB=OE.∵∠B=60°,∴∠BOE=60°.
∵∠BAC=60°,∴∠BOE=∠BAC,
∴OE∥AC.
∵EF⊥AC,∴OE⊥EF,∴EF是☉O的切线,∴A选项正确,不符合题意;
B项,∵EF是☉O的切线,∴OE⊥EF,由A项知OE∥AC,∴AC⊥EF,∴B选项正确,不符合题意;
C项,∵∠B=60°,OB=OE,∴BE=OB.
∵BE=EC,∴BC=AB=2BO,∴AO=OB.
如图图②,过点O作OH⊥AC于点H.
∵∠BAC=60°,∴OH=AO≠OB,
∴C选项错误,符合题意;
D项,如图图②,∵BE=EC,∴EC=BE.
∵AB=BC,BO=BE,∴AO=EC=OB,
∴OH=AO=OB,
∴AC是☉O的切线,
∴D选项正确,不符合题意.
故选C.
10.解:(1)∵点C(2,0),圆的半径为3,
∴OC=2,AC=3,
∴OA=OC+AC=5,∴A(5,0).
如图图,连接CB.在Rt△OCB中,
∵OB===,
∴B(0,).
(2)证明:∵点D-,0,∴OD=.
在Rt△DBO中,
BD2=OB2+OD2=5+=.
∵DC=DO+OC=,CB=3,
∴在△DBC中,
BD2+CB2=+9==DC2,
∴△DBC是直角三角形,
∴CB⊥BD.
∵CB是☉C的半径,
∴直线BD是☉C的切线.
11.解:(1)证明:如图图,连接AO并延长交☉O于点E,连接BE,则∠ABE=90°,
∴∠EAB+∠E=90°.
∵∠E=∠C,∠C=∠BAD,
∴∠BAD=∠E,
∴∠EAB+∠BAD=90°.
又∵点A在☉O上,∴AD是☉O的切线.
(2)由(1)可知∠BAD=∠E,∠ABE=90°.
∵AE=2AO=6,AB=4,
∴BE===2.
∵∠E=∠BAD,BD⊥AB,
∴cos∠BAD=cosE.
∴=,即=.
∴AD=.
12.(1)t2 (2)6-9
(1)∵DE∥BC,
∴∠ADE=∠B=60°.
在△ADE中,∵∠A=90°,
∴tan∠ADE=.
∵AD=1×t=t,∴AE=t.
∵四边形ADFE是矩形,
∴S△DEF=S△ADE=AD·AE=·t·t=t2(0(2)如图图,过点O作OG⊥BC于点G,过点D作DH⊥BC于点H,∴∠DHB=90°.
∵DE∥BC,∴OG=DH.
在Rt△DBH中,sinB=.
∵∠B=60°,BD=AB-AD,AD=t,AB=3,
∴DH=(3-t),∴OG=(3-t).
当OG=DE时,☉O与直线BC相切.
在Rt△ADE中,∵∠A=90°,∠ADE=60°,
∴cos∠ADE==.
∵AD=t,∴DE=2AD=2t,
∴2t=(3-t)×2,解得t=6-9.
∴当t=6-9时,☉O与直线BC相切.
知识点 1 利用切线的定义判定切线
1.已知☉O的半径为3,点A在☉O上,直线l经过点A,P是直线l上任意一点,且OP≥3,则点P与☉O的位置关系是 ,直线l与☉O的公共点的个数为 ,故直线l与☉O的位置关系是 .
2.在Rt△ABC中,∠C=90°,AB=10 cm,BC=8 cm,若以点A为圆心,6 cm为半径作☉A,则直线BC与☉A的位置关系是 ( )
A.相交 B.相切
C.相离 D.相交或相切
知识点 2 切线的判定——有公共点,连半径,证垂直
3.如图7,A是☉O上一点,且AO=5,PO=13,AP=12,则PA与☉O的位置关系是 ( )
A.相离 B.相切
C.相交 D.相切或相交
7 8
4.如图8,△ABC的一边AB是☉O的直径,请你添加一个条件,使BC是☉O的切线,你所添加的条件为 .
5.如图9所示,AB是☉O的直径,C为☉O上一点,过点B作BD⊥CD,垂足为D,连接BC,BC平分∠ABD.
求证:CD为☉O的切线.
9
6.[2020·宿迁改编] 如图0,在△ABC中,D是边BC上一点,以BD为直径的☉O经过点A,且∠CAD=∠ABC.
(1)请判断直线AC是不是☉O的切线,并说明理由;
(2)若CD=2,AC=4,求☉O的半径.
0
知识点 3 切线的判定——无公共点,过圆心作垂线,证半径
7.如图1,△ABC为等腰三角形,AB=AC,O是底边BC的中点,☉O与腰AB相切于点D.求证:AC与☉O相切.
1
8.如图2,AB是☉O的直径,BC交☉O于点D,DE⊥AC于点E,要使DE是☉O的切线,还需补充一个条件,则补充的条件不正确的是 ( )
2
A.AC∥OD B.DE=DO
C.CD=BD D.AB=AC
9.如图3,在等边三角形ABC中,点O在边AB上,☉O过点B且分别与边AB,BC相交于点D,E,F是AC上的点,则下列说法错误的是 ( )
3
A.若EF⊥AC,则EF是☉O的切线
B.若EF是☉O的切线,则EF⊥AC
C.若BE=EC,则AC是☉O的切线
D.若BE=EC,则AC是☉O的切线
10.如图4,在平面直角坐标系中,以点C(2,0)为圆心,3为半径的圆交x轴正半轴于点A,交y轴正半轴于点B,过点B的直线交x轴负半轴于点D-,0.
(1)求A,B两点的坐标;
(2)求证:直线BD是☉C的切线.
4
11.[2020·马鞍山二模] 如图5,已知AB为☉O的弦,C为☉O上一点,∠C=∠BAD,且BD⊥AB于点B.
(1)求证:AD是☉O的切线;
(2)若☉O的半径为3,AB=4,求AD的长.
5
12.如图6,在△ABC中,∠A=90°,∠B=60°,AB=3,点D从点A开始以每秒1个单位的速度向点B运动(点D不与点B重合),过点D作DE∥BC交AC于点E.以DE为直径作☉O,并在☉O内作其内接矩形ADFE.设点D的运动时间为t秒.
6
(1)当0
答案
1.点P在☉O上或在☉O外 1 相切
2.B
3.B ∵AO=5,PO=13,AP=12,
∴AO2+AP2=PO2,∴∠PAO=90°,
∴PA⊥OA.
又∵A是☉O上一点,∴PA与☉O相切.
故选B.
4.答案不唯一,如图BC⊥AB 根据切线的判定来判断,当BC⊥AB时,BC是☉O的切线.
5.证明:∵BC平分∠ABD,∴∠OBC=∠DBC.
∵OB=OC,∴∠OBC=∠OCB,
∴∠OCB=∠DBC,
∴OC∥BD.
∵BD⊥CD,∴OC⊥CD.
又∵OC为☉O的半径,
∴CD为☉O的切线.
6.解:(1)直线AC是☉O的切线.理由如图下:
如图图,连接OA.
∵BD为☉O的直径,
∴∠BAD=90°.
∵OA=OB,
∴∠OAB=∠ABC.
又∵∠CAD=∠ABC,
∴∠CAD=∠OAB,
∴∠OAC=∠OAD+∠CAD=∠OAD+∠OAB=∠BAD=90°,
∴AC⊥OA.
又∵点A在☉O上,
∴直线AC是☉O的切线.
(2)∵∠CAD=∠ABC,∠C=∠C,
∴△CAD∽△CBA,∴=.
∵CD=2,AC=4,
∴=,∴BC=8,
∴BD=BC-CD=8-2=6,
∴☉O的半径为3.
7.证明:连接AO,OD,过点O作OE⊥AC于点E.
∵AB与☉O相切,∴OD⊥AB.
∵AB=AC,O是底边BC的中点,
∴∠BAO=∠CAO,
∴OE=OD,即点O到AC的距离等于半径,
∴AC与☉O相切.
8.B 当AC∥OD时,∵DE⊥AC,∴DE⊥OD,∴DE是☉O的切线.故A项正确;当CD=BD时,AO=BO,∴OD是△ABC的中位线,∴OD∥AC.∵DE⊥AC,∴DE⊥OD,∴DE是☉O的切线.故C项正确;当AB=AC时,连接AD.∵AB是☉O的直径,∴AD⊥BC,∴CD=BD.∵AO=BO,∴OD是△ABC的中位线,∴OD∥AC.∵DE⊥AC,∴DE⊥OD,∴DE是☉O的切线.故D项正确;根据排除法,故选B.
9.C A项,如图图①,连接OE,则OB=OE.∵∠B=60°,∴∠BOE=60°.
∵∠BAC=60°,∴∠BOE=∠BAC,
∴OE∥AC.
∵EF⊥AC,∴OE⊥EF,∴EF是☉O的切线,∴A选项正确,不符合题意;
B项,∵EF是☉O的切线,∴OE⊥EF,由A项知OE∥AC,∴AC⊥EF,∴B选项正确,不符合题意;
C项,∵∠B=60°,OB=OE,∴BE=OB.
∵BE=EC,∴BC=AB=2BO,∴AO=OB.
如图图②,过点O作OH⊥AC于点H.
∵∠BAC=60°,∴OH=AO≠OB,
∴C选项错误,符合题意;
D项,如图图②,∵BE=EC,∴EC=BE.
∵AB=BC,BO=BE,∴AO=EC=OB,
∴OH=AO=OB,
∴AC是☉O的切线,
∴D选项正确,不符合题意.
故选C.
10.解:(1)∵点C(2,0),圆的半径为3,
∴OC=2,AC=3,
∴OA=OC+AC=5,∴A(5,0).
如图图,连接CB.在Rt△OCB中,
∵OB===,
∴B(0,).
(2)证明:∵点D-,0,∴OD=.
在Rt△DBO中,
BD2=OB2+OD2=5+=.
∵DC=DO+OC=,CB=3,
∴在△DBC中,
BD2+CB2=+9==DC2,
∴△DBC是直角三角形,
∴CB⊥BD.
∵CB是☉C的半径,
∴直线BD是☉C的切线.
11.解:(1)证明:如图图,连接AO并延长交☉O于点E,连接BE,则∠ABE=90°,
∴∠EAB+∠E=90°.
∵∠E=∠C,∠C=∠BAD,
∴∠BAD=∠E,
∴∠EAB+∠BAD=90°.
又∵点A在☉O上,∴AD是☉O的切线.
(2)由(1)可知∠BAD=∠E,∠ABE=90°.
∵AE=2AO=6,AB=4,
∴BE===2.
∵∠E=∠BAD,BD⊥AB,
∴cos∠BAD=cosE.
∴=,即=.
∴AD=.
12.(1)t2 (2)6-9
(1)∵DE∥BC,
∴∠ADE=∠B=60°.
在△ADE中,∵∠A=90°,
∴tan∠ADE=.
∵AD=1×t=t,∴AE=t.
∵四边形ADFE是矩形,
∴S△DEF=S△ADE=AD·AE=·t·t=t2(0
∵DE∥BC,∴OG=DH.
在Rt△DBH中,sinB=.
∵∠B=60°,BD=AB-AD,AD=t,AB=3,
∴DH=(3-t),∴OG=(3-t).
当OG=DE时,☉O与直线BC相切.
在Rt△ADE中,∵∠A=90°,∠ADE=60°,
∴cos∠ADE==.
∵AD=t,∴DE=2AD=2t,
∴2t=(3-t)×2,解得t=6-9.
∴当t=6-9时,☉O与直线BC相切.
