沪科版数学九年级下册同步课时练习:24.4 第3课时 切线长定理(word版含答案)
文档属性
| 名称 | 沪科版数学九年级下册同步课时练习:24.4 第3课时 切线长定理(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 237.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 00:00:00 | ||
图片预览

文档简介
第3课时 切线长定理
知识点 切线长与切线长定理
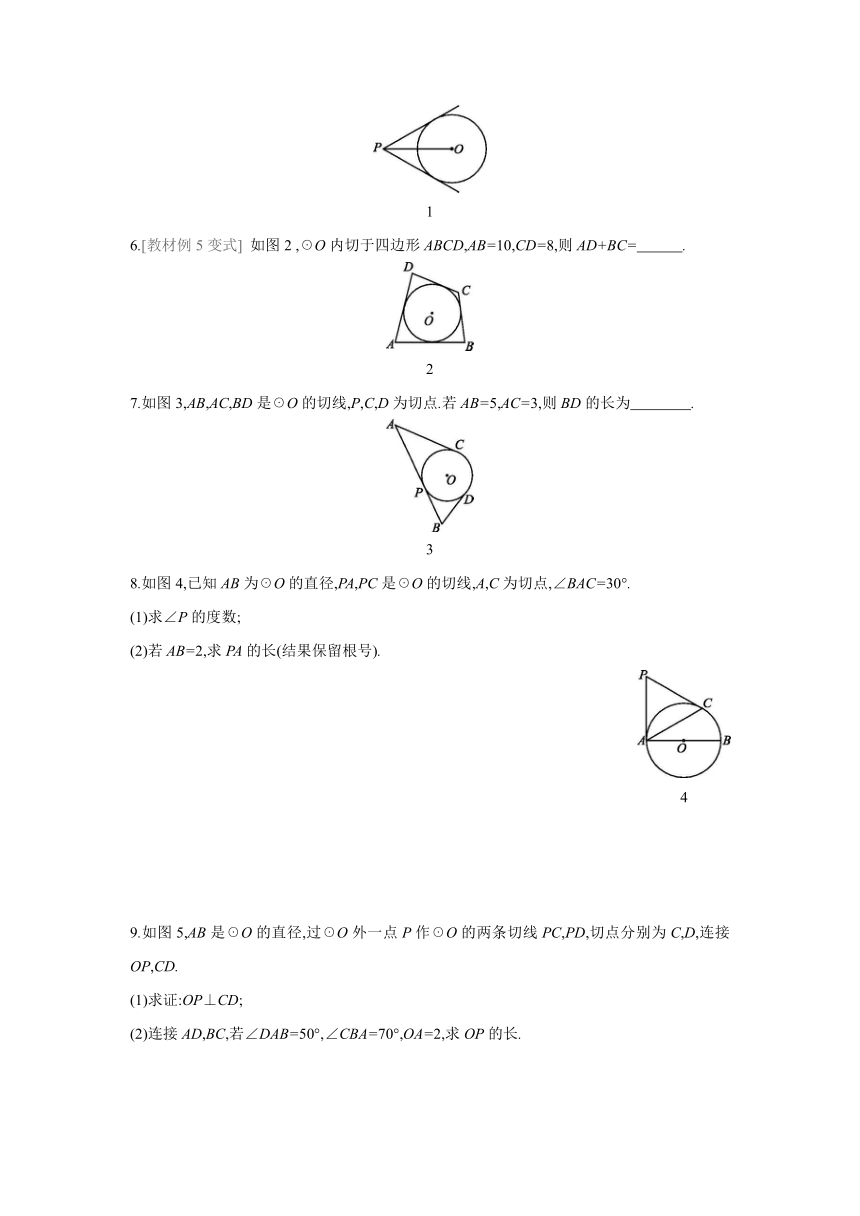
1.如图7,P为☉O外一点,PA,PB分别切☉O于A,B两点.若PA=3,则PB的长度为 ( )
7
A.2 B.3 C.4 D.5
2.如图8,PA切☉O于点A,PB切☉O于点B,连接OP.若∠APO=30°,OA=2,则PB的长为 ( )
8
A. B. C.4 D.2
3.如图9,PA切☉O于点A,PB切☉O于点B,OP交☉O于点C,则下列结论中错误的是( )
9
A.∠1=∠2 B.PA=PB
C.AB⊥OP D.∠PAB=2∠1
4.如图0,从☉O外一点P引☉O的两条切线PA,PB,切点分别为A,B.若∠APB=60°,弦
AB=4,则PA= .
0
5.如图1,☉O的半径为3 cm,点P到圆心O的距离为6 cm,过点P引☉O的两条切线,这两条切线的夹角为 度.
1
6.[教材例5变式] 如图2 ,☉O内切于四边形ABCD,AB=10,CD=8,则AD+BC= .
2
7.如图3,AB,AC,BD是☉O的切线,P,C,D为切点.若AB=5,AC=3,则BD的长为 .
3
8.如图4,已知AB为☉O的直径,PA,PC是☉O的切线,A,C为切点,∠BAC=30°.
(1)求∠P的度数;
(2)若AB=2,求PA的长(结果保留根号).
4
9.如图5,AB是☉O的直径,过☉O外一点P作☉O的两条切线PC,PD,切点分别为C,D,连接OP,CD.
(1)求证:OP⊥CD;
(2)连接AD,BC,若∠DAB=50°,∠CBA=70°,OA=2,求OP的长.
5
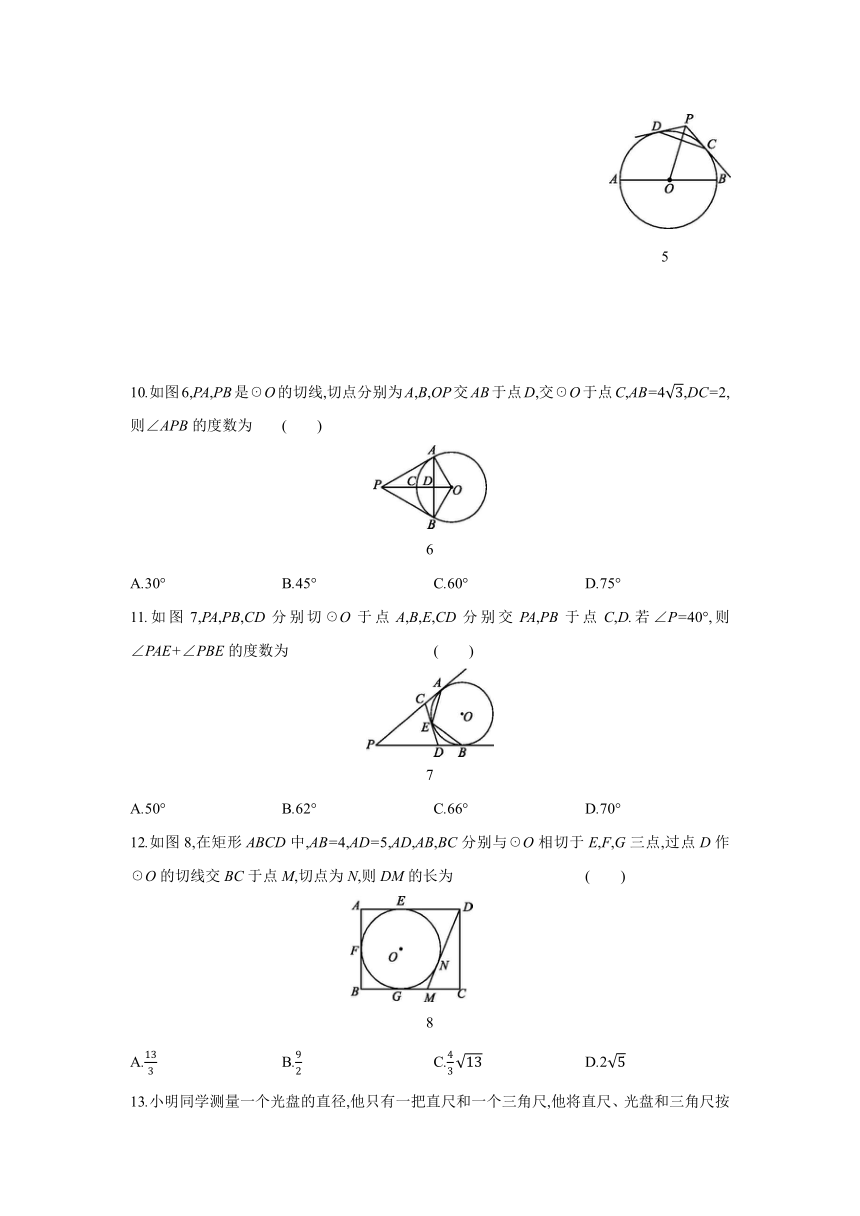
10.如图6,PA,PB是☉O的切线,切点分别为A,B,OP交AB于点D,交☉O于点C,AB=4,DC=2,则∠APB的度数为 ( )
6
A.30° B.45° C.60° D.75°
11.如图7,PA,PB,CD分别切☉O于点A,B,E,CD分别交PA,PB于点C,D.若∠P=40°,则∠PAE+∠PBE的度数为 ( )
7
A.50° B.62° C.66° D.70°
12.如图8,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与☉O相切于E,F,G三点,过点D作☉O的切线交BC于点M,切点为N,则DM的长为 ( )
8
A. B. C. D.2
13.小明同学测量一个光盘的直径,他只有一把直尺和一个三角尺,他将直尺、光盘和三角尺按9所示方式放置于桌面上,并量出AB=3 cm,则此光盘的直径是 cm.
9
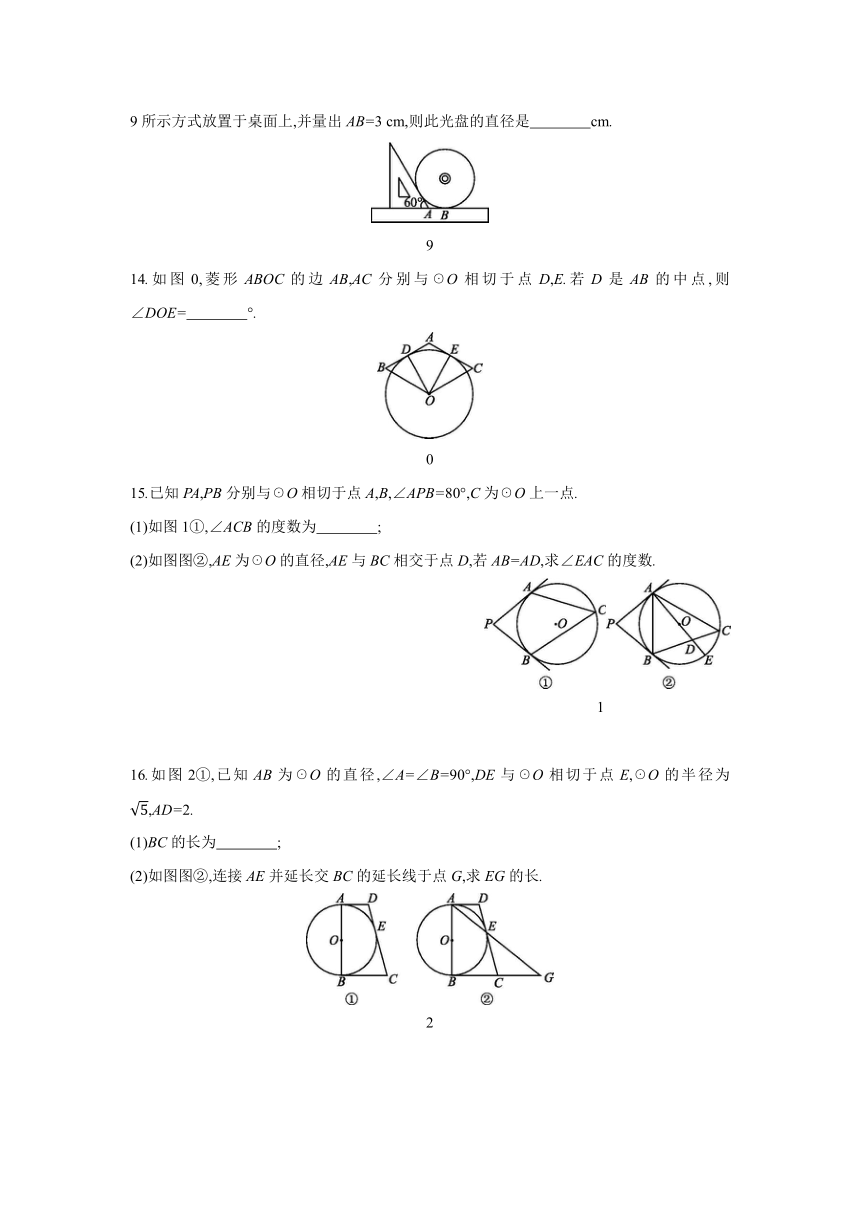
14.如图0,菱形ABOC的边AB,AC分别与☉O相切于点D,E.若D是AB的中点,则∠DOE= °.
0
15.已知PA,PB分别与☉O相切于点A,B,∠APB=80°,C为☉O上一点.
(1)如图1①,∠ACB的度数为 ;
(2)如图图②,AE为☉O的直径,AE与BC相交于点D,若AB=AD,求∠EAC的度数.
1
16.如图2①,已知AB为☉O的直径,∠A=∠B=90°,DE与☉O相切于点E,☉O的半径为,AD=2.
(1)BC的长为 ;
(2)如图图②,连接AE并延长交BC的延长线于点G,求EG的长.
2
答案
1.B
2.D ∵PA切☉O于点A,PB切☉O于点B,∴PA⊥OA,PB⊥OB,PA=PB.∵∠APO=30°,OA=2,∴OP=4,∴AP==2,∴BP=2.故选D.
3.D
4.4 ∵PA,PB是☉O的两条切线,∴PA=PB.又∵∠APB=60°,∴△PAB是等边三角形,∴PA=AB=4.
5.60
6.18 根据切线长定理,知AB+CD=AD+BC.
7.2 ∵AC,AP为☉O的切线,
∴AC=AP.
∵BP,BD为☉O的切线,∴BP=BD,
∴BD=BP=AB-AP=AB-AC=5-3=2.
故答案为2.
8.解:(1)∵PA是☉O的切线,AB为☉O的直径,
∴PA⊥AB,∴∠BAP=90°.
∵∠BAC=30°,∴∠CAP=90°-∠BAC=60°.
∵PA,PC分别切☉O于点A,C,∴PA=PC,
∴△PAC为等边三角形,∴∠P=60°.
(2)如图图,连接BC,则∠ACB=90°.
在Rt△ACB中,AB=2,∠BAC=30°,
∴AC=ABcos∠BAC=2cos30°=.
∵△PAC为等边三角形,∴PA=AC=.
9.解:(1)证明:如图图,连接OC,OD.
∵PD,PC是☉O的切线,∴PD=PC.
∵OD=OC,∴点P,O在CD的垂直平分线上,
∴OP⊥CD.
(2)如图图,连接AD,BC.
∵OA=OD=OC=OB=2,
∴∠ADO=∠DAO=50°,∠BCO=∠CBO=70°,
∴∠AOD=80°,∠BOC=40°,
∴∠COD=60°.
∵OD=OC,∴△COD是等边三角形.
∴∠DOP=∠COP=30°.
在Rt△ODP中,OP==.
10.C 连接AC,根据切线长定理,可得PA=PB,OP⊥AB,∴AD=AB=2,则tan∠ACD==,∴∠ACD=60°,∴△AOC是等边三角形,则∠AOP=60°,∴∠APO=30°,∴∠APB=60°.
11.D ∵PA,PB,CD分别切☉O于点A,B,E,CD分别交PA,PB于点C,D,
∴CE=CA,DE=DB,
∴∠CAE=∠CEA,∠DEB=∠DBE,
∴∠PCD=∠CAE+∠CEA=2∠CAE,∠PDC=∠DEB+∠DBE=2∠DBE,
∴∠CAE=∠PCD,∠DBE=∠PDC,
即∠PAE=∠PCD,∠PBE=∠PDC.
∵∠P=40°,
∴∠PAE+∠PBE=∠PCD+∠PDC=(∠PCD+∠PDC)=(180°-∠P)=70°.
故选D.
12.A 由题意可知AF=AE=BF=BG=2,DN=DE=3.设GM=x,则MN=x,DM=3+x,CM=3-x.在Rt△DMC中,∵DM2=CM2+CD2,即(3+x)2=(3-x)2+42,解得x=,∴DM=DN+MN=3+=.故选A.
13.6 如图图,连接OA,OB.
∵∠CAD=60°,
∴∠CAB=120°.
∵AB和AC与☉O相切,
∴∠OAB=∠OAC,
∴∠OAB=∠CAB=60°.
∵AB=3 cm,∴OA=6 cm.
在Rt△AOB中,由勾股定理,得OB=3 cm,
∴光盘的直径为6 cm.故答案为6.
14.60 如图图,连接OA.
∵四边形ABOC是菱形,
∴BA=BO.
∵AB与☉O相切于点D,
∴OD⊥AB.
∵D是AB的中点,
∴直线OD是线段AB的垂直平分线,
∴OA=OB,
则△AOB是等边三角形.
∴∠AOD=∠AOB=30°.同理∠AOE=30°.
∴∠DOE=∠AOD+∠AOE=60°.
故答案为60.
15.解:(1)连接OA,OB.
∵PA,PB分别是☉O的切线,
∴OA⊥PA,OB⊥PB,
即∠PAO=∠PBO=90°.
∵∠APB=80°,
∴在四边形OAPB中,∠AOB=360°-90°-90°-80°=100°,
∴∠ACB=∠AOB=50°.
(2)如图图,连接CE.
∵AE为☉O的直径,
∴∠ACE=90°.
由(1)知,∠ACB=50°,
∴∠BCE=∠ACE-∠ACB=40°,
∴∠BAE=∠BCE=40°.
∵在△ABD中,AB=AD,
∴∠ADB=∠ABD=70°.
∵∠ADB是△ACD的外角,
∴∠EAC=∠ADB-∠ACB=70°-50°=20°.
16.解:(1)如图图,过点D作DF⊥BC于点F.
∵AB为☉O的直径,∠A=∠B=90°,
∴四边形ABFD是矩形,AD与BC是☉O的切线,
∴DF=AB=2,BF=AD=2.
∵DE与☉O相切于点E,
∴DE=AD=2,CE=BC.
设BC=x,
则CF=BC-BF=x-2,DC=DE+CE=2+x.
在Rt△DCF中,DC2=CF2+DF2,
即(2+x)2=(x-2)2+(2)2,
解得x=,即BC的长为.
(2)∵AB为☉O的直径,∠BAD=∠B=90°,
∴AD∥BC,∴△ADE∽△GCE,
∴AD∶CG=DE∶CE=AE∶EG.
∵AD=DE=2,∴CG=CE=BC=,
∴BG=BC+CG=5,AE∶EG=4∶5.
在Rt△ABG中,AG==3,
∴EG=AG=.
知识点 切线长与切线长定理
1.如图7,P为☉O外一点,PA,PB分别切☉O于A,B两点.若PA=3,则PB的长度为 ( )
7
A.2 B.3 C.4 D.5
2.如图8,PA切☉O于点A,PB切☉O于点B,连接OP.若∠APO=30°,OA=2,则PB的长为 ( )
8
A. B. C.4 D.2
3.如图9,PA切☉O于点A,PB切☉O于点B,OP交☉O于点C,则下列结论中错误的是( )
9
A.∠1=∠2 B.PA=PB
C.AB⊥OP D.∠PAB=2∠1
4.如图0,从☉O外一点P引☉O的两条切线PA,PB,切点分别为A,B.若∠APB=60°,弦
AB=4,则PA= .
0
5.如图1,☉O的半径为3 cm,点P到圆心O的距离为6 cm,过点P引☉O的两条切线,这两条切线的夹角为 度.
1
6.[教材例5变式] 如图2 ,☉O内切于四边形ABCD,AB=10,CD=8,则AD+BC= .
2
7.如图3,AB,AC,BD是☉O的切线,P,C,D为切点.若AB=5,AC=3,则BD的长为 .
3
8.如图4,已知AB为☉O的直径,PA,PC是☉O的切线,A,C为切点,∠BAC=30°.
(1)求∠P的度数;
(2)若AB=2,求PA的长(结果保留根号).
4
9.如图5,AB是☉O的直径,过☉O外一点P作☉O的两条切线PC,PD,切点分别为C,D,连接OP,CD.
(1)求证:OP⊥CD;
(2)连接AD,BC,若∠DAB=50°,∠CBA=70°,OA=2,求OP的长.
5
10.如图6,PA,PB是☉O的切线,切点分别为A,B,OP交AB于点D,交☉O于点C,AB=4,DC=2,则∠APB的度数为 ( )
6
A.30° B.45° C.60° D.75°
11.如图7,PA,PB,CD分别切☉O于点A,B,E,CD分别交PA,PB于点C,D.若∠P=40°,则∠PAE+∠PBE的度数为 ( )
7
A.50° B.62° C.66° D.70°
12.如图8,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与☉O相切于E,F,G三点,过点D作☉O的切线交BC于点M,切点为N,则DM的长为 ( )
8
A. B. C. D.2
13.小明同学测量一个光盘的直径,他只有一把直尺和一个三角尺,他将直尺、光盘和三角尺按9所示方式放置于桌面上,并量出AB=3 cm,则此光盘的直径是 cm.
9
14.如图0,菱形ABOC的边AB,AC分别与☉O相切于点D,E.若D是AB的中点,则∠DOE= °.
0
15.已知PA,PB分别与☉O相切于点A,B,∠APB=80°,C为☉O上一点.
(1)如图1①,∠ACB的度数为 ;
(2)如图图②,AE为☉O的直径,AE与BC相交于点D,若AB=AD,求∠EAC的度数.
1
16.如图2①,已知AB为☉O的直径,∠A=∠B=90°,DE与☉O相切于点E,☉O的半径为,AD=2.
(1)BC的长为 ;
(2)如图图②,连接AE并延长交BC的延长线于点G,求EG的长.
2
答案
1.B
2.D ∵PA切☉O于点A,PB切☉O于点B,∴PA⊥OA,PB⊥OB,PA=PB.∵∠APO=30°,OA=2,∴OP=4,∴AP==2,∴BP=2.故选D.
3.D
4.4 ∵PA,PB是☉O的两条切线,∴PA=PB.又∵∠APB=60°,∴△PAB是等边三角形,∴PA=AB=4.
5.60
6.18 根据切线长定理,知AB+CD=AD+BC.
7.2 ∵AC,AP为☉O的切线,
∴AC=AP.
∵BP,BD为☉O的切线,∴BP=BD,
∴BD=BP=AB-AP=AB-AC=5-3=2.
故答案为2.
8.解:(1)∵PA是☉O的切线,AB为☉O的直径,
∴PA⊥AB,∴∠BAP=90°.
∵∠BAC=30°,∴∠CAP=90°-∠BAC=60°.
∵PA,PC分别切☉O于点A,C,∴PA=PC,
∴△PAC为等边三角形,∴∠P=60°.
(2)如图图,连接BC,则∠ACB=90°.
在Rt△ACB中,AB=2,∠BAC=30°,
∴AC=ABcos∠BAC=2cos30°=.
∵△PAC为等边三角形,∴PA=AC=.
9.解:(1)证明:如图图,连接OC,OD.
∵PD,PC是☉O的切线,∴PD=PC.
∵OD=OC,∴点P,O在CD的垂直平分线上,
∴OP⊥CD.
(2)如图图,连接AD,BC.
∵OA=OD=OC=OB=2,
∴∠ADO=∠DAO=50°,∠BCO=∠CBO=70°,
∴∠AOD=80°,∠BOC=40°,
∴∠COD=60°.
∵OD=OC,∴△COD是等边三角形.
∴∠DOP=∠COP=30°.
在Rt△ODP中,OP==.
10.C 连接AC,根据切线长定理,可得PA=PB,OP⊥AB,∴AD=AB=2,则tan∠ACD==,∴∠ACD=60°,∴△AOC是等边三角形,则∠AOP=60°,∴∠APO=30°,∴∠APB=60°.
11.D ∵PA,PB,CD分别切☉O于点A,B,E,CD分别交PA,PB于点C,D,
∴CE=CA,DE=DB,
∴∠CAE=∠CEA,∠DEB=∠DBE,
∴∠PCD=∠CAE+∠CEA=2∠CAE,∠PDC=∠DEB+∠DBE=2∠DBE,
∴∠CAE=∠PCD,∠DBE=∠PDC,
即∠PAE=∠PCD,∠PBE=∠PDC.
∵∠P=40°,
∴∠PAE+∠PBE=∠PCD+∠PDC=(∠PCD+∠PDC)=(180°-∠P)=70°.
故选D.
12.A 由题意可知AF=AE=BF=BG=2,DN=DE=3.设GM=x,则MN=x,DM=3+x,CM=3-x.在Rt△DMC中,∵DM2=CM2+CD2,即(3+x)2=(3-x)2+42,解得x=,∴DM=DN+MN=3+=.故选A.
13.6 如图图,连接OA,OB.
∵∠CAD=60°,
∴∠CAB=120°.
∵AB和AC与☉O相切,
∴∠OAB=∠OAC,
∴∠OAB=∠CAB=60°.
∵AB=3 cm,∴OA=6 cm.
在Rt△AOB中,由勾股定理,得OB=3 cm,
∴光盘的直径为6 cm.故答案为6.
14.60 如图图,连接OA.
∵四边形ABOC是菱形,
∴BA=BO.
∵AB与☉O相切于点D,
∴OD⊥AB.
∵D是AB的中点,
∴直线OD是线段AB的垂直平分线,
∴OA=OB,
则△AOB是等边三角形.
∴∠AOD=∠AOB=30°.同理∠AOE=30°.
∴∠DOE=∠AOD+∠AOE=60°.
故答案为60.
15.解:(1)连接OA,OB.
∵PA,PB分别是☉O的切线,
∴OA⊥PA,OB⊥PB,
即∠PAO=∠PBO=90°.
∵∠APB=80°,
∴在四边形OAPB中,∠AOB=360°-90°-90°-80°=100°,
∴∠ACB=∠AOB=50°.
(2)如图图,连接CE.
∵AE为☉O的直径,
∴∠ACE=90°.
由(1)知,∠ACB=50°,
∴∠BCE=∠ACE-∠ACB=40°,
∴∠BAE=∠BCE=40°.
∵在△ABD中,AB=AD,
∴∠ADB=∠ABD=70°.
∵∠ADB是△ACD的外角,
∴∠EAC=∠ADB-∠ACB=70°-50°=20°.
16.解:(1)如图图,过点D作DF⊥BC于点F.
∵AB为☉O的直径,∠A=∠B=90°,
∴四边形ABFD是矩形,AD与BC是☉O的切线,
∴DF=AB=2,BF=AD=2.
∵DE与☉O相切于点E,
∴DE=AD=2,CE=BC.
设BC=x,
则CF=BC-BF=x-2,DC=DE+CE=2+x.
在Rt△DCF中,DC2=CF2+DF2,
即(2+x)2=(x-2)2+(2)2,
解得x=,即BC的长为.
(2)∵AB为☉O的直径,∠BAD=∠B=90°,
∴AD∥BC,∴△ADE∽△GCE,
∴AD∶CG=DE∶CE=AE∶EG.
∵AD=DE=2,∴CG=CE=BC=,
∴BG=BC+CG=5,AE∶EG=4∶5.
在Rt△ABG中,AG==3,
∴EG=AG=.
