沪科版数学九年级下册同步课时练习:24.1 第1课时 旋转的概念及性质(word版含答案)
文档属性
| 名称 | 沪科版数学九年级下册同步课时练习:24.1 第1课时 旋转的概念及性质(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 252.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 00:00:00 | ||
图片预览


文档简介
24.1 第1课时 旋转的概念及性质
知识点 1 旋转变换及有关概念
1.下列运动中,不属于旋转的是 ( )
A.钟摆的运动
B.风力发电机风叶的转动
C.汽车方向盘的转动
D.观光电梯的升降运动
2.如图图24-1-1所示,△AOB绕着点O顺时针旋转至△A'OB',此时:
图24-1-1
(1)点B的对应点是点 ;
(2)旋转中心是点 ,旋转角为 ;
(3)∠A的对应角是 ,线段OB的对应线段是 .
3.在如图图24-1-2所示的方格纸中,△ABC的顶点都在格点(每个小方格的顶点叫做格点)上,将△ABC绕点O按顺时针方向旋转得到△A'B'C',使各顶点仍在格点上,则其旋转角的度数是 .
图24-1-2
知识点 2 旋转对称图形
4.已知平行四边形是旋转对称图形.如图图24-1-3,在平行四边形ABCD中,O是对角线AC,BD的交点,它的旋转中心是 ,至少旋转 度后能与自身重合.
图24-1-3
5.下列图形中,不是旋转对称图形的是 ( )
A B C D
图24-1-4
6.[教材练习第1题变式] 把图24-1-5中的交通标志图案绕着它的中心旋转一定角度后与自身重合,则这个旋转角度至少为 ( )
图24-1-5
A.30° B.90°
C.120° D.180°
知识点 3 旋转的性质
7.如图图24-1-6,△ODC是由△OAB绕点O顺时针旋转30°后得到的图形,点D在线段AB上.图中的相等线段有 ;
图24-1-6
图中等于30°的角有 ;图中的全等三角形是 .
8.如图图24-1-7,将△OAB绕点O逆时针旋转70°到△OCD的位置.若∠AOB=40°,则∠AOD的度数为 ( )
图24-1-7
A.45° B.40°
C.35° D.30°
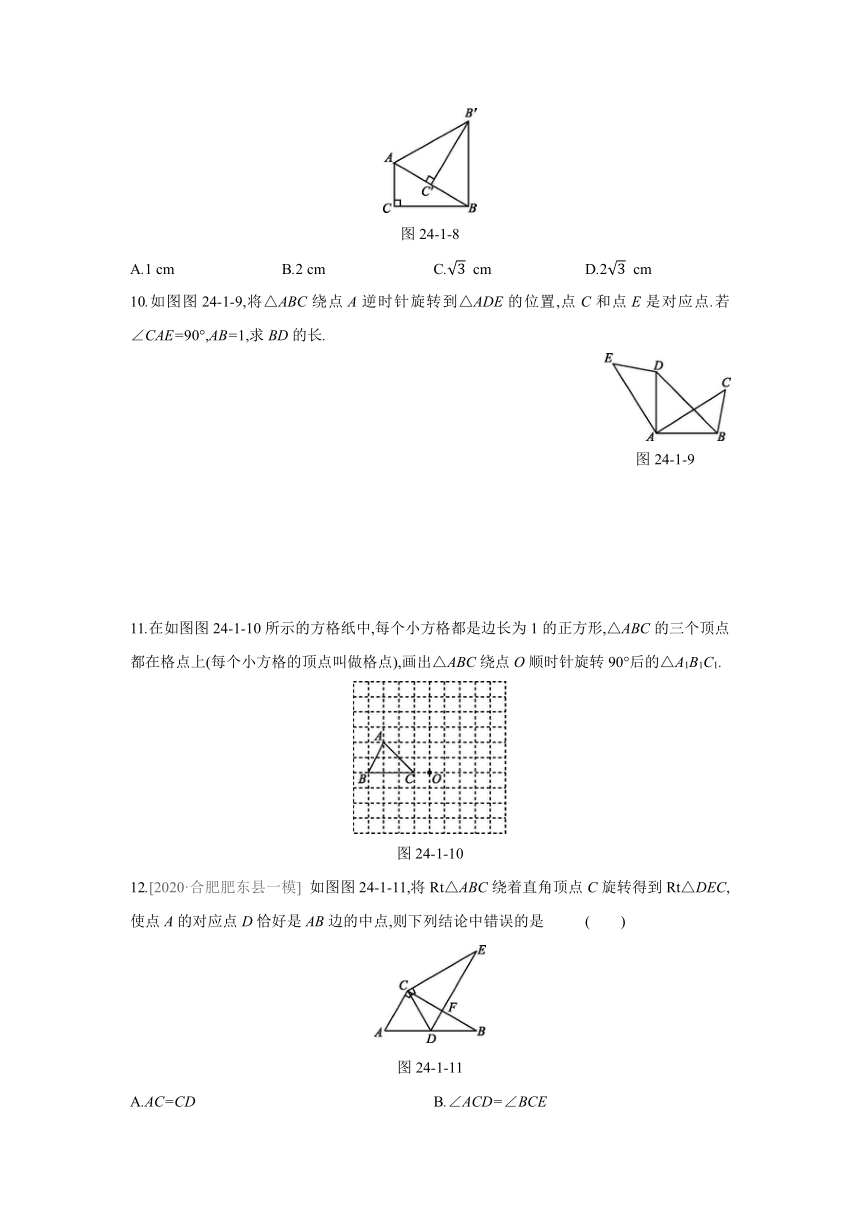
9.[2020·海南] 如图图24-1-8,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=1 cm,将Rt△ABC绕点A逆时针旋转得到Rt△AB'C',使点C'落在AB边上,连接BB',则BB'的长是 ( )
图24-1-8
A.1 cm B.2 cm C. cm D.2 cm
10.如图图24-1-9,将△ABC绕点A逆时针旋转到△ADE的位置,点C和点E是对应点.若∠CAE=90°,AB=1,求BD的长.
图24-1-9
11.在如图图24-1-10所示的方格纸中,每个小方格都是边长为1的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫做格点),画出△ABC绕点O顺时针旋转90°后的△A1B1C1.
图24-1-10
12.[2020·合肥肥东县一模] 如图图24-1-11,将Rt△ABC绕着直角顶点C旋转得到Rt△DEC,使点A的对应点D恰好是AB边的中点,则下列结论中错误的是 ( )
图24-1-11
A.AC=CD B.∠ACD=∠BCE
C.CD∶AB=1∶2 D.AC∶CE=1∶
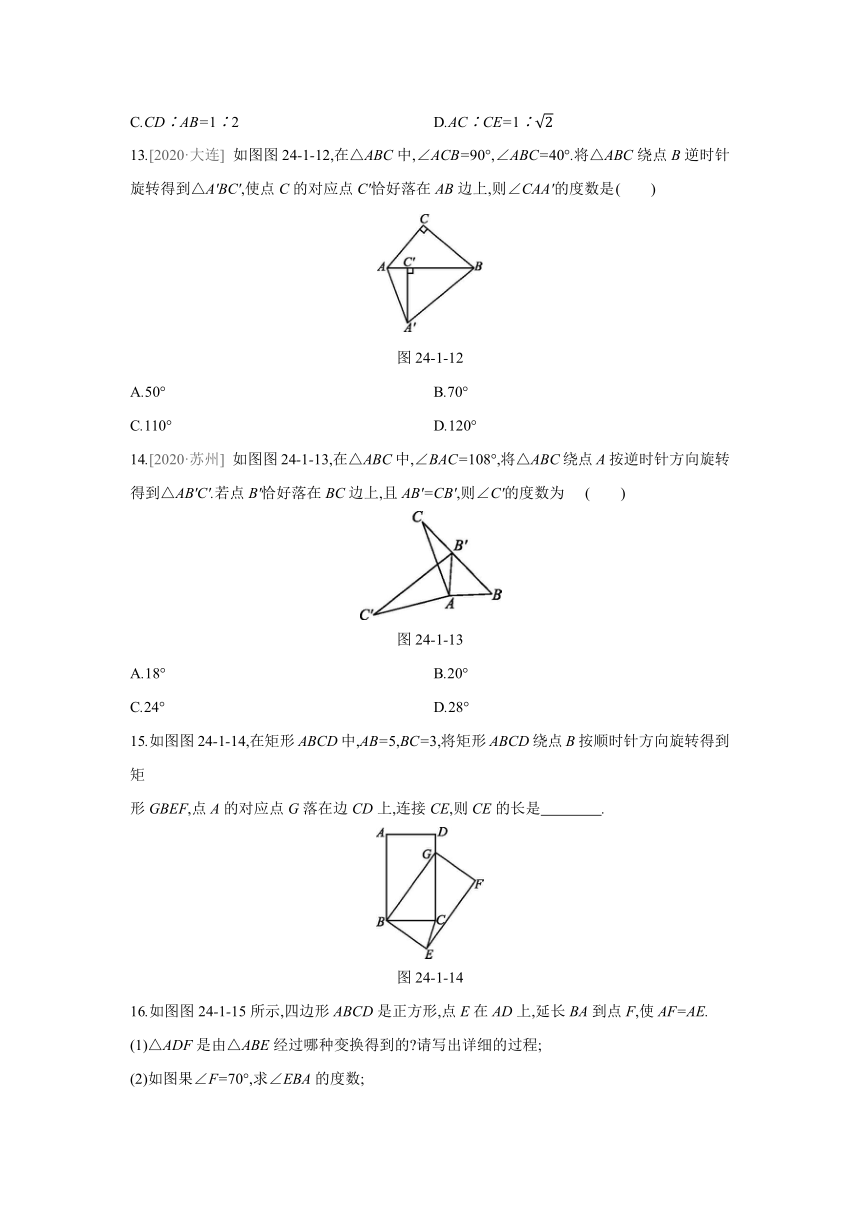
13.[2020·大连] 如图图24-1-12,在△ABC中,∠ACB=90°,∠ABC=40°.将△ABC绕点B逆时针旋转得到△A'BC',使点C的对应点C'恰好落在AB边上,则∠CAA'的度数是 ( )
图24-1-12
A.50° B.70°
C.110° D.120°
14.[2020·苏州] 如图图24-1-13,在△ABC中,∠BAC=108°,将△ABC绕点A按逆时针方向旋转得到△AB'C'.若点B'恰好落在BC边上,且AB'=CB',则∠C'的度数为 ( )
图24-1-13
A.18° B.20°
C.24° D.28°
15.如图图24-1-14,在矩形ABCD中,AB=5,BC=3,将矩形ABCD绕点B按顺时针方向旋转得到矩
形GBEF,点A的对应点G落在边CD上,连接CE,则CE的长是 .
图24-1-14
16.如图图24-1-15所示,四边形ABCD是正方形,点E在AD上,延长BA到点F,使AF=AE.
(1)△ADF是由△ABE经过哪种变换得到的 请写出详细的过程;
(2)如图果∠F=70°,求∠EBA的度数;
(3)试说明DF与BE的数量与位置关系.
图24-1-15
17.[2020·合肥庐阳区二模] 如图图24-1-16,在△ABC中,∠A=30°,∠ACB=90°,BC=2,D是AB上的动点,将线段CD绕点C逆时针旋转90°得到线段CE,连接BE,则BE的最小值是 ( )
图24-1-16
A.-1 B.
C. D.2
教师详解详析
1.D 对四个选项逐一分析,选项A,B,C都是旋转变换,选项D是平移变换.
2.(1)B' (2)O ∠AOA'或∠BOB'
(3)∠A' OB'
3.90° 根据旋转角的概念,可知∠BOB'是旋转角,且∠BOB'=90°.
4.点O 180 5.A 6.C
7.AO=DO,BO=CO,AB=DC
∠AOD,∠BOC,∠BDC △ODC≌△OAB
8.D 9.B
10.解:∵将△ABC绕点A逆时针旋转到△ADE,点C和点E是对应点,
∴AB=AD=1,∠BAD=∠CAE=90°,
∴BD===.
11.解:如图图,△A1B1C1即为所作.
12.D ∵将Rt△ABC绕着直角顶点C旋转得到Rt△DEC,
∴△ABC≌△DEC,
∴AC=CD,故A选项正确;
∵D恰好是AB边的中点,
∴CD=AD=DB=AB,
故C选项正确;
由旋转的性质可知,∠ACB=∠DCE,
∴∠ACD=∠BCE,故B选项正确;
∵AC=CD=AD,
∴△ACD为等边三角形,
∴∠A=60°,∴=.
∵CE=BC,∴AC∶CE=1∶,
故D选项错误.
故选D.
13.D ∵∠ACB=90°,∠ABC=40°,
∴∠CAB=90°-40°=50°.
由旋转的性质可知,∠A'BA=∠ABC=40°,A'B=AB,
∴∠BAA'=∠BA'A=(180°-40°)=70°,
∴∠CAA'=∠CAB+∠BAA'=50°+70°=120°.
故选D.
14.C ∵AB'=CB',
∴∠C=∠CAB',
∴∠AB'B=∠C+∠CAB'=2∠C.
∵将△ABC绕点A按逆时针方向旋转得到△AB'C',
∴∠C=∠C',AB=AB',
∴∠B=∠AB'B=2∠C.
∵∠B+∠C+∠CAB=180°,∠CAB=108°,
∴3∠C=180°-108°,
∴∠C=24°,∴∠C'=∠C=24°.
故选C.
15. 如图图,连接AG.
由旋转变换的性质可知,∠ABG=∠CBE,BA=BG=5,BC=BE=3.
由勾股定理,得CG==4,
∴DG=DC-CG=1,
则AG==.
∵=,∠ABG=∠CBE,
∴△ABG∽△CBE,
∴==,
∴CE=.
16.解:(1)△ADF是由△ABE绕点A逆时针旋转90°得到的.
(2)∵△ADF是由△ABE旋转得到的,
∴由图形旋转的性质知∠EBA=∠FDA=90°-70°=20°.
(3)如图图,延长BE交DF于点G,则∠AEB=∠DEG.
由(1)可知∠EBA=∠ADF,
∴∠EGD=180°-∠ADF-∠DEG=180°-∠EBA-∠AEB=∠DAB=90°,
∴DF与BE垂直.
又由旋转的性质知DF=BE,
∴DF与BE垂直且相等.
17.A 如图图,在AC上截取CF=2,连接DF,则CF=BC.
由题意,得AC==2.
∵将线段CD绕点C逆时针旋转90°得到线段CE,
∴CD=CE,∠DCE=90°.
又∵∠ACB=90°,∴∠FCD=∠BCE,
∴△FCD≌△BCE,∴BE=FD.
当FD⊥AB时,FD最小,此时FD=AF=(AC-CF)=×(2-2)=-1.
故选A.
知识点 1 旋转变换及有关概念
1.下列运动中,不属于旋转的是 ( )
A.钟摆的运动
B.风力发电机风叶的转动
C.汽车方向盘的转动
D.观光电梯的升降运动
2.如图图24-1-1所示,△AOB绕着点O顺时针旋转至△A'OB',此时:
图24-1-1
(1)点B的对应点是点 ;
(2)旋转中心是点 ,旋转角为 ;
(3)∠A的对应角是 ,线段OB的对应线段是 .
3.在如图图24-1-2所示的方格纸中,△ABC的顶点都在格点(每个小方格的顶点叫做格点)上,将△ABC绕点O按顺时针方向旋转得到△A'B'C',使各顶点仍在格点上,则其旋转角的度数是 .
图24-1-2
知识点 2 旋转对称图形
4.已知平行四边形是旋转对称图形.如图图24-1-3,在平行四边形ABCD中,O是对角线AC,BD的交点,它的旋转中心是 ,至少旋转 度后能与自身重合.
图24-1-3
5.下列图形中,不是旋转对称图形的是 ( )
A B C D
图24-1-4
6.[教材练习第1题变式] 把图24-1-5中的交通标志图案绕着它的中心旋转一定角度后与自身重合,则这个旋转角度至少为 ( )
图24-1-5
A.30° B.90°
C.120° D.180°
知识点 3 旋转的性质
7.如图图24-1-6,△ODC是由△OAB绕点O顺时针旋转30°后得到的图形,点D在线段AB上.图中的相等线段有 ;
图24-1-6
图中等于30°的角有 ;图中的全等三角形是 .
8.如图图24-1-7,将△OAB绕点O逆时针旋转70°到△OCD的位置.若∠AOB=40°,则∠AOD的度数为 ( )
图24-1-7
A.45° B.40°
C.35° D.30°
9.[2020·海南] 如图图24-1-8,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=1 cm,将Rt△ABC绕点A逆时针旋转得到Rt△AB'C',使点C'落在AB边上,连接BB',则BB'的长是 ( )
图24-1-8
A.1 cm B.2 cm C. cm D.2 cm
10.如图图24-1-9,将△ABC绕点A逆时针旋转到△ADE的位置,点C和点E是对应点.若∠CAE=90°,AB=1,求BD的长.
图24-1-9
11.在如图图24-1-10所示的方格纸中,每个小方格都是边长为1的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫做格点),画出△ABC绕点O顺时针旋转90°后的△A1B1C1.
图24-1-10
12.[2020·合肥肥东县一模] 如图图24-1-11,将Rt△ABC绕着直角顶点C旋转得到Rt△DEC,使点A的对应点D恰好是AB边的中点,则下列结论中错误的是 ( )
图24-1-11
A.AC=CD B.∠ACD=∠BCE
C.CD∶AB=1∶2 D.AC∶CE=1∶
13.[2020·大连] 如图图24-1-12,在△ABC中,∠ACB=90°,∠ABC=40°.将△ABC绕点B逆时针旋转得到△A'BC',使点C的对应点C'恰好落在AB边上,则∠CAA'的度数是 ( )
图24-1-12
A.50° B.70°
C.110° D.120°
14.[2020·苏州] 如图图24-1-13,在△ABC中,∠BAC=108°,将△ABC绕点A按逆时针方向旋转得到△AB'C'.若点B'恰好落在BC边上,且AB'=CB',则∠C'的度数为 ( )
图24-1-13
A.18° B.20°
C.24° D.28°
15.如图图24-1-14,在矩形ABCD中,AB=5,BC=3,将矩形ABCD绕点B按顺时针方向旋转得到矩
形GBEF,点A的对应点G落在边CD上,连接CE,则CE的长是 .
图24-1-14
16.如图图24-1-15所示,四边形ABCD是正方形,点E在AD上,延长BA到点F,使AF=AE.
(1)△ADF是由△ABE经过哪种变换得到的 请写出详细的过程;
(2)如图果∠F=70°,求∠EBA的度数;
(3)试说明DF与BE的数量与位置关系.
图24-1-15
17.[2020·合肥庐阳区二模] 如图图24-1-16,在△ABC中,∠A=30°,∠ACB=90°,BC=2,D是AB上的动点,将线段CD绕点C逆时针旋转90°得到线段CE,连接BE,则BE的最小值是 ( )
图24-1-16
A.-1 B.
C. D.2
教师详解详析
1.D 对四个选项逐一分析,选项A,B,C都是旋转变换,选项D是平移变换.
2.(1)B' (2)O ∠AOA'或∠BOB'
(3)∠A' OB'
3.90° 根据旋转角的概念,可知∠BOB'是旋转角,且∠BOB'=90°.
4.点O 180 5.A 6.C
7.AO=DO,BO=CO,AB=DC
∠AOD,∠BOC,∠BDC △ODC≌△OAB
8.D 9.B
10.解:∵将△ABC绕点A逆时针旋转到△ADE,点C和点E是对应点,
∴AB=AD=1,∠BAD=∠CAE=90°,
∴BD===.
11.解:如图图,△A1B1C1即为所作.
12.D ∵将Rt△ABC绕着直角顶点C旋转得到Rt△DEC,
∴△ABC≌△DEC,
∴AC=CD,故A选项正确;
∵D恰好是AB边的中点,
∴CD=AD=DB=AB,
故C选项正确;
由旋转的性质可知,∠ACB=∠DCE,
∴∠ACD=∠BCE,故B选项正确;
∵AC=CD=AD,
∴△ACD为等边三角形,
∴∠A=60°,∴=.
∵CE=BC,∴AC∶CE=1∶,
故D选项错误.
故选D.
13.D ∵∠ACB=90°,∠ABC=40°,
∴∠CAB=90°-40°=50°.
由旋转的性质可知,∠A'BA=∠ABC=40°,A'B=AB,
∴∠BAA'=∠BA'A=(180°-40°)=70°,
∴∠CAA'=∠CAB+∠BAA'=50°+70°=120°.
故选D.
14.C ∵AB'=CB',
∴∠C=∠CAB',
∴∠AB'B=∠C+∠CAB'=2∠C.
∵将△ABC绕点A按逆时针方向旋转得到△AB'C',
∴∠C=∠C',AB=AB',
∴∠B=∠AB'B=2∠C.
∵∠B+∠C+∠CAB=180°,∠CAB=108°,
∴3∠C=180°-108°,
∴∠C=24°,∴∠C'=∠C=24°.
故选C.
15. 如图图,连接AG.
由旋转变换的性质可知,∠ABG=∠CBE,BA=BG=5,BC=BE=3.
由勾股定理,得CG==4,
∴DG=DC-CG=1,
则AG==.
∵=,∠ABG=∠CBE,
∴△ABG∽△CBE,
∴==,
∴CE=.
16.解:(1)△ADF是由△ABE绕点A逆时针旋转90°得到的.
(2)∵△ADF是由△ABE旋转得到的,
∴由图形旋转的性质知∠EBA=∠FDA=90°-70°=20°.
(3)如图图,延长BE交DF于点G,则∠AEB=∠DEG.
由(1)可知∠EBA=∠ADF,
∴∠EGD=180°-∠ADF-∠DEG=180°-∠EBA-∠AEB=∠DAB=90°,
∴DF与BE垂直.
又由旋转的性质知DF=BE,
∴DF与BE垂直且相等.
17.A 如图图,在AC上截取CF=2,连接DF,则CF=BC.
由题意,得AC==2.
∵将线段CD绕点C逆时针旋转90°得到线段CE,
∴CD=CE,∠DCE=90°.
又∵∠ACB=90°,∴∠FCD=∠BCE,
∴△FCD≌△BCE,∴BE=FD.
当FD⊥AB时,FD最小,此时FD=AF=(AC-CF)=×(2-2)=-1.
故选A.
