青岛版八年级数学上册1.2怎样判定三角形全等第2课时课件(共16张PPT)
文档属性
| 名称 | 青岛版八年级数学上册1.2怎样判定三角形全等第2课时课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 661.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 18:17:27 | ||
图片预览





文档简介
(共16张PPT)
1.2怎样判定三角形全等(2)
复习
2、我们学习了哪些判定三角形全等的方法?
(1)定义
(2)SAS
1、什么是全等三角形?
能够完全重合的两个三角形叫做全等三角形.
课题引入
问题: 如图,小明、小强一起踢球,不小心把一
块三角形的装饰玻璃踢碎了,摔成了3 块,两人决定赔
偿.你能告诉他们只带其中哪一块去玻璃店,就可以买
到一块完全一样的玻璃吗?
3
2
1
大家一起做下面的实验:
1、用刻度尺画AB=8cm;
2、在AB同侧作∠MAB=45°,∠NBA=60°;
3、射线AM与BN的交点记作点C.
把所做的三角形剪下来,与小组同学的进行比较,它们全等吗?
由此你得出什么结论?
实验与探究
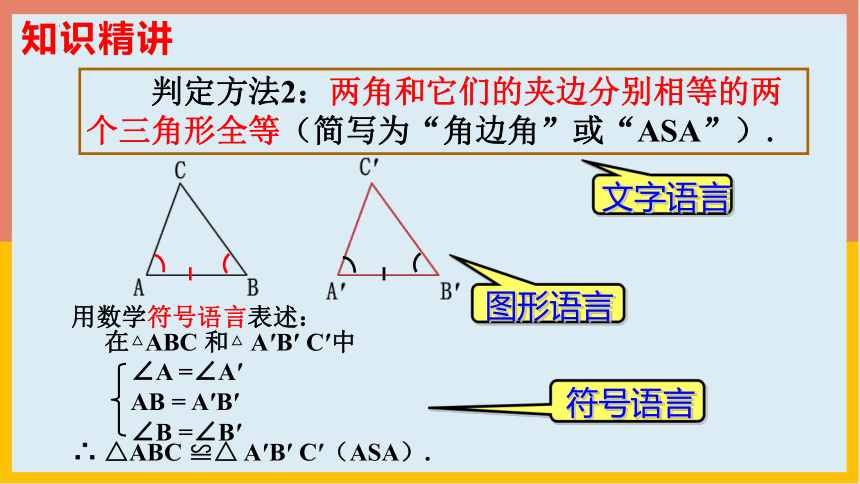
判定方法2:两角和它们的夹边分别相等的两个三角形全等(简写为“角边角”或“ASA”).
用数学符号语言表述:
在△ABC 和△ A′B′ C′中
∴ △ABC ≌△ A′B′ C′(ASA).
∠A =∠A′
AB = A′B′
∠B =∠B′
文字语言
符号语言
图形语言
知识精讲
例3
已知∠ACB=∠DFE,∠B=∠E,BC=EF,那么△ABC与△DEF全等吗?为什么?
例题讲解
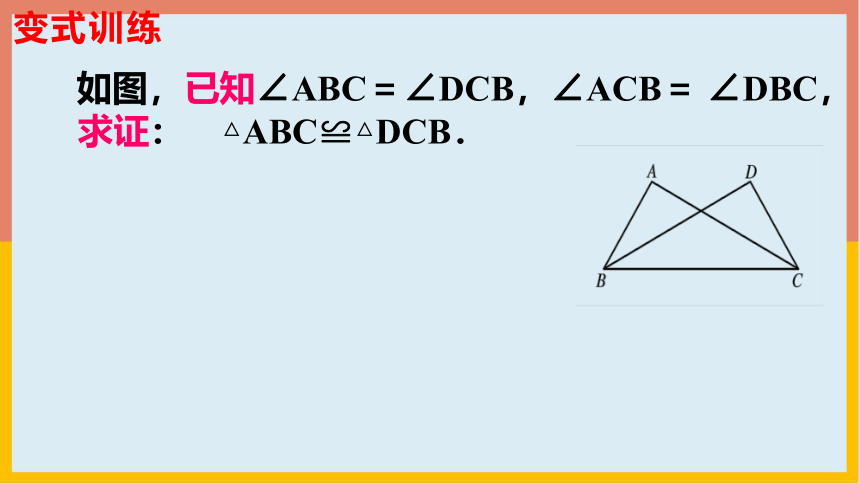
如图,已知∠ABC=∠DCB,∠ACB= ∠DBC,
求证: △ABC≌△DCB.
变式训练
C
B
A
C
B
A
3、△ABC与△A B C 全等吗?为什么?
交流与发现
1、如图:在△ABC与△A B C 中,BC=B C ,∠B=∠B ,如果∠A=∠A ,这时边BC与∠A什么关系?边B C 与∠A 呢?
2、∠C与∠C 相等吗?为什么?
4、由此你能得出什么结论?
用符号语言表达为:
A
B
C
A′
B′
C′
判定方法3:两角分别相等且其中一组等角的对边也相等的两个三角形全等.(简写为“角角边”或“AAS”).
在△ABC 与 △ A′B′C ′中,
∠A =∠A′ ,
∠B =∠B′ ,
BC =B′C ′ ,
∵
∴ △ABC ≌△A′B′C ′ (AAS).
例4
1
4
3
2
A
D
C
B
在△ABD 与△CDB中,已知∠A=∠C,再添加一个什么条件,就可以判定△ABD 与△CDB全等?说明理由
例题讲解
如图,∠1=∠2,∠3=∠4
试说明:AC=AD
C
A
D
1
B
2
3
4
变式训练
小亮在学习了全等三角形的判定方法2和判定方法3后,他发现在这两个判定方法的条件中,相等的边可以是“两等角的夹边”,也可以是“一组等角的对边”,于是,他认为可以把这两个判定概括成“满足两角及一边分别相等的两个三角形全等”.你同意他的意见吗?如果不同意,请举例说明.
挑战自我
A
B
C
D
观
察
如图:△ABC是直角三角形,
∠ACB=90o ,CD AB,垂足为D。
则在△ACD与△CBD中便有:
∠A= ∠1
∠ADC= ∠CDB=90o
CD=CD
试想△ACD与△CBD会全等吗?
(
1
两个三角形并非有两角一边对应相等便能判别它们全等,只有满足(ASA)和(AAS)才行。
挑战自我
小结
通过本节课的内容,你有哪些收获?
三角形全等判定方法
SAS
ASA
AAS
?
课堂总结
课本16页习题1.2,第4,5题。
布置作业
1.2怎样判定三角形全等(2)
复习
2、我们学习了哪些判定三角形全等的方法?
(1)定义
(2)SAS
1、什么是全等三角形?
能够完全重合的两个三角形叫做全等三角形.
课题引入
问题: 如图,小明、小强一起踢球,不小心把一
块三角形的装饰玻璃踢碎了,摔成了3 块,两人决定赔
偿.你能告诉他们只带其中哪一块去玻璃店,就可以买
到一块完全一样的玻璃吗?
3
2
1
大家一起做下面的实验:
1、用刻度尺画AB=8cm;
2、在AB同侧作∠MAB=45°,∠NBA=60°;
3、射线AM与BN的交点记作点C.
把所做的三角形剪下来,与小组同学的进行比较,它们全等吗?
由此你得出什么结论?
实验与探究
判定方法2:两角和它们的夹边分别相等的两个三角形全等(简写为“角边角”或“ASA”).
用数学符号语言表述:
在△ABC 和△ A′B′ C′中
∴ △ABC ≌△ A′B′ C′(ASA).
∠A =∠A′
AB = A′B′
∠B =∠B′
文字语言
符号语言
图形语言
知识精讲
例3
已知∠ACB=∠DFE,∠B=∠E,BC=EF,那么△ABC与△DEF全等吗?为什么?
例题讲解
如图,已知∠ABC=∠DCB,∠ACB= ∠DBC,
求证: △ABC≌△DCB.
变式训练
C
B
A
C
B
A
3、△ABC与△A B C 全等吗?为什么?
交流与发现
1、如图:在△ABC与△A B C 中,BC=B C ,∠B=∠B ,如果∠A=∠A ,这时边BC与∠A什么关系?边B C 与∠A 呢?
2、∠C与∠C 相等吗?为什么?
4、由此你能得出什么结论?
用符号语言表达为:
A
B
C
A′
B′
C′
判定方法3:两角分别相等且其中一组等角的对边也相等的两个三角形全等.(简写为“角角边”或“AAS”).
在△ABC 与 △ A′B′C ′中,
∠A =∠A′ ,
∠B =∠B′ ,
BC =B′C ′ ,
∵
∴ △ABC ≌△A′B′C ′ (AAS).
例4
1
4
3
2
A
D
C
B
在△ABD 与△CDB中,已知∠A=∠C,再添加一个什么条件,就可以判定△ABD 与△CDB全等?说明理由
例题讲解
如图,∠1=∠2,∠3=∠4
试说明:AC=AD
C
A
D
1
B
2
3
4
变式训练
小亮在学习了全等三角形的判定方法2和判定方法3后,他发现在这两个判定方法的条件中,相等的边可以是“两等角的夹边”,也可以是“一组等角的对边”,于是,他认为可以把这两个判定概括成“满足两角及一边分别相等的两个三角形全等”.你同意他的意见吗?如果不同意,请举例说明.
挑战自我
A
B
C
D
观
察
如图:△ABC是直角三角形,
∠ACB=90o ,CD AB,垂足为D。
则在△ACD与△CBD中便有:
∠A= ∠1
∠ADC= ∠CDB=90o
CD=CD
试想△ACD与△CBD会全等吗?
(
1
两个三角形并非有两角一边对应相等便能判别它们全等,只有满足(ASA)和(AAS)才行。
挑战自我
小结
通过本节课的内容,你有哪些收获?
三角形全等判定方法
SAS
ASA
AAS
?
课堂总结
课本16页习题1.2,第4,5题。
布置作业
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
