北师大版数学七年级下册5.3.2垂直平分线的性质课件(共24张PPT)
文档属性
| 名称 | 北师大版数学七年级下册5.3.2垂直平分线的性质课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 360.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 18:24:49 | ||
图片预览







文档简介
(共24张PPT)
5.3 简单的轴对称图形
第五章 生活中的轴对称
2 线段垂直平分线的性质
温故知新
等边三角形的性质:
等腰三角形的特征
学习目标
1.理解线段的垂直平分线的概念;
2.理解并掌握线段垂直平分线的性质.(重点)
3.用尺规作出线段的垂直平分线.(重点)
4.能够运用线段垂直平分线的性质解决实际题.
(难点)
新知探究
线段是轴对称图形吗?如果是,你能找出它的一条对称轴吗?这条对称轴与线段存在着什么关系?
A
B
问题引入
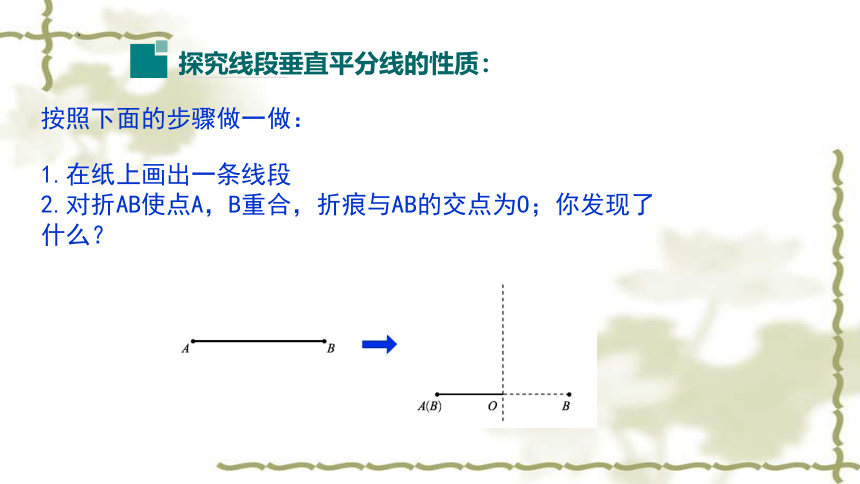
按照下面的步骤做一做:
折痕与AB的交点为O;
探究线段垂直平分线的性质:
1.在纸上画出一条线段
2.对折AB使点A,B重合,折痕与AB的交点为O;你发现了什么?
探究线段垂直平分线的性质:
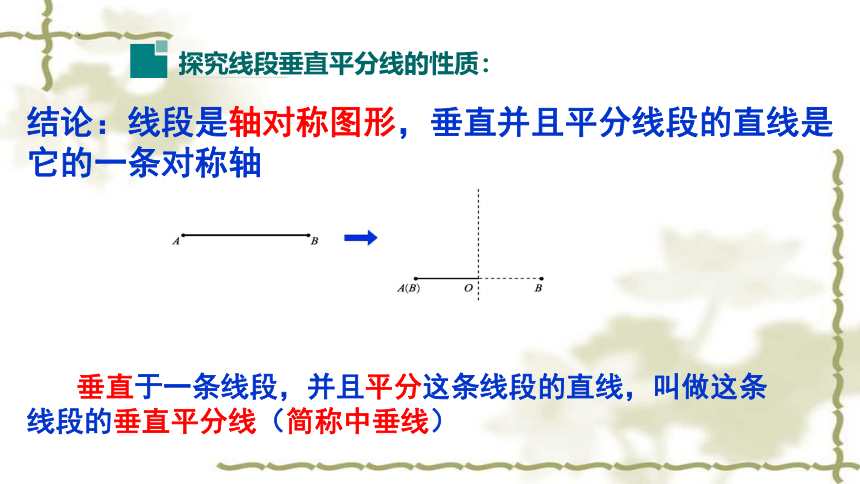
结论:线段是轴对称图形,垂直并且平分线段的直线是
它的一条对称轴
垂直于一条线段,并且平分这条线段的直线,叫做这条线段的垂直平分线(简称中垂线)
在刚刚的折痕上任取一点C,即C是线段AB垂直平分线上的一点,思考:
线段的垂直平分线性质
A
B
C
O
(1)OC与AB具有怎样的位置关系?
(2)AC与BC相等吗?
(3)改变点C的位置,结论还成立吗?
探究新知
在刚刚的折痕上任取一点C,即C是线段AB垂直平分线上的一点,思考:
线段的垂直平分线性质
A
B
C
O
(1)OC与AB具有怎样的位置关系?
(2)AC与BC相等吗?
(3)改变点C的位置,结论还成立吗?
(1)垂直
(2)相等
(3)无论C点取在直线的何处,线段AC和BC都相等
探究新知
线段的垂直平分线性质
A
B
C
O
1.线段垂直平分线上的点到这条线段的两个端点的距离相等.
2.线段的垂直平分线经过线段的中点且垂直于这条线段.
数学语言
∵点C在线段AB的垂直平分线上
∴AC = BC
例1 如图,DE是AC的垂直平分线,AB=12厘米,
BC=10厘米,则△BCD的周长为( )
A.22厘米 B.16厘米
C.26厘米 D.25厘米
解析:根据线段垂直平分线的性质
得CD=AD,
故△BCD的周长为
BD+DC+BC=AD+BD+BC=AB+BC
=12+10
=22(厘米).
A
典例精析
例1 利用尺规,作线段AB的垂直平分线.
已知:线段AB.
求作:AB的垂直平分线.
A
B
典例精析
例1 利用尺规,作线段AB的垂直平分线.
作法:
1.分别以点A和点B为圆心,以大于
AB的长为半径作弧,两弧相交于点C和D;
已知:线段AB.
求作:AB的垂直平分线.
2.作直线CD.
直线CD就是线段AB的垂直平分线.
A
B
C
D
做一做
利用尺规作如图所示的△ABC的重心,
并测量这个点到三个顶点的距离,有什么发现?
B
C
A
做一做
利用尺规作如图所示的△ABC的重心。
解:如图所示,点G即为所求。
这个点到它三个顶点的距离相等。
作法如下:
1:分别以点A和点B为圆心,以大于 AB的长为半径作弧,两弧相交于点M和N,作直线MN,
2:同理作出边BC的中线EF;
3: MN,EF的交点G即为所求。
例2 如图,某地由于居民增多,要在公路l边增加一个公共汽车站,A,B是路边两个新建小区,这个公共汽车站C建在什么位置,能使两个小区到车站的路程一样长(要求:尺规作图,保留作图痕迹,不写画法)
解:连接AB,作AB的垂直平分线交直线l于O,交AB于E.∵EO是线段AB的垂直平分线,∴点O到A,B的距离相等,∴这个公共汽车站C应建在O点处,才能使到两个小区的路程一样长.
1.如图,等腰△ABC中,AB=AC,∠A=40°,线段AB的垂直平分线交AB于D,交AC于E,连接BE,则∠CBE等于( )
A.60° B.50° C.40° D.30°
D
解:∵DE是△ABC边AB的垂直平分线,
∴EB=EA,
∴△AEC的周长=AC+CE+EA
=AC+CE+EB
=AC+BC
又∵AC=4,BC=5
因此△AEC的周长=4+5=9
2.如图,DE是△ABC边AB的垂直平分线,交AB、
BC于D、E,若AC=4,BC=5,求△AEC的周长.
A
D
B
E
C
课堂小结
1.经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线(也叫中垂线)
2.线段垂直平分线上的点与这条线段两个端点的距离相等
注意:
(1)线段的垂直平分线(也称为中垂线)是直线而不是线段.
(2)线段是轴对称图形,垂直并且平分线段的直线是它的一条对称轴
当堂检测
5.3 简单的轴对称图形
第五章 生活中的轴对称
2 线段垂直平分线的性质
温故知新
等边三角形的性质:
等腰三角形的特征
学习目标
1.理解线段的垂直平分线的概念;
2.理解并掌握线段垂直平分线的性质.(重点)
3.用尺规作出线段的垂直平分线.(重点)
4.能够运用线段垂直平分线的性质解决实际题.
(难点)
新知探究
线段是轴对称图形吗?如果是,你能找出它的一条对称轴吗?这条对称轴与线段存在着什么关系?
A
B
问题引入
按照下面的步骤做一做:
折痕与AB的交点为O;
探究线段垂直平分线的性质:
1.在纸上画出一条线段
2.对折AB使点A,B重合,折痕与AB的交点为O;你发现了什么?
探究线段垂直平分线的性质:
结论:线段是轴对称图形,垂直并且平分线段的直线是
它的一条对称轴
垂直于一条线段,并且平分这条线段的直线,叫做这条线段的垂直平分线(简称中垂线)
在刚刚的折痕上任取一点C,即C是线段AB垂直平分线上的一点,思考:
线段的垂直平分线性质
A
B
C
O
(1)OC与AB具有怎样的位置关系?
(2)AC与BC相等吗?
(3)改变点C的位置,结论还成立吗?
探究新知
在刚刚的折痕上任取一点C,即C是线段AB垂直平分线上的一点,思考:
线段的垂直平分线性质
A
B
C
O
(1)OC与AB具有怎样的位置关系?
(2)AC与BC相等吗?
(3)改变点C的位置,结论还成立吗?
(1)垂直
(2)相等
(3)无论C点取在直线的何处,线段AC和BC都相等
探究新知
线段的垂直平分线性质
A
B
C
O
1.线段垂直平分线上的点到这条线段的两个端点的距离相等.
2.线段的垂直平分线经过线段的中点且垂直于这条线段.
数学语言
∵点C在线段AB的垂直平分线上
∴AC = BC
例1 如图,DE是AC的垂直平分线,AB=12厘米,
BC=10厘米,则△BCD的周长为( )
A.22厘米 B.16厘米
C.26厘米 D.25厘米
解析:根据线段垂直平分线的性质
得CD=AD,
故△BCD的周长为
BD+DC+BC=AD+BD+BC=AB+BC
=12+10
=22(厘米).
A
典例精析
例1 利用尺规,作线段AB的垂直平分线.
已知:线段AB.
求作:AB的垂直平分线.
A
B
典例精析
例1 利用尺规,作线段AB的垂直平分线.
作法:
1.分别以点A和点B为圆心,以大于
AB的长为半径作弧,两弧相交于点C和D;
已知:线段AB.
求作:AB的垂直平分线.
2.作直线CD.
直线CD就是线段AB的垂直平分线.
A
B
C
D
做一做
利用尺规作如图所示的△ABC的重心,
并测量这个点到三个顶点的距离,有什么发现?
B
C
A
做一做
利用尺规作如图所示的△ABC的重心。
解:如图所示,点G即为所求。
这个点到它三个顶点的距离相等。
作法如下:
1:分别以点A和点B为圆心,以大于 AB的长为半径作弧,两弧相交于点M和N,作直线MN,
2:同理作出边BC的中线EF;
3: MN,EF的交点G即为所求。
例2 如图,某地由于居民增多,要在公路l边增加一个公共汽车站,A,B是路边两个新建小区,这个公共汽车站C建在什么位置,能使两个小区到车站的路程一样长(要求:尺规作图,保留作图痕迹,不写画法)
解:连接AB,作AB的垂直平分线交直线l于O,交AB于E.∵EO是线段AB的垂直平分线,∴点O到A,B的距离相等,∴这个公共汽车站C应建在O点处,才能使到两个小区的路程一样长.
1.如图,等腰△ABC中,AB=AC,∠A=40°,线段AB的垂直平分线交AB于D,交AC于E,连接BE,则∠CBE等于( )
A.60° B.50° C.40° D.30°
D
解:∵DE是△ABC边AB的垂直平分线,
∴EB=EA,
∴△AEC的周长=AC+CE+EA
=AC+CE+EB
=AC+BC
又∵AC=4,BC=5
因此△AEC的周长=4+5=9
2.如图,DE是△ABC边AB的垂直平分线,交AB、
BC于D、E,若AC=4,BC=5,求△AEC的周长.
A
D
B
E
C
课堂小结
1.经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线(也叫中垂线)
2.线段垂直平分线上的点与这条线段两个端点的距离相等
注意:
(1)线段的垂直平分线(也称为中垂线)是直线而不是线段.
(2)线段是轴对称图形,垂直并且平分线段的直线是它的一条对称轴
当堂检测
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
