沪科版按数学七年级下底8章复习(整式中求阴影图形面积的数学思想) 课件(共26张PPT)
文档属性
| 名称 | 沪科版按数学七年级下底8章复习(整式中求阴影图形面积的数学思想) 课件(共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 587.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-17 08:49:33 | ||
图片预览



文档简介
(共26张PPT)
整式中求阴影图形面积的数学思想
沪科版数学七年级下册
第八章 本章复习与测试
1、运用整体的思想
1.1
把分散的图形重新组合成整体
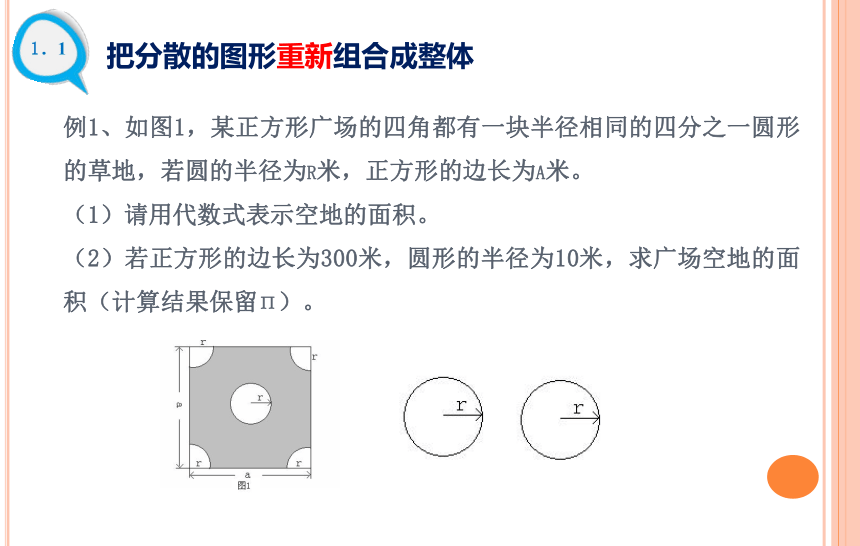
例1、如图1,某正方形广场的四角都有一块半径相同的四分之一圆形的草地,若圆的半径为r米,正方形的边长为a米。
(1)请用代数式表示空地的面积。
(2)若正方形的边长为300米,圆形的半径为10米,求广场空地的面积(计算结果保留π)。
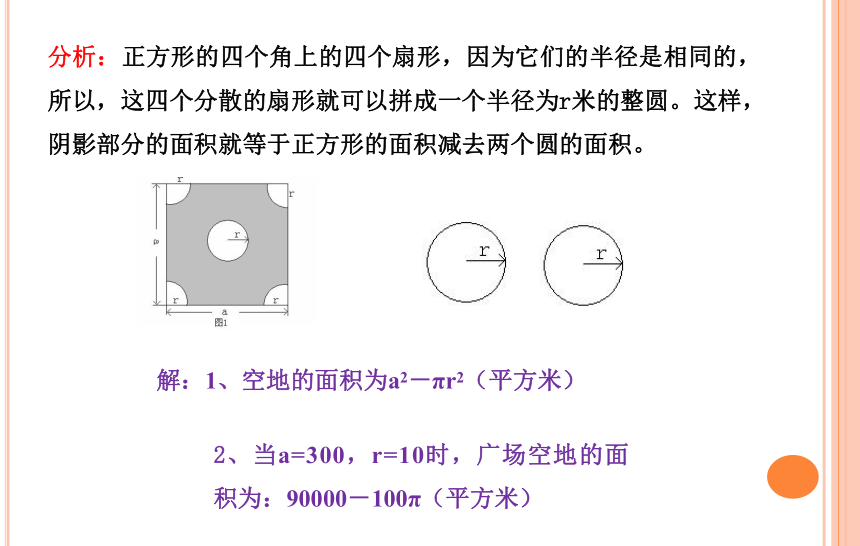
分析:正方形的四个角上的四个扇形,因为它们的半径是相同的,所以,这四个分散的扇形就可以拼成一个半径为r米的整圆。这样,阴影部分的面积就等于正方形的面积减去两个圆的面积。
解:1、空地的面积为a2-πr2(平方米)
2、当a=300,r=10时,广场空地的面积为:90000-100π(平方米)
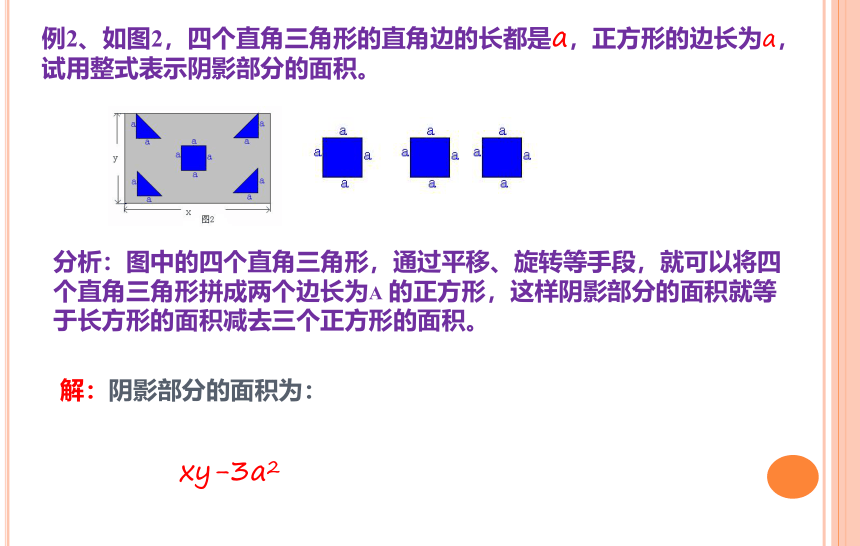
例2、如图2,四个直角三角形的直角边的长都是a,正方形的边长为a,试用整式表示阴影部分的面积。
分析:图中的四个直角三角形,通过平移、旋转等手段,就可以将四个直角三角形拼成两个边长为a 的正方形,这样阴影部分的面积就等于长方形的面积减去三个正方形的面积。
解:阴影部分的面积为:
xy-3a2
1.2
把不完整的图形补成整体
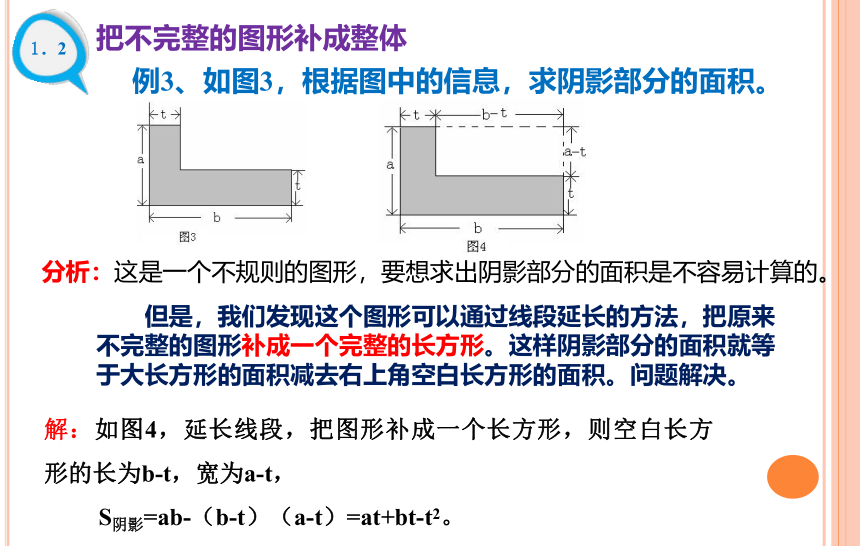
例3、如图3,根据图中的信息,求阴影部分的面积。
分析:这是一个不规则的图形,要想求出阴影部分的面积是不容易计算的。
但是,我们发现这个图形可以通过线段延长的方法,把原来不完整的图形补成一个完整的长方形。这样阴影部分的面积就等于大长方形的面积减去右上角空白长方形的面积。问题解决。
解:如图4,延长线段,把图形补成一个长方形,则空白长方形的长为b-t,宽为a-t,
S阴影=ab-(b-t)(a-t)=at+bt-t2。
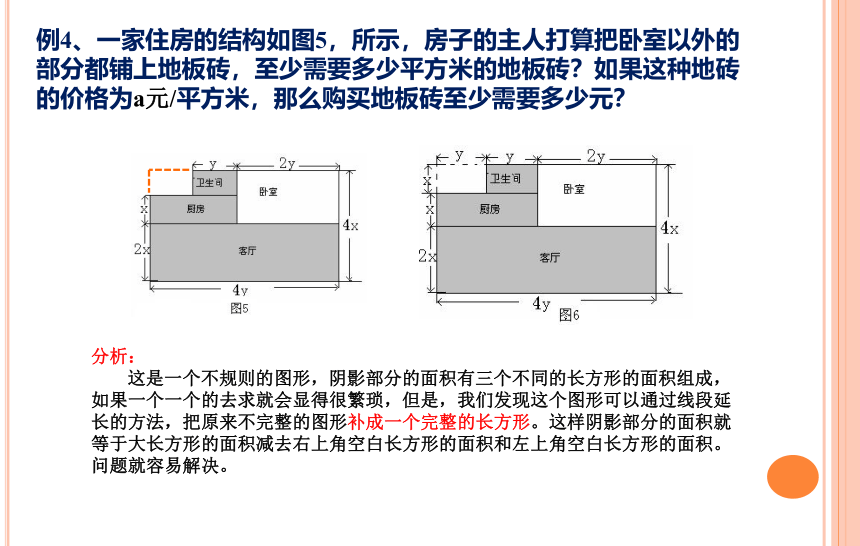
例4、一家住房的结构如图5,所示,房子的主人打算把卧室以外的部分都铺上地板砖,至少需要多少平方米的地板砖?如果这种地砖的价格为a元/平方米,那么购买地板砖至少需要多少元?
分析:
这是一个不规则的图形,阴影部分的面积有三个不同的长方形的面积组成,如果一个一个的去求就会显得很繁琐,但是,我们发现这个图形可以通过线段延长的方法,把原来不完整的图形补成一个完整的长方形。这样阴影部分的面积就等于大长方形的面积减去右上角空白长方形的面积和左上角空白长方形的面积。问题就容易解决。
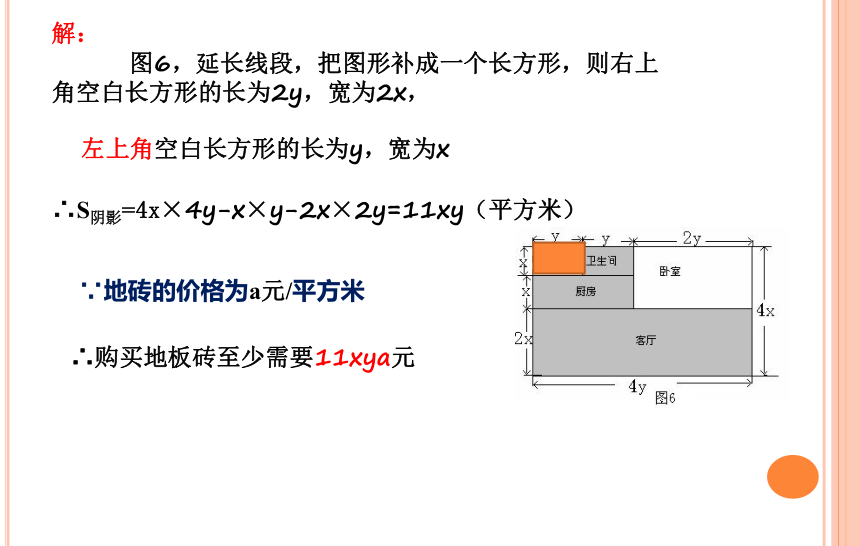
解:
图6,延长线段,把图形补成一个长方形,则右上角空白长方形的长为2y,宽为2x,
左上角空白长方形的长为y,宽为x
∴S阴影=4x×4y-x×y-2x×2y=11xy(平方米)
∴购买地板砖至少需要11xya元
∵地砖的价格为a元/平方米
2、运用分割的思想
把不规则的图形分割成几个不同或相同的规则图形。
例5、如图7,阴影部分的面积是( )
a. b.
c. d.
分析:这是一个不规则的图形,但是,我们发现这个图形可以通过线段延长的方法,把原来不完整的图形分割成两个个完整的长方形。这样阴影部分的面积就等于大长方形的面积加上小长方形的面积。问题就容易解决。
解:
延长线段,把图形分割成两个长方形
大长方形的面积为:
小长方形的面积为:
2y×1.5x=3xy
y×0.5x=0.5xy
阴影部分的面积为:
3xy+0.5 xy=3.5xy
a
3、运用平移的思想
例6、如图9,阴影部分的面积是 。
分析:这是一个不规则的图形,但是,我们发现这个图形中,上端两个小长方形的长是相同的,所以可以通过平移的方法,把这两个小长方形拼成一个完整的图形,这个图形是一个边长为2a的正方形,这样阴影部分的面积就等于长方形的面积加上正方形的面积。
解:将右上端的长方形平移到左边,得到一个边长2a的正方形
阴影部分的面积为:
(2a)2+(2a+3b)×b=4a2+2ab+3b2
4a2+2ab+3b2
4、运用恒等变形的思想
例7、如图11所示,图a,表示的是边长为a的大正方形中剪去一个边长为b的小正方形,小明将图a的阴影部分拼成了一个矩形,如图b。这一过程可以验证( )
A.a2+b2-2ab=(a-b)2 B.a2+b2+2ab=(a+b)2
C.2a2-3ab+b2=(2a-b)(a-b) D.a2-b2=(a+b) (a-b)
分析:这是一个面积恒等变形问题。图形可以有不同的表示方式,但是,图形的面积是保持不变的。
在图a中,阴影部分的面积为:a2-b2,
图b中阴影部分的面积为:(a+b)(a-b),
因为,图形的面积是保持不变,所以,a2-b2=(a+b)(a-b),
因此,这个变形图形验证的是a2-b2=(a+b)(a-b)。
D
5、运用转化的思想
例8、如图12,求阴影部分的面积
分析:仔细观察图形,知道空白长方形的长 3.5a,是个小数,为此,我们不妨采用对称的方法,把原来的图形进行加倍,这样就得到两个长为7a,宽为a的长方形和一个长为11a,宽为6a的长方形,两个面积的差的一半,就是所求阴影部分的面积。
解:整个阴影部分的面积为:
(11a×6a-7a×a×2)=26a2
图13
6、方程的思想
例9、如右图14,四个一样大的长方形和一个小的正方形拼成一个大正方形,其中大、小正方形的面积分别是64平方米和9平方米.求长方形的长、宽各是多少?
分析:真正清楚长方形的长、宽和大正方形、小正方形的边长的关系是问题解决的关键。数形结合的思想是解决问题的基础。从图形中可以看出大正方形是长方形的长与宽的和,小正方形的边长是长方形的长与宽的差。
解:设长方形的长是x米,宽是y米,
根据题意,得:
(x+y)2=64,(x-y)2=9,
∴x+y=8,x-y=3,
解得:x=
,y=
;
a
a
a
1、求下图中阴影部分的面积并计算当a=10时阴影部分面积
练习一
转化法
解:阴影部分面积
∴S阴影=a×a
=a
当a=10时
S阴影=50
a
a
a
2、求下图中阴影部分的面积
凑整法
解:
阴影部分面积=正方形面积减去2个圆的面积
∴S阴影=a -2π×(a) =a - πa
a
a
a
3、求下图中阴影部分的面积
平移法
解:
阴影部分面积=小正方形面积
∴S阴影=(a-a) = a
3a+2b
a+2b
a+b
2a+b
4、求下图中阴影部分的面积并计算当a=10,b=4时阴影部分面积
∴S阴影=(S1+S2)+(S4+S3) =2a(2a+b)+a(a+2b)=5a +4ab
S1
S4
S3
S2
分割法
1、有一张边长为a厘米的正方形桌面,因为实际需要,需将正方形边长增加b厘米,木工师傅设计了如图所示的三种方案:
小明发现这三种方案都能验证公式:a2+2ab+b2=(a+b)2,对于方案一,小明是这样验证的:
a2+ab+ab+b2=a2+2ab+b2=(a+b)2
请你根据方案二、方案三,写出公式的验证过程.
方案二:a2+ab+(a+b)b=a2+ab+ab+b2=a2+2ab+b2=(a+b)2,
方案三:a2+[a+(a+b) ]b+[a+(a+b) ]b
=a2+2ab+b2=(a+b)2.
练习二
恒等变形
2、王老师家买了一套新房,其结构如图所示(单位:米).他打算将卧室铺木地板,其余部分铺地砖.
(1)木地板和地砖分别需要多少平方米?
(2)如果地砖的价格为每平方米x元,木地板的价格为每平方米3x元,那么王老师需要花多少钱?
卫生间、厨房、客厅的面积和:
b·(4a-2a-a)+a·(4b-2b)+2a·4b
=ab+2ab+8ab
=11ab(平方米),
即木地板需要4ab平方米,地砖需要11ab平方米.
解:(1)卧室的面积是2b(4a-2a)=4ab(平方米).
(2)11ab·x+4ab·3x=11abx+12abx=23abx(元).
即王老师需要花23abx元.
3、在矩形ABCD内,将两张边长分别为a和b(a>b)的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),矩形中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为S1,图2中阴影部分的面积为S2.当AD﹣AB=2时,S2﹣S1的值为( )
解:S1=(AB﹣a) a+(CD﹣b)(AD﹣a)=(AB﹣a) a+(AB﹣b)(AD﹣a),
S2=AB(AD﹣a)+(a﹣b)(AB﹣a),
∴S2﹣S1=AB(AD﹣a)+(a﹣b)(AB﹣a)﹣(AB﹣a) a﹣(AB﹣b)(AD﹣a)
=(AD﹣a)(AB﹣AB+b)+(AB﹣a)(a﹣b﹣a)
=b AD﹣ab﹣b AB+ab
=b(AD﹣AB)
=2b.
A.2a B.2b C.2a﹣2b D.﹣2b
【分析】利用面积的和差分别表示出S1和S2,然后利用整式的混合运算计算它们的差.
B
4、如图1所示,从边长为a的正方形纸片中减去一个边长为b的小正方形,再沿着线段AB剪开,把剪成的两张纸拼成如图2的等腰梯形,
(1)设图1中阴影部分面积为S1,图2中阴影部分面积为S2,请直接用含a,b的代数式表示S1和S2;
(2)请写出上述过程所揭示的乘法公式.
S1=a -b
S2= [a+a++bb) ](a-b)
=(a+b)(a-b)
解:(1)
(2)
a -b =(a+b)(a-b)
所揭示的乘法公式:
整式中求阴影图形面积的数学思想
沪科版数学七年级下册
第八章 本章复习与测试
1、运用整体的思想
1.1
把分散的图形重新组合成整体
例1、如图1,某正方形广场的四角都有一块半径相同的四分之一圆形的草地,若圆的半径为r米,正方形的边长为a米。
(1)请用代数式表示空地的面积。
(2)若正方形的边长为300米,圆形的半径为10米,求广场空地的面积(计算结果保留π)。
分析:正方形的四个角上的四个扇形,因为它们的半径是相同的,所以,这四个分散的扇形就可以拼成一个半径为r米的整圆。这样,阴影部分的面积就等于正方形的面积减去两个圆的面积。
解:1、空地的面积为a2-πr2(平方米)
2、当a=300,r=10时,广场空地的面积为:90000-100π(平方米)
例2、如图2,四个直角三角形的直角边的长都是a,正方形的边长为a,试用整式表示阴影部分的面积。
分析:图中的四个直角三角形,通过平移、旋转等手段,就可以将四个直角三角形拼成两个边长为a 的正方形,这样阴影部分的面积就等于长方形的面积减去三个正方形的面积。
解:阴影部分的面积为:
xy-3a2
1.2
把不完整的图形补成整体
例3、如图3,根据图中的信息,求阴影部分的面积。
分析:这是一个不规则的图形,要想求出阴影部分的面积是不容易计算的。
但是,我们发现这个图形可以通过线段延长的方法,把原来不完整的图形补成一个完整的长方形。这样阴影部分的面积就等于大长方形的面积减去右上角空白长方形的面积。问题解决。
解:如图4,延长线段,把图形补成一个长方形,则空白长方形的长为b-t,宽为a-t,
S阴影=ab-(b-t)(a-t)=at+bt-t2。
例4、一家住房的结构如图5,所示,房子的主人打算把卧室以外的部分都铺上地板砖,至少需要多少平方米的地板砖?如果这种地砖的价格为a元/平方米,那么购买地板砖至少需要多少元?
分析:
这是一个不规则的图形,阴影部分的面积有三个不同的长方形的面积组成,如果一个一个的去求就会显得很繁琐,但是,我们发现这个图形可以通过线段延长的方法,把原来不完整的图形补成一个完整的长方形。这样阴影部分的面积就等于大长方形的面积减去右上角空白长方形的面积和左上角空白长方形的面积。问题就容易解决。
解:
图6,延长线段,把图形补成一个长方形,则右上角空白长方形的长为2y,宽为2x,
左上角空白长方形的长为y,宽为x
∴S阴影=4x×4y-x×y-2x×2y=11xy(平方米)
∴购买地板砖至少需要11xya元
∵地砖的价格为a元/平方米
2、运用分割的思想
把不规则的图形分割成几个不同或相同的规则图形。
例5、如图7,阴影部分的面积是( )
a. b.
c. d.
分析:这是一个不规则的图形,但是,我们发现这个图形可以通过线段延长的方法,把原来不完整的图形分割成两个个完整的长方形。这样阴影部分的面积就等于大长方形的面积加上小长方形的面积。问题就容易解决。
解:
延长线段,把图形分割成两个长方形
大长方形的面积为:
小长方形的面积为:
2y×1.5x=3xy
y×0.5x=0.5xy
阴影部分的面积为:
3xy+0.5 xy=3.5xy
a
3、运用平移的思想
例6、如图9,阴影部分的面积是 。
分析:这是一个不规则的图形,但是,我们发现这个图形中,上端两个小长方形的长是相同的,所以可以通过平移的方法,把这两个小长方形拼成一个完整的图形,这个图形是一个边长为2a的正方形,这样阴影部分的面积就等于长方形的面积加上正方形的面积。
解:将右上端的长方形平移到左边,得到一个边长2a的正方形
阴影部分的面积为:
(2a)2+(2a+3b)×b=4a2+2ab+3b2
4a2+2ab+3b2
4、运用恒等变形的思想
例7、如图11所示,图a,表示的是边长为a的大正方形中剪去一个边长为b的小正方形,小明将图a的阴影部分拼成了一个矩形,如图b。这一过程可以验证( )
A.a2+b2-2ab=(a-b)2 B.a2+b2+2ab=(a+b)2
C.2a2-3ab+b2=(2a-b)(a-b) D.a2-b2=(a+b) (a-b)
分析:这是一个面积恒等变形问题。图形可以有不同的表示方式,但是,图形的面积是保持不变的。
在图a中,阴影部分的面积为:a2-b2,
图b中阴影部分的面积为:(a+b)(a-b),
因为,图形的面积是保持不变,所以,a2-b2=(a+b)(a-b),
因此,这个变形图形验证的是a2-b2=(a+b)(a-b)。
D
5、运用转化的思想
例8、如图12,求阴影部分的面积
分析:仔细观察图形,知道空白长方形的长 3.5a,是个小数,为此,我们不妨采用对称的方法,把原来的图形进行加倍,这样就得到两个长为7a,宽为a的长方形和一个长为11a,宽为6a的长方形,两个面积的差的一半,就是所求阴影部分的面积。
解:整个阴影部分的面积为:
(11a×6a-7a×a×2)=26a2
图13
6、方程的思想
例9、如右图14,四个一样大的长方形和一个小的正方形拼成一个大正方形,其中大、小正方形的面积分别是64平方米和9平方米.求长方形的长、宽各是多少?
分析:真正清楚长方形的长、宽和大正方形、小正方形的边长的关系是问题解决的关键。数形结合的思想是解决问题的基础。从图形中可以看出大正方形是长方形的长与宽的和,小正方形的边长是长方形的长与宽的差。
解:设长方形的长是x米,宽是y米,
根据题意,得:
(x+y)2=64,(x-y)2=9,
∴x+y=8,x-y=3,
解得:x=
,y=
;
a
a
a
1、求下图中阴影部分的面积并计算当a=10时阴影部分面积
练习一
转化法
解:阴影部分面积
∴S阴影=a×a
=a
当a=10时
S阴影=50
a
a
a
2、求下图中阴影部分的面积
凑整法
解:
阴影部分面积=正方形面积减去2个圆的面积
∴S阴影=a -2π×(a) =a - πa
a
a
a
3、求下图中阴影部分的面积
平移法
解:
阴影部分面积=小正方形面积
∴S阴影=(a-a) = a
3a+2b
a+2b
a+b
2a+b
4、求下图中阴影部分的面积并计算当a=10,b=4时阴影部分面积
∴S阴影=(S1+S2)+(S4+S3) =2a(2a+b)+a(a+2b)=5a +4ab
S1
S4
S3
S2
分割法
1、有一张边长为a厘米的正方形桌面,因为实际需要,需将正方形边长增加b厘米,木工师傅设计了如图所示的三种方案:
小明发现这三种方案都能验证公式:a2+2ab+b2=(a+b)2,对于方案一,小明是这样验证的:
a2+ab+ab+b2=a2+2ab+b2=(a+b)2
请你根据方案二、方案三,写出公式的验证过程.
方案二:a2+ab+(a+b)b=a2+ab+ab+b2=a2+2ab+b2=(a+b)2,
方案三:a2+[a+(a+b) ]b+[a+(a+b) ]b
=a2+2ab+b2=(a+b)2.
练习二
恒等变形
2、王老师家买了一套新房,其结构如图所示(单位:米).他打算将卧室铺木地板,其余部分铺地砖.
(1)木地板和地砖分别需要多少平方米?
(2)如果地砖的价格为每平方米x元,木地板的价格为每平方米3x元,那么王老师需要花多少钱?
卫生间、厨房、客厅的面积和:
b·(4a-2a-a)+a·(4b-2b)+2a·4b
=ab+2ab+8ab
=11ab(平方米),
即木地板需要4ab平方米,地砖需要11ab平方米.
解:(1)卧室的面积是2b(4a-2a)=4ab(平方米).
(2)11ab·x+4ab·3x=11abx+12abx=23abx(元).
即王老师需要花23abx元.
3、在矩形ABCD内,将两张边长分别为a和b(a>b)的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),矩形中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为S1,图2中阴影部分的面积为S2.当AD﹣AB=2时,S2﹣S1的值为( )
解:S1=(AB﹣a) a+(CD﹣b)(AD﹣a)=(AB﹣a) a+(AB﹣b)(AD﹣a),
S2=AB(AD﹣a)+(a﹣b)(AB﹣a),
∴S2﹣S1=AB(AD﹣a)+(a﹣b)(AB﹣a)﹣(AB﹣a) a﹣(AB﹣b)(AD﹣a)
=(AD﹣a)(AB﹣AB+b)+(AB﹣a)(a﹣b﹣a)
=b AD﹣ab﹣b AB+ab
=b(AD﹣AB)
=2b.
A.2a B.2b C.2a﹣2b D.﹣2b
【分析】利用面积的和差分别表示出S1和S2,然后利用整式的混合运算计算它们的差.
B
4、如图1所示,从边长为a的正方形纸片中减去一个边长为b的小正方形,再沿着线段AB剪开,把剪成的两张纸拼成如图2的等腰梯形,
(1)设图1中阴影部分面积为S1,图2中阴影部分面积为S2,请直接用含a,b的代数式表示S1和S2;
(2)请写出上述过程所揭示的乘法公式.
S1=a -b
S2= [a+a++bb) ](a-b)
=(a+b)(a-b)
解:(1)
(2)
a -b =(a+b)(a-b)
所揭示的乘法公式:
