2022年普通高等学校招生全国统一考试数学试题(乙卷文科)评讲课件(共44张PPT)
文档属性
| 名称 | 2022年普通高等学校招生全国统一考试数学试题(乙卷文科)评讲课件(共44张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-17 18:08:17 | ||
图片预览








文档简介
(共44张PPT)
2022年普通高等学校招生全国统一考试
数学试题(乙卷文科)评讲课件
A
A
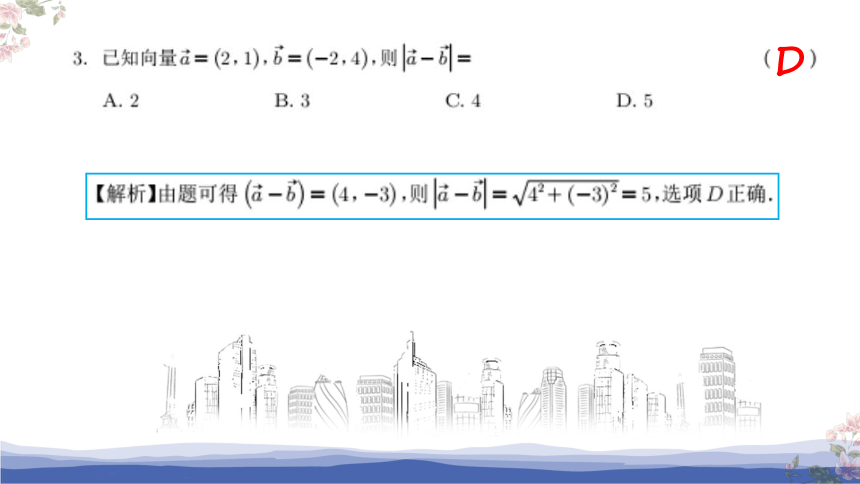
D
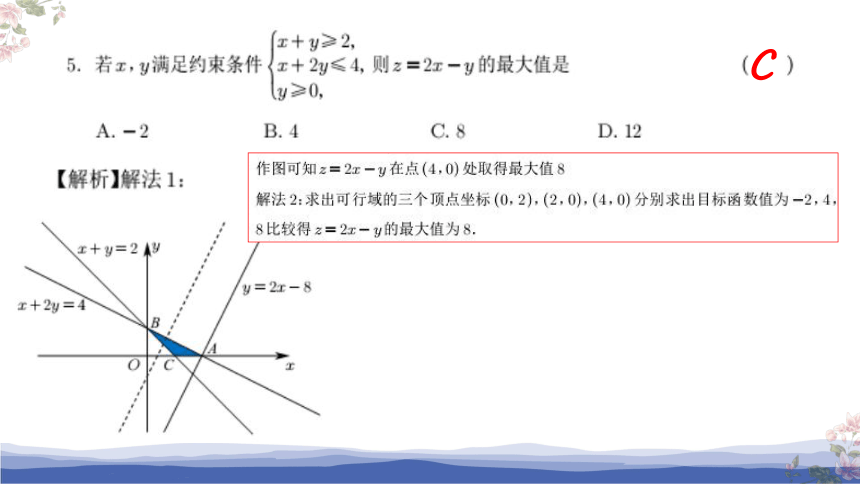
C
C
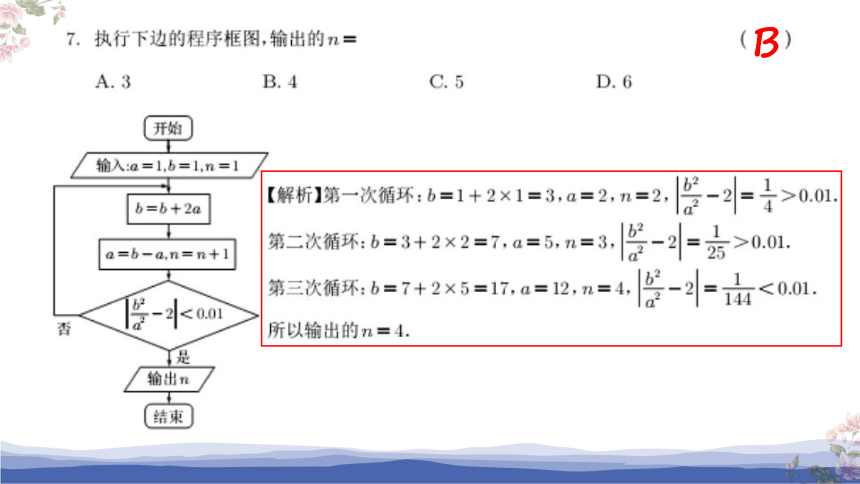
B
B
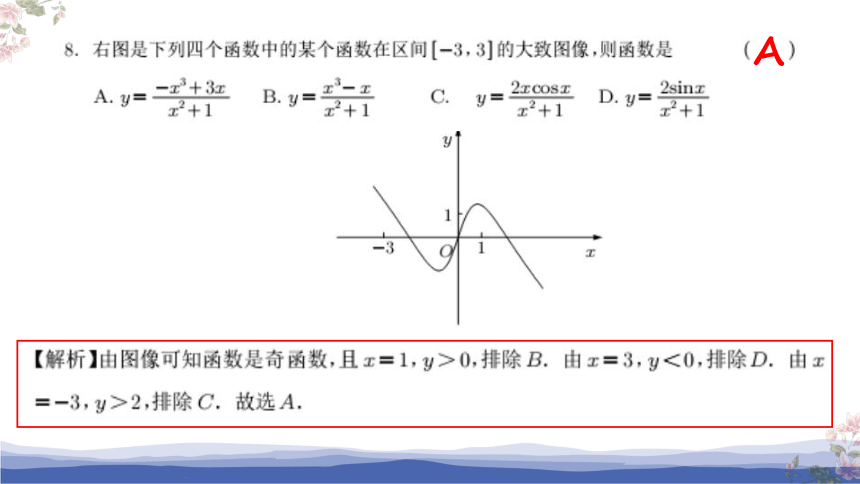
A
A
D
D
C
2
-1
未来的路,我们一起走!
可
可
同
可
O
0
6
绝密★启用前
2022年普通高等学校招生全国统一考试
(乙卷文科)
注意事项:
答题前,考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号填写在答题卡上,并
认真核准条形码上的准考证号、姓名、考场号、座位号及科目,在规定的位置贴好条形码
回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,
用橡皮擦干净后,再选涂其它答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷
上无效
考试结束后,将本试卷和答题卡一并交回.
18.(12分)
如图,四面体ABCD中,AD⊥CD,AD=CD,∠ADB=∠BDC,E为AC中点.
(1)证明:平面BED⊥平面ACD:
(2)设AB=BD=2,∠ACB=60°,点F在BD上,当△AFC面积最小时,求三棱锥F-
ABC的体积.
B
(2)由(1)可知AB=CB,又∠ACB=60°,
所以△ABC为等边三角形,则AB=CB=AC=2.
由题可知△ACD为等腰直角三角形,则AD=CD=√2.
又因为E为AC中点,所以AE=CE=DE=1,BE=√5.
如图,
F
B
连结EF,使EF⊥BD于F.作FG⊥BE于G.
因为AC⊥平面BED,EF二平面BED,FG二平面BED,
所以AC⊥EF,AC⊥FG,
此时EF为异面直线AC与BD的公垂线段,
线段EF长度即为F到AC的最短距离,即此时的△AFC面积最小.
因为FG⊥BE,FG⊥AC,BE∩AC=E,BES平面ABC,ACS平面ABC.
所以FG⊥平面ABC,线段FG长度即为三棱锥F一ABC的以△ABC为底面的高.
因为BE=5,DE=1,BD=2,DE2+BE2=BD2,所以DE⊥BE.
因为sin∠DBB=器=号,所以∠DBE=30r.
则BF=BEDBE=V5x9=号,PG=BP,sin/DBE=-号×=是
4
SaAc=AC.BE=号×2×W5=VB.
则三棱锥F-ABC的体积-=Sa·PG=××是=
4
【答案】(1)这种树木平均一颗的根部横截面积云=
10
×0.6=0.06,
平均一颗的材积量可=。×3.9=0.39:
(②)由2(6-0g-刃=言2-107=0.2474-10×006×0.30=0.0134,
10
10
10
a-P-言子-102=038-10x00=0.02:
=
10
2=2f-107=1.6158-10×0.3
=1
所以√会(-'2(-列2=0.02-0.09s=v0.0I896=896×107=1.37
×10-2=0.01377
所以r=0.0134
0.01377
=0.97
2022年普通高等学校招生全国统一考试
数学试题(乙卷文科)评讲课件
A
A
D
C
C
B
B
A
A
D
D
C
2
-1
未来的路,我们一起走!
可
可
同
可
O
0
6
绝密★启用前
2022年普通高等学校招生全国统一考试
(乙卷文科)
注意事项:
答题前,考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号填写在答题卡上,并
认真核准条形码上的准考证号、姓名、考场号、座位号及科目,在规定的位置贴好条形码
回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,
用橡皮擦干净后,再选涂其它答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷
上无效
考试结束后,将本试卷和答题卡一并交回.
18.(12分)
如图,四面体ABCD中,AD⊥CD,AD=CD,∠ADB=∠BDC,E为AC中点.
(1)证明:平面BED⊥平面ACD:
(2)设AB=BD=2,∠ACB=60°,点F在BD上,当△AFC面积最小时,求三棱锥F-
ABC的体积.
B
(2)由(1)可知AB=CB,又∠ACB=60°,
所以△ABC为等边三角形,则AB=CB=AC=2.
由题可知△ACD为等腰直角三角形,则AD=CD=√2.
又因为E为AC中点,所以AE=CE=DE=1,BE=√5.
如图,
F
B
连结EF,使EF⊥BD于F.作FG⊥BE于G.
因为AC⊥平面BED,EF二平面BED,FG二平面BED,
所以AC⊥EF,AC⊥FG,
此时EF为异面直线AC与BD的公垂线段,
线段EF长度即为F到AC的最短距离,即此时的△AFC面积最小.
因为FG⊥BE,FG⊥AC,BE∩AC=E,BES平面ABC,ACS平面ABC.
所以FG⊥平面ABC,线段FG长度即为三棱锥F一ABC的以△ABC为底面的高.
因为BE=5,DE=1,BD=2,DE2+BE2=BD2,所以DE⊥BE.
因为sin∠DBB=器=号,所以∠DBE=30r.
则BF=BEDBE=V5x9=号,PG=BP,sin/DBE=-号×=是
4
SaAc=AC.BE=号×2×W5=VB.
则三棱锥F-ABC的体积-=Sa·PG=××是=
4
【答案】(1)这种树木平均一颗的根部横截面积云=
10
×0.6=0.06,
平均一颗的材积量可=。×3.9=0.39:
(②)由2(6-0g-刃=言2-107=0.2474-10×006×0.30=0.0134,
10
10
10
a-P-言子-102=038-10x00=0.02:
=
10
2=2f-107=1.6158-10×0.3
=1
所以√会(-'2(-列2=0.02-0.09s=v0.0I896=896×107=1.37
×10-2=0.01377
所以r=0.0134
0.01377
=0.97
同课章节目录
