20.3正方形性质 课件
图片预览






文档简介
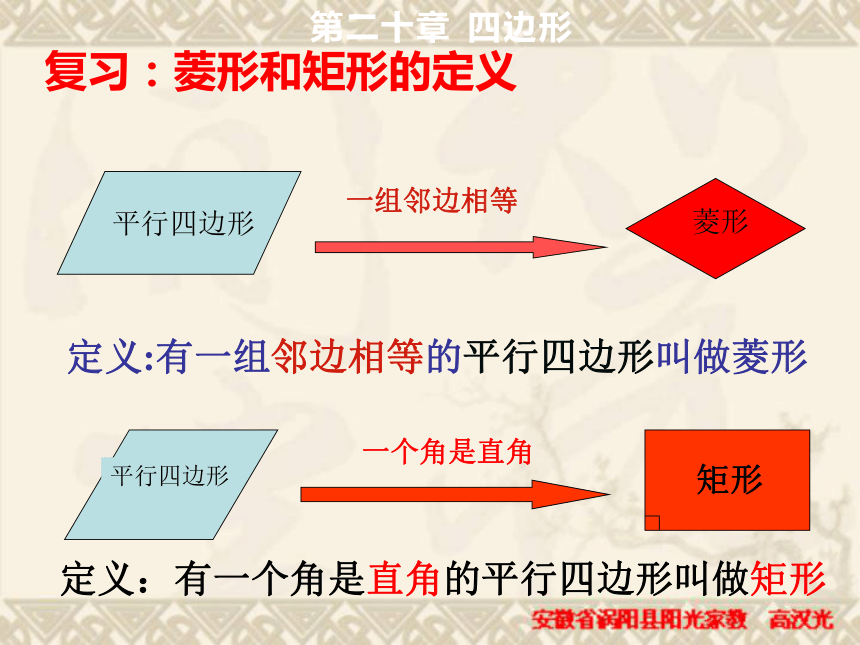
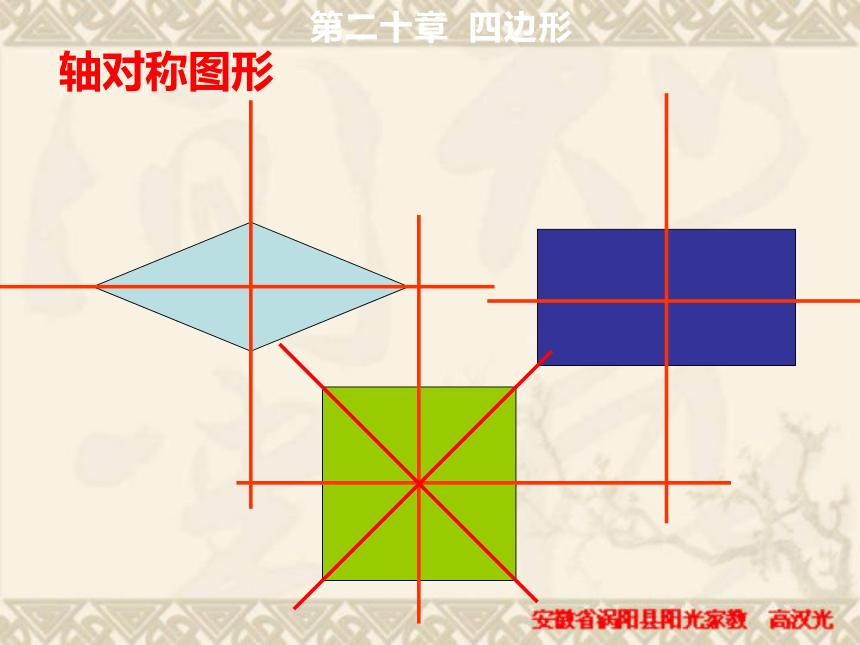
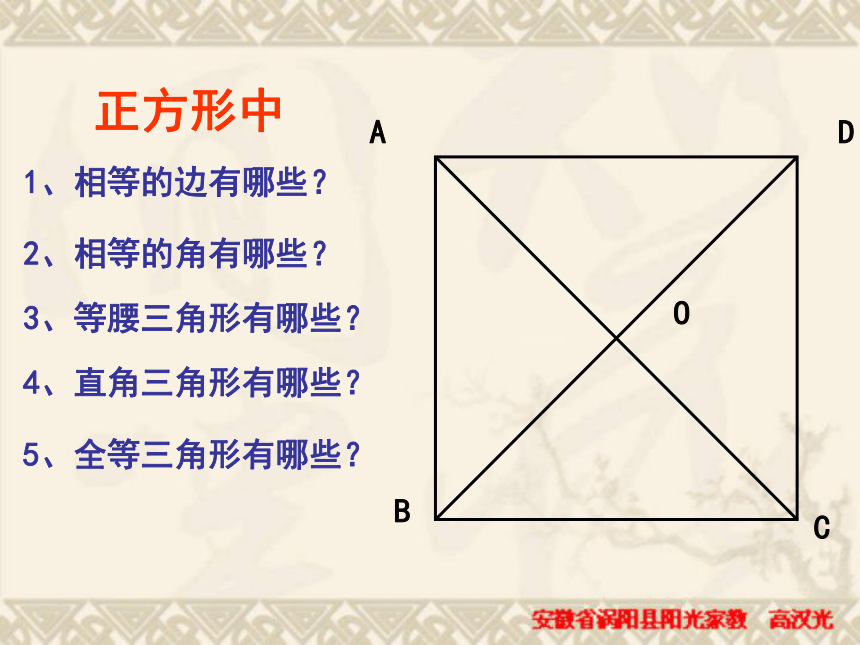
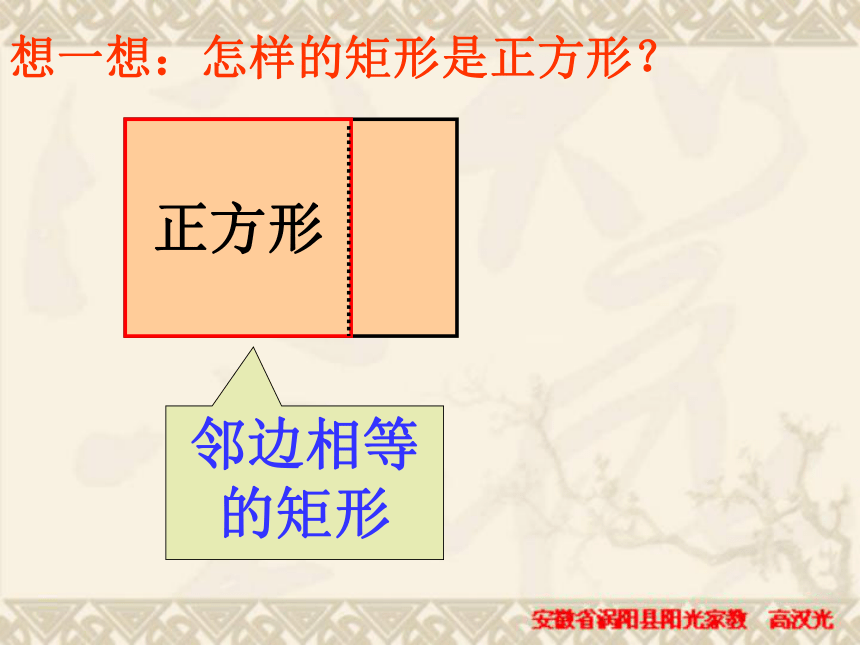
课件39张PPT。正方形2002年世界数学大会会标定义:有一组邻边相等的平行四边形叫做菱形一个角是直角定义:有一个角是直角的平行四边形叫做矩形一组邻边相等第二十章 四边形复习:菱形和矩形的定义2002年世界数学大会会标正方形的定义第二十章 四边形正方形是特殊的矩形,又是特殊的菱形,更是特殊的平行四边形,因此正方形具有这些图形的所有性质.正方形有哪些性质?把它们全部写出来,相互交流一下,看是否全面。 有一个角是直角且有一组邻边相等的平行四边形叫正方形正方形的性质边对角线对边平行四边相等对角线相等 互相垂直平分每条对角线平分一组对角四个角相等且都是直角角正方形性质正方形具有平行四边形、矩形、菱形的一切性质。轴对称图形第二十章 四边形正方形中1、相等的边有哪些?2、相等的角有哪些?3、等腰三角形有哪些?4、直角三角形有哪些?5、全等三角形有哪些?邻边相等的矩形想一想:怎样的矩形是正方形?矩形正方形 菱形正方形 一个角是直角的菱形想一想:怎样的菱形是正方形?定义:有一个角是直角且有一组邻边相等的平行四边形 叫做正方形
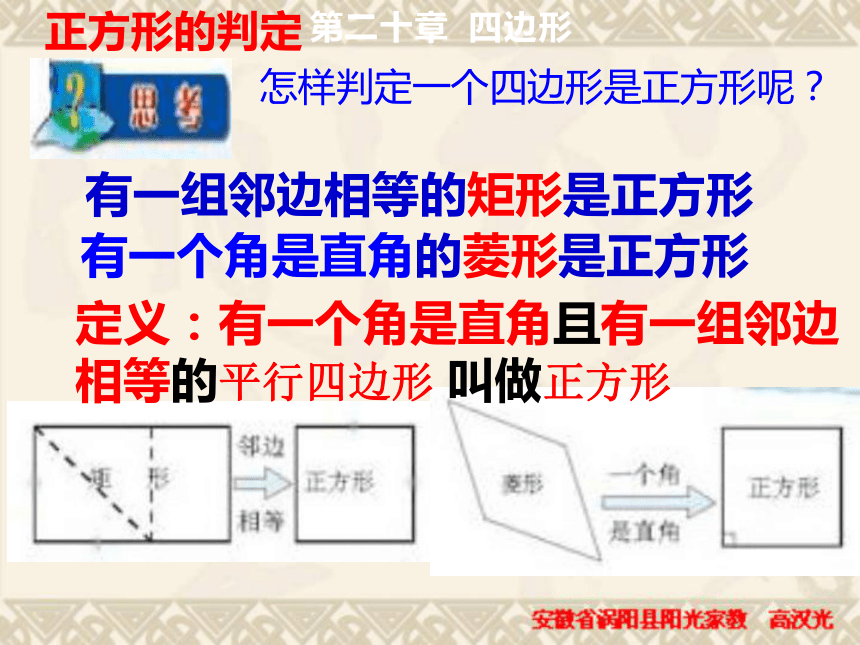
有一组邻边相等的矩形是正方形第二十章 四边形正方形的判定有一个角是直角的菱形是正方形怎样判定一个四边形是正方形呢?如何判定一个图形是正方形呢?(可从平行四边形、矩形、菱形为基础)有一组邻边相等且有一个角是直角的平行四边形叫做正方形。 定义法有一个角是直角的菱形是正方形。有一组邻边相等的矩形是正方形。正方形具有而矩形不一定具有的性质是( )
A、四个角相等.
B、对角线互相垂直.
C、对角互补.
D、对角线相等.选一选2.正方形具有而菱形不一定具有的性质( )
A、四条边相等.
B、对角线互相垂直.
C、对角线平分一组对角.
D、对角线相等. BD 下列说法对吗?
(1)四个角都相等的四边形是正方形
(2)四条边都相等的四边形是正方形
(3)四边相等,有一角是直角的四边形是正方形
(4) 正方形的一条对角线把正方形分成两个全等的等腰 直角三角形
(5) 正方形是轴对称图形,一共有2条对称轴辨一辨 在一块正方形的花坛上,欲修建两条直的小路,使得两条直的小路将花坛平均分成面积相等的四部分(不考虑道路的宽度),你有几种方法?(至少说出三种)
第二十章 四边形图案设计例1: 如图,点A'B'C'D'分别是正方形ABCD四条边上的点,并且AA'=BB'=CC'=DD'.
求证:四边形ABCD是正方形.分析(1)正方形的性质.
(2)直角三角形全等的判定.
(3)正方形的判定.
关键:如何判定四边形ABCD是正方形? 证明:∵四边形ABCD是正方形,∴AB=BC=CD=DA.
又∵AA′=BB′=CC′=DD′,
∴D′A=A′B=B′C=C′D .∵∠A=∠B=∠C=∠D=90°
∴△AA′D′≌△BB′A′≌△CC′B′≌DD′C′∴A′B′=B′C′=C′D′=D′A′.
∴四边形A′B′C′D′是菱形.又∵∠1=∠3,∠1+∠2=90°,
∴∠2+∠3=90°,∴∠D′A′B′=90°.
∴四边形A′B′C′D′是正方形. 例2.如图(3),正方形ABCD中,AC、BD相交于O,
分析:要证明BM=CN,大家观察
图形可以考虑证哪两个三角形全等 ?
MN∥AB且MN分别交OA、OB于M、N,求证:BM=CN。
你能完成证明吗???
AB=BC,∠1=∠2=45 ° 还需要的条件是 AM=BN
△ABM≌△BCN
你所要证明的两个三角形已经满足
了哪些条件?
由正方形可以得到的条件有: 例2.如图(3),正方形ABCD中,AC、BD相交于O,MN∥AB且MN分别交OA、OB于M、N,求证:BM=CN。 证明:
∵四边形ABCD是正方形 ∴OA=OB ,
∠1=∠2=∠3=45° 又∵MN∥AB
∴∠OMN=∠1=∠3=∠ONM=45° ∴OM=ON ∴OA-OM=OB-ON 即AM=BN 下面大家自己完成证明例3.已知:如图(4)在正方形ABCD中,F为CD延长线
上一点,CE⊥AF于E,交AD于M,
求证:∠MFD=45° 分析:
欲证∠MFD=45°,由于
△MDF是直角三角形,只须证△MDF是等腰三角形,即只要证 _____=_____要证MD=FD,大家只须证得哪两个三角形全等?
△CMD≌△ADF例3.已知:如图(4)在正方形ABCD中,F为CD延长线上一点,CE⊥AF于E,交AD于M, 求证:∠MFD=45° 证明:
∵CE⊥AF ∴∠ADC=∠AEM=90° 又∵∠CMD=∠AME ∴∠1=∠2 又∵CD=AD,∠ADF=∠MDC ∴Rt△CDM≌Rt△ADF (AAS) ∴DM=DF
下面的证明请大家完成
例4.如图(6)△ABC的外面作正方形ABDE和ACFG,连结BG、CE,交点为N。 求证:∠CEA=∠ABG 分析:欲证∠CEA=∠ABG,
大家想一想证明两个角相等的方法,
你有办法了吗???通过自己的努力,看能不能解决问题?
证明:∵四边形ABDE和四边形ACFG是正方形。 ∴AE=AB AG=AC ∠1=∠2=90° 又∵∠EAC=∠1+∠BAC=90°+∠BAC ∠BAG=∠2+∠BAC=90°+∠BAC ∴∠EAC=∠BAG ∴△AEC≌△ABG (SAS)
∴∠CEA=∠ABG 例5.如图四边形ABCD和DEFG都是正方形,
试说明AE=CG解:因为四边形ABCD是正方形根据正方形的四边相等,得AD=CD又知四边形DEFG也是正方形所以 DE=DG又因为正方形的每个内角为90°所以∠ADE+∠EDC=∠CDG+∠EDC所以∠ADE=∠CDG所以三角形ADE可以看成是由三角形CDG绕着点D顺时针
旋转 90° 得到。⊿AED≌ ⊿CGD所以AE=CG例6.已知:如图,△ABC中.∠ABC=90°,BD是角平分线,DE⊥AB,DF⊥BC,垂足分别是E、F.求证:四边形DEBF是正方形.证明:∵ DF⊥BC,DE⊥AB,∴ ∠DEB= ∠DFB=90°,而∠ABC=90°, ∴四边形DEBF是矩形( ), ∵ BD平分∠ABC, DF⊥BC , DE⊥AB, ∴ DE= DF( ), ∴四边形DEBF是正方形( ). 有三个角是 直角的四边形是矩形角平分线的定理有一组邻边相等的矩形是正方形例7:如图所示,正方形ABCD中,P为BD上一点,PE⊥BC于E, PF⊥DC于F。试说明:AP=EF解:连接PC∵PE⊥BC , PF⊥DC而四边形ABCD是正方形∴∠FCE=90°∴四边形PECF是矩形∴PC=EF又∵四边形BAPC是以BD为轴的轴对称图形∴AP=PC∴AP=EF 练习1.
已知:正方形ABCD对角线AC、BD相 交于点O,且AB=acm,如图(2)。
求:AC的长及正方形的面积S。 练习2.
已知:在正方形ABCD中,对角线AC、
BD相交于点O,且AC=6 cm,如图
求:正方形的面积S。
1.在正方形ABCD中,AC是对角线,AE平分∠BAC,试猜想AB、AC、BE之间的关系,并证明你的猜想.试一试2.在正方形ABCD中,对角线AC、BD相交于点O,点Q是CD上任意一点,DP⊥AQ交BC于点P.⑴求证:DQ=CP;⑵OP与OQ有何关系?试证明你的结论.3.如图,以△ABC的边AB、AC向形外作正方形ABDE和ACFG,M是BC的中点.求证:
⑴CE=BG;
⑵EG=2AM.MEDFGBCA4.求证:矩形的四个角的平分线所围成的四边形是正方形.5.如图,在正方形ABCD中,E在BC的延长线上,且CE=AC,AE交CD于F,则求∠AFC的度数6.如图(5),在AB上取一点C,以AC、BC为正方形的一边在同一侧作正方形AEDC和BCFG连结AF、BD延长BD交AF于H。 求证:(1) △ACF≌△DCB
(2) BH⊥AF
证明:
7.如图,点E、F在正方形ABCD的边BC、CD上,BE=CF.
(1)AE与BF相等吗?为什么?
(2)AE与BF是否垂直?说明你的理由。 8.如图正方形ABCD的边长为1,E、F分别为BC、CD上的点,若BE+DF=EF,
求证:∠EAF=450G小结: 正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形。?正方形的性质= 正方形性质:
边: 对边平行
四边相等
角 :四个角都是直角 对角线:相等
互相垂直平分
每条对角线平分一组对角。
正方形的四个角都是直角,四条边相等.
正方形的对角线相等,并且互相垂直平分,每条对角线平分一组对角.有一组邻边相等有一个角是直角有一个角是直角有一组邻边相等有一组邻边相等有一个角是直角有一组邻边相等且有一个角是直角第二十章 四边形各平行四边形关系再认识平行四边形矩形菱形正
方
形平行四边形、矩形、菱形、正方形的关系回顾平行四边形,矩形,菱形的性质,完成表格前三列对边平行且相等四条边相等对边平行且四条边相等对角相等四个角都是直角四个角都是直角对角线互相平分对角线相等对角线互相垂直,每条对角线平分一组对角对角线相等且互相垂直平分,每条对角线平分一组对角中心对称图形既是中心对称图形又是轴对称图形既是中心对称图形又是轴对称图形既是中心对称图形又是轴对称图形图形性质分类正方形类
比
归
纳
有一组邻边相等的矩形是正方形第二十章 四边形正方形的判定有一个角是直角的菱形是正方形怎样判定一个四边形是正方形呢?如何判定一个图形是正方形呢?(可从平行四边形、矩形、菱形为基础)有一组邻边相等且有一个角是直角的平行四边形叫做正方形。 定义法有一个角是直角的菱形是正方形。有一组邻边相等的矩形是正方形。正方形具有而矩形不一定具有的性质是( )
A、四个角相等.
B、对角线互相垂直.
C、对角互补.
D、对角线相等.选一选2.正方形具有而菱形不一定具有的性质( )
A、四条边相等.
B、对角线互相垂直.
C、对角线平分一组对角.
D、对角线相等. BD 下列说法对吗?
(1)四个角都相等的四边形是正方形
(2)四条边都相等的四边形是正方形
(3)四边相等,有一角是直角的四边形是正方形
(4) 正方形的一条对角线把正方形分成两个全等的等腰 直角三角形
(5) 正方形是轴对称图形,一共有2条对称轴辨一辨 在一块正方形的花坛上,欲修建两条直的小路,使得两条直的小路将花坛平均分成面积相等的四部分(不考虑道路的宽度),你有几种方法?(至少说出三种)
第二十章 四边形图案设计例1: 如图,点A'B'C'D'分别是正方形ABCD四条边上的点,并且AA'=BB'=CC'=DD'.
求证:四边形ABCD是正方形.分析(1)正方形的性质.
(2)直角三角形全等的判定.
(3)正方形的判定.
关键:如何判定四边形ABCD是正方形? 证明:∵四边形ABCD是正方形,∴AB=BC=CD=DA.
又∵AA′=BB′=CC′=DD′,
∴D′A=A′B=B′C=C′D .∵∠A=∠B=∠C=∠D=90°
∴△AA′D′≌△BB′A′≌△CC′B′≌DD′C′∴A′B′=B′C′=C′D′=D′A′.
∴四边形A′B′C′D′是菱形.又∵∠1=∠3,∠1+∠2=90°,
∴∠2+∠3=90°,∴∠D′A′B′=90°.
∴四边形A′B′C′D′是正方形. 例2.如图(3),正方形ABCD中,AC、BD相交于O,
分析:要证明BM=CN,大家观察
图形可以考虑证哪两个三角形全等 ?
MN∥AB且MN分别交OA、OB于M、N,求证:BM=CN。
你能完成证明吗???
AB=BC,∠1=∠2=45 ° 还需要的条件是 AM=BN
△ABM≌△BCN
你所要证明的两个三角形已经满足
了哪些条件?
由正方形可以得到的条件有: 例2.如图(3),正方形ABCD中,AC、BD相交于O,MN∥AB且MN分别交OA、OB于M、N,求证:BM=CN。 证明:
∵四边形ABCD是正方形 ∴OA=OB ,
∠1=∠2=∠3=45° 又∵MN∥AB
∴∠OMN=∠1=∠3=∠ONM=45° ∴OM=ON ∴OA-OM=OB-ON 即AM=BN 下面大家自己完成证明例3.已知:如图(4)在正方形ABCD中,F为CD延长线
上一点,CE⊥AF于E,交AD于M,
求证:∠MFD=45° 分析:
欲证∠MFD=45°,由于
△MDF是直角三角形,只须证△MDF是等腰三角形,即只要证 _____=_____要证MD=FD,大家只须证得哪两个三角形全等?
△CMD≌△ADF例3.已知:如图(4)在正方形ABCD中,F为CD延长线上一点,CE⊥AF于E,交AD于M, 求证:∠MFD=45° 证明:
∵CE⊥AF ∴∠ADC=∠AEM=90° 又∵∠CMD=∠AME ∴∠1=∠2 又∵CD=AD,∠ADF=∠MDC ∴Rt△CDM≌Rt△ADF (AAS) ∴DM=DF
下面的证明请大家完成
例4.如图(6)△ABC的外面作正方形ABDE和ACFG,连结BG、CE,交点为N。 求证:∠CEA=∠ABG 分析:欲证∠CEA=∠ABG,
大家想一想证明两个角相等的方法,
你有办法了吗???通过自己的努力,看能不能解决问题?
证明:∵四边形ABDE和四边形ACFG是正方形。 ∴AE=AB AG=AC ∠1=∠2=90° 又∵∠EAC=∠1+∠BAC=90°+∠BAC ∠BAG=∠2+∠BAC=90°+∠BAC ∴∠EAC=∠BAG ∴△AEC≌△ABG (SAS)
∴∠CEA=∠ABG 例5.如图四边形ABCD和DEFG都是正方形,
试说明AE=CG解:因为四边形ABCD是正方形根据正方形的四边相等,得AD=CD又知四边形DEFG也是正方形所以 DE=DG又因为正方形的每个内角为90°所以∠ADE+∠EDC=∠CDG+∠EDC所以∠ADE=∠CDG所以三角形ADE可以看成是由三角形CDG绕着点D顺时针
旋转 90° 得到。⊿AED≌ ⊿CGD所以AE=CG例6.已知:如图,△ABC中.∠ABC=90°,BD是角平分线,DE⊥AB,DF⊥BC,垂足分别是E、F.求证:四边形DEBF是正方形.证明:∵ DF⊥BC,DE⊥AB,∴ ∠DEB= ∠DFB=90°,而∠ABC=90°, ∴四边形DEBF是矩形( ), ∵ BD平分∠ABC, DF⊥BC , DE⊥AB, ∴ DE= DF( ), ∴四边形DEBF是正方形( ). 有三个角是 直角的四边形是矩形角平分线的定理有一组邻边相等的矩形是正方形例7:如图所示,正方形ABCD中,P为BD上一点,PE⊥BC于E, PF⊥DC于F。试说明:AP=EF解:连接PC∵PE⊥BC , PF⊥DC而四边形ABCD是正方形∴∠FCE=90°∴四边形PECF是矩形∴PC=EF又∵四边形BAPC是以BD为轴的轴对称图形∴AP=PC∴AP=EF 练习1.
已知:正方形ABCD对角线AC、BD相 交于点O,且AB=acm,如图(2)。
求:AC的长及正方形的面积S。 练习2.
已知:在正方形ABCD中,对角线AC、
BD相交于点O,且AC=6 cm,如图
求:正方形的面积S。
1.在正方形ABCD中,AC是对角线,AE平分∠BAC,试猜想AB、AC、BE之间的关系,并证明你的猜想.试一试2.在正方形ABCD中,对角线AC、BD相交于点O,点Q是CD上任意一点,DP⊥AQ交BC于点P.⑴求证:DQ=CP;⑵OP与OQ有何关系?试证明你的结论.3.如图,以△ABC的边AB、AC向形外作正方形ABDE和ACFG,M是BC的中点.求证:
⑴CE=BG;
⑵EG=2AM.MEDFGBCA4.求证:矩形的四个角的平分线所围成的四边形是正方形.5.如图,在正方形ABCD中,E在BC的延长线上,且CE=AC,AE交CD于F,则求∠AFC的度数6.如图(5),在AB上取一点C,以AC、BC为正方形的一边在同一侧作正方形AEDC和BCFG连结AF、BD延长BD交AF于H。 求证:(1) △ACF≌△DCB
(2) BH⊥AF
证明:
7.如图,点E、F在正方形ABCD的边BC、CD上,BE=CF.
(1)AE与BF相等吗?为什么?
(2)AE与BF是否垂直?说明你的理由。 8.如图正方形ABCD的边长为1,E、F分别为BC、CD上的点,若BE+DF=EF,
求证:∠EAF=450G小结: 正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形。?正方形的性质= 正方形性质:
边: 对边平行
四边相等
角 :四个角都是直角 对角线:相等
互相垂直平分
每条对角线平分一组对角。
正方形的四个角都是直角,四条边相等.
正方形的对角线相等,并且互相垂直平分,每条对角线平分一组对角.有一组邻边相等有一个角是直角有一个角是直角有一组邻边相等有一组邻边相等有一个角是直角有一组邻边相等且有一个角是直角第二十章 四边形各平行四边形关系再认识平行四边形矩形菱形正
方
形平行四边形、矩形、菱形、正方形的关系回顾平行四边形,矩形,菱形的性质,完成表格前三列对边平行且相等四条边相等对边平行且四条边相等对角相等四个角都是直角四个角都是直角对角线互相平分对角线相等对角线互相垂直,每条对角线平分一组对角对角线相等且互相垂直平分,每条对角线平分一组对角中心对称图形既是中心对称图形又是轴对称图形既是中心对称图形又是轴对称图形既是中心对称图形又是轴对称图形图形性质分类正方形类
比
归
纳
