沪科版数学七年级下册 10.3 平行线的性质导学案(无答案)
文档属性
| 名称 | 沪科版数学七年级下册 10.3 平行线的性质导学案(无答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 312.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-17 08:11:24 | ||
图片预览

文档简介
第10章 相交线、平行线与平移
10.3平行线的性质
【教学目标】
知识与技能
1.探索并掌握平行线的性质,能用平行线性质进行简单的推理和计算.
2.能区分平行线的性质和判定,平行线的性质与判定的综合运用.
过程与方法
通过本节课的教学,培养学生的概括能力和“观察-猜想-证明”的探索方法,培养学生的辩证思维能力和逻辑思维能力.
情感、态度与价值观
1.通过推理论证教学,培养学生的分析问题和解决问题的能力.
2.培养学生的主体意识,向学生渗透讨论的数学思想,培养学生思维的灵活性和广阔性.
【教学重难点】
重点: 平行线性质的研究和发现过程;用平行线性质进行简单的推理和计算.
难点: 正确区分平行线的性质和判定.
【导学过程】
【知识回顾】
1、平行线的判定方法有哪些?
(1) (2) (3)
2、填空:如图
(1)由∠1=∠2,可以得到 ∥ ,理由是
(2)由∠3=∠4,可以得到 ∥ ,理由是
(3)由∠DAB=∠5,可以得到 ∥ ,理由是
(4)由∠DAB+∠CDA,可以得到 ∥ ,理由是
【新知探究】
1、操作:画直线AB∥CD,再画一条直线EF分别与AB、CD相交得8个角,标出所形成的八个角,如图所示.
2、观察并猜想:
(1)∠1和∠5是 角,数量关系是:
(2)∠3和∠5是 角,数量关系是:
(3)∠3和∠6是 角,数量关系是:
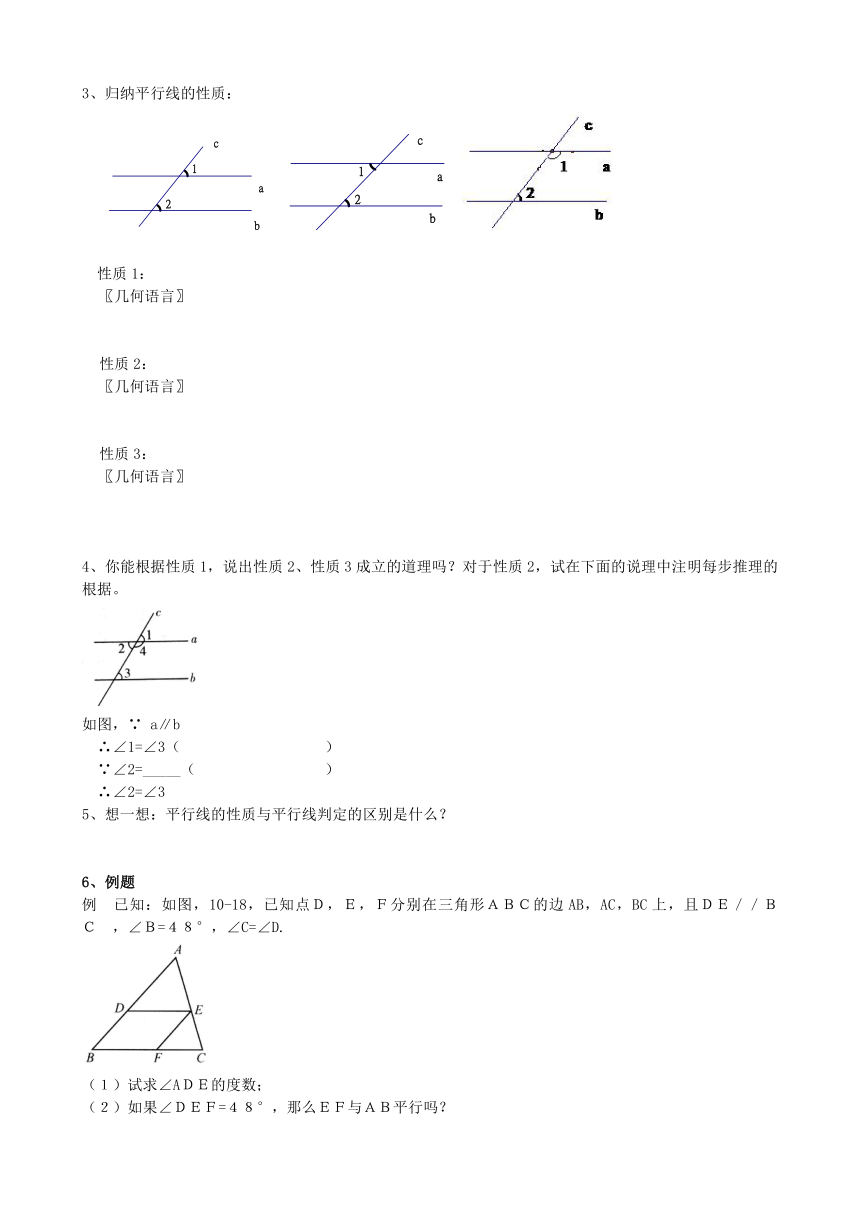
3、归纳平行线的性质:
性质1:
〖几何语言〗
性质2:
〖几何语言〗
性质3:
〖几何语言〗
4、你能根据性质1,说出性质2、性质3成立的道理吗?对于性质2,试在下面的说理中注明每步推理的根据。
如图,∵ a∥b
∴∠1=∠3( )
∵∠2=_____( )
∴∠2=∠3
5、想一想:平行线的性质与平行线判定的区别是什么?
6、例题
例 已知:如图,10-18,已知点D,E,F分别在三角形ABC的边AB,AC,BC上,且DE//BC ,∠B=48°,∠C=∠D.
(1)试求∠ADE的度数;
(2)如果∠DEF=48°,那么EF与AB平行吗?
【随堂练习】
1. 看图填空:
(1)由DE∥BC,可以得到∠ADE=________,
依据是_____________________________________;
(2)由DE∥BC,可以得到∠DFB=________,依据是__________________;
(3)由DE∥BC,可以得到∠C+________=180°,依据__________________;
(4)由DF∥AC,可以得到∠AED=________,依据_____________________;
(5)由DF∥AC,可以得到∠C=________,依据是____________________;
2.如图AB∥EF,DE∥BC,且∠E=120°,那么你能求出∠1、∠2、∠B的度数吗?为什么?
3.如图,在甲、乙两地之间要修一条笔直的公路,从甲地测得公路的走向是北偏东42°,如果甲、乙两地同时开工,若干天后公路能准确接通,乙地所修公路的走向应怎样?
4.如图,直线a∥b,直线c与a,b相交,∠1=70°,求∠2的度数。
5.如图,已知DE∥BC,BE平分∠DBC,∠D=110°,求∠E的度数。
6.已知,如图,AD∥BE,DE∥AB,试说明∠A=∠E。
7. 如图是举世闻名的三星堆考古发掘出的一个梯形残缺玉片,工作人员从玉片上已经量得∠A=115°,
∠D=110°。已知梯形的两底AD∥BC,请你求出另外两个角的度数,并说明理由。
【知识梳理】
本节课你学到了什么?有什么收获和体会?还有什么困惑?
1.______叫两直线平行。
2.同位角______两直线平行,两直线_____同位角相等。
3.内错角_____两直线平行,两直线_____内错角相等。
4.同 内角_____两直线平行,两直线_____同 内角平行。
5.平行线的性质和判定方法的关系是_______________。
10.3平行线的性质
【教学目标】
知识与技能
1.探索并掌握平行线的性质,能用平行线性质进行简单的推理和计算.
2.能区分平行线的性质和判定,平行线的性质与判定的综合运用.
过程与方法
通过本节课的教学,培养学生的概括能力和“观察-猜想-证明”的探索方法,培养学生的辩证思维能力和逻辑思维能力.
情感、态度与价值观
1.通过推理论证教学,培养学生的分析问题和解决问题的能力.
2.培养学生的主体意识,向学生渗透讨论的数学思想,培养学生思维的灵活性和广阔性.
【教学重难点】
重点: 平行线性质的研究和发现过程;用平行线性质进行简单的推理和计算.
难点: 正确区分平行线的性质和判定.
【导学过程】
【知识回顾】
1、平行线的判定方法有哪些?
(1) (2) (3)
2、填空:如图
(1)由∠1=∠2,可以得到 ∥ ,理由是
(2)由∠3=∠4,可以得到 ∥ ,理由是
(3)由∠DAB=∠5,可以得到 ∥ ,理由是
(4)由∠DAB+∠CDA,可以得到 ∥ ,理由是
【新知探究】
1、操作:画直线AB∥CD,再画一条直线EF分别与AB、CD相交得8个角,标出所形成的八个角,如图所示.
2、观察并猜想:
(1)∠1和∠5是 角,数量关系是:
(2)∠3和∠5是 角,数量关系是:
(3)∠3和∠6是 角,数量关系是:
3、归纳平行线的性质:
性质1:
〖几何语言〗
性质2:
〖几何语言〗
性质3:
〖几何语言〗
4、你能根据性质1,说出性质2、性质3成立的道理吗?对于性质2,试在下面的说理中注明每步推理的根据。
如图,∵ a∥b
∴∠1=∠3( )
∵∠2=_____( )
∴∠2=∠3
5、想一想:平行线的性质与平行线判定的区别是什么?
6、例题
例 已知:如图,10-18,已知点D,E,F分别在三角形ABC的边AB,AC,BC上,且DE//BC ,∠B=48°,∠C=∠D.
(1)试求∠ADE的度数;
(2)如果∠DEF=48°,那么EF与AB平行吗?
【随堂练习】
1. 看图填空:
(1)由DE∥BC,可以得到∠ADE=________,
依据是_____________________________________;
(2)由DE∥BC,可以得到∠DFB=________,依据是__________________;
(3)由DE∥BC,可以得到∠C+________=180°,依据__________________;
(4)由DF∥AC,可以得到∠AED=________,依据_____________________;
(5)由DF∥AC,可以得到∠C=________,依据是____________________;
2.如图AB∥EF,DE∥BC,且∠E=120°,那么你能求出∠1、∠2、∠B的度数吗?为什么?
3.如图,在甲、乙两地之间要修一条笔直的公路,从甲地测得公路的走向是北偏东42°,如果甲、乙两地同时开工,若干天后公路能准确接通,乙地所修公路的走向应怎样?
4.如图,直线a∥b,直线c与a,b相交,∠1=70°,求∠2的度数。
5.如图,已知DE∥BC,BE平分∠DBC,∠D=110°,求∠E的度数。
6.已知,如图,AD∥BE,DE∥AB,试说明∠A=∠E。
7. 如图是举世闻名的三星堆考古发掘出的一个梯形残缺玉片,工作人员从玉片上已经量得∠A=115°,
∠D=110°。已知梯形的两底AD∥BC,请你求出另外两个角的度数,并说明理由。
【知识梳理】
本节课你学到了什么?有什么收获和体会?还有什么困惑?
1.______叫两直线平行。
2.同位角______两直线平行,两直线_____同位角相等。
3.内错角_____两直线平行,两直线_____内错角相等。
4.同 内角_____两直线平行,两直线_____同 内角平行。
5.平行线的性质和判定方法的关系是_______________。
