小学数学苏教版五年级下“圆”说数学——圆的整理与复习课件(共16张PPT)
文档属性
| 名称 | 小学数学苏教版五年级下“圆”说数学——圆的整理与复习课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 42.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-16 00:00:00 | ||
图片预览



文档简介
(共16张PPT)
圆的整理与复习
苏教版义务教育教科书 数学 五年级下册
课前准备
02
橡皮
01
铅笔
03
尺子
04
自备本
o
r
d
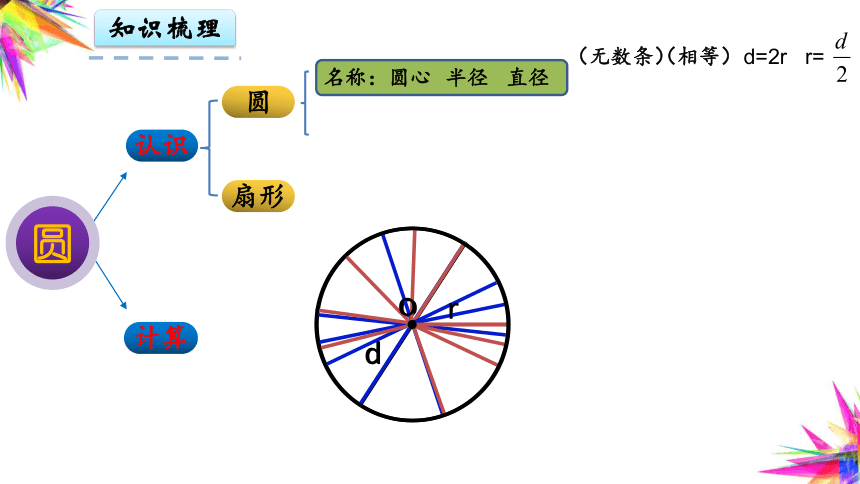
知识梳理
认识
计算
圆
圆
扇形
名称:
圆心
半径
直径
(无数条)
d=2r r=
(相等)
o
r
d
知识梳理
认识
计算
圆
圆
扇形
名称:
圆心
半径
直径
(无数条)
d=2r r=
(相等)
(轴对称图形 无数条对称轴)
o
r
d
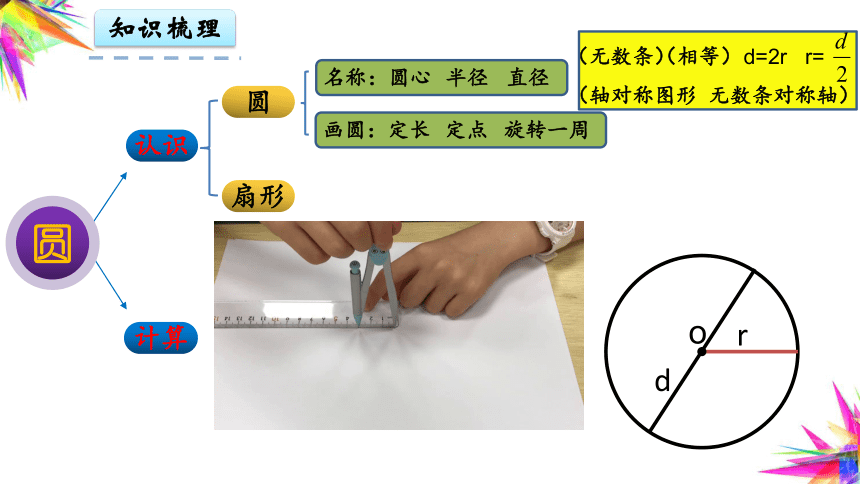
画圆:
知识梳理
认识
计算
圆
圆
扇形
名称:
圆心
半径
直径
(无数条)
d=2r r=
(相等)
(轴对称图形 无数条对称轴)
o
r
d
画圆:
定长
定点
旋转一周
知识梳理
认识
计算
圆
圆
扇形
周长
面积
名称:
圆心
半径
直径
画圆:
定长
定点
旋转一周
名称:
弧
圆心角
圆周率(π取近似值3.14)
公式:C=πd C=2πr
组合图形的面积
公式:S=πr
(无数条)
d=2r r=
(相等)
(轴对称图形 无数条对称轴)
同一圆中,圆心角决定扇形的大小。
o
r
d
1
扇形是圆的一部分。
知识梳理
r
S
d
C
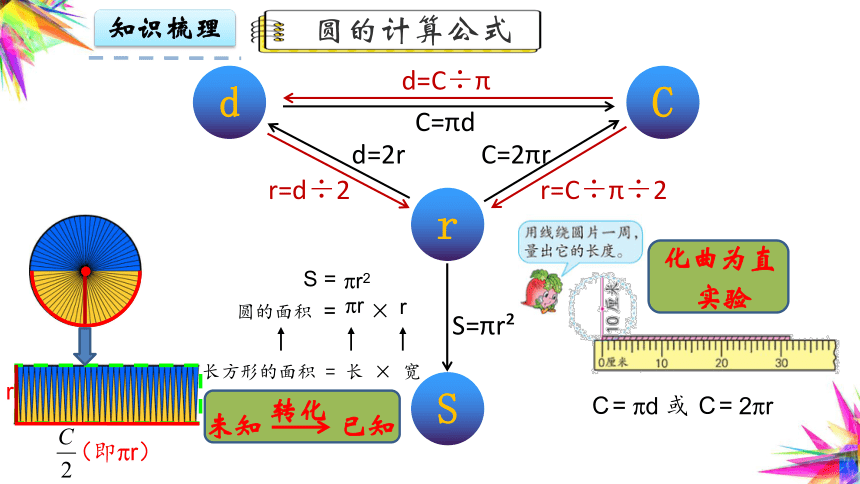
d=C÷π
r=d÷2
r=C÷π÷2
C=πd
C=2πr
d=2r
S=πr
圆的计算公式
长方形的面积 = 长 × 宽
=
×
πr2
πr
r
圆的面积
=
S
r
(即πr)
转化
πd 或
=
C
2πr
=
C
化曲为直
实验
未知
已知
典型例题
1. 下图是一个直径是20米的圆形花坛,结合圆的有关知识以及生活实际,
展开想象的翅膀,你能提出哪些数学问题?
(2)圆的周长:
π×20 = 20π(m)
C = πd
(3)圆的面积:
答:花坛的周长是20π米。
(3)花坛的面积是多少平方米?
(2)花坛的周长是多少米?
(1)花坛的半径是多少米?
(1)圆的半径:
20÷2 = 10(m)
r = d÷2
答:花坛的半径是10米。
20÷2 = 10(m)
r = d÷2
S = πr
π×10 = 100π(m )
答:花坛的占地面积是100π平方米。
r
2. 圆圆想在花坛中用篱笆围一块直径是20米的半圆形菜地。
(1)一共需要篱笆多少米?
(2)这块菜地的占地面积是多少平方米?
(1)半圆的周长:
20×3.14÷2 + 20
C半圆 = C圆÷2
(2)半圆的面积:
20÷2 = 10(m)
S半圆 = S圆÷2
π×10 ÷2
+ d
=31.4 + 20
=51.4 (m)
= 100π÷2
= 50π(m )
答:一共需要篱笆51.4米。
答:这块菜地的占地面积是50π平方米。
典型例题
S半圆 = ÷2
S圆
+ d
C半圆 = ÷2
C圆
典型例题
3. 墩墩想在直径20米的圆形花坛外,铺一条宽2米的石子路。
这条石子路的面积是多少平方米?
典型例题
圆环的面积:
20÷2+2=12(m)
π×12 = 144π(m )
答:这条石子路的面积是44π平方米。
S圆环 = S大圆-S小圆
S大圆
S小圆
= πR
= πr
大圆半径(R):
小圆半径(r):
20÷2=10(m)
π×10 = 100π(m )
石子路面积(圆环): 144π -100π = 44π(m )
R
拓展提高
1. 下图中正方形的面积是8平方厘米,你能求出圆的面积吗?
仔细观察,正方形和圆有什么关系呢?
正方形的边长 = 圆的半径
半径×半径 = 正方形的面积
圆的面积 = π×8
S圆 = π r
r = S正 = 8
π×8
r
r
r
= 8π(cm )
拓展提高
2. 下图中直角三角形的面积是4平方厘米,你能求出圆的面积吗?
仔细观察,直角三角形和圆有什么关系呢?
三角形的直角边长 = 圆的半径
半径×半径÷2 = 三角形的面积
圆的面积 = π×4×2
S圆 = π r
r = S三×2
π×4×2
r
r
r ÷2
= 8π(cm )
r = 4 ×2
r = S正 = S三×2 = 4×2
回顾反思
知识梳理
典型例题
拓展提高
名人故事
祖冲之是我国南北朝时期杰出的科学家,
在世界数学史上第一次将圆周率值计算到小
数点后七位数,比国外早了一千多年。据载,
大明八年起,祖冲之出任娄县(今江苏昆山)
令,他为官清正,勤政爱民,为民办了许多
实事、好事。昆山老百姓十分感激他,一直
纪念他,《昆山县志》将他列为“名宦”,
传颂至今。2012年3月,昆山市人大常委会参照国际惯例,把每年的3月14日命名为“祖冲之纪念日”,以纪念我国古代伟大的科学家、圆周率之父——祖冲之。
谢谢观看
圆的整理与复习
苏教版义务教育教科书 数学 五年级下册
课前准备
02
橡皮
01
铅笔
03
尺子
04
自备本
o
r
d
知识梳理
认识
计算
圆
圆
扇形
名称:
圆心
半径
直径
(无数条)
d=2r r=
(相等)
o
r
d
知识梳理
认识
计算
圆
圆
扇形
名称:
圆心
半径
直径
(无数条)
d=2r r=
(相等)
(轴对称图形 无数条对称轴)
o
r
d
画圆:
知识梳理
认识
计算
圆
圆
扇形
名称:
圆心
半径
直径
(无数条)
d=2r r=
(相等)
(轴对称图形 无数条对称轴)
o
r
d
画圆:
定长
定点
旋转一周
知识梳理
认识
计算
圆
圆
扇形
周长
面积
名称:
圆心
半径
直径
画圆:
定长
定点
旋转一周
名称:
弧
圆心角
圆周率(π取近似值3.14)
公式:C=πd C=2πr
组合图形的面积
公式:S=πr
(无数条)
d=2r r=
(相等)
(轴对称图形 无数条对称轴)
同一圆中,圆心角决定扇形的大小。
o
r
d
1
扇形是圆的一部分。
知识梳理
r
S
d
C
d=C÷π
r=d÷2
r=C÷π÷2
C=πd
C=2πr
d=2r
S=πr
圆的计算公式
长方形的面积 = 长 × 宽
=
×
πr2
πr
r
圆的面积
=
S
r
(即πr)
转化
πd 或
=
C
2πr
=
C
化曲为直
实验
未知
已知
典型例题
1. 下图是一个直径是20米的圆形花坛,结合圆的有关知识以及生活实际,
展开想象的翅膀,你能提出哪些数学问题?
(2)圆的周长:
π×20 = 20π(m)
C = πd
(3)圆的面积:
答:花坛的周长是20π米。
(3)花坛的面积是多少平方米?
(2)花坛的周长是多少米?
(1)花坛的半径是多少米?
(1)圆的半径:
20÷2 = 10(m)
r = d÷2
答:花坛的半径是10米。
20÷2 = 10(m)
r = d÷2
S = πr
π×10 = 100π(m )
答:花坛的占地面积是100π平方米。
r
2. 圆圆想在花坛中用篱笆围一块直径是20米的半圆形菜地。
(1)一共需要篱笆多少米?
(2)这块菜地的占地面积是多少平方米?
(1)半圆的周长:
20×3.14÷2 + 20
C半圆 = C圆÷2
(2)半圆的面积:
20÷2 = 10(m)
S半圆 = S圆÷2
π×10 ÷2
+ d
=31.4 + 20
=51.4 (m)
= 100π÷2
= 50π(m )
答:一共需要篱笆51.4米。
答:这块菜地的占地面积是50π平方米。
典型例题
S半圆 = ÷2
S圆
+ d
C半圆 = ÷2
C圆
典型例题
3. 墩墩想在直径20米的圆形花坛外,铺一条宽2米的石子路。
这条石子路的面积是多少平方米?
典型例题
圆环的面积:
20÷2+2=12(m)
π×12 = 144π(m )
答:这条石子路的面积是44π平方米。
S圆环 = S大圆-S小圆
S大圆
S小圆
= πR
= πr
大圆半径(R):
小圆半径(r):
20÷2=10(m)
π×10 = 100π(m )
石子路面积(圆环): 144π -100π = 44π(m )
R
拓展提高
1. 下图中正方形的面积是8平方厘米,你能求出圆的面积吗?
仔细观察,正方形和圆有什么关系呢?
正方形的边长 = 圆的半径
半径×半径 = 正方形的面积
圆的面积 = π×8
S圆 = π r
r = S正 = 8
π×8
r
r
r
= 8π(cm )
拓展提高
2. 下图中直角三角形的面积是4平方厘米,你能求出圆的面积吗?
仔细观察,直角三角形和圆有什么关系呢?
三角形的直角边长 = 圆的半径
半径×半径÷2 = 三角形的面积
圆的面积 = π×4×2
S圆 = π r
r = S三×2
π×4×2
r
r
r ÷2
= 8π(cm )
r = 4 ×2
r = S正 = S三×2 = 4×2
回顾反思
知识梳理
典型例题
拓展提高
名人故事
祖冲之是我国南北朝时期杰出的科学家,
在世界数学史上第一次将圆周率值计算到小
数点后七位数,比国外早了一千多年。据载,
大明八年起,祖冲之出任娄县(今江苏昆山)
令,他为官清正,勤政爱民,为民办了许多
实事、好事。昆山老百姓十分感激他,一直
纪念他,《昆山县志》将他列为“名宦”,
传颂至今。2012年3月,昆山市人大常委会参照国际惯例,把每年的3月14日命名为“祖冲之纪念日”,以纪念我国古代伟大的科学家、圆周率之父——祖冲之。
谢谢观看
