18.1平面展开-最短路径问题的专题训练(附答案解析)
文档属性
| 名称 | 18.1平面展开-最短路径问题的专题训练(附答案解析) |  | |
| 格式 | zip | ||
| 文件大小 | 672.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-22 14:15:07 | ||
图片预览


文档简介
平面展开-最短路径问题 专题训练
一、选择题(共19小题)
1、如图所示,一只小蚂蚁从棱长为1的正方体的顶点A出发,经过每个面的中心点后,又回到A点,蚂蚁爬行最短程S满足( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、5<S≤6 B、6<S≤7
C、7<S≤8 D、8<S≤9
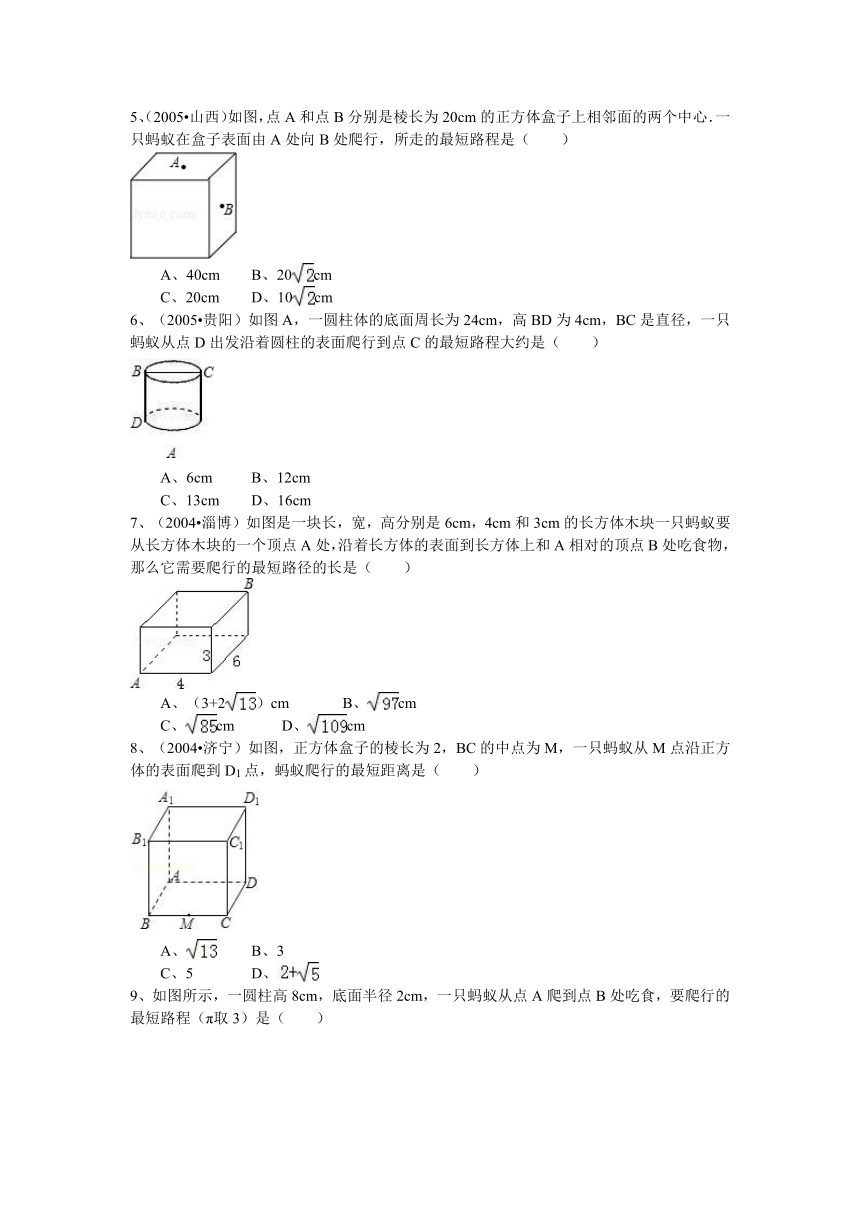
2、(2011 广安)如图,圆柱的底面周长为6cm,AC是底面圆的直径,高BC=6cm,点P是母线BC上一点,且PC=BC.一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、 B、5cm
C、 D、7cm
3、(2009 乐山)如图,一圆锥的底面半径为2,母线PB的长为6,D为PB的中点.一只蚂蚁从点A出发,沿着圆锥的侧面爬行到点D,则蚂蚁爬行的最短路程为( ) ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、 B、2
C、3 D、3
4、(2009 恩施州)如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、5 B、25
C、10+5 D、35
5、(2005 山西)如图,点A和点B分别是棱长为20cm的正方体盒子上相邻面的两个中心.一只蚂蚁在盒子表面由A处向B处爬行,所走的最短路程是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、40cm B、20cm
C、20cm D、10cm
6、(2005 贵阳)如图A,一圆柱体的底面周长为24cm,高BD为4cm,BC是直径,一只蚂蚁从点D出发沿着圆柱的表面爬行到点C的最短路程大约是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、6cm B、12cm
C、13cm D、16cm
7、(2004 淄博)如图是一块长,宽,高分别是6cm,4cm和3cm的长方体木块一只蚂蚁要从长方体木块的一个顶点A处,沿着长方体的表面到长方体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、(3+2)cm B、cm
C、cm D、cm
8、(2004 济宁)如图,正方体盒子的棱长为2,BC的中点为M,一只蚂蚁从M点沿正方体的表面爬到D1点,蚂蚁爬行的最短距离是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、 B、3
C、5 D、
9、如图所示,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程(π取3)是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、12cm B、10cm
C、14cm D、无法确定
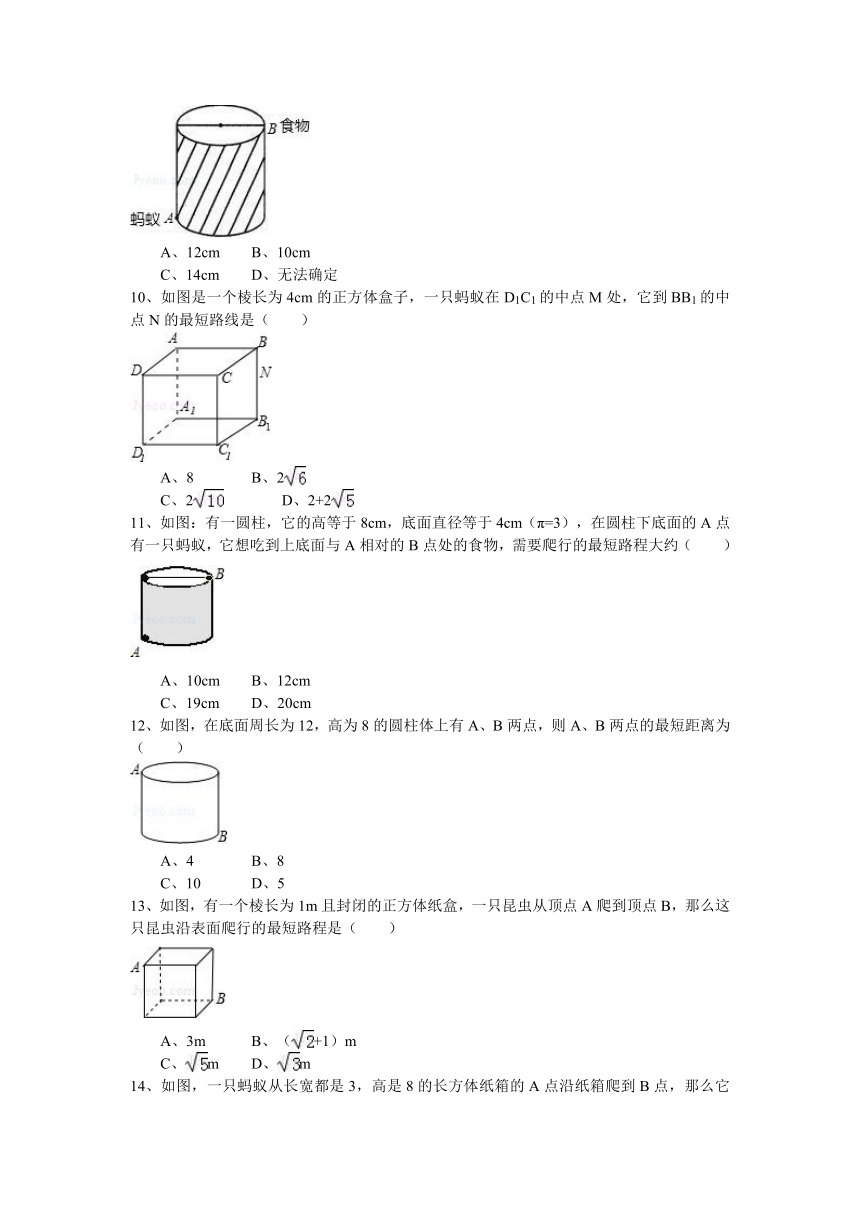
10、如图是一个棱长为4cm的正方体盒子,一只蚂蚁在D1C1的中点M处,它到BB1的中点N的最短路线是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、8 B、2
C、2 D、2+2
11、如图:有一圆柱,它的高等于8cm,底面直径等于4cm(π=3),在圆柱下底面的A点有一只蚂蚁,它想吃到上底面与A相对的B点处的食物,需要爬行的最短路程大约( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、10cm B、12cm
C、19cm D、20cm
12、如图,在底面周长为12,高为8的圆柱体上有A、B两点,则A、B两点的最短距离为( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、4 B、8
C、10 D、5
13、如图,有一个棱长为1m且封闭的正方体纸盒,一只昆虫从顶点A爬到顶点B,那么这只昆虫沿表面爬行的最短路程是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、3m B、(+1)m
C、m D、m
14、如图,一只蚂蚁从长宽都是3,高是8的长方体纸箱的A点沿纸箱爬到B点,那么它所行的最短路线的长是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、(3+8)cm B、10cm
C、14cm D、无法确定
15、如图,棱长为1的正方体,一只蚂蚁从A顶点出发沿着正方体的外表面爬到相对最远的顶点B的最短路程是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、3 B、2
C、 D、
16、如图,边长为1的立方体中,一只蚂蚁从A顶点出发沿着立方体的外表面爬到B顶点的最短路程是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、3 B、
C、 D、1
17、如图,是一块长、宽、高分别是4cm,2cm和1cm的长方体木块、一只蚂蚁要从长方体木块的一个顶点A处,沿着长方体的表面到长方体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、5cm B、5.4cm
C、6.1cm D、7cm
18、如图,点A的正方体左侧面的中心,点B是正方体的一个顶点,正方体的棱长为2,一蚂蚁从点A沿其表面爬到点B的最短路程是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、3 B、
C、 D、4
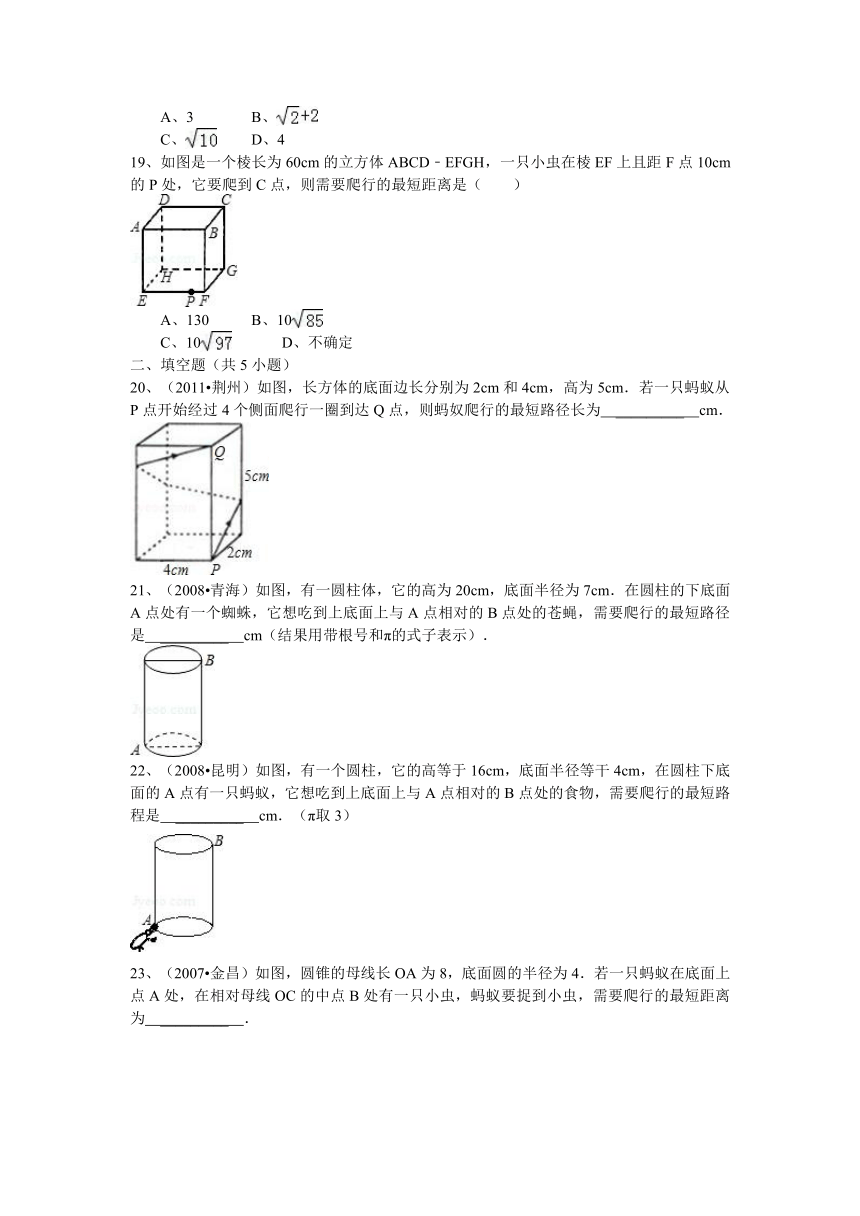
19、如图是一个棱长为60cm的立方体ABCD﹣EFGH,一只小虫在棱EF上且距F点10cm的P处,它要爬到C点,则需要爬行的最短距离是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、130 B、10
C、10 D、不确定
二、填空题(共5小题)
20、(2011 荆州)如图,长方体的底面边长分别为2cm和4cm,高为5cm.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,则蚂奴爬行的最短路径长为 _________ cm.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
21、(2008 青海)如图,有一圆柱体,它的高为20cm,底面半径为7cm.在圆柱的下底面A点处有一个蜘蛛,它想吃到上底面上与A点相对的B点处的苍蝇,需要爬行的最短路径是 _________ cm(结果用带根号和π的式子表示).
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
22、(2008 昆明)如图,有一个圆柱,它的高等于16cm,底面半径等干4cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,需要爬行的最短路程是 _________ cm.(π取3)
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
23、(2007 金昌)如图,圆锥的母线长OA为8,底面圆的半径为4.若一只蚂蚁在底面上点A处,在相对母线OC的中点B处有一只小虫,蚂蚁要捉到小虫,需要爬行的最短距离为 _________ .
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
24、(2006 曲靖)编制一个底面周长为a、高为b的圆柱形花柱架,需用沿圆柱表面绕织一周的竹条若干根,如图中的A1C1B1,A2C2B2,…则每一根这样的竹条的长度最少是 _________ .
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
三、解答题(共6小题)
25、(2007 义乌市)李老师在与同学进行“蚂蚁怎样爬最近”的课题研究时设计了以下三个问题,请你根据下列所给的重要条件分别求出蚂蚁需要爬行的最短路程的长.
(1)如图1,正方体的棱长为5cm一只蚂蚁欲从正方体底面上的点A沿着正方体表面爬到点C1处;
(2)如图2,正四棱柱的底面边长为5cm,侧棱长为6cm,一只蚂蚁从正四棱柱底面上的点A沿着棱柱表面爬到C1处;
(3)如图3,圆锥的母线长为4cm,圆锥的侧面展开图如图4所示,且∠AOA1=120°,一只蚂蚁欲从圆锥的底面上的点A出发,沿圆锥侧面爬行一周回到点A.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
26、(2007 衢州)请阅读下列材料:
问题:如图(1),一圆柱的底面半径、高均为5cm,BC是底面直径,求一只蚂蚁从A点出发沿圆柱表面爬行到点C的最短路线.小明设计了两条路线:
路线1:侧面展开图中的线段AC.如下图(2)所示:
设路线1的长度为l1,则l12=AC2=AB2+2=52+(5π)2=25+25π2
路线2:高线AB+底面直径BC.如上图(1)所示:
设路线2的长度为l2,则l22=(AB+BC)2=(5+10)2=225
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
l12﹣l22=25+25π2﹣225=25π2﹣200=25(π2﹣8)>0
∴l12>l22,∴l1>l2
所以要选择路线2较短.
(1)小明对上述结论有些疑惑,于是他把条件改成:“圆柱的底面半径为1cm,高AB为5cm”继续按前面的路线进行计算.请你帮小明完成下面的计算:
路线1:l12=AC2= _________ ;
路线2:l22=(AB+BC)2= _________
∵l12 _________ l22,
∴l1 _________ l2(填>或<)
∴选择路线 _________ (填1或2)较短.
(2)请你帮小明继续研究:在一般情况下,当圆柱的底面半径为r,高为h时,应如何选择上面的两条路线才能使蚂蚁从点A出发沿圆柱表面爬行到C点的路线最短.
27、(2004 淮安)如图①,一个无盖的正方体盒子的棱长为10厘米,顶点C1处有一只昆虫甲,在盒子的内部顶点A处有一只昆虫乙.(盒壁的厚度忽略不计)
(1)假设昆虫甲在顶点C1处静止不动,如图①,在盒子的内部我们先取棱BB1的中点E,再连接AE、EC1.虫乙如果沿路径A﹣E﹣C1爬行,那么可以在最短的时间内捕捉到昆虫甲.仔细体会其中的道理,并在图①中画出另一条路径,使昆虫乙从顶点A沿这条路径爬行,同样可以在最短的时间内捕捉到昆虫甲;(请简要说明画法)
(2)如图②,假设昆虫甲从顶点C1,以1厘米/秒的速度在盒子的内部沿棱C1C向下爬行,同时昆虫乙从顶点A以2厘米/秒的速度在盒壁上爬行,那么昆虫乙至少需要多长时间才能捕捉到昆虫甲?(精确到1秒)
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
28、一只蚂蚁从长、宽都是30cm,高是80cm的长方体纸箱的A点沿纸箱爬到B点,求它所行的最短路线的长.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
29、有一个如图示的长方体的透明玻璃鱼缸,假设其长AD=80cm,高AB=60cm,水深为AE=40cm,在水面上紧贴内壁G处有一鱼饵,G在水面线EF上,且EG=60cm;一小虫想从鱼缸外的A点沿壁爬进鱼缸内G处吃鱼饵.
(1)小动物应该走怎样的路线才使爬的路线最短呢?请你在图中画出它爬行的路线,并用箭头标注.
(2)求小动物爬行的最短路线长?
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
30、如图,一块长方体砖宽AN=5cm,长ND=10cm,CD上的点B距地面的高BD=8cm,地面上A处的一只蚂蚁到B处吃食,需要爬行的最短路径是多少?
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
答案与评分标准
一、选择题(共19小题)
1、如图所示,一只小蚂蚁从棱长为1的正方体的顶点A出发,经过每个面的中心点后,又回到A点,蚂蚁爬行最短程S满足( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、5<S≤6 B、6<S≤7
C、7<S≤8 D、8<S≤9
考点:勾股定理的应用;平面展开-最短路径问题。
专题:综合题。
分析:先找到A点在正方体展开图形中的对应点,找到6个面的中心点,经观察可知蚂蚁爬行最短程为6个正方体的棱长+展开图形中1个正方形对角线的长.
解答:解:正方体展开图形为:
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
则蚂蚁爬行最短程S=5+=5+.
即6<S≤7.
故选B.
点评:本题考查了平面展开﹣最短路径问题,解题关键是找到A点在正方体展开图形中的对应点及6个面的中心点,有一定的难度.
2、(2011 广安)如图,圆柱的底面周长为6cm,AC是底面圆的直径,高BC=6cm,点P是母线BC上一点,且PC=BC.一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、 B、5cm
C、 D、7cm
考点:平面展开-最短路径问题。
分析:首先画出圆柱的侧面展开图,根据高BC′=6cm,PC=BC,求出PC′=×6=4cm,在Rt△AC′P中,根据勾股定理求出AP的长.
解答:解:侧面展开图如图所示,∵圆柱的底面周长为6cm,
∴AC′=3cm,
∵PC′=BC′,
∴PC′=×6=4cm,
在Rt△ACP中,
AP2=AC′2+CP2,
∴AP==5.
故选B.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
点评:此题主要考查了平面展开图,以及勾股定理的应用,做题的关键是画出圆柱的侧面展开图.
3、(2009 乐山)如图,一圆锥的底面半径为2,母线PB的长为6,D为PB的中点.一只蚂蚁从点A出发,沿着圆锥的侧面爬行到点D,则蚂蚁爬行的最短路程为( ) ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、 B、2
C、3 D、3
考点:平面展开-最短路径问题。
分析:要求蚂蚁爬行的最短距离,需将圆锥的侧面展开,进而根据“两点之间线段最短”得出结果.
解答:解:由题意知,底面圆的直径AB=4,
故底面周长等于4π.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
设圆锥的侧面展开后的扇形圆心角为n°,
根据底面周长等于展开后扇形的弧长得4π=,
解得n=120°,
所以展开图中∠APD=120°÷2=60°,
因为半径PA=PA′,故三角形PAA′为等腰三角形,又∵D为AA′的中点,
所以PD⊥AA′,在直角三角形PAD中,PA=6,PD=3,
根据勾股定理求得AD=3,
所以蚂蚁爬行的最短距离为3.
故选C.
点评:圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.本题就是把圆锥的侧面展开成扇形,“化曲面为平面”,用勾股定理解决.
4、(2009 恩施州)如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、5 B、25
C、10+5 D、35
考点:平面展开-最短路径问题。
分析:要求蚂蚁爬行的最短距离,需将长方体的侧面展开,进而根据“两点之间线段最短”得出结果.
解答:解:将长方体展开,连接A、B,
根据两点之间线段最短,
BD=10+5=15,AD=20,
由勾股定理得:AB====25.
故选B.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
点评:本题是一道趣味题,将长方体展开,根据两点之间线段最短,运用勾股定理解答即可.
5、(2005 山西)如图,点A和点B分别是棱长为20cm的正方体盒子上相邻面的两个中心.一只蚂蚁在盒子表面由A处向B处爬行,所走的最短路程是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、40cm B、20cm
C、20cm D、10cm
考点:平面展开-最短路径问题。
分析:由平面图形的折叠及立体图形的表面展开图的特点解题.
解答:解:
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
根据两点之间线段最短,把正方体展开,可知由A处向B处爬行,所走的最短路程是20cm.
故选C.
点评:熟练掌握两点之间线段最短这一性质.
6、(2005 贵阳)如图A,一圆柱体的底面周长为24cm,高BD为4cm,BC是直径,一只蚂蚁从点D出发沿着圆柱的表面爬行到点C的最短路程大约是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、6cm B、12cm
C、13cm D、16cm
考点:平面展开-最短路径问题。
分析:根据题意,先将圆柱体展开,再根据两点之间线段最短.
解答:解:将圆柱体展开,连接D、C,
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
圆柱体的底面周长为24cm,则DE=12cm,
根据两点之间线段最短,
CD==4≈13cm.
而走B﹣D﹣C的距离更短,
∵BD=4,BC=,
∴BD+BC≈11.64≈12.
故选B.
点评:本题是一道趣味题,将圆柱体展开,根据两点之间线段最短,运用勾股定理解答即可.
7、(2004 淄博)如图是一块长,宽,高分别是6cm,4cm和3cm的长方体木块一只蚂蚁要从长方体木块的一个顶点A处,沿着长方体的表面到长方体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、(3+2)cm B、cm
C、cm D、cm
考点:平面展开-最短路径问题。
分析:作此题要把这个长方体中,蚂蚁所走的路线放到一个平面内,在平面内线段最短,根据勾股定理即可计算.
解答:解:第一种情况:把我们所看到的前面和上面组成一个平面,
则这个长方形的长和宽分别是9和4,
则所走的最短线段是=;
第二种情况:把我们看到的左面与上面组成一个长方形,
则这个长方形的长和宽分别是7和6,
所以走的最短线段是=;
第三种情况:把我们所看到的前面和右面组成一个长方形,
则这个长方形的长和宽分别是10和3,
所以走的最短线段是=;
三种情况比较而言,第二种情况最短.
所以选C.
点评:此题的关键是明确线段最短这一知识点,然后把立体的长方体放到一个平面内,求出最短的线段.
8、(2004 济宁)如图,正方体盒子的棱长为2,BC的中点为M,一只蚂蚁从M点沿正方体的表面爬到D1点,蚂蚁爬行的最短距离是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、 B、3
C、5 D、
考点:平面展开-最短路径问题。
分析:根据题意,先将正方体展开,再根据两点之间线段最短求解.
解答:解:将正方体展开,连接M、D1,
根据两点之间线段最短,
MD=MC+CD=1+2=3,
MD1===.
故选A.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
点评:本题是一道趣味题,将正方体展开,根据两点之间线段最短,运用勾股定理解答即可.
9、如图所示,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程(π取3)是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、12cm B、10cm
C、14cm D、无法确定
考点:平面展开-最短路径问题。
分析:根据两点之间,线段最短.先将图形展开,再根据勾股定理可知.
解答:解:可以把A和B展开到一个平面内,
即圆柱的半个侧面是矩形:
矩形的长是圆柱底面周长的一半即2π=6.
矩形的宽是圆柱的高8.
根据勾股定理得:
爬行的最短路程是矩形的对角线的长,即10.
故选B.
点评:要求不在同一个平面内的两点之间的最短距离,需要把两个点展开到一个平面内,再计算.
10、如图是一个棱长为4cm的正方体盒子,一只蚂蚁在D1C1的中点M处,它到BB1的中点N的最短路线是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、8 B、2
C、2 D、2+2
考点:平面展开-最短路径问题。
分析:把此正方体的DCC1D1面与CC1B1B面展开在同一平面内,然后利用勾股定理求点M和N点间的线段长,即可得到蚂蚁爬行的最短距离.在直角三角形MNB1中,一条直角边长等于6,另一条直角边长等于2,利用勾股定理可求得.
解答:解:把正方体的DCC1D1面与CC1B1B面展开在同一平面内,
∵M、N为C1D1和BB1的中点,
∴NB1=2,MC1=2,
在Rt△NMB1中,MN==2.
故选C.
点评:本题考查了勾股定理的拓展应用.“化曲面为平面”是解决“怎样爬行最近”这类问题的关键.
11、如图:有一圆柱,它的高等于8cm,底面直径等于4cm(π=3),在圆柱下底面的A点有一只蚂蚁,它想吃到上底面与A相对的B点处的食物,需要爬行的最短路程大约( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、10cm B、12cm
C、19cm D、20cm
考点:平面展开-最短路径问题。
分析:根据两点之间,线段最短.首先把A和B展开到一个平面内,即展开圆柱的半个侧面,得到一个矩形,然后根据勾股定理,求得蚂蚁爬行的最短路程即展开矩形的对角线的长度.
解答:解:展开圆柱的半个侧面,得到一个矩形:矩形的长是圆柱底面周长的一半即2π=6,矩形的宽是圆柱的高即8.
根据勾股定理得:蚂蚁爬行的最短路程即展开矩形的对角线长即10.
故选A.
点评:本题考查了勾股定理的拓展应用.“化曲面为平面”是解决“怎样爬行最近”这类问题的关键.本题注意只需展开圆柱的半个侧面.
12、如图,在底面周长为12,高为8的圆柱体上有A、B两点,则A、B两点的最短距离为( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、4 B、8
C、10 D、5
考点:平面展开-最短路径问题。
分析:要求A、B两点间的最短距离,必须展开到一个平面内.只需展开圆柱的半个侧面,然后利用两点之间线段最短解答.
解答:解:展开圆柱的半个侧面,得到一个矩形:矩形的长是圆柱底面周长的一半是6,矩形的宽是圆柱的高是8.再根据勾股定理求得矩形的对角线是10.
即A、B两点间的最短距离是10.
故选C.
点评:要求不在同一个平面内的两点间的最短距离,必须把它们展开到一个平面内再进行计算.
13、如图,有一个棱长为1m且封闭的正方体纸盒,一只昆虫从顶点A爬到顶点B,那么这只昆虫沿表面爬行的最短路程是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、3m B、(+1)m
C、m D、m
考点:平面展开-最短路径问题。
分析:把此正方体的一面展开,然后在平面内,利用勾股定理求点A和B点间的线段长,即可得到蚂蚁爬行的最短距离.在直角三角形中,一条直角边长等于棱长,另一条直角边长等于两条棱长,利用勾股定理可求得.
解答:解:展开后由勾股定理得:AB2=12+(1+1)2=5,故AB=米,
故选C.
点评:本题考查了勾股定理的拓展应用.“化曲面为平面”是解决“怎样爬行最近”这类问题的关键.
14、如图,一只蚂蚁从长宽都是3,高是8的长方体纸箱的A点沿纸箱爬到B点,那么它所行的最短路线的长是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、(3+8)cm B、10cm
C、14cm D、无法确定
考点:平面展开-最短路径问题。
分析:根据”两点之间线段最短”,将点A和点B所在的两个面进行展开,展开为矩形,则AB为矩形的对角线,即蚂蚁所行的最短路线为AB.
解答:解:将点A和点B所在的两个面展开,
则矩形的长和宽分别为6和8,
故矩形对角线长AB==10,
即蚂蚁所行的最短路线长是10.
故选B.
点评:本题的关键是将点A和点B所在的面展开,运用勾股定理求出矩形的对角线.
15、如图,棱长为1的正方体,一只蚂蚁从A顶点出发沿着正方体的外表面爬到相对最远的顶点B的最短路程是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、3 B、2
C、 D、
考点:平面展开-最短路径问题。
分析:要求正方体中两点之间的最短路径,最直接的作法,就是将正方体展开,然后利用两点之间线段最短解答.
解答:解:如图将正方体展开,根据“两点之间,线段最短”知,线段AB即为最短路线.
AB==.
故选C.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
点评:本题主要考查两点之间线段最短.
16、如图,边长为1的立方体中,一只蚂蚁从A顶点出发沿着立方体的外表面爬到B顶点的最短路程是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、3 B、
C、 D、1
考点:平面展开-最短路径问题。
分析:要求正方体中两点之间的最短路径,最直接的作法,就是将正方体展开,然后利用两点之间线段最短解答.
解答:解:如图将正方体展开,根据两点之间,线段最短,
得:最短路程是=.
故选B.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
点评:要求不在同一平面内的两点之间的距离时,首先要把它们展开到一个平面内,然后根据两点之间,线段最短,即可求出最短距离.
17、如图,是一块长、宽、高分别是4cm,2cm和1cm的长方体木块、一只蚂蚁要从长方体木块的一个顶点A处,沿着长方体的表面到长方体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、5cm B、5.4cm
C、6.1cm D、7cm
考点:平面展开-最短路径问题;勾股定理。
分析:把此长方体的一面展开,然后在平面内,利用勾股定理求点A和B点间的线段长,即可得到蚂蚁爬行的最短距离.在直角三角形中,一条直角边长等于长方体的高,另一条直角边长等于长方体的长宽之和,利用勾股定理可求得.
解答:解:因为平面展开图不唯一,故分情况分别计算,进行大、小比较,再从各个路线中确定最短的路线.
(1)展开前面右面由勾股定理得AB2=(2+4)2+12=37;
(2)展开前面上面由勾股定理得AB2=(1+4)2+22=29;
(3)展开左面上面由勾股定理得AB2=(2+1)2+42=25.
所以最短路径的长为AB==5cm.
故选A.
点评:本题考查了勾股定理的拓展应用.“化曲面为平面”是解决“怎样爬行最近”这类问题的关键.
18、如图,点A的正方体左侧面的中心,点B是正方体的一个顶点,正方体的棱长为2,一蚂蚁从点A沿其表面爬到点B的最短路程是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、3 B、
C、 D、4
考点:平面展开-最短路径问题。
分析:将正方体的左侧面与前面展开,构成一个长方形,用勾股定理求出距离即可.
解答:解:如图,AB==.故选C.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
点评:此题求最短路径,我们将平面展开,组成一个直角三角形,利用勾股定理求出斜边就可以了.
19、如图是一个棱长为60cm的立方体ABCD﹣EFGH,一只小虫在棱EF上且距F点10cm的P处,它要爬到C点,则需要爬行的最短距离是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、130 B、10
C、10 D、不确定
考点:平面展开-最短路径问题。
分析:要求正方体中两点之间的最短路径,最直接的作法,就是将正方体展开,然后利用两点之间线段最短解答.
解答:解:展开后可分三种情况,
(1)CP====10;
(2)CP====10;
(3)CP===10=50.
综上所述,最短路径应为(2)所示,CP=10.
故选B.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
点评:解答此题要注意以下几点:
(1)将立体图形展开的能力;
(2)分类讨论思想的应用;
(3)正确运用勾股定理.
二、填空题(共5小题)
20、(2011 荆州)如图,长方体的底面边长分别为2cm和4cm,高为5cm.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,则蚂奴爬行的最短路径长为 13 cm.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
考点:平面展开-最短路径问题。
专题:几何图形问题。
分析:要求长方体中两点之间的最短路径,最直接的作法,就是将长方体展开,然后利用两点之间线段最短解答.
解答:解:
∵PA=2×(4+2)=12,QA=5
∴PQ=13.
故答案为:13.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
点评:本题主要考查两点之间线段最短,以及如何把立体图形转化成平面图形.
21、(2008 青海)如图,有一圆柱体,它的高为20cm,底面半径为7cm.在圆柱的下底面A点处有一个蜘蛛,它想吃到上底面上与A点相对的B点处的苍蝇,需要爬行的最短路径是 cm(结果用带根号和π的式子表示).
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
考点:平面展开-最短路径问题。
分析:要求需要爬行的最短路径首先要把圆柱的侧面积展开,得到一个矩形,然后利用勾股定理求两点间的线段即可.
解答:解:如图所示,把圆柱得侧面展开,得到如图所示的图形,
其中AC=πR=7π,BC=20,
在Rt△ABC中,AB==.
故答案为:.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
点评:本题的关键是理解要求需要爬行的最短路径首先要把圆柱的侧面积展开,底面周长和高以及所走的路线构成一个直角三角形,然后再求线段的长.
22、(2008 昆明)如图,有一个圆柱,它的高等于16cm,底面半径等干4cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,需要爬行的最短路程是 20 cm.(π取3)
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
考点:平面展开-最短路径问题。
分析:先将图形展开,再根据两点之间线段最短可知.
解答:解:将圆柱体展开,连接A、B,根据两点之间线段最短,
则AC=4π=12,
∴AB==20cm.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
点评:本题是一道趣味题,将圆柱体展开,根据两点之间线段最短,运用勾股定理解答即可.
23、(2007 金昌)如图,圆锥的母线长OA为8,底面圆的半径为4.若一只蚂蚁在底面上点A处,在相对母线OC的中点B处有一只小虫,蚂蚁要捉到小虫,需要爬行的最短距离为 .
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
考点:平面展开-最短路径问题。
分析:要求蚂蚁爬行的最短距离,需将圆锥的侧面展开,进而根据“两点之间线段最短”得出结果.
解答:解:由题意知,底面圆的直径AC=8,故底面周长等于8π.
设圆锥的侧面展开后的扇形圆心角为n°,
根据底面周长等于展开后扇形的弧长得,8π=,
解得n=180,所以展开图中∠AOB=90°,
根据勾股定理求得AB=,
所以蚂蚁爬行的最短距离为.
点评:圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.本题就是把圆锥的侧面展开成扇形,“化曲面为平面”,用勾股定理解决.
24、(2006 曲靖)编制一个底面周长为a、高为b的圆柱形花柱架,需用沿圆柱表面绕织一周的竹条若干根,如图中的A1C1B1,A2C2B2,…则每一根这样的竹条的长度最少是 .
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
考点:平面展开-最短路径问题。
分析:圆柱的侧面展开是一个矩形,绕织一周的竹条,最短应是这个矩形的对角线长,与底面周长,高构成直角三角形,所以竹条的长度最少是.
解答:解:底面周长为a、高为b的圆柱形花柱架,如图每一根这样的竹条的长度最少是.
点评:立体图形中的最短距离,通常要转换为平面图形的两点间的线段长来进行解决.
三、解答题(共6小题)
25、(2007 义乌市)李老师在与同学进行“蚂蚁怎样爬最近”的课题研究时设计了以下三个问题,请你根据下列所给的重要条件分别求出蚂蚁需要爬行的最短路程的长.
(1)如图1,正方体的棱长为5cm一只蚂蚁欲从正方体底面上的点A沿着正方体表面爬到点C1处;
(2)如图2,正四棱柱的底面边长为5cm,侧棱长为6cm,一只蚂蚁从正四棱柱底面上的点A沿着棱柱表面爬到C1处;
(3)如图3,圆锥的母线长为4cm,圆锥的侧面展开图如图4所示,且∠AOA1=120°,一只蚂蚁欲从圆锥的底面上的点A出发,沿圆锥侧面爬行一周回到点A.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
考点:平面展开-最短路径问题。
分析:将各图展开,根据两点之间线段最短,利用勾股定理解答.
解答:解:
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
(1);
(2)画图分两种情况:
①当横向剪开时:,
②当竖向剪开时:,
∵,∴最短路程为cm.
(3)由已知得所求的最短的路程为AA1=.
点评:此题考查了同学们的空间想象能力,同时要求同学们能将立体图形侧面展开,有一定难度.
26、(2007 衢州)请阅读下列材料:
问题:如图(1),一圆柱的底面半径、高均为5cm,BC是底面直径,求一只蚂蚁从A点出发沿圆柱表面爬行到点C的最短路线.小明设计了两条路线:
路线1:侧面展开图中的线段AC.如下图(2)所示:
设路线1的长度为l1,则l12=AC2=AB2+2=52+(5π)2=25+25π2
路线2:高线AB+底面直径BC.如上图(1)所示:
设路线2的长度为l2,则l22=(AB+BC)2=(5+10)2=225
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
l12﹣l22=25+25π2﹣225=25π2﹣200=25(π2﹣8)>0
∴l12>l22,∴l1>l2
所以要选择路线2较短.
(1)小明对上述结论有些疑惑,于是他把条件改成:“圆柱的底面半径为1cm,高AB为5cm”继续按前面的路线进行计算.请你帮小明完成下面的计算:
路线1:l12=AC2= 25+π2 ;
路线2:l22=(AB+BC)2= 49
∵l12 < l22,
∴l1 < l2(填>或<)
∴选择路线 1 (填1或2)较短.
(2)请你帮小明继续研究:在一般情况下,当圆柱的底面半径为r,高为h时,应如何选择上面的两条路线才能使蚂蚁从点A出发沿圆柱表面爬行到C点的路线最短.
考点:平面展开-最短路径问题。
专题:阅读型。
分析:(1)根据勾股定理易得路线1 ∈l12=AC2=高2+底面周长一半2;路线2:l22=(高+底面直径)2;让两个平方比较,平方大的,底数就大.
(2)根据(1)得到的结论让两个代数式分三种情况进行比较即可.
解答:解:(1)路线1:l12=AC2=25+π2;路线2:l22=(AB+BC)2=49.
∵l12<l22,
∴l1<l2(填>或<),
∴选择路线1(填1或2)较短.(5分)
(2)l12=AC2=AB2+2=h2+(πr)2,
l22=(AB+BC)2=(h+2r)2,
l12﹣l22=h2+(πr)2﹣(h+2r)2=r(π2r﹣4r﹣4h)=r[(π2﹣4)r﹣4h];
r恒大于0,只需看后面的式子即可.(2分)
当时,l12=l22;
当r>时,l12>l22;
当r<时,l12<l22.
点评:比较两个数的大小,有时比较两个数的平方比较简便,比较两个数的平方,通常让这两个数的平方相减.注意运用类比的方法做类型题.
27、(2004 淮安)如图①,一个无盖的正方体盒子的棱长为10厘米,顶点C1处有一只昆虫甲,在盒子的内部顶点A处有一只昆虫乙.(盒壁的厚度忽略不计)
(1)假设昆虫甲在顶点C1处静止不动,如图①,在盒子的内部我们先取棱BB1的中点E,再连接AE、EC1.虫乙如果沿路径A﹣E﹣C1爬行,那么可以在最短的时间内捕捉到昆虫甲.仔细体会其中的道理,并在图①中画出另一条路径,使昆虫乙从顶点A沿这条路径爬行,同样可以在最短的时间内捕捉到昆虫甲;(请简要说明画法)
(2)如图②,假设昆虫甲从顶点C1,以1厘米/秒的速度在盒子的内部沿棱C1C向下爬行,同时昆虫乙从顶点A以2厘米/秒的速度在盒壁上爬行,那么昆虫乙至少需要多长时间才能捕捉到昆虫甲?(精确到1秒)
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
考点:平面展开-最短路径问题。
专题:压轴题。
分析:(1)当相邻两个面放在同一平面内时,过AC1的线段必过公共棱的中点,按此方法,可画出A,C1所在的相邻面的所有公共棱的中点;
(2)联系(1)中的4个结论,分别画出图形,利用勾股定理求得两点间的最短路线,进而求解.
解答:解:(1)画出图①中A E2 C1,A E3 C1,A E4 C1中任意一条路径;(E1、E2、E3分别为各棱中点)
(说明:无画法,扣2分)
(2)由(1)可知,当昆虫甲从顶点C1沿棱C1C向顶点C爬行的同时,昆虫乙可以沿下列四种路径中的任意一种爬行:
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 ) ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
可以看出,图②﹣1与图②﹣2中的路径相等,图②﹣3与图②﹣4中的路径相等.
①设昆虫甲从顶点C1沿棱C1C向顶点C爬行的同时,昆虫乙从顶点A按路径A→E→F爬行捕捉到昆虫甲需x秒钟,
如图②﹣1﹣1,在Rt△ACF中,
(2x)2=(10﹣x)2+202,
解得x=10;
设昆虫甲从顶点C1沿棱C1C向顶点C爬行的同时,昆虫乙从顶点A按路径A→E2→F爬行捕捉到昆虫甲需y秒钟,
如图②﹣1﹣2,在Rt△ABF中,
(2y)2=(20﹣y)2+102,
解得y≈8;
所以昆虫乙从顶点A爬行捕捉到昆虫甲至少需8秒钟.
[说明]未考虑到A→E→F和图④中其它路径,而直接按路径A→E→F(或A→E→F)计算,并求出正确答案的不扣分.
点评:立体图形中的最短距离,通常要转换为平面图形的两点间的线段长来进行解决.
28、一只蚂蚁从长、宽都是30cm,高是80cm的长方体纸箱的A点沿纸箱爬到B点,求它所行的最短路线的长.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
考点:平面展开-最短路径问题。
分析:要求长方体中两点之间的最短路径,最直接的作法,就是将长方体的侧面展开,然后利用两点之间线段最短解答.
解答:解:蚂蚁实际上是在长方体的半个侧面内爬行,如果将这半个侧面展开如图,得到矩形ACBD,根据“两点之间,线段最短”,所求的最短路程就是半个侧面展开图矩形对角线AB之长.
在Rt△ABC中,AC=底面边长×2=60cm,
∴AB==,
=100(cm),
答:最短路程约为100cm.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
点评:本题主要考查两点之间线段最短及勾股定理,比较简单.
29、有一个如图示的长方体的透明玻璃鱼缸,假设其长AD=80cm,高AB=60cm,水深为AE=40cm,在水面上紧贴内壁G处有一鱼饵,G在水面线EF上,且EG=60cm;一小虫想从鱼缸外的A点沿壁爬进鱼缸内G处吃鱼饵.
(1)小动物应该走怎样的路线才使爬的路线最短呢?请你在图中画出它爬行的路线,并用箭头标注.
(2)求小动物爬行的最短路线长?
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
考点:平面展开-最短路径问题。
专题:计算题。
分析:(1)将矩形BEFC沿BC向上翻折,连接AG,交BC于点N,则小动物从A爬到N,再从N爬到G,路线最短.
(2)求出AG的厂和MG的长相加即可得出结果.
解答:解:(1)如图所示:
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
(2)∵AE=80cm,EG=60cm,
∴AG==100cm.
∴最短路线长为:100cm.
点评:本题考查最短路径问题,关键知道两点之间线段最短,从而可找到路径求出解.
30、如图,一块长方体砖宽AN=5cm,长ND=10cm,CD上的点B距地面的高BD=8cm,地面上A处的一只蚂蚁到B处吃食,需要爬行的最短路径是多少?
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
考点:平面展开-最短路径问题。
分析:要求不在同一平面内的两点间的最短距离,首先要把两点所在的两个平面展开到一个平面内,然后根据题意确定数据,再根据勾股定理即可求解.
解答:解:如图1,在砖的侧面展开图2上,连接AB,
则AB的长即为A处到B处的最短路程.
解:在Rt△ABD中,
因为AD=AN+ND=5+10=15,BD=8,
所以AB2=AD2+BD2=152+82=289=172.
所以AB=17cm.
故蚂蚁爬行的最短路径为17cm.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
点评:此题的难点在于确定两点间的最短距离是什么.
一、选择题(共19小题)
1、如图所示,一只小蚂蚁从棱长为1的正方体的顶点A出发,经过每个面的中心点后,又回到A点,蚂蚁爬行最短程S满足( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、5<S≤6 B、6<S≤7
C、7<S≤8 D、8<S≤9
2、(2011 广安)如图,圆柱的底面周长为6cm,AC是底面圆的直径,高BC=6cm,点P是母线BC上一点,且PC=BC.一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、 B、5cm
C、 D、7cm
3、(2009 乐山)如图,一圆锥的底面半径为2,母线PB的长为6,D为PB的中点.一只蚂蚁从点A出发,沿着圆锥的侧面爬行到点D,则蚂蚁爬行的最短路程为( ) ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、 B、2
C、3 D、3
4、(2009 恩施州)如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、5 B、25
C、10+5 D、35
5、(2005 山西)如图,点A和点B分别是棱长为20cm的正方体盒子上相邻面的两个中心.一只蚂蚁在盒子表面由A处向B处爬行,所走的最短路程是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、40cm B、20cm
C、20cm D、10cm
6、(2005 贵阳)如图A,一圆柱体的底面周长为24cm,高BD为4cm,BC是直径,一只蚂蚁从点D出发沿着圆柱的表面爬行到点C的最短路程大约是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、6cm B、12cm
C、13cm D、16cm
7、(2004 淄博)如图是一块长,宽,高分别是6cm,4cm和3cm的长方体木块一只蚂蚁要从长方体木块的一个顶点A处,沿着长方体的表面到长方体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、(3+2)cm B、cm
C、cm D、cm
8、(2004 济宁)如图,正方体盒子的棱长为2,BC的中点为M,一只蚂蚁从M点沿正方体的表面爬到D1点,蚂蚁爬行的最短距离是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、 B、3
C、5 D、
9、如图所示,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程(π取3)是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、12cm B、10cm
C、14cm D、无法确定
10、如图是一个棱长为4cm的正方体盒子,一只蚂蚁在D1C1的中点M处,它到BB1的中点N的最短路线是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、8 B、2
C、2 D、2+2
11、如图:有一圆柱,它的高等于8cm,底面直径等于4cm(π=3),在圆柱下底面的A点有一只蚂蚁,它想吃到上底面与A相对的B点处的食物,需要爬行的最短路程大约( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、10cm B、12cm
C、19cm D、20cm
12、如图,在底面周长为12,高为8的圆柱体上有A、B两点,则A、B两点的最短距离为( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、4 B、8
C、10 D、5
13、如图,有一个棱长为1m且封闭的正方体纸盒,一只昆虫从顶点A爬到顶点B,那么这只昆虫沿表面爬行的最短路程是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、3m B、(+1)m
C、m D、m
14、如图,一只蚂蚁从长宽都是3,高是8的长方体纸箱的A点沿纸箱爬到B点,那么它所行的最短路线的长是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、(3+8)cm B、10cm
C、14cm D、无法确定
15、如图,棱长为1的正方体,一只蚂蚁从A顶点出发沿着正方体的外表面爬到相对最远的顶点B的最短路程是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、3 B、2
C、 D、
16、如图,边长为1的立方体中,一只蚂蚁从A顶点出发沿着立方体的外表面爬到B顶点的最短路程是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、3 B、
C、 D、1
17、如图,是一块长、宽、高分别是4cm,2cm和1cm的长方体木块、一只蚂蚁要从长方体木块的一个顶点A处,沿着长方体的表面到长方体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、5cm B、5.4cm
C、6.1cm D、7cm
18、如图,点A的正方体左侧面的中心,点B是正方体的一个顶点,正方体的棱长为2,一蚂蚁从点A沿其表面爬到点B的最短路程是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、3 B、
C、 D、4
19、如图是一个棱长为60cm的立方体ABCD﹣EFGH,一只小虫在棱EF上且距F点10cm的P处,它要爬到C点,则需要爬行的最短距离是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、130 B、10
C、10 D、不确定
二、填空题(共5小题)
20、(2011 荆州)如图,长方体的底面边长分别为2cm和4cm,高为5cm.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,则蚂奴爬行的最短路径长为 _________ cm.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
21、(2008 青海)如图,有一圆柱体,它的高为20cm,底面半径为7cm.在圆柱的下底面A点处有一个蜘蛛,它想吃到上底面上与A点相对的B点处的苍蝇,需要爬行的最短路径是 _________ cm(结果用带根号和π的式子表示).
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
22、(2008 昆明)如图,有一个圆柱,它的高等于16cm,底面半径等干4cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,需要爬行的最短路程是 _________ cm.(π取3)
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
23、(2007 金昌)如图,圆锥的母线长OA为8,底面圆的半径为4.若一只蚂蚁在底面上点A处,在相对母线OC的中点B处有一只小虫,蚂蚁要捉到小虫,需要爬行的最短距离为 _________ .
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
24、(2006 曲靖)编制一个底面周长为a、高为b的圆柱形花柱架,需用沿圆柱表面绕织一周的竹条若干根,如图中的A1C1B1,A2C2B2,…则每一根这样的竹条的长度最少是 _________ .
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
三、解答题(共6小题)
25、(2007 义乌市)李老师在与同学进行“蚂蚁怎样爬最近”的课题研究时设计了以下三个问题,请你根据下列所给的重要条件分别求出蚂蚁需要爬行的最短路程的长.
(1)如图1,正方体的棱长为5cm一只蚂蚁欲从正方体底面上的点A沿着正方体表面爬到点C1处;
(2)如图2,正四棱柱的底面边长为5cm,侧棱长为6cm,一只蚂蚁从正四棱柱底面上的点A沿着棱柱表面爬到C1处;
(3)如图3,圆锥的母线长为4cm,圆锥的侧面展开图如图4所示,且∠AOA1=120°,一只蚂蚁欲从圆锥的底面上的点A出发,沿圆锥侧面爬行一周回到点A.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
26、(2007 衢州)请阅读下列材料:
问题:如图(1),一圆柱的底面半径、高均为5cm,BC是底面直径,求一只蚂蚁从A点出发沿圆柱表面爬行到点C的最短路线.小明设计了两条路线:
路线1:侧面展开图中的线段AC.如下图(2)所示:
设路线1的长度为l1,则l12=AC2=AB2+2=52+(5π)2=25+25π2
路线2:高线AB+底面直径BC.如上图(1)所示:
设路线2的长度为l2,则l22=(AB+BC)2=(5+10)2=225
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
l12﹣l22=25+25π2﹣225=25π2﹣200=25(π2﹣8)>0
∴l12>l22,∴l1>l2
所以要选择路线2较短.
(1)小明对上述结论有些疑惑,于是他把条件改成:“圆柱的底面半径为1cm,高AB为5cm”继续按前面的路线进行计算.请你帮小明完成下面的计算:
路线1:l12=AC2= _________ ;
路线2:l22=(AB+BC)2= _________
∵l12 _________ l22,
∴l1 _________ l2(填>或<)
∴选择路线 _________ (填1或2)较短.
(2)请你帮小明继续研究:在一般情况下,当圆柱的底面半径为r,高为h时,应如何选择上面的两条路线才能使蚂蚁从点A出发沿圆柱表面爬行到C点的路线最短.
27、(2004 淮安)如图①,一个无盖的正方体盒子的棱长为10厘米,顶点C1处有一只昆虫甲,在盒子的内部顶点A处有一只昆虫乙.(盒壁的厚度忽略不计)
(1)假设昆虫甲在顶点C1处静止不动,如图①,在盒子的内部我们先取棱BB1的中点E,再连接AE、EC1.虫乙如果沿路径A﹣E﹣C1爬行,那么可以在最短的时间内捕捉到昆虫甲.仔细体会其中的道理,并在图①中画出另一条路径,使昆虫乙从顶点A沿这条路径爬行,同样可以在最短的时间内捕捉到昆虫甲;(请简要说明画法)
(2)如图②,假设昆虫甲从顶点C1,以1厘米/秒的速度在盒子的内部沿棱C1C向下爬行,同时昆虫乙从顶点A以2厘米/秒的速度在盒壁上爬行,那么昆虫乙至少需要多长时间才能捕捉到昆虫甲?(精确到1秒)
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
28、一只蚂蚁从长、宽都是30cm,高是80cm的长方体纸箱的A点沿纸箱爬到B点,求它所行的最短路线的长.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
29、有一个如图示的长方体的透明玻璃鱼缸,假设其长AD=80cm,高AB=60cm,水深为AE=40cm,在水面上紧贴内壁G处有一鱼饵,G在水面线EF上,且EG=60cm;一小虫想从鱼缸外的A点沿壁爬进鱼缸内G处吃鱼饵.
(1)小动物应该走怎样的路线才使爬的路线最短呢?请你在图中画出它爬行的路线,并用箭头标注.
(2)求小动物爬行的最短路线长?
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
30、如图,一块长方体砖宽AN=5cm,长ND=10cm,CD上的点B距地面的高BD=8cm,地面上A处的一只蚂蚁到B处吃食,需要爬行的最短路径是多少?
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
答案与评分标准
一、选择题(共19小题)
1、如图所示,一只小蚂蚁从棱长为1的正方体的顶点A出发,经过每个面的中心点后,又回到A点,蚂蚁爬行最短程S满足( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、5<S≤6 B、6<S≤7
C、7<S≤8 D、8<S≤9
考点:勾股定理的应用;平面展开-最短路径问题。
专题:综合题。
分析:先找到A点在正方体展开图形中的对应点,找到6个面的中心点,经观察可知蚂蚁爬行最短程为6个正方体的棱长+展开图形中1个正方形对角线的长.
解答:解:正方体展开图形为:
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
则蚂蚁爬行最短程S=5+=5+.
即6<S≤7.
故选B.
点评:本题考查了平面展开﹣最短路径问题,解题关键是找到A点在正方体展开图形中的对应点及6个面的中心点,有一定的难度.
2、(2011 广安)如图,圆柱的底面周长为6cm,AC是底面圆的直径,高BC=6cm,点P是母线BC上一点,且PC=BC.一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、 B、5cm
C、 D、7cm
考点:平面展开-最短路径问题。
分析:首先画出圆柱的侧面展开图,根据高BC′=6cm,PC=BC,求出PC′=×6=4cm,在Rt△AC′P中,根据勾股定理求出AP的长.
解答:解:侧面展开图如图所示,∵圆柱的底面周长为6cm,
∴AC′=3cm,
∵PC′=BC′,
∴PC′=×6=4cm,
在Rt△ACP中,
AP2=AC′2+CP2,
∴AP==5.
故选B.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
点评:此题主要考查了平面展开图,以及勾股定理的应用,做题的关键是画出圆柱的侧面展开图.
3、(2009 乐山)如图,一圆锥的底面半径为2,母线PB的长为6,D为PB的中点.一只蚂蚁从点A出发,沿着圆锥的侧面爬行到点D,则蚂蚁爬行的最短路程为( ) ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、 B、2
C、3 D、3
考点:平面展开-最短路径问题。
分析:要求蚂蚁爬行的最短距离,需将圆锥的侧面展开,进而根据“两点之间线段最短”得出结果.
解答:解:由题意知,底面圆的直径AB=4,
故底面周长等于4π.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
设圆锥的侧面展开后的扇形圆心角为n°,
根据底面周长等于展开后扇形的弧长得4π=,
解得n=120°,
所以展开图中∠APD=120°÷2=60°,
因为半径PA=PA′,故三角形PAA′为等腰三角形,又∵D为AA′的中点,
所以PD⊥AA′,在直角三角形PAD中,PA=6,PD=3,
根据勾股定理求得AD=3,
所以蚂蚁爬行的最短距离为3.
故选C.
点评:圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.本题就是把圆锥的侧面展开成扇形,“化曲面为平面”,用勾股定理解决.
4、(2009 恩施州)如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、5 B、25
C、10+5 D、35
考点:平面展开-最短路径问题。
分析:要求蚂蚁爬行的最短距离,需将长方体的侧面展开,进而根据“两点之间线段最短”得出结果.
解答:解:将长方体展开,连接A、B,
根据两点之间线段最短,
BD=10+5=15,AD=20,
由勾股定理得:AB====25.
故选B.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
点评:本题是一道趣味题,将长方体展开,根据两点之间线段最短,运用勾股定理解答即可.
5、(2005 山西)如图,点A和点B分别是棱长为20cm的正方体盒子上相邻面的两个中心.一只蚂蚁在盒子表面由A处向B处爬行,所走的最短路程是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、40cm B、20cm
C、20cm D、10cm
考点:平面展开-最短路径问题。
分析:由平面图形的折叠及立体图形的表面展开图的特点解题.
解答:解:
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
根据两点之间线段最短,把正方体展开,可知由A处向B处爬行,所走的最短路程是20cm.
故选C.
点评:熟练掌握两点之间线段最短这一性质.
6、(2005 贵阳)如图A,一圆柱体的底面周长为24cm,高BD为4cm,BC是直径,一只蚂蚁从点D出发沿着圆柱的表面爬行到点C的最短路程大约是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、6cm B、12cm
C、13cm D、16cm
考点:平面展开-最短路径问题。
分析:根据题意,先将圆柱体展开,再根据两点之间线段最短.
解答:解:将圆柱体展开,连接D、C,
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
圆柱体的底面周长为24cm,则DE=12cm,
根据两点之间线段最短,
CD==4≈13cm.
而走B﹣D﹣C的距离更短,
∵BD=4,BC=,
∴BD+BC≈11.64≈12.
故选B.
点评:本题是一道趣味题,将圆柱体展开,根据两点之间线段最短,运用勾股定理解答即可.
7、(2004 淄博)如图是一块长,宽,高分别是6cm,4cm和3cm的长方体木块一只蚂蚁要从长方体木块的一个顶点A处,沿着长方体的表面到长方体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、(3+2)cm B、cm
C、cm D、cm
考点:平面展开-最短路径问题。
分析:作此题要把这个长方体中,蚂蚁所走的路线放到一个平面内,在平面内线段最短,根据勾股定理即可计算.
解答:解:第一种情况:把我们所看到的前面和上面组成一个平面,
则这个长方形的长和宽分别是9和4,
则所走的最短线段是=;
第二种情况:把我们看到的左面与上面组成一个长方形,
则这个长方形的长和宽分别是7和6,
所以走的最短线段是=;
第三种情况:把我们所看到的前面和右面组成一个长方形,
则这个长方形的长和宽分别是10和3,
所以走的最短线段是=;
三种情况比较而言,第二种情况最短.
所以选C.
点评:此题的关键是明确线段最短这一知识点,然后把立体的长方体放到一个平面内,求出最短的线段.
8、(2004 济宁)如图,正方体盒子的棱长为2,BC的中点为M,一只蚂蚁从M点沿正方体的表面爬到D1点,蚂蚁爬行的最短距离是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、 B、3
C、5 D、
考点:平面展开-最短路径问题。
分析:根据题意,先将正方体展开,再根据两点之间线段最短求解.
解答:解:将正方体展开,连接M、D1,
根据两点之间线段最短,
MD=MC+CD=1+2=3,
MD1===.
故选A.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
点评:本题是一道趣味题,将正方体展开,根据两点之间线段最短,运用勾股定理解答即可.
9、如图所示,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程(π取3)是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、12cm B、10cm
C、14cm D、无法确定
考点:平面展开-最短路径问题。
分析:根据两点之间,线段最短.先将图形展开,再根据勾股定理可知.
解答:解:可以把A和B展开到一个平面内,
即圆柱的半个侧面是矩形:
矩形的长是圆柱底面周长的一半即2π=6.
矩形的宽是圆柱的高8.
根据勾股定理得:
爬行的最短路程是矩形的对角线的长,即10.
故选B.
点评:要求不在同一个平面内的两点之间的最短距离,需要把两个点展开到一个平面内,再计算.
10、如图是一个棱长为4cm的正方体盒子,一只蚂蚁在D1C1的中点M处,它到BB1的中点N的最短路线是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、8 B、2
C、2 D、2+2
考点:平面展开-最短路径问题。
分析:把此正方体的DCC1D1面与CC1B1B面展开在同一平面内,然后利用勾股定理求点M和N点间的线段长,即可得到蚂蚁爬行的最短距离.在直角三角形MNB1中,一条直角边长等于6,另一条直角边长等于2,利用勾股定理可求得.
解答:解:把正方体的DCC1D1面与CC1B1B面展开在同一平面内,
∵M、N为C1D1和BB1的中点,
∴NB1=2,MC1=2,
在Rt△NMB1中,MN==2.
故选C.
点评:本题考查了勾股定理的拓展应用.“化曲面为平面”是解决“怎样爬行最近”这类问题的关键.
11、如图:有一圆柱,它的高等于8cm,底面直径等于4cm(π=3),在圆柱下底面的A点有一只蚂蚁,它想吃到上底面与A相对的B点处的食物,需要爬行的最短路程大约( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、10cm B、12cm
C、19cm D、20cm
考点:平面展开-最短路径问题。
分析:根据两点之间,线段最短.首先把A和B展开到一个平面内,即展开圆柱的半个侧面,得到一个矩形,然后根据勾股定理,求得蚂蚁爬行的最短路程即展开矩形的对角线的长度.
解答:解:展开圆柱的半个侧面,得到一个矩形:矩形的长是圆柱底面周长的一半即2π=6,矩形的宽是圆柱的高即8.
根据勾股定理得:蚂蚁爬行的最短路程即展开矩形的对角线长即10.
故选A.
点评:本题考查了勾股定理的拓展应用.“化曲面为平面”是解决“怎样爬行最近”这类问题的关键.本题注意只需展开圆柱的半个侧面.
12、如图,在底面周长为12,高为8的圆柱体上有A、B两点,则A、B两点的最短距离为( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、4 B、8
C、10 D、5
考点:平面展开-最短路径问题。
分析:要求A、B两点间的最短距离,必须展开到一个平面内.只需展开圆柱的半个侧面,然后利用两点之间线段最短解答.
解答:解:展开圆柱的半个侧面,得到一个矩形:矩形的长是圆柱底面周长的一半是6,矩形的宽是圆柱的高是8.再根据勾股定理求得矩形的对角线是10.
即A、B两点间的最短距离是10.
故选C.
点评:要求不在同一个平面内的两点间的最短距离,必须把它们展开到一个平面内再进行计算.
13、如图,有一个棱长为1m且封闭的正方体纸盒,一只昆虫从顶点A爬到顶点B,那么这只昆虫沿表面爬行的最短路程是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、3m B、(+1)m
C、m D、m
考点:平面展开-最短路径问题。
分析:把此正方体的一面展开,然后在平面内,利用勾股定理求点A和B点间的线段长,即可得到蚂蚁爬行的最短距离.在直角三角形中,一条直角边长等于棱长,另一条直角边长等于两条棱长,利用勾股定理可求得.
解答:解:展开后由勾股定理得:AB2=12+(1+1)2=5,故AB=米,
故选C.
点评:本题考查了勾股定理的拓展应用.“化曲面为平面”是解决“怎样爬行最近”这类问题的关键.
14、如图,一只蚂蚁从长宽都是3,高是8的长方体纸箱的A点沿纸箱爬到B点,那么它所行的最短路线的长是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、(3+8)cm B、10cm
C、14cm D、无法确定
考点:平面展开-最短路径问题。
分析:根据”两点之间线段最短”,将点A和点B所在的两个面进行展开,展开为矩形,则AB为矩形的对角线,即蚂蚁所行的最短路线为AB.
解答:解:将点A和点B所在的两个面展开,
则矩形的长和宽分别为6和8,
故矩形对角线长AB==10,
即蚂蚁所行的最短路线长是10.
故选B.
点评:本题的关键是将点A和点B所在的面展开,运用勾股定理求出矩形的对角线.
15、如图,棱长为1的正方体,一只蚂蚁从A顶点出发沿着正方体的外表面爬到相对最远的顶点B的最短路程是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、3 B、2
C、 D、
考点:平面展开-最短路径问题。
分析:要求正方体中两点之间的最短路径,最直接的作法,就是将正方体展开,然后利用两点之间线段最短解答.
解答:解:如图将正方体展开,根据“两点之间,线段最短”知,线段AB即为最短路线.
AB==.
故选C.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
点评:本题主要考查两点之间线段最短.
16、如图,边长为1的立方体中,一只蚂蚁从A顶点出发沿着立方体的外表面爬到B顶点的最短路程是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、3 B、
C、 D、1
考点:平面展开-最短路径问题。
分析:要求正方体中两点之间的最短路径,最直接的作法,就是将正方体展开,然后利用两点之间线段最短解答.
解答:解:如图将正方体展开,根据两点之间,线段最短,
得:最短路程是=.
故选B.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
点评:要求不在同一平面内的两点之间的距离时,首先要把它们展开到一个平面内,然后根据两点之间,线段最短,即可求出最短距离.
17、如图,是一块长、宽、高分别是4cm,2cm和1cm的长方体木块、一只蚂蚁要从长方体木块的一个顶点A处,沿着长方体的表面到长方体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、5cm B、5.4cm
C、6.1cm D、7cm
考点:平面展开-最短路径问题;勾股定理。
分析:把此长方体的一面展开,然后在平面内,利用勾股定理求点A和B点间的线段长,即可得到蚂蚁爬行的最短距离.在直角三角形中,一条直角边长等于长方体的高,另一条直角边长等于长方体的长宽之和,利用勾股定理可求得.
解答:解:因为平面展开图不唯一,故分情况分别计算,进行大、小比较,再从各个路线中确定最短的路线.
(1)展开前面右面由勾股定理得AB2=(2+4)2+12=37;
(2)展开前面上面由勾股定理得AB2=(1+4)2+22=29;
(3)展开左面上面由勾股定理得AB2=(2+1)2+42=25.
所以最短路径的长为AB==5cm.
故选A.
点评:本题考查了勾股定理的拓展应用.“化曲面为平面”是解决“怎样爬行最近”这类问题的关键.
18、如图,点A的正方体左侧面的中心,点B是正方体的一个顶点,正方体的棱长为2,一蚂蚁从点A沿其表面爬到点B的最短路程是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、3 B、
C、 D、4
考点:平面展开-最短路径问题。
分析:将正方体的左侧面与前面展开,构成一个长方形,用勾股定理求出距离即可.
解答:解:如图,AB==.故选C.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
点评:此题求最短路径,我们将平面展开,组成一个直角三角形,利用勾股定理求出斜边就可以了.
19、如图是一个棱长为60cm的立方体ABCD﹣EFGH,一只小虫在棱EF上且距F点10cm的P处,它要爬到C点,则需要爬行的最短距离是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、130 B、10
C、10 D、不确定
考点:平面展开-最短路径问题。
分析:要求正方体中两点之间的最短路径,最直接的作法,就是将正方体展开,然后利用两点之间线段最短解答.
解答:解:展开后可分三种情况,
(1)CP====10;
(2)CP====10;
(3)CP===10=50.
综上所述,最短路径应为(2)所示,CP=10.
故选B.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
点评:解答此题要注意以下几点:
(1)将立体图形展开的能力;
(2)分类讨论思想的应用;
(3)正确运用勾股定理.
二、填空题(共5小题)
20、(2011 荆州)如图,长方体的底面边长分别为2cm和4cm,高为5cm.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,则蚂奴爬行的最短路径长为 13 cm.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
考点:平面展开-最短路径问题。
专题:几何图形问题。
分析:要求长方体中两点之间的最短路径,最直接的作法,就是将长方体展开,然后利用两点之间线段最短解答.
解答:解:
∵PA=2×(4+2)=12,QA=5
∴PQ=13.
故答案为:13.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
点评:本题主要考查两点之间线段最短,以及如何把立体图形转化成平面图形.
21、(2008 青海)如图,有一圆柱体,它的高为20cm,底面半径为7cm.在圆柱的下底面A点处有一个蜘蛛,它想吃到上底面上与A点相对的B点处的苍蝇,需要爬行的最短路径是 cm(结果用带根号和π的式子表示).
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
考点:平面展开-最短路径问题。
分析:要求需要爬行的最短路径首先要把圆柱的侧面积展开,得到一个矩形,然后利用勾股定理求两点间的线段即可.
解答:解:如图所示,把圆柱得侧面展开,得到如图所示的图形,
其中AC=πR=7π,BC=20,
在Rt△ABC中,AB==.
故答案为:.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
点评:本题的关键是理解要求需要爬行的最短路径首先要把圆柱的侧面积展开,底面周长和高以及所走的路线构成一个直角三角形,然后再求线段的长.
22、(2008 昆明)如图,有一个圆柱,它的高等于16cm,底面半径等干4cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,需要爬行的最短路程是 20 cm.(π取3)
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
考点:平面展开-最短路径问题。
分析:先将图形展开,再根据两点之间线段最短可知.
解答:解:将圆柱体展开,连接A、B,根据两点之间线段最短,
则AC=4π=12,
∴AB==20cm.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
点评:本题是一道趣味题,将圆柱体展开,根据两点之间线段最短,运用勾股定理解答即可.
23、(2007 金昌)如图,圆锥的母线长OA为8,底面圆的半径为4.若一只蚂蚁在底面上点A处,在相对母线OC的中点B处有一只小虫,蚂蚁要捉到小虫,需要爬行的最短距离为 .
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
考点:平面展开-最短路径问题。
分析:要求蚂蚁爬行的最短距离,需将圆锥的侧面展开,进而根据“两点之间线段最短”得出结果.
解答:解:由题意知,底面圆的直径AC=8,故底面周长等于8π.
设圆锥的侧面展开后的扇形圆心角为n°,
根据底面周长等于展开后扇形的弧长得,8π=,
解得n=180,所以展开图中∠AOB=90°,
根据勾股定理求得AB=,
所以蚂蚁爬行的最短距离为.
点评:圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.本题就是把圆锥的侧面展开成扇形,“化曲面为平面”,用勾股定理解决.
24、(2006 曲靖)编制一个底面周长为a、高为b的圆柱形花柱架,需用沿圆柱表面绕织一周的竹条若干根,如图中的A1C1B1,A2C2B2,…则每一根这样的竹条的长度最少是 .
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
考点:平面展开-最短路径问题。
分析:圆柱的侧面展开是一个矩形,绕织一周的竹条,最短应是这个矩形的对角线长,与底面周长,高构成直角三角形,所以竹条的长度最少是.
解答:解:底面周长为a、高为b的圆柱形花柱架,如图每一根这样的竹条的长度最少是.
点评:立体图形中的最短距离,通常要转换为平面图形的两点间的线段长来进行解决.
三、解答题(共6小题)
25、(2007 义乌市)李老师在与同学进行“蚂蚁怎样爬最近”的课题研究时设计了以下三个问题,请你根据下列所给的重要条件分别求出蚂蚁需要爬行的最短路程的长.
(1)如图1,正方体的棱长为5cm一只蚂蚁欲从正方体底面上的点A沿着正方体表面爬到点C1处;
(2)如图2,正四棱柱的底面边长为5cm,侧棱长为6cm,一只蚂蚁从正四棱柱底面上的点A沿着棱柱表面爬到C1处;
(3)如图3,圆锥的母线长为4cm,圆锥的侧面展开图如图4所示,且∠AOA1=120°,一只蚂蚁欲从圆锥的底面上的点A出发,沿圆锥侧面爬行一周回到点A.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
考点:平面展开-最短路径问题。
分析:将各图展开,根据两点之间线段最短,利用勾股定理解答.
解答:解:
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
(1);
(2)画图分两种情况:
①当横向剪开时:,
②当竖向剪开时:,
∵,∴最短路程为cm.
(3)由已知得所求的最短的路程为AA1=.
点评:此题考查了同学们的空间想象能力,同时要求同学们能将立体图形侧面展开,有一定难度.
26、(2007 衢州)请阅读下列材料:
问题:如图(1),一圆柱的底面半径、高均为5cm,BC是底面直径,求一只蚂蚁从A点出发沿圆柱表面爬行到点C的最短路线.小明设计了两条路线:
路线1:侧面展开图中的线段AC.如下图(2)所示:
设路线1的长度为l1,则l12=AC2=AB2+2=52+(5π)2=25+25π2
路线2:高线AB+底面直径BC.如上图(1)所示:
设路线2的长度为l2,则l22=(AB+BC)2=(5+10)2=225
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
l12﹣l22=25+25π2﹣225=25π2﹣200=25(π2﹣8)>0
∴l12>l22,∴l1>l2
所以要选择路线2较短.
(1)小明对上述结论有些疑惑,于是他把条件改成:“圆柱的底面半径为1cm,高AB为5cm”继续按前面的路线进行计算.请你帮小明完成下面的计算:
路线1:l12=AC2= 25+π2 ;
路线2:l22=(AB+BC)2= 49
∵l12 < l22,
∴l1 < l2(填>或<)
∴选择路线 1 (填1或2)较短.
(2)请你帮小明继续研究:在一般情况下,当圆柱的底面半径为r,高为h时,应如何选择上面的两条路线才能使蚂蚁从点A出发沿圆柱表面爬行到C点的路线最短.
考点:平面展开-最短路径问题。
专题:阅读型。
分析:(1)根据勾股定理易得路线1 ∈l12=AC2=高2+底面周长一半2;路线2:l22=(高+底面直径)2;让两个平方比较,平方大的,底数就大.
(2)根据(1)得到的结论让两个代数式分三种情况进行比较即可.
解答:解:(1)路线1:l12=AC2=25+π2;路线2:l22=(AB+BC)2=49.
∵l12<l22,
∴l1<l2(填>或<),
∴选择路线1(填1或2)较短.(5分)
(2)l12=AC2=AB2+2=h2+(πr)2,
l22=(AB+BC)2=(h+2r)2,
l12﹣l22=h2+(πr)2﹣(h+2r)2=r(π2r﹣4r﹣4h)=r[(π2﹣4)r﹣4h];
r恒大于0,只需看后面的式子即可.(2分)
当时,l12=l22;
当r>时,l12>l22;
当r<时,l12<l22.
点评:比较两个数的大小,有时比较两个数的平方比较简便,比较两个数的平方,通常让这两个数的平方相减.注意运用类比的方法做类型题.
27、(2004 淮安)如图①,一个无盖的正方体盒子的棱长为10厘米,顶点C1处有一只昆虫甲,在盒子的内部顶点A处有一只昆虫乙.(盒壁的厚度忽略不计)
(1)假设昆虫甲在顶点C1处静止不动,如图①,在盒子的内部我们先取棱BB1的中点E,再连接AE、EC1.虫乙如果沿路径A﹣E﹣C1爬行,那么可以在最短的时间内捕捉到昆虫甲.仔细体会其中的道理,并在图①中画出另一条路径,使昆虫乙从顶点A沿这条路径爬行,同样可以在最短的时间内捕捉到昆虫甲;(请简要说明画法)
(2)如图②,假设昆虫甲从顶点C1,以1厘米/秒的速度在盒子的内部沿棱C1C向下爬行,同时昆虫乙从顶点A以2厘米/秒的速度在盒壁上爬行,那么昆虫乙至少需要多长时间才能捕捉到昆虫甲?(精确到1秒)
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
考点:平面展开-最短路径问题。
专题:压轴题。
分析:(1)当相邻两个面放在同一平面内时,过AC1的线段必过公共棱的中点,按此方法,可画出A,C1所在的相邻面的所有公共棱的中点;
(2)联系(1)中的4个结论,分别画出图形,利用勾股定理求得两点间的最短路线,进而求解.
解答:解:(1)画出图①中A E2 C1,A E3 C1,A E4 C1中任意一条路径;(E1、E2、E3分别为各棱中点)
(说明:无画法,扣2分)
(2)由(1)可知,当昆虫甲从顶点C1沿棱C1C向顶点C爬行的同时,昆虫乙可以沿下列四种路径中的任意一种爬行:
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 ) ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
可以看出,图②﹣1与图②﹣2中的路径相等,图②﹣3与图②﹣4中的路径相等.
①设昆虫甲从顶点C1沿棱C1C向顶点C爬行的同时,昆虫乙从顶点A按路径A→E→F爬行捕捉到昆虫甲需x秒钟,
如图②﹣1﹣1,在Rt△ACF中,
(2x)2=(10﹣x)2+202,
解得x=10;
设昆虫甲从顶点C1沿棱C1C向顶点C爬行的同时,昆虫乙从顶点A按路径A→E2→F爬行捕捉到昆虫甲需y秒钟,
如图②﹣1﹣2,在Rt△ABF中,
(2y)2=(20﹣y)2+102,
解得y≈8;
所以昆虫乙从顶点A爬行捕捉到昆虫甲至少需8秒钟.
[说明]未考虑到A→E→F和图④中其它路径,而直接按路径A→E→F(或A→E→F)计算,并求出正确答案的不扣分.
点评:立体图形中的最短距离,通常要转换为平面图形的两点间的线段长来进行解决.
28、一只蚂蚁从长、宽都是30cm,高是80cm的长方体纸箱的A点沿纸箱爬到B点,求它所行的最短路线的长.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
考点:平面展开-最短路径问题。
分析:要求长方体中两点之间的最短路径,最直接的作法,就是将长方体的侧面展开,然后利用两点之间线段最短解答.
解答:解:蚂蚁实际上是在长方体的半个侧面内爬行,如果将这半个侧面展开如图,得到矩形ACBD,根据“两点之间,线段最短”,所求的最短路程就是半个侧面展开图矩形对角线AB之长.
在Rt△ABC中,AC=底面边长×2=60cm,
∴AB==,
=100(cm),
答:最短路程约为100cm.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
点评:本题主要考查两点之间线段最短及勾股定理,比较简单.
29、有一个如图示的长方体的透明玻璃鱼缸,假设其长AD=80cm,高AB=60cm,水深为AE=40cm,在水面上紧贴内壁G处有一鱼饵,G在水面线EF上,且EG=60cm;一小虫想从鱼缸外的A点沿壁爬进鱼缸内G处吃鱼饵.
(1)小动物应该走怎样的路线才使爬的路线最短呢?请你在图中画出它爬行的路线,并用箭头标注.
(2)求小动物爬行的最短路线长?
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
考点:平面展开-最短路径问题。
专题:计算题。
分析:(1)将矩形BEFC沿BC向上翻折,连接AG,交BC于点N,则小动物从A爬到N,再从N爬到G,路线最短.
(2)求出AG的厂和MG的长相加即可得出结果.
解答:解:(1)如图所示:
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
(2)∵AE=80cm,EG=60cm,
∴AG==100cm.
∴最短路线长为:100cm.
点评:本题考查最短路径问题,关键知道两点之间线段最短,从而可找到路径求出解.
30、如图,一块长方体砖宽AN=5cm,长ND=10cm,CD上的点B距地面的高BD=8cm,地面上A处的一只蚂蚁到B处吃食,需要爬行的最短路径是多少?
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
考点:平面展开-最短路径问题。
分析:要求不在同一平面内的两点间的最短距离,首先要把两点所在的两个平面展开到一个平面内,然后根据题意确定数据,再根据勾股定理即可求解.
解答:解:如图1,在砖的侧面展开图2上,连接AB,
则AB的长即为A处到B处的最短路程.
解:在Rt△ABD中,
因为AD=AN+ND=5+10=15,BD=8,
所以AB2=AD2+BD2=152+82=289=172.
所以AB=17cm.
故蚂蚁爬行的最短路径为17cm.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
点评:此题的难点在于确定两点间的最短距离是什么.
