18.1勾股定理的专题训练(附答案解析)
文档属性
| 名称 | 18.1勾股定理的专题训练(附答案解析) |  | |
| 格式 | zip | ||
| 文件大小 | 326.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-22 14:18:42 | ||
图片预览




文档简介
勾股定理 专题训练
一、解答题(共10小题)
1、在△ABC中,AB=40,AC=60,以A为圆心,AB的长为半径作圆交BC边于D,若BD和DC的长均为正整数,求BC的长.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
2、周长为6,面积为整数的直角三角形是否存在?若不存在,请给出证明;若存在,请证明共有几个?
3、已知Rt△ABC的两条直角边的长a、b均为整数,且a为质数,若斜边c也是整数,求证:2(a+b+1)是完全平方数.
4、已知下面著名的“勾股定理”:在一个直角三角形中,两条直角边的平方之和等于斜边的平方.
试问:是否存在同时满足下列两个条件的直角三角形?
(1)三条边长均是正整数;
(2)一条直角边为素数(也称质数)p.若存在,请求出另一条直角边长;若不存在,请说明理由.
5、设直角三角形的两条直角边长分别为a,b,斜边长为c.若a,b,c均为整数,且c=ab﹣(a+b),求满足条件的直角三角形的个数.
6、已知直角三角形的边长是正整数,并且周长的数值等于这个三角形面积的数值,求斜边的长.
7、在一个半径为20cm的圆形铁板上,欲截取一面积最大的正方形铁板作机器零件,求正方形的边长(精确到0.1).
8、一个直角三角形的边长都是整数,它的面积和周长的数值相等.试确定这个直角三角形三边的长.
9、500多年前,数学各学派的学者都认为世界上的数只有整数和分数,直到有一天,大数学家毕达哥拉斯的一个名叫希帕索斯的学生,在研究1和2的比例中项时(若1:x=x:2,那么x叫1和2的比例中项),他怎么也想不出这个比例中项值.后来,他画了一个边长为1的正方形,设对角线为x,于是由毕达哥拉斯定理x2=12+12=2,他想x代表对角线的长,而x2=2,那么x必定是确定的数,这时他又为自己提出了几个问题:
(1)x是整数吗?为什么不是?
(2)x可能是分数吗?是,能找出来吗?不是,能说出理由吗?亲爱的同学,你能帮他解答这些问题吗?
10、操作画图题
如图,正方形网格中的每个正方形边长都是1,每个小格的顶点叫格点,以格点为顶点,按要求画三角形:使三角形的三边长分别为3、2、(画一个即可).
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
二、填空题(共9小题)
11、两条直角边长分别是整数a,b(其中b<2011),斜边长是b+1的直角三角形的个数为 _________ .
12、已知直角三角形有一边是11,另两边的长度均为自然数,那么这个三角形的周长是 _________ .
13、在边长为1cm的正△ABC中,P0为BC边上一点,作P0P1⊥CA于点 P1,作P1P2⊥AB于点P2,作P2P3⊥BC于点P3.如果点P3恰与点P0重合,则△P1P2P3的面积是 _________ cm2.
14、已知直角三角形两边x,y的长满足|x2﹣4|+=0,则第三边长为 _________ .
15、如图,正方形BCDE和ABFG的边长分别为2a,a,连接CE和CG,则图中阴影部分的面积是 _________ ;CE和CG的大小关系 _________ .
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
16、(2008 荆门)如图,半圆的直径AB= _________ .
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
17、如图,以数轴的单位长线段为边作一个正方形,以数轴的原点为旋转中心,将过原点的对角线顺时针旋转,使对角线的另一端点落在数轴正半轴的点A处,则点A表示的数是 _________ .
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
18、如图,以数轴的单位长线段为边作两个正方形,以数轴的原点为圆心,矩形对角线为半径画弧,交数轴负半轴于点A,则在数轴上A表示的数是 _________ .
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
19、如图,数轴上点A表示的数据为 _________ .
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
三、选择题(共11小题)
20、张大爷离家出门散步,他先向正东走了30m,接着又向正南走了40m,此时他离家的距离为( )
A、30m B、40m
C、50m D、70m
21、如图,已知矩形A′BOC的边长A′B=2,OB=1,数轴上点A表示的数为x,则x2﹣13的立方根是( ) ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、﹣13 B、﹣﹣13
C、2 D、﹣2
22、如图,以数轴的单位长线段为边作一个正方形,以数轴的原点为旋转中心,将过原点的对角线顺时针旋转,使对角线的另一端点落在数轴正半轴的点A处,则点A表示的数是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、 B、1.4
C、 D、
23、如图,以数轴的单位长度线段为边作一个正方形,以表示数1的点为圆心,正方形对角线长为半径画弧,交数轴于点A,则点A表示的数是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、 B、﹣1+
C、﹣1 D、1
24、如图,正方形OABC的边长为1,以A为圆心,AC为半径画弧,与数轴的一个交点是D,则D点表示的数为( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、 B、
C、 D、
25、(2004 广州)如图,在△ABC中,三边a,b,c的大小关系是( ) ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、a<b<c B、c<a<b
C、c<b<a D、b<a<c
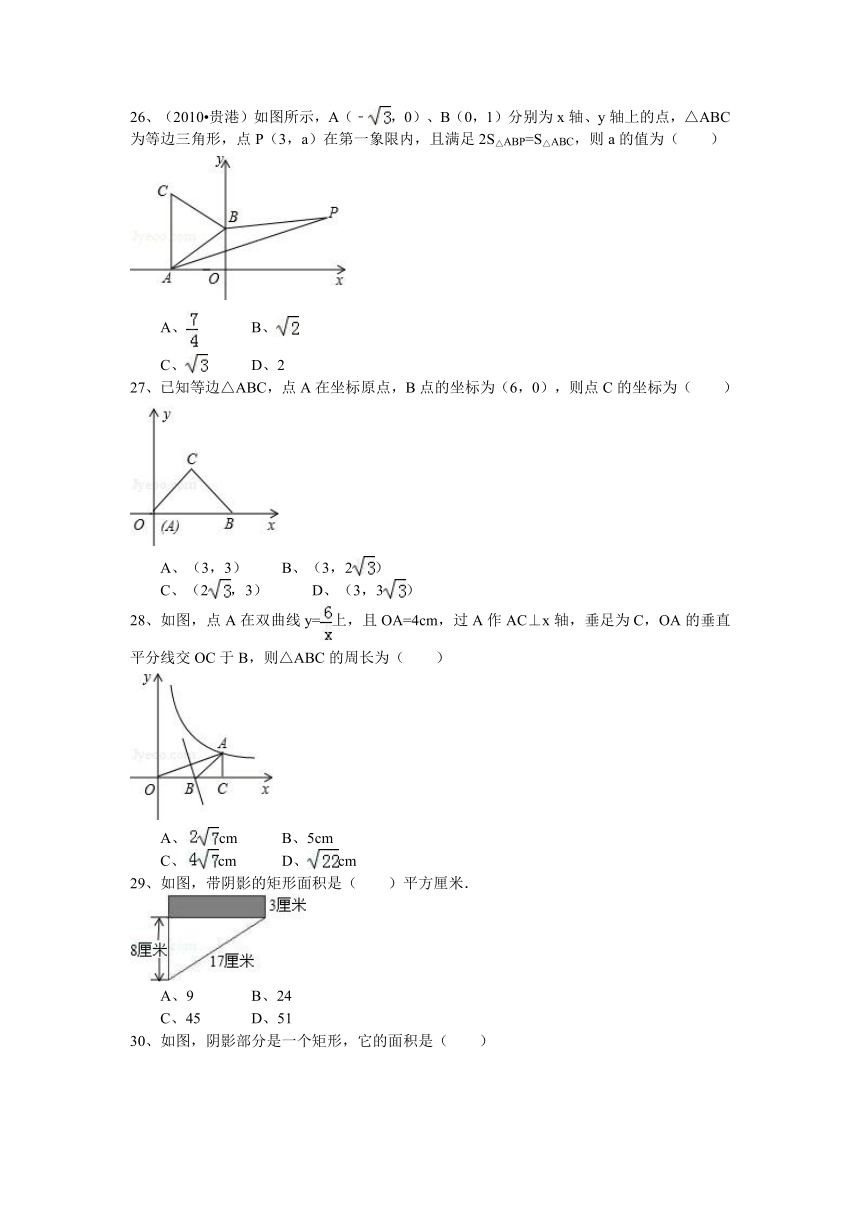
26、(2010 贵港)如图所示,A(﹣,0)、B(0,1)分别为x轴、y轴上的点,△ABC为等边三角形,点P(3,a)在第一象限内,且满足2S△ABP=S△ABC,则a的值为( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、 B、
C、 D、2
27、已知等边△ABC,点A在坐标原点,B点的坐标为(6,0),则点C的坐标为( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、(3,3) B、(3,2)
C、(2,3) D、(3,3)
28、如图,点A在双曲线y=上,且OA=4cm,过A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于B,则△ABC的周长为( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、cm B、5cm
C、cm D、cm
29、如图,带阴影的矩形面积是( )平方厘米.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、9 B、24
C、45 D、51
30、如图,阴影部分是一个矩形,它的面积是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、5cm2 B、3cm2
C、4cm2 D、6cm2
答案与评分标准
一、解答题(共10小题)
1、在△ABC中,AB=40,AC=60,以A为圆心,AB的长为半径作圆交BC边于D,若BD和DC的长均为正整数,求BC的长.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
考点:数的整除性问题;等边三角形的性质;勾股定理。
专题:计算题。
分析:首先假设出BD,CD的长度,再利用勾股定理得出a+b与b的乘积为2000,再利用三角形三边关系得出20<a+b<100,进一步得出a+b的值.
解答:解:设BD=a,CD=b,(a,b为正整数)
作AE⊥BD,垂足为E,则AB=AD=40,BE=DE=.
∵,,
∴,
∴(a+b)b=2000=24×53,
∵20<a+b<100,
∴只有或
故BC的长为50或80.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
点评:此题主要考查了数的整除性知识,以及勾股定理的应用和三角形三边关系,题目综合性较强.
2、周长为6,面积为整数的直角三角形是否存在?若不存在,请给出证明;若存在,请证明共有几个?
考点:非一次不定方程(组);勾股定理。
专题:证明题;探究型。
分析:设存在如上的直角三角形,设两直角边分别为a,b,斜边为c,根据题意可得出关于a、b、c的方程,由勾股定理可判断出c的取值范围,进而求出c的值,把c的值代入不定方程即可求出b、c的值,找出符合条件的未知数的对应值即可.
解答:解:设存在如上的直角三角形,设两直角边分别为a,b,斜边为c,
∵a+b+c=6(1);
a2+b2=c2(2)
∴(a+b)2=(6﹣c)2(3)
∵ab=9﹣3c为整数,
∴c为整数或以3为分母的分数;
∵直角三角形斜边最长则有c>2,根据三角形三边边长规律有c<3;
∴2<c<3;
∴c应为以3为分母的分数,a=或;
当c=时,根据(1)(2)式有:b=6或,a=﹣或,不合题意.
当c=时,根据(1)(2)式有:b=,a=或a=,b=,
∴这样的直角三角形存在,恰有一个,两条直角边为与,斜边为.
点评:本题考查的是非一次不定方程及勾股定理,根据题意判断出c的值是解答此题的关键.
3、已知Rt△ABC的两条直角边的长a、b均为整数,且a为质数,若斜边c也是整数,求证:2(a+b+1)是完全平方数.
考点:完全平方数;勾股定理。
专题:证明题。
分析:由勾股定理易得a2+b2=c2,则a2=c2﹣b2=(c+b)(c﹣b),因为a为质数,所以c+b=a2,c﹣b=1,两式相减可得a2=2b+1,代入2(a+b+1)即可得证.
解答:解:∵a,b是Rt△ABC的两条直角边,c是斜边,
∴a2+b2=c2,
即a2=c2﹣b2=(c+b)(c﹣b),
∵a为质数,
∴c+b=a2,c﹣b=1,
∴a2=2b+1,
∴2(a+b+1)=a2+2a+1=(a+1)2,
∴2(a+b+1)是完全平方数.
点评:此题考查完全平方数,根据勾股定理和a为质数展开答题,是关键.
4、已知下面著名的“勾股定理”:在一个直角三角形中,两条直角边的平方之和等于斜边的平方.
试问:是否存在同时满足下列两个条件的直角三角形?
(1)三条边长均是正整数;
(2)一条直角边为素数(也称质数)p.若存在,请求出另一条直角边长;若不存在,请说明理由.
考点:质数与合数;勾股定理。
专题:计算题。
分析:首先假设存在,设另一条直角边长为x,斜边长为y,则x、y为正整数,然后根据题意可得:p2+x2=y2,即可得:(y+x)(y﹣x)=p2,又由p为素数,讨论分析即可求得.
解答:解:假设存在,令另一条直角边长为x,斜边长为y,则x、y为正整数.
由勾股定理得p2+x2=y2.
化为(y+x)(y﹣x)=p2.
因为p为素数(也称质数),且y+x>y﹣x,
所以只有
从而.
若p=2,则x、y不是整数,这样的三角形不存在;
若p为奇素数,x、y都是整数,这样的三角形存在.
综上所述,可知:p为偶素数2时,满足条件的三角形不存在;p为奇素数时,满足条件的三角形存在,且另一条直角边长为.
点评:此题考查了素数的意义和勾股定理等知识.难度较大,要注意分类讨论思想的应用.
5、设直角三角形的两条直角边长分别为a,b,斜边长为c.若a,b,c均为整数,且c=ab﹣(a+b),求满足条件的直角三角形的个数.
考点:非一次不定方程(组);勾股定理。
专题:探究型。
分析:先根据此三角形是直角三角形,利用勾股定理把原式化为(a﹣6)(b﹣6)=18,再根据a,b均为正整数,不妨设a<b,可得出关于a、b的二元一次方程,求出a、b、c的对应值即可.
解答:解:由勾股定理得,c2=a2+b2.
又∵c=ab﹣(a+b),得.
即.
整理得,ab﹣6(a+b)+18=0,即(a﹣6)(b﹣6)=18,
∵a,b均为正整数,不妨设a<b,
可得或或,
可解出或或,
∴满足条件的直角三角形有3个.
故答案为:3.
点评:本题考查的是非一次不定方程及勾股定理,解答此题的关键是先利用勾股定理把原式化为两个因式积的形式,再根据a,b均为正整数进行解答.
6、已知直角三角形的边长是正整数,并且周长的数值等于这个三角形面积的数值,求斜边的长.
考点:一元二次方程的整数根与有理根;勾股定理。
专题:计算题;分类讨论。
分析:首先根据题目设出未知数a,b,在根据勾股定理a2+b2=c2列出等式,再把其进行化简,用含a的代数式表示b,因为边长都是整数,所以分情况讨论时,取整数情况即可.
解答:解:设直角边为a,b 由题意得:
=a+b+
移项,平方并化简得到:
+2ab﹣ab(a+b)=0
∵ab≠0
∴a+b﹣=2
b===4+
∵b是正整数
∴①a=5,b=12,c=13
②a=6,b=8,c=10
③a=8,b=6,c=10
④a=12,b=5,c=13
∴符合题意的直角三角形的斜边长10或13.
点评:此题主要考查了勾股定理与求方程的整数解的综合运用,用到了数学中的分类讨论思想,注注意讨论是要考虑全面.
7、在一个半径为20cm的圆形铁板上,欲截取一面积最大的正方形铁板作机器零件,求正方形的边长(精确到0.1).
考点:平方根;勾股定理。
分析:正方形的四个顶点都正好在圆板的外沿上时,所截正方形面积最大,此时正方形的对角线为圆的直径,根据勾股定理求解即可.
解答:解:正方形的四个顶点都正好在圆板的外沿上时,所截正方形面积最大,
此时正方形的对角线应是圆的直径.设正方形的边长为xcm,
由题意,得x2+x2=402,解得x=±20(负值舍去).
∴x=20≈20×1.414=28.28≈28.3cm.
∴正方形的边长28.3cm.
点评:本题考查了平方根和勾股定理的运用,属于常见的题型,需要熟练掌握.
8、一个直角三角形的边长都是整数,它的面积和周长的数值相等.试确定这个直角三角形三边的长.
考点:三角形边角关系;勾股定理。
专题:计算题。
分析:设符合条件的直角三角形的三边长为a、b、c,其中c为斜边,则a2+b2=c2,a+b+c=,于是将存在性问题的讨论转化为求方程组的解.
解答:解:假设符合条件的直角三角形存在,它的三边长为a、b、c,其中c为斜边,则
a2+b2=c2,a+b+c=,
∵a、b、c均为正整数,
∴a≠b;不妨设a>b,则有a+b+=,
两边平方,并整理得,
﹣a2b﹣ab2+2ab=0,
消去ab,得
﹣a﹣b+2=0,即(a﹣4)(b﹣4)=8,
又∵8=1×8=2×4,
∴①a﹣4=8,b﹣4=1,解得:a=12,b=5,则c=13;
②a﹣4=4,b﹣4=2,解得:a=8,b=6,则c=10;
综上所述,符合条件的直角三角形的边长分别是5、12、13;6、8、10.
点评:本题主要考查了一元二次方程的整数根及有理根、勾股定理的逆定理的应用.在解题过程中,当勾股定理不能直接运用时,常需要通过等线段的代换、作辅助垂线等途径,为勾股定理的运用创造必要的条件,有时又需要由线段的数量关系去判断线段的位置关系,这就需要熟悉一些常用的勾股数组.
9、500多年前,数学各学派的学者都认为世界上的数只有整数和分数,直到有一天,大数学家毕达哥拉斯的一个名叫希帕索斯的学生,在研究1和2的比例中项时(若1:x=x:2,那么x叫1和2的比例中项),他怎么也想不出这个比例中项值.后来,他画了一个边长为1的正方形,设对角线为x,于是由毕达哥拉斯定理x2=12+12=2,他想x代表对角线的长,而x2=2,那么x必定是确定的数,这时他又为自己提出了几个问题:
(1)x是整数吗?为什么不是?
(2)x可能是分数吗?是,能找出来吗?不是,能说出理由吗?亲爱的同学,你能帮他解答这些问题吗?
考点:无理数;勾股定理。
专题:常规题型。
分析:(1)根据比例中项的定义,可知x2=2,结合无理数的概念,就能得出x是不是整数的结论.
(2)根据分数的定义,任何分数的平方还是分数,即能得出结论.
解答:解:(1)不是,∵1<2<4,而x2=2
∴1<x2<4,若x>0,1<x<2,
∴在1和2之间不存在另外的整数.
(2)不是,因为任何分数的平方不可能是整数.
点评:本题主要考查无理数和勾股定理的知识点,掌握无理数的概念是解答的关键,此题是基础题,不是很难.
10、操作画图题
如图,正方形网格中的每个正方形边长都是1,每个小格的顶点叫格点,以格点为顶点,按要求画三角形:使三角形的三边长分别为3、2、(画一个即可).
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
考点:实数的运算;勾股定理。
专题:作图题;网格型。
分析:因为正方形网格中的每个正方形边长都是1,根据勾股定理可得,边长为2的正方形的对角线长2,长为2,宽为1的长方形的对角线长,然后选取一条线段,使它们能首尾相接,可得所求三角形.
解答:解:根据勾股定理可得,边长为2的正方形的对角线长2,长为2,宽为1的长方形的对角线长,
从三条线段中分别任取一条线段,使它们能首尾相接,即为所求图形.
如图:
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
点评:解决本题关键是根据勾股定理在格点图形中找出表示3,2,的线段分别有哪些.
二、填空题(共9小题)
11、两条直角边长分别是整数a,b(其中b<2011),斜边长是b+1的直角三角形的个数为 31 .
考点:完全平方数;勾股定理。
专题:计算题。
分析:先根据勾股定理得到a2=(b+1)2﹣b2=2b+1,而b是整数,b<2011,得到a2是1到4023之间的奇数,而且是完全平方数,32到632都这其中,所以a可以为3,5,…,63,由此得到满足条件的直角三角形的个数为31.
解答:解:∵两条直角边长分别是整数a,b(其中b<2011),斜边长是b+1,
∴a2=(b+1)2﹣b2=2b+1.
∴a2为奇数,
∵b是整数,b<2011,
∴a2是1到4023之间的奇数,而且是完全平方数,这样的数共有31个,即32,52,…,632.
∴a可以为3,5,…,63,
∴满足条件的直角三角形的个数为31.
故答案为:31.
点评:本题考查了完全平方数的概念.也考查了勾股定理以及会计算1~100的平方数.
12、已知直角三角形有一边是11,另两边的长度均为自然数,那么这个三角形的周长是 132 .
考点:三角形边角关系;勾股定理。
分析:设另一直角边为x,斜边为y,利用勾股定理可得y2﹣x2=121,进一步可得(y+x)(y﹣x)=121=121×1,再由x,y为自然数,即可求出x和y的值,于是三角形的周长求出.
解答:解:设另一直角边为x,斜边为y.
根据勾股定理得:
y2=x2+121,
y2﹣x2=121,
(y+x)(y﹣x)=121=121×1,
∵x,y为自然数,
∴x+y=121,y﹣x=1,
∴x=60,y=61,
∴周长为:11+61+60=132.
故答案为132.
点评:本题主要考查三角形边角关系的知识点,解答本题的关键是熟练掌握勾股定理的知识点,此题难度一般.
13、在边长为1cm的正△ABC中,P0为BC边上一点,作P0P1⊥CA于点 P1,作P1P2⊥AB于点P2,作P2P3⊥BC于点P3.如果点P3恰与点P0重合,则△P1P2P3的面积是 cm2.
考点:面积及等积变换;三角形的面积;三角形内角和定理;等边三角形的性质;含30度角的直角三角形;勾股定理。
专题:计算题。
分析:过A作AD⊥BC于D,根据等边三角形的性质和勾股定理求出BD、AD,计算三角形的面积,求出∠CP3P1=30°,推出CP3=2CP1,设CP1=a,AP2=b,BP3=c,推出CP3=2a,AP1=2b,BP2=2c,得到方程组,求出a=b=c,即可求出a、b、c,根据三角形的面积公式求出即可.
解答:解:
过A作AD⊥BC于D,
∵等边三角形ABC,
∴BD=DC=,
由勾股定理得:AD=,
∴△ABC的面积是×BC×AD=×1×=,
∵等边三角形ABC,
∴∠C=60°,
∵P3P1⊥AC,
∴∠CP3P1=30°,
∴CP3=2CP1,
设CP1=a,AP2=b,BP3=c,
∴CP3=2a,
同理AP1=2b,BP2=2c,
∴,
解得:a=b=c,
即3a=1,
∴a=b=c=,
2a=2b=2c=,
由勾股定理得:P3P1=P1P2=P2P3=,
∴△P1P2P3的面积是S△ABC﹣﹣﹣=﹣3×××=,
故答案为:.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
点评:本题主要考查对三角形的面积,三角形的内角和定理,勾股定理,面积与等积变形,等边三角形的面积,含30度角的直角三角形等知识点的理解和掌握,综合运用这些性质进行推理是解此题的关键.
14、已知直角三角形两边x,y的长满足|x2﹣4|+=0,则第三边长为 或 .
考点:非负数的性质:算术平方根;非负数的性质:绝对值;勾股定理。
专题:计算题;分类讨论。
分析:任何数的绝对值,以及算术平方根一定是非负数,已知中两个非负数的和是0,则两个一定同时是0;
另外已知直角三角形两边x、y的长,具体是两条直角边或是一条直角边一条斜边,应分类讨论.
解答:解:∵|x2﹣4|≥0,,
∴x2﹣4=0,y2﹣9=0,
∴x=2或﹣2(舍去),y=3或﹣3(舍去),
①当两直角边是2和3时,三角形是直角三角形,则斜边的长为:=;
②当2为直角边,3为斜边时,则第三边是直角边为=.
故答案为:或.
点评:本题考查了有理数加法法则,非负数的性质,另外考查勾股定理的应用,熟练掌握上述性质是解答本题的关键.
15、如图,正方形BCDE和ABFG的边长分别为2a,a,连接CE和CG,则图中阴影部分的面积是 ;CE和CG的大小关系 CE<CG .
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
考点:面积及等积变换;三角形的面积;勾股定理。
专题:计算题。
分析:(1)首先分别求出正方形ABFG、△AGC、△BEC的面积,利用S=S正方形ABFG+S△BCE﹣S△AGC,即可求出阴影部分的面积;
(2)利用勾股定理求出CE、CG的长比较即可.
解答:解:(1)设图中阴影部分的面积是S,
则:S=S正方形ABFG+S△BCE﹣S△AGC,
∵S正方形ABFG=a×a=a2,
S△BCE= 2a 2a=2a2,
S△AGC=(a+2a) a=a2,
∴S=a2+2a2﹣a2=a2.
(2)在Rt△AGC和Rt△BEC中,由勾股定理得:
CE==a,
CG==a,
∴CE<CG.
故答案为:a2,CE<CG.
点评:本题主要考查了三角形的面积公式,面积和等积变换,勾股定理等知识点,找出S=S正方形ABFG+S△BCE﹣S△AGC是解此题的关键.
16、(2008 荆门)如图,半圆的直径AB= .
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
考点:实数与数轴;勾股定理。
专题:数形结合。
分析:由图可知OE与OD、AC的长,再由勾股定理可得圆的半径OC的大小,进而可得半圆的直径AB的值.
解答:解:连接OC,
由图可知:OD=CD=1,
由勾股定理可知,OC===,
故半圆的直径为2,
故答案为.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
点评:此题很简单,解答此题关键是熟知勾股定理,理解题意.
17、如图,以数轴的单位长线段为边作一个正方形,以数轴的原点为旋转中心,将过原点的对角线顺时针旋转,使对角线的另一端点落在数轴正半轴的点A处,则点A表示的数是 .
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
考点:实数与数轴;勾股定理。
分析:根据勾股定理求出边长为1的正方形的对角线的长,再根据旋转的性质求出A点的数.
解答:解:对角线的长:,根据旋转前后线段的长分别相等,∴A点表示的数=对角线的长=.
点评:本题考查旋转的性质.旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变.
18、如图,以数轴的单位长线段为边作两个正方形,以数轴的原点为圆心,矩形对角线为半径画弧,交数轴负半轴于点A,则在数轴上A表示的数是 ﹣ .
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
考点:实数与数轴;勾股定理。
分析:根据勾股定理计算OA的长度,再由点A的位置,确定点A的符号,从而得出点A的坐标即可.
解答:解:如图:连接MB,
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
在数轴上A表示的数是﹣.
点评:本题考查了勾股定理和数轴的应用.
19、如图,数轴上点A表示的数据为 ﹣ .
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
考点:实数与数轴;勾股定理。
分析:根据数轴得出矩形的长和宽,利用勾股定理求出其对角线.
解答:解:OB==,
故数轴上点A表示的数据为﹣.
点评:本题主要考查了数轴与勾股定理的应用.
三、选择题(共11小题)
20、张大爷离家出门散步,他先向正东走了30m,接着又向正南走了40m,此时他离家的距离为( )
A、30m B、40m
C、50m D、70m
考点:正数和负数;勾股定理。
专题:计算题。
分析:根据勾股定理直接求得斜边,即为他离家的距离.
解答:解:=50m,
故选C.
点评:本题考查了正数和负数的意义以及勾股定理的运用,题目比较简单.
21、如图,已知矩形A′BOC的边长A′B=2,OB=1,数轴上点A表示的数为x,则x2﹣13的立方根是( ) ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、﹣13 B、﹣﹣13
C、2 D、﹣2
考点:立方根;实数与数轴;勾股定理。
分析:先将原式x2﹣13变形为x2﹣4﹣9,整体求出x2﹣4的值,然后根据立方根的定义来解答.
解答:解:根据勾股定理x2﹣22=12,即x2﹣22=1,
∴x2﹣13=x2﹣4﹣9=1﹣9=﹣8,
则x2﹣13的立方根是=﹣2.
故选D.
点评:本题综合性较强,不仅要结合图形,还需要熟悉勾股定理和立方根的定义.
22、如图,以数轴的单位长线段为边作一个正方形,以数轴的原点为旋转中心,将过原点的对角线顺时针旋转,使对角线的另一端点落在数轴正半轴的点A处,则点A表示的数是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、 B、1.4
C、 D、
考点:实数与数轴;勾股定理。
分析:先根据勾股定理求出正方形的对角线长,再根据两点间的距离公式即可求出A点的坐标.
解答:解:数轴上正方形的对角线长为:=,由图中可知0和A之间的距离为.
∴点A表示的数是.
故选D.
点评:本题考查的是勾股定理及两点间的距离公式,解答此题时要注意,确定点A的符号后,点A所表示的数是距离原点的距离.
23、如图,以数轴的单位长度线段为边作一个正方形,以表示数1的点为圆心,正方形对角线长为半径画弧,交数轴于点A,则点A表示的数是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、 B、﹣1+
C、﹣1 D、1
考点:实数与数轴;勾股定理。
分析:先根据勾股定理求出正方形的对角线长,再根据两点间的距离公式为:两点间的距离=较大的数﹣较小的数,便可求出1和A之间的距离,进而可求出点A表示的数.
解答:解:数轴上正方形的对角线长为:=,由图中可知1和A之间的距离为.
∴点A表示的数是1﹣.
故选D.
点评:本题考查的是勾股定理及两点间的距离公式,本题需注意:知道数轴上两点间的距离,求较小的数,就用较大的数减去两点间的距离.
24、如图,正方形OABC的边长为1,以A为圆心,AC为半径画弧,与数轴的一个交点是D,则D点表示的数为( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、 B、
C、 D、
考点:实数与数轴;勾股定理。
分析:从图上可看出AC和AD的长度相等,且在负半轴上,从而可表示出数.
解答:解:AC==,由于在原点的左边,所以点D表示的数为1﹣.
故选A.
点评:本题考查实数与数轴的知识点,以及勾股定理的应用.
25、(2004 广州)如图,在△ABC中,三边a,b,c的大小关系是( ) ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、a<b<c B、c<a<b
C、c<b<a D、b<a<c
考点:实数大小比较;勾股定理。
专题:网格型。
分析:先分析出a、b、c三边所在的直角三角形,再根据勾股定理求出三边的长,进行比较即可.
解答:解:根据勾股定理,得a==;b==;c==.
∵5<10<13,∴b<a<c.
故选D.
点评:本题考查了勾股定理及比较无理数的大小,属中学阶段的基础题目.
26、(2010 贵港)如图所示,A(﹣,0)、B(0,1)分别为x轴、y轴上的点,△ABC为等边三角形,点P(3,a)在第一象限内,且满足2S△ABP=S△ABC,则a的值为( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、 B、
C、 D、2
考点:坐标与图形性质;等边三角形的性质;勾股定理。
分析:过P点作PD⊥x轴,垂足为D,根据A(﹣,0)、B(0,1)求OA、OB,利用勾股定理求AB,可得△ABC的面积,利用
S△ABP=S△AOB+S梯形BODP﹣S△ADP,列方程求a.
解答:解:过P点作PD⊥x轴,垂足为D,
由A(﹣,0)、B(0,1),得OA=,OB=1,
由勾股定理,得AB==2
∴S△ABC=×2×=,
又S△ABP=S△AOB+S梯形BODP﹣S△ADP
=××1+×(1+a)×3﹣×(+3)×a,
=,
由2S△ABP=S△ABC,得=,
∴a=.
故选C.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
点评:本题考查了点的坐标与线段长的关系,不规则三角形面积的表示方法.
27、已知等边△ABC,点A在坐标原点,B点的坐标为(6,0),则点C的坐标为( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、(3,3) B、(3,2)
C、(2,3) D、(3,3)
考点:坐标与图形性质;等边三角形的性质;勾股定理。
分析:过C点作x轴的垂线,求出C点到两坐标轴的距离.再根据点所在象限写出坐标.
解答:解:过C点作x轴的垂线,D点为垂足.
则AD=3,CD==,
∴D(3,).
故选D.
点评:等边三角形的性质要熟练掌握.求点的坐标转化为求此点到两坐标轴的距离,注意点所在的象限.
28、如图,点A在双曲线y=上,且OA=4cm,过A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于B,则△ABC的周长为( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、cm B、5cm
C、cm D、cm
考点:反比例函数系数k的几何意义;线段垂直平分线的性质;勾股定理。
分析:根据线段垂直平分线的性质可知AB=OB,由此推出△ABC的周长=OC+AC,设OC=a,AC=b,根据勾股定理和函数解析式即可得到关于a、b的方程组,解之即可求出△ABC的周长.
解答:解:∵OA的垂直平分线交OC于B, ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
∴AB=OB,
∴△ABC的周长=OC+AC,
设OC=a,AC=b,
则:,
解得a+b=2,
即△ABC的周长=OC+AC=2.
故选A.
点评:本题考查反比例函数图象性质和线段中垂线性质,以及勾股定理的综合应用,关键是一个转换思想,即把求△ABC的周长转换成求OC+AC即可解决问题.
29、如图,带阴影的矩形面积是( )平方厘米.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、9 B、24
C、45 D、51
考点:几何体的表面积;勾股定理。
分析:根据勾股定理先求出直角边的长度,再根据长方形的面积公式求出带阴影的矩形面积.
解答:解:∵=15厘米,
∴带阴影的矩形面积=15×3=45平方厘米.
故选C.
点评:本题考查了勾股定理和长方形的面积公式.
30、如图,阴影部分是一个矩形,它的面积是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、5cm2 B、3cm2
C、4cm2 D、6cm2
考点:几何体的表面积;勾股定理。
分析:根据勾股定理先求出斜边的长度,再根据长方形的面积公式求出带阴影的矩形面积.
解答:解:∵=5厘米,
∴带阴影的矩形面积=5×1=5平方厘米.
故选A.
点评:本题考查了勾股定理和长方形的面积公式.
一、解答题(共10小题)
1、在△ABC中,AB=40,AC=60,以A为圆心,AB的长为半径作圆交BC边于D,若BD和DC的长均为正整数,求BC的长.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
2、周长为6,面积为整数的直角三角形是否存在?若不存在,请给出证明;若存在,请证明共有几个?
3、已知Rt△ABC的两条直角边的长a、b均为整数,且a为质数,若斜边c也是整数,求证:2(a+b+1)是完全平方数.
4、已知下面著名的“勾股定理”:在一个直角三角形中,两条直角边的平方之和等于斜边的平方.
试问:是否存在同时满足下列两个条件的直角三角形?
(1)三条边长均是正整数;
(2)一条直角边为素数(也称质数)p.若存在,请求出另一条直角边长;若不存在,请说明理由.
5、设直角三角形的两条直角边长分别为a,b,斜边长为c.若a,b,c均为整数,且c=ab﹣(a+b),求满足条件的直角三角形的个数.
6、已知直角三角形的边长是正整数,并且周长的数值等于这个三角形面积的数值,求斜边的长.
7、在一个半径为20cm的圆形铁板上,欲截取一面积最大的正方形铁板作机器零件,求正方形的边长(精确到0.1).
8、一个直角三角形的边长都是整数,它的面积和周长的数值相等.试确定这个直角三角形三边的长.
9、500多年前,数学各学派的学者都认为世界上的数只有整数和分数,直到有一天,大数学家毕达哥拉斯的一个名叫希帕索斯的学生,在研究1和2的比例中项时(若1:x=x:2,那么x叫1和2的比例中项),他怎么也想不出这个比例中项值.后来,他画了一个边长为1的正方形,设对角线为x,于是由毕达哥拉斯定理x2=12+12=2,他想x代表对角线的长,而x2=2,那么x必定是确定的数,这时他又为自己提出了几个问题:
(1)x是整数吗?为什么不是?
(2)x可能是分数吗?是,能找出来吗?不是,能说出理由吗?亲爱的同学,你能帮他解答这些问题吗?
10、操作画图题
如图,正方形网格中的每个正方形边长都是1,每个小格的顶点叫格点,以格点为顶点,按要求画三角形:使三角形的三边长分别为3、2、(画一个即可).
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
二、填空题(共9小题)
11、两条直角边长分别是整数a,b(其中b<2011),斜边长是b+1的直角三角形的个数为 _________ .
12、已知直角三角形有一边是11,另两边的长度均为自然数,那么这个三角形的周长是 _________ .
13、在边长为1cm的正△ABC中,P0为BC边上一点,作P0P1⊥CA于点 P1,作P1P2⊥AB于点P2,作P2P3⊥BC于点P3.如果点P3恰与点P0重合,则△P1P2P3的面积是 _________ cm2.
14、已知直角三角形两边x,y的长满足|x2﹣4|+=0,则第三边长为 _________ .
15、如图,正方形BCDE和ABFG的边长分别为2a,a,连接CE和CG,则图中阴影部分的面积是 _________ ;CE和CG的大小关系 _________ .
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
16、(2008 荆门)如图,半圆的直径AB= _________ .
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
17、如图,以数轴的单位长线段为边作一个正方形,以数轴的原点为旋转中心,将过原点的对角线顺时针旋转,使对角线的另一端点落在数轴正半轴的点A处,则点A表示的数是 _________ .
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
18、如图,以数轴的单位长线段为边作两个正方形,以数轴的原点为圆心,矩形对角线为半径画弧,交数轴负半轴于点A,则在数轴上A表示的数是 _________ .
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
19、如图,数轴上点A表示的数据为 _________ .
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
三、选择题(共11小题)
20、张大爷离家出门散步,他先向正东走了30m,接着又向正南走了40m,此时他离家的距离为( )
A、30m B、40m
C、50m D、70m
21、如图,已知矩形A′BOC的边长A′B=2,OB=1,数轴上点A表示的数为x,则x2﹣13的立方根是( ) ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、﹣13 B、﹣﹣13
C、2 D、﹣2
22、如图,以数轴的单位长线段为边作一个正方形,以数轴的原点为旋转中心,将过原点的对角线顺时针旋转,使对角线的另一端点落在数轴正半轴的点A处,则点A表示的数是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、 B、1.4
C、 D、
23、如图,以数轴的单位长度线段为边作一个正方形,以表示数1的点为圆心,正方形对角线长为半径画弧,交数轴于点A,则点A表示的数是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、 B、﹣1+
C、﹣1 D、1
24、如图,正方形OABC的边长为1,以A为圆心,AC为半径画弧,与数轴的一个交点是D,则D点表示的数为( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、 B、
C、 D、
25、(2004 广州)如图,在△ABC中,三边a,b,c的大小关系是( ) ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、a<b<c B、c<a<b
C、c<b<a D、b<a<c
26、(2010 贵港)如图所示,A(﹣,0)、B(0,1)分别为x轴、y轴上的点,△ABC为等边三角形,点P(3,a)在第一象限内,且满足2S△ABP=S△ABC,则a的值为( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、 B、
C、 D、2
27、已知等边△ABC,点A在坐标原点,B点的坐标为(6,0),则点C的坐标为( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、(3,3) B、(3,2)
C、(2,3) D、(3,3)
28、如图,点A在双曲线y=上,且OA=4cm,过A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于B,则△ABC的周长为( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、cm B、5cm
C、cm D、cm
29、如图,带阴影的矩形面积是( )平方厘米.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、9 B、24
C、45 D、51
30、如图,阴影部分是一个矩形,它的面积是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、5cm2 B、3cm2
C、4cm2 D、6cm2
答案与评分标准
一、解答题(共10小题)
1、在△ABC中,AB=40,AC=60,以A为圆心,AB的长为半径作圆交BC边于D,若BD和DC的长均为正整数,求BC的长.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
考点:数的整除性问题;等边三角形的性质;勾股定理。
专题:计算题。
分析:首先假设出BD,CD的长度,再利用勾股定理得出a+b与b的乘积为2000,再利用三角形三边关系得出20<a+b<100,进一步得出a+b的值.
解答:解:设BD=a,CD=b,(a,b为正整数)
作AE⊥BD,垂足为E,则AB=AD=40,BE=DE=.
∵,,
∴,
∴(a+b)b=2000=24×53,
∵20<a+b<100,
∴只有或
故BC的长为50或80.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
点评:此题主要考查了数的整除性知识,以及勾股定理的应用和三角形三边关系,题目综合性较强.
2、周长为6,面积为整数的直角三角形是否存在?若不存在,请给出证明;若存在,请证明共有几个?
考点:非一次不定方程(组);勾股定理。
专题:证明题;探究型。
分析:设存在如上的直角三角形,设两直角边分别为a,b,斜边为c,根据题意可得出关于a、b、c的方程,由勾股定理可判断出c的取值范围,进而求出c的值,把c的值代入不定方程即可求出b、c的值,找出符合条件的未知数的对应值即可.
解答:解:设存在如上的直角三角形,设两直角边分别为a,b,斜边为c,
∵a+b+c=6(1);
a2+b2=c2(2)
∴(a+b)2=(6﹣c)2(3)
∵ab=9﹣3c为整数,
∴c为整数或以3为分母的分数;
∵直角三角形斜边最长则有c>2,根据三角形三边边长规律有c<3;
∴2<c<3;
∴c应为以3为分母的分数,a=或;
当c=时,根据(1)(2)式有:b=6或,a=﹣或,不合题意.
当c=时,根据(1)(2)式有:b=,a=或a=,b=,
∴这样的直角三角形存在,恰有一个,两条直角边为与,斜边为.
点评:本题考查的是非一次不定方程及勾股定理,根据题意判断出c的值是解答此题的关键.
3、已知Rt△ABC的两条直角边的长a、b均为整数,且a为质数,若斜边c也是整数,求证:2(a+b+1)是完全平方数.
考点:完全平方数;勾股定理。
专题:证明题。
分析:由勾股定理易得a2+b2=c2,则a2=c2﹣b2=(c+b)(c﹣b),因为a为质数,所以c+b=a2,c﹣b=1,两式相减可得a2=2b+1,代入2(a+b+1)即可得证.
解答:解:∵a,b是Rt△ABC的两条直角边,c是斜边,
∴a2+b2=c2,
即a2=c2﹣b2=(c+b)(c﹣b),
∵a为质数,
∴c+b=a2,c﹣b=1,
∴a2=2b+1,
∴2(a+b+1)=a2+2a+1=(a+1)2,
∴2(a+b+1)是完全平方数.
点评:此题考查完全平方数,根据勾股定理和a为质数展开答题,是关键.
4、已知下面著名的“勾股定理”:在一个直角三角形中,两条直角边的平方之和等于斜边的平方.
试问:是否存在同时满足下列两个条件的直角三角形?
(1)三条边长均是正整数;
(2)一条直角边为素数(也称质数)p.若存在,请求出另一条直角边长;若不存在,请说明理由.
考点:质数与合数;勾股定理。
专题:计算题。
分析:首先假设存在,设另一条直角边长为x,斜边长为y,则x、y为正整数,然后根据题意可得:p2+x2=y2,即可得:(y+x)(y﹣x)=p2,又由p为素数,讨论分析即可求得.
解答:解:假设存在,令另一条直角边长为x,斜边长为y,则x、y为正整数.
由勾股定理得p2+x2=y2.
化为(y+x)(y﹣x)=p2.
因为p为素数(也称质数),且y+x>y﹣x,
所以只有
从而.
若p=2,则x、y不是整数,这样的三角形不存在;
若p为奇素数,x、y都是整数,这样的三角形存在.
综上所述,可知:p为偶素数2时,满足条件的三角形不存在;p为奇素数时,满足条件的三角形存在,且另一条直角边长为.
点评:此题考查了素数的意义和勾股定理等知识.难度较大,要注意分类讨论思想的应用.
5、设直角三角形的两条直角边长分别为a,b,斜边长为c.若a,b,c均为整数,且c=ab﹣(a+b),求满足条件的直角三角形的个数.
考点:非一次不定方程(组);勾股定理。
专题:探究型。
分析:先根据此三角形是直角三角形,利用勾股定理把原式化为(a﹣6)(b﹣6)=18,再根据a,b均为正整数,不妨设a<b,可得出关于a、b的二元一次方程,求出a、b、c的对应值即可.
解答:解:由勾股定理得,c2=a2+b2.
又∵c=ab﹣(a+b),得.
即.
整理得,ab﹣6(a+b)+18=0,即(a﹣6)(b﹣6)=18,
∵a,b均为正整数,不妨设a<b,
可得或或,
可解出或或,
∴满足条件的直角三角形有3个.
故答案为:3.
点评:本题考查的是非一次不定方程及勾股定理,解答此题的关键是先利用勾股定理把原式化为两个因式积的形式,再根据a,b均为正整数进行解答.
6、已知直角三角形的边长是正整数,并且周长的数值等于这个三角形面积的数值,求斜边的长.
考点:一元二次方程的整数根与有理根;勾股定理。
专题:计算题;分类讨论。
分析:首先根据题目设出未知数a,b,在根据勾股定理a2+b2=c2列出等式,再把其进行化简,用含a的代数式表示b,因为边长都是整数,所以分情况讨论时,取整数情况即可.
解答:解:设直角边为a,b 由题意得:
=a+b+
移项,平方并化简得到:
+2ab﹣ab(a+b)=0
∵ab≠0
∴a+b﹣=2
b===4+
∵b是正整数
∴①a=5,b=12,c=13
②a=6,b=8,c=10
③a=8,b=6,c=10
④a=12,b=5,c=13
∴符合题意的直角三角形的斜边长10或13.
点评:此题主要考查了勾股定理与求方程的整数解的综合运用,用到了数学中的分类讨论思想,注注意讨论是要考虑全面.
7、在一个半径为20cm的圆形铁板上,欲截取一面积最大的正方形铁板作机器零件,求正方形的边长(精确到0.1).
考点:平方根;勾股定理。
分析:正方形的四个顶点都正好在圆板的外沿上时,所截正方形面积最大,此时正方形的对角线为圆的直径,根据勾股定理求解即可.
解答:解:正方形的四个顶点都正好在圆板的外沿上时,所截正方形面积最大,
此时正方形的对角线应是圆的直径.设正方形的边长为xcm,
由题意,得x2+x2=402,解得x=±20(负值舍去).
∴x=20≈20×1.414=28.28≈28.3cm.
∴正方形的边长28.3cm.
点评:本题考查了平方根和勾股定理的运用,属于常见的题型,需要熟练掌握.
8、一个直角三角形的边长都是整数,它的面积和周长的数值相等.试确定这个直角三角形三边的长.
考点:三角形边角关系;勾股定理。
专题:计算题。
分析:设符合条件的直角三角形的三边长为a、b、c,其中c为斜边,则a2+b2=c2,a+b+c=,于是将存在性问题的讨论转化为求方程组的解.
解答:解:假设符合条件的直角三角形存在,它的三边长为a、b、c,其中c为斜边,则
a2+b2=c2,a+b+c=,
∵a、b、c均为正整数,
∴a≠b;不妨设a>b,则有a+b+=,
两边平方,并整理得,
﹣a2b﹣ab2+2ab=0,
消去ab,得
﹣a﹣b+2=0,即(a﹣4)(b﹣4)=8,
又∵8=1×8=2×4,
∴①a﹣4=8,b﹣4=1,解得:a=12,b=5,则c=13;
②a﹣4=4,b﹣4=2,解得:a=8,b=6,则c=10;
综上所述,符合条件的直角三角形的边长分别是5、12、13;6、8、10.
点评:本题主要考查了一元二次方程的整数根及有理根、勾股定理的逆定理的应用.在解题过程中,当勾股定理不能直接运用时,常需要通过等线段的代换、作辅助垂线等途径,为勾股定理的运用创造必要的条件,有时又需要由线段的数量关系去判断线段的位置关系,这就需要熟悉一些常用的勾股数组.
9、500多年前,数学各学派的学者都认为世界上的数只有整数和分数,直到有一天,大数学家毕达哥拉斯的一个名叫希帕索斯的学生,在研究1和2的比例中项时(若1:x=x:2,那么x叫1和2的比例中项),他怎么也想不出这个比例中项值.后来,他画了一个边长为1的正方形,设对角线为x,于是由毕达哥拉斯定理x2=12+12=2,他想x代表对角线的长,而x2=2,那么x必定是确定的数,这时他又为自己提出了几个问题:
(1)x是整数吗?为什么不是?
(2)x可能是分数吗?是,能找出来吗?不是,能说出理由吗?亲爱的同学,你能帮他解答这些问题吗?
考点:无理数;勾股定理。
专题:常规题型。
分析:(1)根据比例中项的定义,可知x2=2,结合无理数的概念,就能得出x是不是整数的结论.
(2)根据分数的定义,任何分数的平方还是分数,即能得出结论.
解答:解:(1)不是,∵1<2<4,而x2=2
∴1<x2<4,若x>0,1<x<2,
∴在1和2之间不存在另外的整数.
(2)不是,因为任何分数的平方不可能是整数.
点评:本题主要考查无理数和勾股定理的知识点,掌握无理数的概念是解答的关键,此题是基础题,不是很难.
10、操作画图题
如图,正方形网格中的每个正方形边长都是1,每个小格的顶点叫格点,以格点为顶点,按要求画三角形:使三角形的三边长分别为3、2、(画一个即可).
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
考点:实数的运算;勾股定理。
专题:作图题;网格型。
分析:因为正方形网格中的每个正方形边长都是1,根据勾股定理可得,边长为2的正方形的对角线长2,长为2,宽为1的长方形的对角线长,然后选取一条线段,使它们能首尾相接,可得所求三角形.
解答:解:根据勾股定理可得,边长为2的正方形的对角线长2,长为2,宽为1的长方形的对角线长,
从三条线段中分别任取一条线段,使它们能首尾相接,即为所求图形.
如图:
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
点评:解决本题关键是根据勾股定理在格点图形中找出表示3,2,的线段分别有哪些.
二、填空题(共9小题)
11、两条直角边长分别是整数a,b(其中b<2011),斜边长是b+1的直角三角形的个数为 31 .
考点:完全平方数;勾股定理。
专题:计算题。
分析:先根据勾股定理得到a2=(b+1)2﹣b2=2b+1,而b是整数,b<2011,得到a2是1到4023之间的奇数,而且是完全平方数,32到632都这其中,所以a可以为3,5,…,63,由此得到满足条件的直角三角形的个数为31.
解答:解:∵两条直角边长分别是整数a,b(其中b<2011),斜边长是b+1,
∴a2=(b+1)2﹣b2=2b+1.
∴a2为奇数,
∵b是整数,b<2011,
∴a2是1到4023之间的奇数,而且是完全平方数,这样的数共有31个,即32,52,…,632.
∴a可以为3,5,…,63,
∴满足条件的直角三角形的个数为31.
故答案为:31.
点评:本题考查了完全平方数的概念.也考查了勾股定理以及会计算1~100的平方数.
12、已知直角三角形有一边是11,另两边的长度均为自然数,那么这个三角形的周长是 132 .
考点:三角形边角关系;勾股定理。
分析:设另一直角边为x,斜边为y,利用勾股定理可得y2﹣x2=121,进一步可得(y+x)(y﹣x)=121=121×1,再由x,y为自然数,即可求出x和y的值,于是三角形的周长求出.
解答:解:设另一直角边为x,斜边为y.
根据勾股定理得:
y2=x2+121,
y2﹣x2=121,
(y+x)(y﹣x)=121=121×1,
∵x,y为自然数,
∴x+y=121,y﹣x=1,
∴x=60,y=61,
∴周长为:11+61+60=132.
故答案为132.
点评:本题主要考查三角形边角关系的知识点,解答本题的关键是熟练掌握勾股定理的知识点,此题难度一般.
13、在边长为1cm的正△ABC中,P0为BC边上一点,作P0P1⊥CA于点 P1,作P1P2⊥AB于点P2,作P2P3⊥BC于点P3.如果点P3恰与点P0重合,则△P1P2P3的面积是 cm2.
考点:面积及等积变换;三角形的面积;三角形内角和定理;等边三角形的性质;含30度角的直角三角形;勾股定理。
专题:计算题。
分析:过A作AD⊥BC于D,根据等边三角形的性质和勾股定理求出BD、AD,计算三角形的面积,求出∠CP3P1=30°,推出CP3=2CP1,设CP1=a,AP2=b,BP3=c,推出CP3=2a,AP1=2b,BP2=2c,得到方程组,求出a=b=c,即可求出a、b、c,根据三角形的面积公式求出即可.
解答:解:
过A作AD⊥BC于D,
∵等边三角形ABC,
∴BD=DC=,
由勾股定理得:AD=,
∴△ABC的面积是×BC×AD=×1×=,
∵等边三角形ABC,
∴∠C=60°,
∵P3P1⊥AC,
∴∠CP3P1=30°,
∴CP3=2CP1,
设CP1=a,AP2=b,BP3=c,
∴CP3=2a,
同理AP1=2b,BP2=2c,
∴,
解得:a=b=c,
即3a=1,
∴a=b=c=,
2a=2b=2c=,
由勾股定理得:P3P1=P1P2=P2P3=,
∴△P1P2P3的面积是S△ABC﹣﹣﹣=﹣3×××=,
故答案为:.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
点评:本题主要考查对三角形的面积,三角形的内角和定理,勾股定理,面积与等积变形,等边三角形的面积,含30度角的直角三角形等知识点的理解和掌握,综合运用这些性质进行推理是解此题的关键.
14、已知直角三角形两边x,y的长满足|x2﹣4|+=0,则第三边长为 或 .
考点:非负数的性质:算术平方根;非负数的性质:绝对值;勾股定理。
专题:计算题;分类讨论。
分析:任何数的绝对值,以及算术平方根一定是非负数,已知中两个非负数的和是0,则两个一定同时是0;
另外已知直角三角形两边x、y的长,具体是两条直角边或是一条直角边一条斜边,应分类讨论.
解答:解:∵|x2﹣4|≥0,,
∴x2﹣4=0,y2﹣9=0,
∴x=2或﹣2(舍去),y=3或﹣3(舍去),
①当两直角边是2和3时,三角形是直角三角形,则斜边的长为:=;
②当2为直角边,3为斜边时,则第三边是直角边为=.
故答案为:或.
点评:本题考查了有理数加法法则,非负数的性质,另外考查勾股定理的应用,熟练掌握上述性质是解答本题的关键.
15、如图,正方形BCDE和ABFG的边长分别为2a,a,连接CE和CG,则图中阴影部分的面积是 ;CE和CG的大小关系 CE<CG .
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
考点:面积及等积变换;三角形的面积;勾股定理。
专题:计算题。
分析:(1)首先分别求出正方形ABFG、△AGC、△BEC的面积,利用S=S正方形ABFG+S△BCE﹣S△AGC,即可求出阴影部分的面积;
(2)利用勾股定理求出CE、CG的长比较即可.
解答:解:(1)设图中阴影部分的面积是S,
则:S=S正方形ABFG+S△BCE﹣S△AGC,
∵S正方形ABFG=a×a=a2,
S△BCE= 2a 2a=2a2,
S△AGC=(a+2a) a=a2,
∴S=a2+2a2﹣a2=a2.
(2)在Rt△AGC和Rt△BEC中,由勾股定理得:
CE==a,
CG==a,
∴CE<CG.
故答案为:a2,CE<CG.
点评:本题主要考查了三角形的面积公式,面积和等积变换,勾股定理等知识点,找出S=S正方形ABFG+S△BCE﹣S△AGC是解此题的关键.
16、(2008 荆门)如图,半圆的直径AB= .
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
考点:实数与数轴;勾股定理。
专题:数形结合。
分析:由图可知OE与OD、AC的长,再由勾股定理可得圆的半径OC的大小,进而可得半圆的直径AB的值.
解答:解:连接OC,
由图可知:OD=CD=1,
由勾股定理可知,OC===,
故半圆的直径为2,
故答案为.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
点评:此题很简单,解答此题关键是熟知勾股定理,理解题意.
17、如图,以数轴的单位长线段为边作一个正方形,以数轴的原点为旋转中心,将过原点的对角线顺时针旋转,使对角线的另一端点落在数轴正半轴的点A处,则点A表示的数是 .
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
考点:实数与数轴;勾股定理。
分析:根据勾股定理求出边长为1的正方形的对角线的长,再根据旋转的性质求出A点的数.
解答:解:对角线的长:,根据旋转前后线段的长分别相等,∴A点表示的数=对角线的长=.
点评:本题考查旋转的性质.旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变.
18、如图,以数轴的单位长线段为边作两个正方形,以数轴的原点为圆心,矩形对角线为半径画弧,交数轴负半轴于点A,则在数轴上A表示的数是 ﹣ .
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
考点:实数与数轴;勾股定理。
分析:根据勾股定理计算OA的长度,再由点A的位置,确定点A的符号,从而得出点A的坐标即可.
解答:解:如图:连接MB,
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
在数轴上A表示的数是﹣.
点评:本题考查了勾股定理和数轴的应用.
19、如图,数轴上点A表示的数据为 ﹣ .
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
考点:实数与数轴;勾股定理。
分析:根据数轴得出矩形的长和宽,利用勾股定理求出其对角线.
解答:解:OB==,
故数轴上点A表示的数据为﹣.
点评:本题主要考查了数轴与勾股定理的应用.
三、选择题(共11小题)
20、张大爷离家出门散步,他先向正东走了30m,接着又向正南走了40m,此时他离家的距离为( )
A、30m B、40m
C、50m D、70m
考点:正数和负数;勾股定理。
专题:计算题。
分析:根据勾股定理直接求得斜边,即为他离家的距离.
解答:解:=50m,
故选C.
点评:本题考查了正数和负数的意义以及勾股定理的运用,题目比较简单.
21、如图,已知矩形A′BOC的边长A′B=2,OB=1,数轴上点A表示的数为x,则x2﹣13的立方根是( ) ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、﹣13 B、﹣﹣13
C、2 D、﹣2
考点:立方根;实数与数轴;勾股定理。
分析:先将原式x2﹣13变形为x2﹣4﹣9,整体求出x2﹣4的值,然后根据立方根的定义来解答.
解答:解:根据勾股定理x2﹣22=12,即x2﹣22=1,
∴x2﹣13=x2﹣4﹣9=1﹣9=﹣8,
则x2﹣13的立方根是=﹣2.
故选D.
点评:本题综合性较强,不仅要结合图形,还需要熟悉勾股定理和立方根的定义.
22、如图,以数轴的单位长线段为边作一个正方形,以数轴的原点为旋转中心,将过原点的对角线顺时针旋转,使对角线的另一端点落在数轴正半轴的点A处,则点A表示的数是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、 B、1.4
C、 D、
考点:实数与数轴;勾股定理。
分析:先根据勾股定理求出正方形的对角线长,再根据两点间的距离公式即可求出A点的坐标.
解答:解:数轴上正方形的对角线长为:=,由图中可知0和A之间的距离为.
∴点A表示的数是.
故选D.
点评:本题考查的是勾股定理及两点间的距离公式,解答此题时要注意,确定点A的符号后,点A所表示的数是距离原点的距离.
23、如图,以数轴的单位长度线段为边作一个正方形,以表示数1的点为圆心,正方形对角线长为半径画弧,交数轴于点A,则点A表示的数是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、 B、﹣1+
C、﹣1 D、1
考点:实数与数轴;勾股定理。
分析:先根据勾股定理求出正方形的对角线长,再根据两点间的距离公式为:两点间的距离=较大的数﹣较小的数,便可求出1和A之间的距离,进而可求出点A表示的数.
解答:解:数轴上正方形的对角线长为:=,由图中可知1和A之间的距离为.
∴点A表示的数是1﹣.
故选D.
点评:本题考查的是勾股定理及两点间的距离公式,本题需注意:知道数轴上两点间的距离,求较小的数,就用较大的数减去两点间的距离.
24、如图,正方形OABC的边长为1,以A为圆心,AC为半径画弧,与数轴的一个交点是D,则D点表示的数为( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、 B、
C、 D、
考点:实数与数轴;勾股定理。
分析:从图上可看出AC和AD的长度相等,且在负半轴上,从而可表示出数.
解答:解:AC==,由于在原点的左边,所以点D表示的数为1﹣.
故选A.
点评:本题考查实数与数轴的知识点,以及勾股定理的应用.
25、(2004 广州)如图,在△ABC中,三边a,b,c的大小关系是( ) ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、a<b<c B、c<a<b
C、c<b<a D、b<a<c
考点:实数大小比较;勾股定理。
专题:网格型。
分析:先分析出a、b、c三边所在的直角三角形,再根据勾股定理求出三边的长,进行比较即可.
解答:解:根据勾股定理,得a==;b==;c==.
∵5<10<13,∴b<a<c.
故选D.
点评:本题考查了勾股定理及比较无理数的大小,属中学阶段的基础题目.
26、(2010 贵港)如图所示,A(﹣,0)、B(0,1)分别为x轴、y轴上的点,△ABC为等边三角形,点P(3,a)在第一象限内,且满足2S△ABP=S△ABC,则a的值为( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、 B、
C、 D、2
考点:坐标与图形性质;等边三角形的性质;勾股定理。
分析:过P点作PD⊥x轴,垂足为D,根据A(﹣,0)、B(0,1)求OA、OB,利用勾股定理求AB,可得△ABC的面积,利用
S△ABP=S△AOB+S梯形BODP﹣S△ADP,列方程求a.
解答:解:过P点作PD⊥x轴,垂足为D,
由A(﹣,0)、B(0,1),得OA=,OB=1,
由勾股定理,得AB==2
∴S△ABC=×2×=,
又S△ABP=S△AOB+S梯形BODP﹣S△ADP
=××1+×(1+a)×3﹣×(+3)×a,
=,
由2S△ABP=S△ABC,得=,
∴a=.
故选C.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
点评:本题考查了点的坐标与线段长的关系,不规则三角形面积的表示方法.
27、已知等边△ABC,点A在坐标原点,B点的坐标为(6,0),则点C的坐标为( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、(3,3) B、(3,2)
C、(2,3) D、(3,3)
考点:坐标与图形性质;等边三角形的性质;勾股定理。
分析:过C点作x轴的垂线,求出C点到两坐标轴的距离.再根据点所在象限写出坐标.
解答:解:过C点作x轴的垂线,D点为垂足.
则AD=3,CD==,
∴D(3,).
故选D.
点评:等边三角形的性质要熟练掌握.求点的坐标转化为求此点到两坐标轴的距离,注意点所在的象限.
28、如图,点A在双曲线y=上,且OA=4cm,过A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于B,则△ABC的周长为( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、cm B、5cm
C、cm D、cm
考点:反比例函数系数k的几何意义;线段垂直平分线的性质;勾股定理。
分析:根据线段垂直平分线的性质可知AB=OB,由此推出△ABC的周长=OC+AC,设OC=a,AC=b,根据勾股定理和函数解析式即可得到关于a、b的方程组,解之即可求出△ABC的周长.
解答:解:∵OA的垂直平分线交OC于B, ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
∴AB=OB,
∴△ABC的周长=OC+AC,
设OC=a,AC=b,
则:,
解得a+b=2,
即△ABC的周长=OC+AC=2.
故选A.
点评:本题考查反比例函数图象性质和线段中垂线性质,以及勾股定理的综合应用,关键是一个转换思想,即把求△ABC的周长转换成求OC+AC即可解决问题.
29、如图,带阴影的矩形面积是( )平方厘米.
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、9 B、24
C、45 D、51
考点:几何体的表面积;勾股定理。
分析:根据勾股定理先求出直角边的长度,再根据长方形的面积公式求出带阴影的矩形面积.
解答:解:∵=15厘米,
∴带阴影的矩形面积=15×3=45平方厘米.
故选C.
点评:本题考查了勾股定理和长方形的面积公式.
30、如图,阴影部分是一个矩形,它的面积是( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A、5cm2 B、3cm2
C、4cm2 D、6cm2
考点:几何体的表面积;勾股定理。
分析:根据勾股定理先求出斜边的长度,再根据长方形的面积公式求出带阴影的矩形面积.
解答:解:∵=5厘米,
∴带阴影的矩形面积=5×1=5平方厘米.
故选A.
点评:本题考查了勾股定理和长方形的面积公式.
