人教版数学九年级上册 24.1《圆的有关性质》(第4课时)课件(共16张PPT)
文档属性
| 名称 | 人教版数学九年级上册 24.1《圆的有关性质》(第4课时)课件(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 136.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-17 08:35:57 | ||
图片预览




文档简介
(共17张PPT)
24.1 圆的有关性质(第4课时)
九年级 上册
本课是在学习了垂径定理、圆心角及弧、弦、圆心角的关系的基础上探究同弧(或等弧)所对圆周角之间以及圆周角与圆心角之间的数量关系.
课件说明
学习目标: 1.了解并证明圆周角定理及其推论; 2.经历探究同弧(或等弧)所对圆周角与圆心角之 间的关系的过程,进一步体会分类讨论、转化的 思想方法.
学习重点: 圆周角定理.
课件说明
1.思考和练习
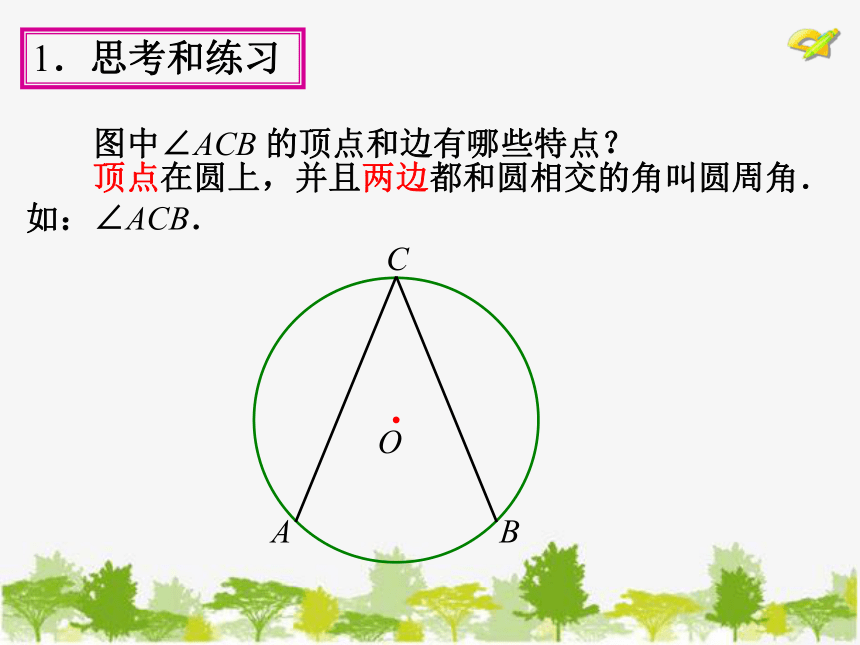
图中∠ACB 的顶点和边有哪些特点?
A
O
B
C
顶点在圆上,并且两边都和圆相交的角叫圆周角.
如:∠ACB.
教科书 88 页 练习 1.
1.思考和练习
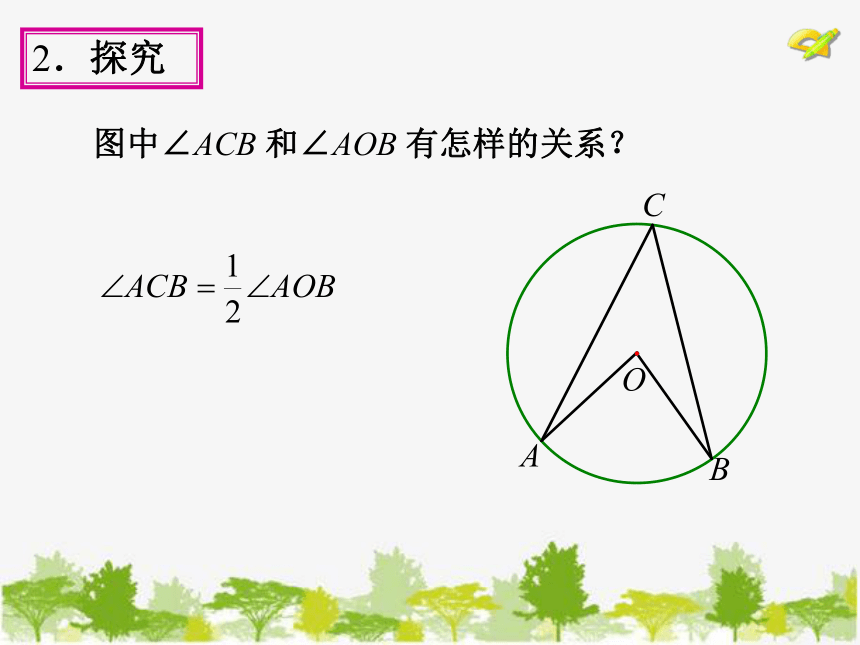
图中∠ACB 和∠AOB 有怎样的关系?
2.探究
B
C
O
A
2.探究
B
C
O
A
B
C
O
A
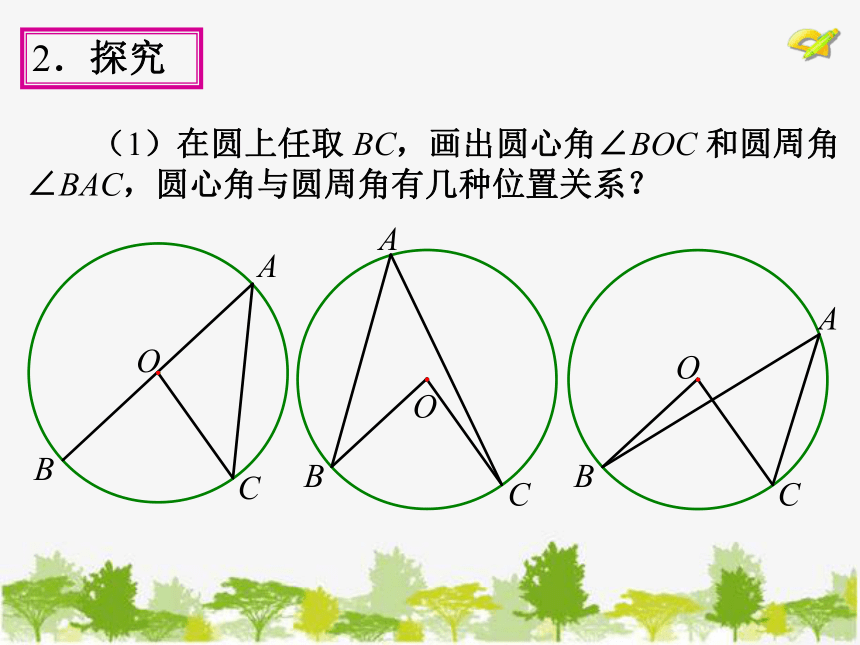
(1)在圆上任取 ,画出圆心角∠BOC 和圆周角∠BAC,圆心角与圆周角有几种位置关系?
BC
B
C
O
A
(2)如图,如何证明一条弧所对的圆周角等于它 所对的圆心角的一半?
3.证明猜想
B
C
O
A
∵ OA=OC,
∴ ∠A=∠C. 又∵ ∠BOC=∠A+∠C,
∴
我们来分析上页的前两种情况,第三种情况请同学们完成证明.
(3)如图,如何证明一条弧所对的圆周角等于它 所对的圆心角的一半?
D
3.证明猜想
B
C
O
A
证明:如图,连接 AO 并延长交⊙O 于点 D.
∵ OA=OB,
∴ ∠BAD=∠B. 又∵ ∠BOD=∠BAD+∠B,
∴
同理,
∴
3.证明猜想
圆周角定理:
一条弧所对的圆周角等于它所对的圆心角的一半.
思考:
一条弧所对的圆周角之间有什么关系?同弧或等弧 所对的圆周角之间有什么关系?
同弧或等弧所对的圆周角相等.
4.探究
A
D
B
C
O
思考:
半圆(或直径)所对的圆周角有什么特殊性?
半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
4.探究
C1
A
O
B
C2
C3
如图,⊙O 的直径 AB 为 10 cm,弦 AC 为 6 cm, ACB 的平分线交⊙O 于点 D,求 BC,AD,BD 的长.
5.应用
解:连接 OD,AD,BD,
A
C
B
D
O
∵ AB 是⊙O 的直径,
∴ ACB= ADB=90°.
在 Rt△ABC 中,
BC= = =8(cm)
如图,⊙O 的直径 AB 为 10 cm,弦 AC 为 6 cm, ACB 的平分线交⊙O 于点 D,求 BC,AD,BD 的长.
5.应用
A
C
B
D
O
∵ CD 平分 ACB,
∴ ACD= BCD,
∴ AOD= BOD .
∴ AD=BD.
在 Rt△ABD 中,
AD2+BD2=AB2 ,
∴ AD=BD=
= (cm).
(1)本节课学习了哪些主要内容?
(2)我们是怎样探究圆周角定理的?在证明过程 中用到了哪些思想方法?
6.课堂小结
教科书第 88 页 练习第 2,3,4 题.
7.布置作业
24.1 圆的有关性质(第4课时)
九年级 上册
本课是在学习了垂径定理、圆心角及弧、弦、圆心角的关系的基础上探究同弧(或等弧)所对圆周角之间以及圆周角与圆心角之间的数量关系.
课件说明
学习目标: 1.了解并证明圆周角定理及其推论; 2.经历探究同弧(或等弧)所对圆周角与圆心角之 间的关系的过程,进一步体会分类讨论、转化的 思想方法.
学习重点: 圆周角定理.
课件说明
1.思考和练习
图中∠ACB 的顶点和边有哪些特点?
A
O
B
C
顶点在圆上,并且两边都和圆相交的角叫圆周角.
如:∠ACB.
教科书 88 页 练习 1.
1.思考和练习
图中∠ACB 和∠AOB 有怎样的关系?
2.探究
B
C
O
A
2.探究
B
C
O
A
B
C
O
A
(1)在圆上任取 ,画出圆心角∠BOC 和圆周角∠BAC,圆心角与圆周角有几种位置关系?
BC
B
C
O
A
(2)如图,如何证明一条弧所对的圆周角等于它 所对的圆心角的一半?
3.证明猜想
B
C
O
A
∵ OA=OC,
∴ ∠A=∠C. 又∵ ∠BOC=∠A+∠C,
∴
我们来分析上页的前两种情况,第三种情况请同学们完成证明.
(3)如图,如何证明一条弧所对的圆周角等于它 所对的圆心角的一半?
D
3.证明猜想
B
C
O
A
证明:如图,连接 AO 并延长交⊙O 于点 D.
∵ OA=OB,
∴ ∠BAD=∠B. 又∵ ∠BOD=∠BAD+∠B,
∴
同理,
∴
3.证明猜想
圆周角定理:
一条弧所对的圆周角等于它所对的圆心角的一半.
思考:
一条弧所对的圆周角之间有什么关系?同弧或等弧 所对的圆周角之间有什么关系?
同弧或等弧所对的圆周角相等.
4.探究
A
D
B
C
O
思考:
半圆(或直径)所对的圆周角有什么特殊性?
半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
4.探究
C1
A
O
B
C2
C3
如图,⊙O 的直径 AB 为 10 cm,弦 AC 为 6 cm, ACB 的平分线交⊙O 于点 D,求 BC,AD,BD 的长.
5.应用
解:连接 OD,AD,BD,
A
C
B
D
O
∵ AB 是⊙O 的直径,
∴ ACB= ADB=90°.
在 Rt△ABC 中,
BC= = =8(cm)
如图,⊙O 的直径 AB 为 10 cm,弦 AC 为 6 cm, ACB 的平分线交⊙O 于点 D,求 BC,AD,BD 的长.
5.应用
A
C
B
D
O
∵ CD 平分 ACB,
∴ ACD= BCD,
∴ AOD= BOD .
∴ AD=BD.
在 Rt△ABD 中,
AD2+BD2=AB2 ,
∴ AD=BD=
= (cm).
(1)本节课学习了哪些主要内容?
(2)我们是怎样探究圆周角定理的?在证明过程 中用到了哪些思想方法?
6.课堂小结
教科书第 88 页 练习第 2,3,4 题.
7.布置作业
同课章节目录
