沪科版数学七年级下册 第10章 相交线、平行线与平移单元测试(word版含答案)
文档属性
| 名称 | 沪科版数学七年级下册 第10章 相交线、平行线与平移单元测试(word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 13.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-17 10:08:57 | ||
图片预览


文档简介
第10章 相交线、平行线与平移
(时间:90分钟 满分:100分)
一、选择题(每小题3分,共30分)
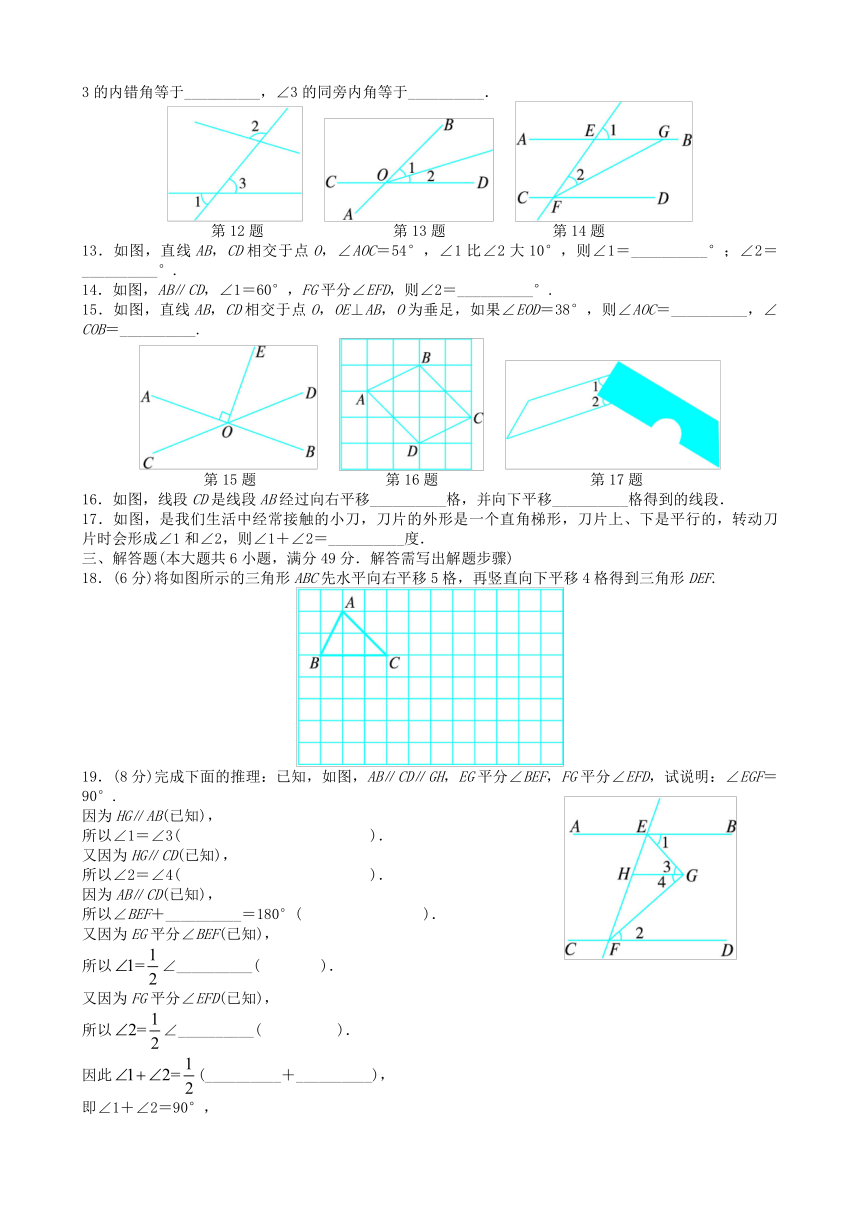
1.下列说法中正确的是( ).
A.有且只有一条直线垂直于已知直线
B.互相垂直的两条线段一定相交
C.从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离
D.直线c外一点A与直线c上各点连接而成的所有线段中,最短的线段长是3 cm,则点A到直线c的距离是3 cm
2.在下图右侧的四个三角形中,能由△ABC经过平移得到的是( ).
3.如图,下列说法错误的是( ).
A.∠A与∠C是同旁内角 B.∠1与∠3是同位角
C.∠2与∠3是内错角 D.∠3与∠B是同旁内角
第3题 第4题 第5题
4.如图,直线AB,CD相交于点O,OE⊥CD于点O,∠AOC=36°,则∠BOE=( ).
A.36° B.64° C.144° D.54°
5.如图,直线a,b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°.其中能判断a∥b的条件是( ).
A.①③ B.②④ C.①③④ D.①②③④
6.已知OA⊥OC,∠AOB∶∠AOC=2∶3,则∠BOC的度数为( ).
A.30° B.150° C.30°或150° D.不同于以上答案
7.如图,AB∥CD,∠DCE=80°,则∠BEF=( ).
A.120° B.110° C.100° D.80°
第7题 第8题 第9题 第10题
8.如图,AB⊥BC,BC⊥CD,∠EBC=∠BCF,那么∠ABE与∠DCF的位置和大小关系是( ).
A.是同位角且相等 B.不是同位角但相等
C.是同位角但不等 D.不是同位角也不等
9.如图,一条公路修到湖边时,需拐弯绕湖而过,如果第一次拐的角∠A是120°,第二次拐的角∠B是150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C是( ).
A.120° B.130° C.140° D.150°
10.如图,已知AB∥CD,AD∥BC,∠ABE是平角,则下列说法中正确的是( ).
A.∠1=∠2>∠3 B.∠1+∠2=∠3
C.∠1+∠2<∠3 D.∠1+∠2与∠3的大小没有关系
二、填空题(每小题3分,共21分)
11.已知∠1与∠2是对顶角,且∠1与∠2又互为补角,那么∠1=__________.
12.如图,如果∠1=40°,∠2=100°,那么∠3的同位角等于__________,∠
3的内错角等于__________,∠3的同旁内角等于__________.
第12题 第13题 第14题
13.如图,直线AB,CD相交于点O,∠AOC=54°,∠1比∠2大10°,则∠1=__________°;∠2=__________°.
14.如图,AB∥CD,∠1=60°,FG平分∠EFD,则∠2=__________°.
15.如图,直线AB,CD相交于点O,OE⊥AB,O为垂足,如果∠EOD=38°,则∠AOC=__________,∠COB=__________.
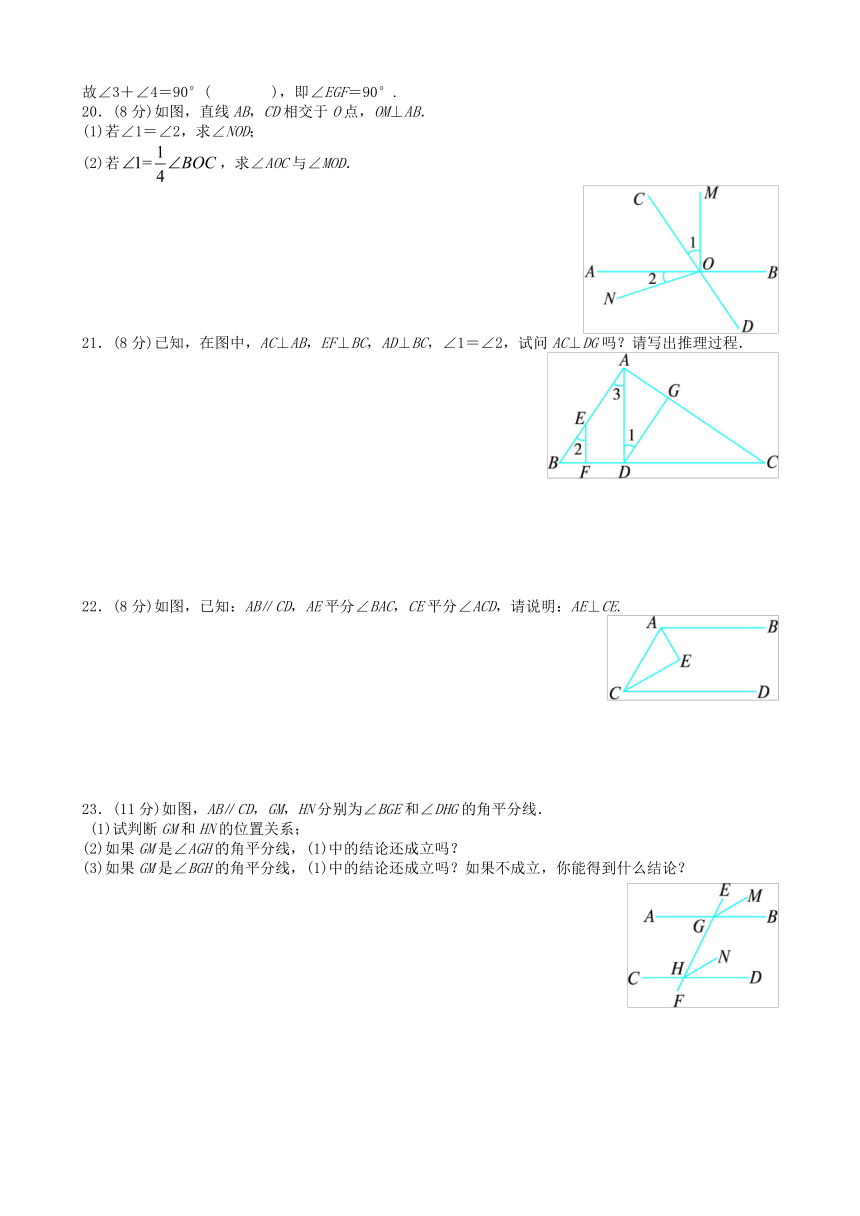
第15题 第16题 第17题
16.如图,线段CD是线段AB经过向右平移__________格,并向下平移__________格得到的线段.
17.如图,是我们生活中经常接触的小刀,刀片的外形是一个直角梯形,刀片上、下是平行的,转动刀片时会形成∠1和∠2,则∠1+∠2=__________度.
三、解答题(本大题共6小题,满分49分.解答需写出解题步骤)
18.(6分)将如图所示的三角形ABC先水平向右平移5格,再竖直向下平移4格得到三角形DEF.
19.(8分)完成下面的推理:已知,如图,AB∥CD∥GH,EG平分∠BEF,FG平分∠EFD,试说明:∠EGF=90°.
因为HG∥AB(已知),
所以∠1=∠3( ).
又因为HG∥CD(已知),
所以∠2=∠4( ).
因为AB∥CD(已知),
所以∠BEF+__________=180°( ).
又因为EG平分∠BEF(已知),
所以∠__________( ).
又因为FG平分∠EFD(已知),
所以∠__________( ).
因此(__________+__________),
即∠1+∠2=90°,
故∠3+∠4=90°( ),即∠EGF=90°.
20.(8分)如图,直线AB,CD相交于O点,OM⊥AB.
(1)若∠1=∠2,求∠NOD;
(2)若,求∠AOC与∠MOD.
21.(8分)已知,在图中,AC⊥AB,EF⊥BC,AD⊥BC,∠1=∠2,试问AC⊥DG吗?请写出推理过程.
22.(8分)如图,已知:AB∥CD,AE平分∠BAC,CE平分∠ACD,请说明:AE⊥CE.
23.(11分)如图,AB∥CD,GM,HN分别为∠BGE和∠DHG的角平分线.
(1)试判断GM和HN的位置关系;
(2)如果GM是∠AGH的角平分线,(1)中的结论还成立吗?
(3)如果GM是∠BGH的角平分线,(1)中的结论还成立吗?如果不成立,你能得到什么结论?
参考答案
1.D 2.A 3.B 4.D 5.D 6.C 7.C 8.B 9.D 10.B
11. 90° 12. 80° 80° 100° 13. 2 22 14. 30 15. 52° 128° 16. 2 2 17. 90
18.解:根据平移作图的方法作图即可.把△ABC的各顶点向右平移5格,再向下平移4格,顺次连接各顶点即为△DEF.如图所示.
19.两直线平行,内错角相等 两直线平行,内错角相等 ∠EFD 两直线平行,同旁内角互补 BEF 角平分线定义 EFD 角平分线定义 ∠BEF ∠EFD 等式性质
20.解:(1)因∠AOD与∠COB为对顶角,且∠1=∠2,则∠MOB=∠NOD,又因OM⊥AB,则∠NOD=∠MOB=90°.
(2)因∠MOB=90°,∠1=∠BOC,则知∠1=30°.而∠AOC+∠1=90°,所以∠AOC=60°.
而∠1+∠MOD=180°,则∠MOD=150°.
21.解:AC⊥DG.理由如下:
∵EF⊥BC,AD⊥BC,∴EF∥AD(垂直于同一直线的两直线平行).故∠2=∠3(两直线平行,同位角相等).
又∵∠1=∠2,∴∠3=∠1(等量代换).于是DG∥AB(内错角相等,两直线平行).
从而可知∠BAC=∠DGC(两直线平行,同位角相等).
∵AB⊥AC,∴∠BAC=90°(垂直的定义).因此∠DGC=90°(等量代换),故AC⊥DG(垂直的定义).
22.证明:如图所示,过E点作EF∥AB,
因为AB∥CD(已知),所以EF∥AB∥CD(平行于同一条直线的两直线平行).
故∠1=∠2,∠4=∠3.(两直线平行内错角相等).因为AE平分∠BAC,CE平分∠ACD,
所以∠1=∠BAC,∠3=∠DCA.
因为∠BAC+∠DCA=180°,所以∠4+∠2=∠1+∠3=(∠BAC+∠DCA)=×180°=90°,
即∠AEC=90°.故AE⊥CE.
23.解:(1)GM∥HN.理由:由AB∥CD,可得∠BGE=∠DHG.因为∠MGE=∠BGE,∠NHG=∠DHG,所以∠MGE=∠NHG.故GM∥HN.
(2)如图,(1)中的结论仍然成立.
理由:因为AB∥CD,所以∠AGH=∠DHG.又因为∠MGH=∠AGH,∠NHG=∠DHG,所以∠MGH=∠NHG.
因此GM∥HN.
(3)如图,(1)中的结论不成立.
结论:GM⊥HN.
理由:因为AB∥CD,
所以∠BGH+∠DHG=180°.
又因为∠HGM=∠BGH,∠GHN=∠DHG,
所以∠HGM+∠GHN=90°.
故∠GKH=90°,即GM⊥HN.
(时间:90分钟 满分:100分)
一、选择题(每小题3分,共30分)
1.下列说法中正确的是( ).
A.有且只有一条直线垂直于已知直线
B.互相垂直的两条线段一定相交
C.从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离
D.直线c外一点A与直线c上各点连接而成的所有线段中,最短的线段长是3 cm,则点A到直线c的距离是3 cm
2.在下图右侧的四个三角形中,能由△ABC经过平移得到的是( ).
3.如图,下列说法错误的是( ).
A.∠A与∠C是同旁内角 B.∠1与∠3是同位角
C.∠2与∠3是内错角 D.∠3与∠B是同旁内角
第3题 第4题 第5题
4.如图,直线AB,CD相交于点O,OE⊥CD于点O,∠AOC=36°,则∠BOE=( ).
A.36° B.64° C.144° D.54°
5.如图,直线a,b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°.其中能判断a∥b的条件是( ).
A.①③ B.②④ C.①③④ D.①②③④
6.已知OA⊥OC,∠AOB∶∠AOC=2∶3,则∠BOC的度数为( ).
A.30° B.150° C.30°或150° D.不同于以上答案
7.如图,AB∥CD,∠DCE=80°,则∠BEF=( ).
A.120° B.110° C.100° D.80°
第7题 第8题 第9题 第10题
8.如图,AB⊥BC,BC⊥CD,∠EBC=∠BCF,那么∠ABE与∠DCF的位置和大小关系是( ).
A.是同位角且相等 B.不是同位角但相等
C.是同位角但不等 D.不是同位角也不等
9.如图,一条公路修到湖边时,需拐弯绕湖而过,如果第一次拐的角∠A是120°,第二次拐的角∠B是150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C是( ).
A.120° B.130° C.140° D.150°
10.如图,已知AB∥CD,AD∥BC,∠ABE是平角,则下列说法中正确的是( ).
A.∠1=∠2>∠3 B.∠1+∠2=∠3
C.∠1+∠2<∠3 D.∠1+∠2与∠3的大小没有关系
二、填空题(每小题3分,共21分)
11.已知∠1与∠2是对顶角,且∠1与∠2又互为补角,那么∠1=__________.
12.如图,如果∠1=40°,∠2=100°,那么∠3的同位角等于__________,∠
3的内错角等于__________,∠3的同旁内角等于__________.
第12题 第13题 第14题
13.如图,直线AB,CD相交于点O,∠AOC=54°,∠1比∠2大10°,则∠1=__________°;∠2=__________°.
14.如图,AB∥CD,∠1=60°,FG平分∠EFD,则∠2=__________°.
15.如图,直线AB,CD相交于点O,OE⊥AB,O为垂足,如果∠EOD=38°,则∠AOC=__________,∠COB=__________.
第15题 第16题 第17题
16.如图,线段CD是线段AB经过向右平移__________格,并向下平移__________格得到的线段.
17.如图,是我们生活中经常接触的小刀,刀片的外形是一个直角梯形,刀片上、下是平行的,转动刀片时会形成∠1和∠2,则∠1+∠2=__________度.
三、解答题(本大题共6小题,满分49分.解答需写出解题步骤)
18.(6分)将如图所示的三角形ABC先水平向右平移5格,再竖直向下平移4格得到三角形DEF.
19.(8分)完成下面的推理:已知,如图,AB∥CD∥GH,EG平分∠BEF,FG平分∠EFD,试说明:∠EGF=90°.
因为HG∥AB(已知),
所以∠1=∠3( ).
又因为HG∥CD(已知),
所以∠2=∠4( ).
因为AB∥CD(已知),
所以∠BEF+__________=180°( ).
又因为EG平分∠BEF(已知),
所以∠__________( ).
又因为FG平分∠EFD(已知),
所以∠__________( ).
因此(__________+__________),
即∠1+∠2=90°,
故∠3+∠4=90°( ),即∠EGF=90°.
20.(8分)如图,直线AB,CD相交于O点,OM⊥AB.
(1)若∠1=∠2,求∠NOD;
(2)若,求∠AOC与∠MOD.
21.(8分)已知,在图中,AC⊥AB,EF⊥BC,AD⊥BC,∠1=∠2,试问AC⊥DG吗?请写出推理过程.
22.(8分)如图,已知:AB∥CD,AE平分∠BAC,CE平分∠ACD,请说明:AE⊥CE.
23.(11分)如图,AB∥CD,GM,HN分别为∠BGE和∠DHG的角平分线.
(1)试判断GM和HN的位置关系;
(2)如果GM是∠AGH的角平分线,(1)中的结论还成立吗?
(3)如果GM是∠BGH的角平分线,(1)中的结论还成立吗?如果不成立,你能得到什么结论?
参考答案
1.D 2.A 3.B 4.D 5.D 6.C 7.C 8.B 9.D 10.B
11. 90° 12. 80° 80° 100° 13. 2 22 14. 30 15. 52° 128° 16. 2 2 17. 90
18.解:根据平移作图的方法作图即可.把△ABC的各顶点向右平移5格,再向下平移4格,顺次连接各顶点即为△DEF.如图所示.
19.两直线平行,内错角相等 两直线平行,内错角相等 ∠EFD 两直线平行,同旁内角互补 BEF 角平分线定义 EFD 角平分线定义 ∠BEF ∠EFD 等式性质
20.解:(1)因∠AOD与∠COB为对顶角,且∠1=∠2,则∠MOB=∠NOD,又因OM⊥AB,则∠NOD=∠MOB=90°.
(2)因∠MOB=90°,∠1=∠BOC,则知∠1=30°.而∠AOC+∠1=90°,所以∠AOC=60°.
而∠1+∠MOD=180°,则∠MOD=150°.
21.解:AC⊥DG.理由如下:
∵EF⊥BC,AD⊥BC,∴EF∥AD(垂直于同一直线的两直线平行).故∠2=∠3(两直线平行,同位角相等).
又∵∠1=∠2,∴∠3=∠1(等量代换).于是DG∥AB(内错角相等,两直线平行).
从而可知∠BAC=∠DGC(两直线平行,同位角相等).
∵AB⊥AC,∴∠BAC=90°(垂直的定义).因此∠DGC=90°(等量代换),故AC⊥DG(垂直的定义).
22.证明:如图所示,过E点作EF∥AB,
因为AB∥CD(已知),所以EF∥AB∥CD(平行于同一条直线的两直线平行).
故∠1=∠2,∠4=∠3.(两直线平行内错角相等).因为AE平分∠BAC,CE平分∠ACD,
所以∠1=∠BAC,∠3=∠DCA.
因为∠BAC+∠DCA=180°,所以∠4+∠2=∠1+∠3=(∠BAC+∠DCA)=×180°=90°,
即∠AEC=90°.故AE⊥CE.
23.解:(1)GM∥HN.理由:由AB∥CD,可得∠BGE=∠DHG.因为∠MGE=∠BGE,∠NHG=∠DHG,所以∠MGE=∠NHG.故GM∥HN.
(2)如图,(1)中的结论仍然成立.
理由:因为AB∥CD,所以∠AGH=∠DHG.又因为∠MGH=∠AGH,∠NHG=∠DHG,所以∠MGH=∠NHG.
因此GM∥HN.
(3)如图,(1)中的结论不成立.
结论:GM⊥HN.
理由:因为AB∥CD,
所以∠BGH+∠DHG=180°.
又因为∠HGM=∠BGH,∠GHN=∠DHG,
所以∠HGM+∠GHN=90°.
故∠GKH=90°,即GM⊥HN.
