16.2分式的混合运算是专题训练( 附答案及解析)
文档属性
| 名称 | 16.2分式的混合运算是专题训练( 附答案及解析) |  | |
| 格式 | zip | ||
| 文件大小 | 228.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-22 18:59:16 | ||
图片预览

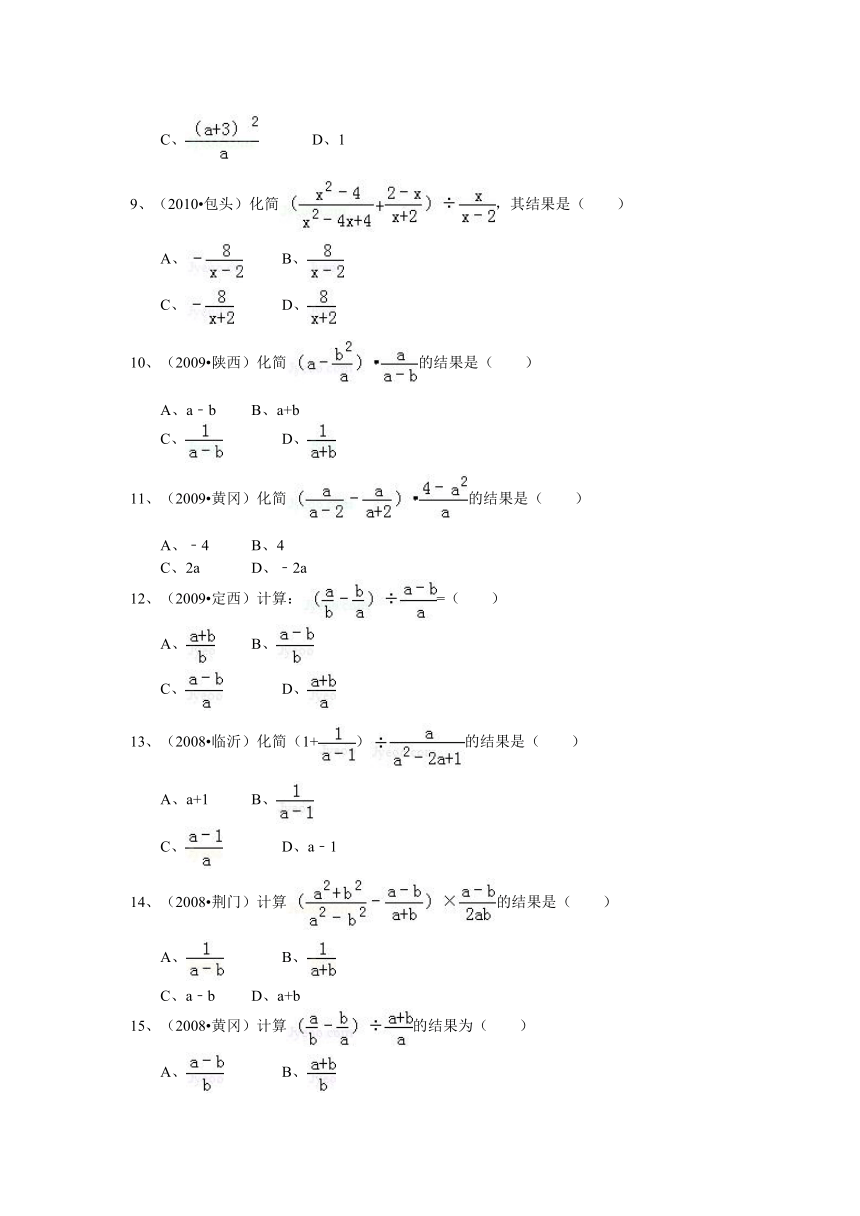


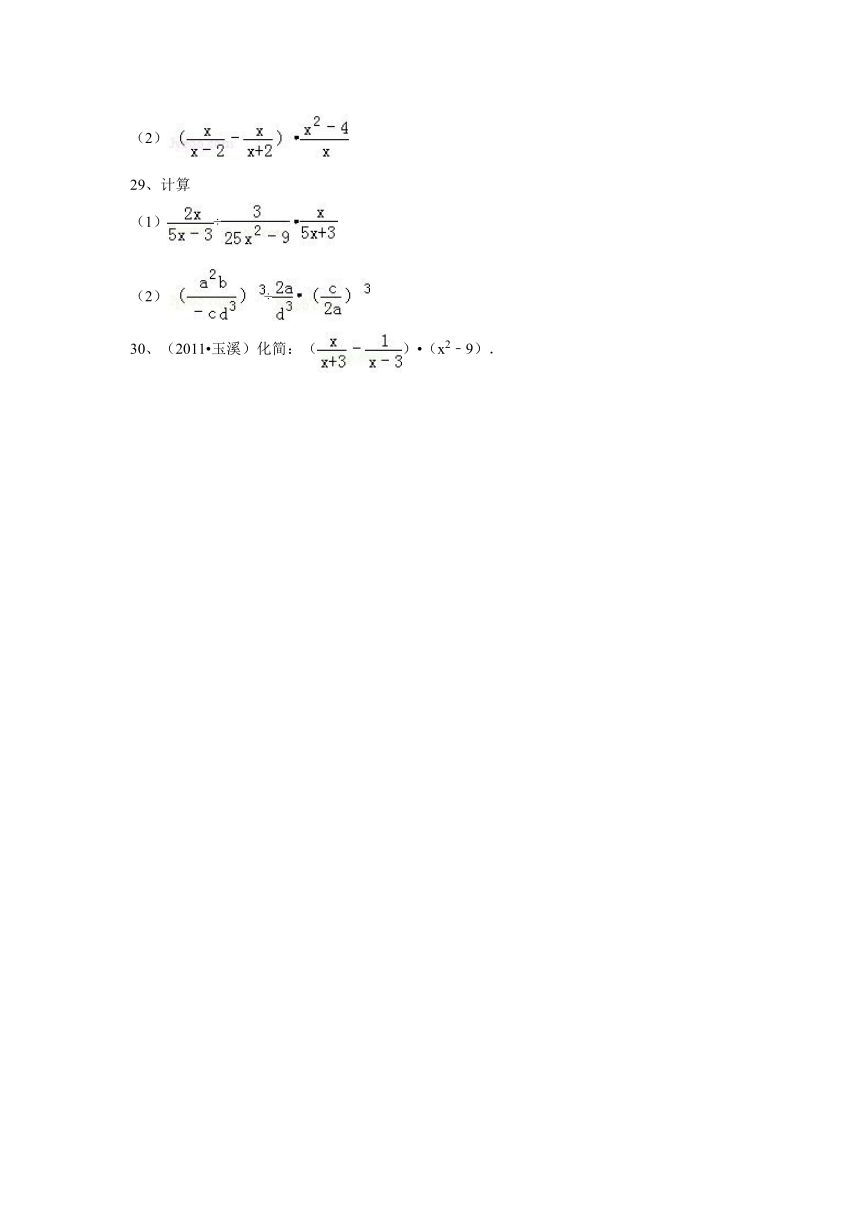
文档简介
分式的混合运算 专题训练
一、选择题(共20小题)
1、(2011 孝感)化简的结果是( )
A、 B、
C、 D、y
2、(2011 威海)计算1÷的结果是( )
A、﹣m2﹣2m﹣1 B、﹣m2+2m﹣1
C、m2﹣2m﹣1 D、m2﹣1
3、(2011 宁德)已知:a1=x+1(x≠0且x≠﹣1),a2=1÷(1﹣a1),a3=1÷(1﹣a2),…,an=1÷(1﹣an﹣1),则a2011等于( )
A、x B、x+1
C、 D、
4、(2011 牡丹江)下列计算正确的是( )
A、2a3+a2=2a5 B、(﹣2ab)3=﹣2ab3
C、2a3÷a2=2a D、
5、(2011 临沂)化简(x﹣)÷(1﹣)的结果是( )
A、 B、x﹣1
C、 D、
6、(2011 江汉区)化简的结果是( )
A、0 B、1
C、﹣1 D、(m+2)2
7、(2010 随州)化简:的结果是( )
A、2 B、
C、 D、
8、(2010 河池)化简:的结果是( )
A、﹣a B、a
C、 D、1
9、(2010 包头)化简,其结果是( )
A、 B、
C、 D、
10、(2009 陕西)化简的结果是( )
A、a﹣b B、a+b
C、 D、
11、(2009 黄冈)化简的结果是( )
A、﹣4 B、4
C、2a D、﹣2a
12、(2009 定西)计算:=( )
A、 B、
C、 D、
13、(2008 临沂)化简(1+)的结果是( )
A、a+1 B、
C、 D、a﹣1
14、(2008 荆门)计算的结果是( )
A、 B、
C、a﹣b D、a+b
15、(2008 黄冈)计算的结果为( )
A、 B、
C、 D、
16、(2007 威海)下列各式计算正确的是( )
A、 B、
C、 D、
17、(2007 济南)计算的结果为( )
A、 B、
C、 D、
18、(2006 武汉)计算(﹣a)÷(1﹣)的正确结果是( )
A、a﹣1 B、﹣a﹣1
C、1﹣a D、a+1
19、(2006 温州)晓晓根据下表,作了三个推测:
x 1 10 100 1000 10000 …
3﹣ 3 2.1 2.01 2.001 2.0001 …
①3﹣(x>0)的值随着x的增大越来越小;
②3﹣(x>0)的值有可能等于2;
③3﹣(x>0)的值随着x的增大越来越接近于2.
则推测正确的有( )
A、0个 B、1个
C、2个 D、3个
20、(2006 黄冈)计算:的结果为( )
A、1 B、
C、 D、
二、填空题(共2小题)
21、(2011 泰安)化简:的结果为 _________ .
22、(2011 昆明)计算:= _________ .
三、解答题(共8小题)
23、计算或化简:
(1)
(2)
(3)
(4).
24、计算:
(1)(﹣3a2b)2 (8a2b2);
(2)(x+2)2﹣(x+1)(x﹣1);
(3).
25、计算或化简:
(1)﹣4x3y[7x2y﹣3x2y3+(2x2y)3];
(2)(2x﹣3y)2﹣(x﹣2y)(x+2y);
(3)(x2x3)2÷(x3)2;
(4)1﹣.
26、计算或化简:
(1)﹣2x2y[(﹣2xy2)3+1];
(2)(2a+b)2﹣(a+2b)(a﹣2b);
(3)(﹣y3 y)2÷(﹣y)2;
(4)﹣x+y.
27、化简下列各式:
(1)z
(2)
(3)[(2x+y)2﹣y(y+4x)﹣8x]÷2x
(4).
28、化简:
(1)
(2)
29、计算
(1)÷
(2)÷
30、(2011 玉溪)化简:() (x2﹣9).
答案与评分标准
一、选择题(共20小题)
1、(2011 孝感)化简的结果是( )
A、 B、
C、 D、y
考点:分式的混合运算。
分析:首先利用分式的加减运算法则计算括号里面的,然后再利用分式的乘除运算法则求得结果.
解答:解:= = =.
故选B.
点评:此题考查了分式的混合运算,通分、因式分解和约分是解答的关键.解题时还要注意运算顺序.
2、(2011 威海)计算1÷的结果是( )
A、﹣m2﹣2m﹣1 B、﹣m2+2m﹣1
C、m2﹣2m﹣1 D、m2﹣1
考点:分式的混合运算。
专题:计算题。
分析:首先将除法变为乘法运算,即乘以除数的倒数,然后利用乘法运算法则约分求解即可求得答案.
解答:解:1÷=1××(m+1)(m﹣1)=﹣(m﹣1)2=﹣m2+2m﹣1.
故选B.
点评:此题考查了分式的乘除混合运算.解题的关键是注意运算顺序:同级运算,从左到右依次进行.
3、(2011 宁德)已知:a1=x+1(x≠0且x≠﹣1),a2=1÷(1﹣a1),a3=1÷(1﹣a2),…,an=1÷(1﹣an﹣1),则a2011等于( )
A、x B、x+1
C、 D、
考点:分式的混合运算。
专题:规律型。
分析:先计算出a2=﹣,a3=,a4=x+1,…,依次循环,每三个数为一轮,则a3n=,a3n+1=x+1,a3n+1=﹣,从而得出a2011即可.
解答:解:∵a1=x+1(x≠0且x≠﹣1),a2=1÷(1﹣a1),a3=1÷(1﹣a2),…,an=1÷(1﹣an﹣1),
∴a2=﹣,a3=,a4=x+1,…,
∴a3n=,a3n+1=x+1,a3n+2=﹣,
∵2011=670×3+1,
∴a2011=x+1.
故选B.
点评:本题是一道找规律的题目,考查了分式的混合运算,解题的关键是得出规律:a3n=,a3n+1=x+1,a3n+1=﹣.
4、(2011 牡丹江)下列计算正确的是( )
A、2a3+a2=2a5 B、(﹣2ab)3=﹣2ab3
C、2a3÷a2=2a D、
考点:分式的混合运算;合并同类项;幂的乘方与积的乘方;同底数幂的除法。
专题:计算题。
分析:根据合并同类项、幂的乘方与积的乘方、同底数幂的除法以及分式的混合运算法则依次计算即可.
解答:解:A、2a3+a2≠2a5,不是同类项不能合并,故本选项错误;
B、(﹣2ab)3=﹣8a3b3,故本选项错误;
C、2a3÷a2=2a,故本选项正确;
D、a÷b =,故本选项错误.
故选C.
点评:本题考查了合并同类项、幂的乘方与积的乘方、同底数幂的除法以及分式的混合运算法则,牢记法则是关键.
5、(2011 临沂)化简(x﹣)÷(1﹣)的结果是( )
A、 B、x﹣1
C、 D、
考点:分式的混合运算。
分析:首先利用分式的加法法则,求得括号里面的值,再利用除法法则求解即可求得答案.
解答:解:(x﹣)÷(1﹣),
=÷,
= ,
=x﹣1.
故选B.
点评:此题考查了分式的混合运算.解题时要注意运算顺序.
6、(2011 江汉区)化简的结果是( )
A、0 B、1
C、﹣1 D、(m+2)2
考点:分式的混合运算。
专题:计算题。
分析:本题要先通分,分母变为m﹣2后,分子为m2﹣4,然后约分,便可得出答案.
解答:解:原式=÷(m+2),
=,
=1.
故选B.
点评:本题主要考查分式的混合运算,通分、因式分解和约分是解答的关键,属于基础题.
7、(2010 随州)化简:的结果是( )
A、2 B、
C、 D、
考点:分式的混合运算。
分析:先把括号中的第二个分式约分,再利用乘法分配律把(x﹣3)分别与括号中的式子相乘可使计算简便.
解答:解:
=(﹣) (x﹣3)
= (x﹣3)﹣ (x﹣3)
=1﹣
=.
故选B.
点评:归纳提炼:对于一般的分式混合运算来讲,其运算顺序与整式混合运算一样,是先乘方,再乘除,最后算加减,如果遇括号要先算括号里面的.在此基础上,有时也应该根据具体问题的特点,灵活应变,注意方法.
8、(2010 河池)化简:的结果是( )
A、﹣a B、a
C、 D、1
考点:分式的混合运算。
分析:先计算括号里的,再把除法转化成乘法计算.
解答:解:==a.
故选B.
点评:对于一般的分式混合运算来讲,其运算顺序与整式混合运算一样,是先乘方,再乘除,最后算加减,如果遇括号要先算括号里面的.
9、(2010 包头)化简,其结果是( )
A、 B、
C、 D、
考点:分式的混合运算。
分析:对于分式混合运算,其实也就是在同一个算式中,综合了分式的加减、乘除及乘方中的一种或几种运算,关键是要注意各种运算的先后顺序.
解答:解:原式=[+]×
=+)×,
=﹣,
=,
=,
=,
故选D.
点评:对于一般的分式混合运算来讲,其运算顺序与整式混合运算一样,是先乘方,再乘除,最后算加减,如果遇括号要先算括号里面的.在此基础上,有时也应该根据具体问题的特点,灵活应变,注意方法.
10、(2009 陕西)化简的结果是( )
A、a﹣b B、a+b
C、 D、
考点:分式的混合运算。
专题:计算题。
分析:先算括号里式子,再进行因式分解,最后进行分式的约分化简.
解答:解:==a+b,故选B.
点评:本题考查分式的运算,运算顺序是:先括号里,经过通分,再做乘法,约分化为最简.
11、(2009 黄冈)化简的结果是( )
A、﹣4 B、4
C、2a D、﹣2a
考点:分式的混合运算。
专题:计算题。
分析:由(a+b)c=ab+bc,运用分配律可约去各个分式的分母,使计算简便.
解答:解:原式=﹣(a+2)+(a﹣2)=﹣4,故选A.
点评:此题根据乘法的分配律先进行分式的乘法运算,然后再进行加减的运算,使运算简单化了,计算过程要注意符号间的变化.
12、(2009 定西)计算:=( )
A、 B、
C、 D、
考点:分式的混合运算。
专题:计算题。
分析:先算括号里式子,再把除法转化为乘法运算,最后进行分式的约分化简.
解答:解:==,故选A.
点评:注意此题的运算顺序:先括号里,经过通分,再把除法转化为乘法,约分化为最简.
13、(2008 临沂)化简(1+)的结果是( )
A、a+1 B、
C、 D、a﹣1
考点:分式的混合运算。
专题:计算题。
分析:先算括号里式子,再进行因式分解,最后把除法转化为乘法运算,进行分式的约分化简.
解答:解:(1+)==a﹣1.
故选D.
点评:当整式与分式相加减时,一般可以把整式看作分母为1的分式,与其它分式进行通分运算.
14、(2008 荆门)计算的结果是( )
A、 B、
C、a﹣b D、a+b
考点:分式的混合运算。
专题:计算题。
分析:先算小括号里的,再算乘法,约分化简即可.
解答:解:==,故选B.
点评:考查分式的化简,分式的化简关键在于通过通分、合并同类项、因式分解、约分转化为最简分式.
15、(2008 黄冈)计算的结果为( )
A、 B、
C、 D、
考点:分式的混合运算。
专题:计算题。
分析:先算小括号里的,再把除法统一成乘法,约分化为最简.
解答:解:==,故选A.
点评:分式的四则运算是整式四则运算的进一步发展,在计算时,首先要弄清楚运算顺序,先去括号,再进行分式的乘除.
16、(2007 威海)下列各式计算正确的是( )
A、 B、
C、 D、
考点:分式的混合运算;约分。
分析:按同底数幂除法法则,约分,分式混合运算法则进行运算,看结果是否正确即可.
解答:解:A、式应该为x3,错误;
B、分解正确;
C、的结果应该为﹣m﹣3,错误;
D、=,错误.
故选B.
点评:本题主要考查分式的混合运算,不是很难.
17、(2007 济南)计算的结果为( )
A、 B、
C、 D、
考点:分式的混合运算。
分析:先计算括号里的,再相乘.
解答:解:
=
=﹣
=﹣.
故选A.
点评:本题的关键是通分、分解因式、约分,用到了平方差公式.
18、(2006 武汉)计算(﹣a)÷(1﹣)的正确结果是( )
A、a﹣1 B、﹣a﹣1
C、1﹣a D、a+1
考点:分式的混合运算。
专题:计算题。
分析:先算括号里的通分,再进行因式分解,把除号换为乘号,最后再进行分式间的约分化简.
解答:解:原式==﹣a﹣1,故选B.
点评:注意混合运算时要先算括号里的,再算乘除.
19、(2006 温州)晓晓根据下表,作了三个推测:
x 1 10 100 1000 10000 …
3﹣ 3 2.1 2.01 2.001 2.0001 …
①3﹣(x>0)的值随着x的增大越来越小;
②3﹣(x>0)的值有可能等于2;
③3﹣(x>0)的值随着x的增大越来越接近于2.
则推测正确的有( )
A、0个 B、1个
C、2个 D、3个
考点:分式的混合运算。
专题:图表型。
分析:考查分式化简及混合运算.
解答:解:①观察式子3﹣,
可以看到分式可以化简为=﹣=1﹣,
所以,3﹣=3﹣(1﹣)=3﹣1+=2+.
当x>0时,会随着x的增大而减小.
所以,2+会随着x的增大而减小,故①对;
②分母不能为0,故的值不可能等于2,故②不对;
③又因为当x>0时,>0,所以2+>2,且会随着x的增大而越来越接近2,故正确.
故选C.
点评:此题考查分式的性质,注意分式的化简及因变量的取值与自变量的取值之间的联系.
20、(2006 黄冈)计算:的结果为( )
A、1 B、
C、 D、
考点:分式的混合运算。
专题:计算题。
分析:把第二个分式的分母先因式分解,再把除法统一成乘法,再算减法,化简即可.
解答:解:===1,故选A.
点评:此题要注意运算顺序,先乘除后加减,还要注意9﹣m2变形为﹣(m2﹣9).
二、填空题(共2小题)
21、(2011 泰安)化简:的结果为 x﹣6 .
考点:分式的混合运算。
专题:计算题。
分析:先将括号里面的通分合并同类项,然后将除法转换成乘法,约分化简得到最简代数式.
解答:解:原式=×
=×
=x﹣6
故答案为:x﹣6
点评:本题主要考查分式的混合运算,通分、因式分解和约分是解答的关键.
22、(2011 昆明)计算:= a .
考点:分式的混合运算。
分析:首先对括号内的式子通分相减,然后把除法转化为乘法,约分计算即可.
解答:解:原式=(+)
=
===a.
故答案是:a
点评:本题主要考查分式的混合运算,通分、因式分解和约分是解答的关键.
三、解答题(共8小题)
23、计算或化简:
(1)
(2)
(3)
(4).
考点:实数的运算;分式的混合运算。
分析:(1)根据绝对值的意义去掉绝对值的符号即可进行计算;
(2)根据负整数指数幂的规定和实数的计算法则进行计算;
(3)利用分式的计算法则进行计算;
(4)利用分式的计算法则和幂的定义进行计算.
解答:解:(1)原式=+2﹣+2=4﹣;
(2)原式=1﹣8﹣3+9=﹣1;
(3)原式===a+2;
(4)原式==.
点评:此题分别考查了绝对值的定义,实数的计算,幂的定义,分式的计算等知识,计算时一定要注意符号的处理.
24、计算:
(1)(﹣3a2b)2 (8a2b2);
(2)(x+2)2﹣(x+1)(x﹣1);
(3).
考点:整式的混合运算;分式的混合运算。
分析:(1)(2)考查了整式的混合运算;
(3)考查了分式的混合运算,整式与分式的混合运算的顺序都是先括号,再乘除.
解答:解:(1)原式=9a4b2 (8a2b2)=72a6b4;
(2)原式=x2+4x+4﹣x2+1=4x+5;
(3)原式=(﹣) = =.
点评:对于一般的分式混合运算来讲,其运算顺序与整式混合运算一样,是先乘方,再乘除,最后算加减,如果遇括号要先算括号里面的.在此基础上,有时也应该根据具体问题的特点,灵活应变,注意方法.
25、计算或化简:
(1)﹣4x3y[7x2y﹣3x2y3+(2x2y)3];
(2)(2x﹣3y)2﹣(x﹣2y)(x+2y);
(3)(x2x3)2÷(x3)2;
(4)1﹣.
考点:整式的混合运算;分式的混合运算。
专题:计算题。
分析:(1)主要考查了单项式与多项式的乘法;
(2)运用完全平方公式和平方差公式即可;
(3)底数不变,指数按运算法则计算即可;
(4)先通分再加减.
解答:解:(1)原式=﹣28x5y2+12x5y4﹣32x9y4;
(2)原式=4y2﹣12xy+9y2﹣x2+4y=23x2﹣12xy+13y2;
(3)原式=x10÷x6=x4;
(4)原式=1﹣×[×]=1﹣×=.
点评:此题主要考查了有理数的混合运算:首先要弄清楚运算顺序,先去括号,再进行有理数的乘除,最后是加减.
26、计算或化简:
(1)﹣2x2y[(﹣2xy2)3+1];
(2)(2a+b)2﹣(a+2b)(a﹣2b);
(3)(﹣y3 y)2÷(﹣y)2;
(4)﹣x+y.
考点:整式的混合运算;分式的混合运算。
专题:计算题。
分析:根据整式的运算法则和分式的运算法则进行计算.
解答:解:(1)原式=16x5y7﹣2x2y;
(2)原式=4a2+4ab+b2﹣a2+4b=3a2+4ab+5b2;
(3)原式=y6;
(4)原式==.
点评:本题主要考查分式和整式的运算,注意运算顺序.
27、化简下列各式:
(1)z
(2)
(3)[(2x+y)2﹣y(y+4x)﹣8x]÷2x
(4).
考点:整式的混合运算;分式的混合运算。
专题:计算题。
分析:有理数的混合运算首先要弄清楚运算顺序,先去括号,再进行有理数的乘除,最后是加减.
解答:解:
(1)原式=x3y3z;
(2)原式=2a3b2﹣a2b3;
(3)原式=(4x2+4xy+y2﹣y2﹣4xy﹣8x)÷2x=2x﹣4;
(4)原式=×=2x﹣4.
故答案为x3y3z.
点评:规律总结:对于一般的分式混合运算来讲,其运算顺序与整式混合运算一样,是先乘方,再乘除,最后算加减,如果遇括号要先算括号里面的.在此基础上,有时也应该根据具体问题的特点,灵活应变,注意方法.
28、化简:
(1)
(2)
考点:分式的乘除法;分式的混合运算。
专题:计算题。
分析:(1)是分式的加法运算,先化为同分母分式,然后根据分式的加减法法则进行运算.
(2)是分式加减乘除混合运算,计算时应先算乘除,后算加减,有括号,先算括号里面的.
解答:解:(1)原式===;
(2)原式===4.
点评:对于分式运算,若是加减运算,先把异分母化为同分母,再进行计算.若是加减乘除混合运算,应注意先因式分解,再约分,并且各种运算的结果必须是最简分式.
29、计算
(1)÷
(2)÷
考点:分式的乘除法;分式的混合运算。
专题:计算题。
分析:(1)首先把除法运算转化成乘法运算,然后因式分解因式进行约分.(2)乘方的运用,注意符号.
解答:解:(1)原式=
=2x x
=
(2)原式=
=﹣.
点评:在分式的乘除运算中,除了准确运用分式的运算法则外,还要灵活运用因式分解和乘方法则.
30、(2011 玉溪)化简:() (x2﹣9).
考点:分式的混合运算。
分析:先把(x2﹣9)分解为(x+3)(x﹣3),再利用乘法的分配律分别与括号里的各项相乘,最后去括号合并同类项即可.
解答:解:() (x2﹣9)
=
=x(x﹣3)﹣(x+3)
=x2﹣3x﹣x﹣3
=x2﹣4x﹣3.
点评:此题考查了分式的混合运算,解题时要注意简便方法的应用.
一、选择题(共20小题)
1、(2011 孝感)化简的结果是( )
A、 B、
C、 D、y
2、(2011 威海)计算1÷的结果是( )
A、﹣m2﹣2m﹣1 B、﹣m2+2m﹣1
C、m2﹣2m﹣1 D、m2﹣1
3、(2011 宁德)已知:a1=x+1(x≠0且x≠﹣1),a2=1÷(1﹣a1),a3=1÷(1﹣a2),…,an=1÷(1﹣an﹣1),则a2011等于( )
A、x B、x+1
C、 D、
4、(2011 牡丹江)下列计算正确的是( )
A、2a3+a2=2a5 B、(﹣2ab)3=﹣2ab3
C、2a3÷a2=2a D、
5、(2011 临沂)化简(x﹣)÷(1﹣)的结果是( )
A、 B、x﹣1
C、 D、
6、(2011 江汉区)化简的结果是( )
A、0 B、1
C、﹣1 D、(m+2)2
7、(2010 随州)化简:的结果是( )
A、2 B、
C、 D、
8、(2010 河池)化简:的结果是( )
A、﹣a B、a
C、 D、1
9、(2010 包头)化简,其结果是( )
A、 B、
C、 D、
10、(2009 陕西)化简的结果是( )
A、a﹣b B、a+b
C、 D、
11、(2009 黄冈)化简的结果是( )
A、﹣4 B、4
C、2a D、﹣2a
12、(2009 定西)计算:=( )
A、 B、
C、 D、
13、(2008 临沂)化简(1+)的结果是( )
A、a+1 B、
C、 D、a﹣1
14、(2008 荆门)计算的结果是( )
A、 B、
C、a﹣b D、a+b
15、(2008 黄冈)计算的结果为( )
A、 B、
C、 D、
16、(2007 威海)下列各式计算正确的是( )
A、 B、
C、 D、
17、(2007 济南)计算的结果为( )
A、 B、
C、 D、
18、(2006 武汉)计算(﹣a)÷(1﹣)的正确结果是( )
A、a﹣1 B、﹣a﹣1
C、1﹣a D、a+1
19、(2006 温州)晓晓根据下表,作了三个推测:
x 1 10 100 1000 10000 …
3﹣ 3 2.1 2.01 2.001 2.0001 …
①3﹣(x>0)的值随着x的增大越来越小;
②3﹣(x>0)的值有可能等于2;
③3﹣(x>0)的值随着x的增大越来越接近于2.
则推测正确的有( )
A、0个 B、1个
C、2个 D、3个
20、(2006 黄冈)计算:的结果为( )
A、1 B、
C、 D、
二、填空题(共2小题)
21、(2011 泰安)化简:的结果为 _________ .
22、(2011 昆明)计算:= _________ .
三、解答题(共8小题)
23、计算或化简:
(1)
(2)
(3)
(4).
24、计算:
(1)(﹣3a2b)2 (8a2b2);
(2)(x+2)2﹣(x+1)(x﹣1);
(3).
25、计算或化简:
(1)﹣4x3y[7x2y﹣3x2y3+(2x2y)3];
(2)(2x﹣3y)2﹣(x﹣2y)(x+2y);
(3)(x2x3)2÷(x3)2;
(4)1﹣.
26、计算或化简:
(1)﹣2x2y[(﹣2xy2)3+1];
(2)(2a+b)2﹣(a+2b)(a﹣2b);
(3)(﹣y3 y)2÷(﹣y)2;
(4)﹣x+y.
27、化简下列各式:
(1)z
(2)
(3)[(2x+y)2﹣y(y+4x)﹣8x]÷2x
(4).
28、化简:
(1)
(2)
29、计算
(1)÷
(2)÷
30、(2011 玉溪)化简:() (x2﹣9).
答案与评分标准
一、选择题(共20小题)
1、(2011 孝感)化简的结果是( )
A、 B、
C、 D、y
考点:分式的混合运算。
分析:首先利用分式的加减运算法则计算括号里面的,然后再利用分式的乘除运算法则求得结果.
解答:解:= = =.
故选B.
点评:此题考查了分式的混合运算,通分、因式分解和约分是解答的关键.解题时还要注意运算顺序.
2、(2011 威海)计算1÷的结果是( )
A、﹣m2﹣2m﹣1 B、﹣m2+2m﹣1
C、m2﹣2m﹣1 D、m2﹣1
考点:分式的混合运算。
专题:计算题。
分析:首先将除法变为乘法运算,即乘以除数的倒数,然后利用乘法运算法则约分求解即可求得答案.
解答:解:1÷=1××(m+1)(m﹣1)=﹣(m﹣1)2=﹣m2+2m﹣1.
故选B.
点评:此题考查了分式的乘除混合运算.解题的关键是注意运算顺序:同级运算,从左到右依次进行.
3、(2011 宁德)已知:a1=x+1(x≠0且x≠﹣1),a2=1÷(1﹣a1),a3=1÷(1﹣a2),…,an=1÷(1﹣an﹣1),则a2011等于( )
A、x B、x+1
C、 D、
考点:分式的混合运算。
专题:规律型。
分析:先计算出a2=﹣,a3=,a4=x+1,…,依次循环,每三个数为一轮,则a3n=,a3n+1=x+1,a3n+1=﹣,从而得出a2011即可.
解答:解:∵a1=x+1(x≠0且x≠﹣1),a2=1÷(1﹣a1),a3=1÷(1﹣a2),…,an=1÷(1﹣an﹣1),
∴a2=﹣,a3=,a4=x+1,…,
∴a3n=,a3n+1=x+1,a3n+2=﹣,
∵2011=670×3+1,
∴a2011=x+1.
故选B.
点评:本题是一道找规律的题目,考查了分式的混合运算,解题的关键是得出规律:a3n=,a3n+1=x+1,a3n+1=﹣.
4、(2011 牡丹江)下列计算正确的是( )
A、2a3+a2=2a5 B、(﹣2ab)3=﹣2ab3
C、2a3÷a2=2a D、
考点:分式的混合运算;合并同类项;幂的乘方与积的乘方;同底数幂的除法。
专题:计算题。
分析:根据合并同类项、幂的乘方与积的乘方、同底数幂的除法以及分式的混合运算法则依次计算即可.
解答:解:A、2a3+a2≠2a5,不是同类项不能合并,故本选项错误;
B、(﹣2ab)3=﹣8a3b3,故本选项错误;
C、2a3÷a2=2a,故本选项正确;
D、a÷b =,故本选项错误.
故选C.
点评:本题考查了合并同类项、幂的乘方与积的乘方、同底数幂的除法以及分式的混合运算法则,牢记法则是关键.
5、(2011 临沂)化简(x﹣)÷(1﹣)的结果是( )
A、 B、x﹣1
C、 D、
考点:分式的混合运算。
分析:首先利用分式的加法法则,求得括号里面的值,再利用除法法则求解即可求得答案.
解答:解:(x﹣)÷(1﹣),
=÷,
= ,
=x﹣1.
故选B.
点评:此题考查了分式的混合运算.解题时要注意运算顺序.
6、(2011 江汉区)化简的结果是( )
A、0 B、1
C、﹣1 D、(m+2)2
考点:分式的混合运算。
专题:计算题。
分析:本题要先通分,分母变为m﹣2后,分子为m2﹣4,然后约分,便可得出答案.
解答:解:原式=÷(m+2),
=,
=1.
故选B.
点评:本题主要考查分式的混合运算,通分、因式分解和约分是解答的关键,属于基础题.
7、(2010 随州)化简:的结果是( )
A、2 B、
C、 D、
考点:分式的混合运算。
分析:先把括号中的第二个分式约分,再利用乘法分配律把(x﹣3)分别与括号中的式子相乘可使计算简便.
解答:解:
=(﹣) (x﹣3)
= (x﹣3)﹣ (x﹣3)
=1﹣
=.
故选B.
点评:归纳提炼:对于一般的分式混合运算来讲,其运算顺序与整式混合运算一样,是先乘方,再乘除,最后算加减,如果遇括号要先算括号里面的.在此基础上,有时也应该根据具体问题的特点,灵活应变,注意方法.
8、(2010 河池)化简:的结果是( )
A、﹣a B、a
C、 D、1
考点:分式的混合运算。
分析:先计算括号里的,再把除法转化成乘法计算.
解答:解:==a.
故选B.
点评:对于一般的分式混合运算来讲,其运算顺序与整式混合运算一样,是先乘方,再乘除,最后算加减,如果遇括号要先算括号里面的.
9、(2010 包头)化简,其结果是( )
A、 B、
C、 D、
考点:分式的混合运算。
分析:对于分式混合运算,其实也就是在同一个算式中,综合了分式的加减、乘除及乘方中的一种或几种运算,关键是要注意各种运算的先后顺序.
解答:解:原式=[+]×
=+)×,
=﹣,
=,
=,
=,
故选D.
点评:对于一般的分式混合运算来讲,其运算顺序与整式混合运算一样,是先乘方,再乘除,最后算加减,如果遇括号要先算括号里面的.在此基础上,有时也应该根据具体问题的特点,灵活应变,注意方法.
10、(2009 陕西)化简的结果是( )
A、a﹣b B、a+b
C、 D、
考点:分式的混合运算。
专题:计算题。
分析:先算括号里式子,再进行因式分解,最后进行分式的约分化简.
解答:解:==a+b,故选B.
点评:本题考查分式的运算,运算顺序是:先括号里,经过通分,再做乘法,约分化为最简.
11、(2009 黄冈)化简的结果是( )
A、﹣4 B、4
C、2a D、﹣2a
考点:分式的混合运算。
专题:计算题。
分析:由(a+b)c=ab+bc,运用分配律可约去各个分式的分母,使计算简便.
解答:解:原式=﹣(a+2)+(a﹣2)=﹣4,故选A.
点评:此题根据乘法的分配律先进行分式的乘法运算,然后再进行加减的运算,使运算简单化了,计算过程要注意符号间的变化.
12、(2009 定西)计算:=( )
A、 B、
C、 D、
考点:分式的混合运算。
专题:计算题。
分析:先算括号里式子,再把除法转化为乘法运算,最后进行分式的约分化简.
解答:解:==,故选A.
点评:注意此题的运算顺序:先括号里,经过通分,再把除法转化为乘法,约分化为最简.
13、(2008 临沂)化简(1+)的结果是( )
A、a+1 B、
C、 D、a﹣1
考点:分式的混合运算。
专题:计算题。
分析:先算括号里式子,再进行因式分解,最后把除法转化为乘法运算,进行分式的约分化简.
解答:解:(1+)==a﹣1.
故选D.
点评:当整式与分式相加减时,一般可以把整式看作分母为1的分式,与其它分式进行通分运算.
14、(2008 荆门)计算的结果是( )
A、 B、
C、a﹣b D、a+b
考点:分式的混合运算。
专题:计算题。
分析:先算小括号里的,再算乘法,约分化简即可.
解答:解:==,故选B.
点评:考查分式的化简,分式的化简关键在于通过通分、合并同类项、因式分解、约分转化为最简分式.
15、(2008 黄冈)计算的结果为( )
A、 B、
C、 D、
考点:分式的混合运算。
专题:计算题。
分析:先算小括号里的,再把除法统一成乘法,约分化为最简.
解答:解:==,故选A.
点评:分式的四则运算是整式四则运算的进一步发展,在计算时,首先要弄清楚运算顺序,先去括号,再进行分式的乘除.
16、(2007 威海)下列各式计算正确的是( )
A、 B、
C、 D、
考点:分式的混合运算;约分。
分析:按同底数幂除法法则,约分,分式混合运算法则进行运算,看结果是否正确即可.
解答:解:A、式应该为x3,错误;
B、分解正确;
C、的结果应该为﹣m﹣3,错误;
D、=,错误.
故选B.
点评:本题主要考查分式的混合运算,不是很难.
17、(2007 济南)计算的结果为( )
A、 B、
C、 D、
考点:分式的混合运算。
分析:先计算括号里的,再相乘.
解答:解:
=
=﹣
=﹣.
故选A.
点评:本题的关键是通分、分解因式、约分,用到了平方差公式.
18、(2006 武汉)计算(﹣a)÷(1﹣)的正确结果是( )
A、a﹣1 B、﹣a﹣1
C、1﹣a D、a+1
考点:分式的混合运算。
专题:计算题。
分析:先算括号里的通分,再进行因式分解,把除号换为乘号,最后再进行分式间的约分化简.
解答:解:原式==﹣a﹣1,故选B.
点评:注意混合运算时要先算括号里的,再算乘除.
19、(2006 温州)晓晓根据下表,作了三个推测:
x 1 10 100 1000 10000 …
3﹣ 3 2.1 2.01 2.001 2.0001 …
①3﹣(x>0)的值随着x的增大越来越小;
②3﹣(x>0)的值有可能等于2;
③3﹣(x>0)的值随着x的增大越来越接近于2.
则推测正确的有( )
A、0个 B、1个
C、2个 D、3个
考点:分式的混合运算。
专题:图表型。
分析:考查分式化简及混合运算.
解答:解:①观察式子3﹣,
可以看到分式可以化简为=﹣=1﹣,
所以,3﹣=3﹣(1﹣)=3﹣1+=2+.
当x>0时,会随着x的增大而减小.
所以,2+会随着x的增大而减小,故①对;
②分母不能为0,故的值不可能等于2,故②不对;
③又因为当x>0时,>0,所以2+>2,且会随着x的增大而越来越接近2,故正确.
故选C.
点评:此题考查分式的性质,注意分式的化简及因变量的取值与自变量的取值之间的联系.
20、(2006 黄冈)计算:的结果为( )
A、1 B、
C、 D、
考点:分式的混合运算。
专题:计算题。
分析:把第二个分式的分母先因式分解,再把除法统一成乘法,再算减法,化简即可.
解答:解:===1,故选A.
点评:此题要注意运算顺序,先乘除后加减,还要注意9﹣m2变形为﹣(m2﹣9).
二、填空题(共2小题)
21、(2011 泰安)化简:的结果为 x﹣6 .
考点:分式的混合运算。
专题:计算题。
分析:先将括号里面的通分合并同类项,然后将除法转换成乘法,约分化简得到最简代数式.
解答:解:原式=×
=×
=x﹣6
故答案为:x﹣6
点评:本题主要考查分式的混合运算,通分、因式分解和约分是解答的关键.
22、(2011 昆明)计算:= a .
考点:分式的混合运算。
分析:首先对括号内的式子通分相减,然后把除法转化为乘法,约分计算即可.
解答:解:原式=(+)
=
===a.
故答案是:a
点评:本题主要考查分式的混合运算,通分、因式分解和约分是解答的关键.
三、解答题(共8小题)
23、计算或化简:
(1)
(2)
(3)
(4).
考点:实数的运算;分式的混合运算。
分析:(1)根据绝对值的意义去掉绝对值的符号即可进行计算;
(2)根据负整数指数幂的规定和实数的计算法则进行计算;
(3)利用分式的计算法则进行计算;
(4)利用分式的计算法则和幂的定义进行计算.
解答:解:(1)原式=+2﹣+2=4﹣;
(2)原式=1﹣8﹣3+9=﹣1;
(3)原式===a+2;
(4)原式==.
点评:此题分别考查了绝对值的定义,实数的计算,幂的定义,分式的计算等知识,计算时一定要注意符号的处理.
24、计算:
(1)(﹣3a2b)2 (8a2b2);
(2)(x+2)2﹣(x+1)(x﹣1);
(3).
考点:整式的混合运算;分式的混合运算。
分析:(1)(2)考查了整式的混合运算;
(3)考查了分式的混合运算,整式与分式的混合运算的顺序都是先括号,再乘除.
解答:解:(1)原式=9a4b2 (8a2b2)=72a6b4;
(2)原式=x2+4x+4﹣x2+1=4x+5;
(3)原式=(﹣) = =.
点评:对于一般的分式混合运算来讲,其运算顺序与整式混合运算一样,是先乘方,再乘除,最后算加减,如果遇括号要先算括号里面的.在此基础上,有时也应该根据具体问题的特点,灵活应变,注意方法.
25、计算或化简:
(1)﹣4x3y[7x2y﹣3x2y3+(2x2y)3];
(2)(2x﹣3y)2﹣(x﹣2y)(x+2y);
(3)(x2x3)2÷(x3)2;
(4)1﹣.
考点:整式的混合运算;分式的混合运算。
专题:计算题。
分析:(1)主要考查了单项式与多项式的乘法;
(2)运用完全平方公式和平方差公式即可;
(3)底数不变,指数按运算法则计算即可;
(4)先通分再加减.
解答:解:(1)原式=﹣28x5y2+12x5y4﹣32x9y4;
(2)原式=4y2﹣12xy+9y2﹣x2+4y=23x2﹣12xy+13y2;
(3)原式=x10÷x6=x4;
(4)原式=1﹣×[×]=1﹣×=.
点评:此题主要考查了有理数的混合运算:首先要弄清楚运算顺序,先去括号,再进行有理数的乘除,最后是加减.
26、计算或化简:
(1)﹣2x2y[(﹣2xy2)3+1];
(2)(2a+b)2﹣(a+2b)(a﹣2b);
(3)(﹣y3 y)2÷(﹣y)2;
(4)﹣x+y.
考点:整式的混合运算;分式的混合运算。
专题:计算题。
分析:根据整式的运算法则和分式的运算法则进行计算.
解答:解:(1)原式=16x5y7﹣2x2y;
(2)原式=4a2+4ab+b2﹣a2+4b=3a2+4ab+5b2;
(3)原式=y6;
(4)原式==.
点评:本题主要考查分式和整式的运算,注意运算顺序.
27、化简下列各式:
(1)z
(2)
(3)[(2x+y)2﹣y(y+4x)﹣8x]÷2x
(4).
考点:整式的混合运算;分式的混合运算。
专题:计算题。
分析:有理数的混合运算首先要弄清楚运算顺序,先去括号,再进行有理数的乘除,最后是加减.
解答:解:
(1)原式=x3y3z;
(2)原式=2a3b2﹣a2b3;
(3)原式=(4x2+4xy+y2﹣y2﹣4xy﹣8x)÷2x=2x﹣4;
(4)原式=×=2x﹣4.
故答案为x3y3z.
点评:规律总结:对于一般的分式混合运算来讲,其运算顺序与整式混合运算一样,是先乘方,再乘除,最后算加减,如果遇括号要先算括号里面的.在此基础上,有时也应该根据具体问题的特点,灵活应变,注意方法.
28、化简:
(1)
(2)
考点:分式的乘除法;分式的混合运算。
专题:计算题。
分析:(1)是分式的加法运算,先化为同分母分式,然后根据分式的加减法法则进行运算.
(2)是分式加减乘除混合运算,计算时应先算乘除,后算加减,有括号,先算括号里面的.
解答:解:(1)原式===;
(2)原式===4.
点评:对于分式运算,若是加减运算,先把异分母化为同分母,再进行计算.若是加减乘除混合运算,应注意先因式分解,再约分,并且各种运算的结果必须是最简分式.
29、计算
(1)÷
(2)÷
考点:分式的乘除法;分式的混合运算。
专题:计算题。
分析:(1)首先把除法运算转化成乘法运算,然后因式分解因式进行约分.(2)乘方的运用,注意符号.
解答:解:(1)原式=
=2x x
=
(2)原式=
=﹣.
点评:在分式的乘除运算中,除了准确运用分式的运算法则外,还要灵活运用因式分解和乘方法则.
30、(2011 玉溪)化简:() (x2﹣9).
考点:分式的混合运算。
分析:先把(x2﹣9)分解为(x+3)(x﹣3),再利用乘法的分配律分别与括号里的各项相乘,最后去括号合并同类项即可.
解答:解:() (x2﹣9)
=
=x(x﹣3)﹣(x+3)
=x2﹣3x﹣x﹣3
=x2﹣4x﹣3.
点评:此题考查了分式的混合运算,解题时要注意简便方法的应用.
