16.2.1分式的乘除法的专题训练(附答案及解析)
文档属性
| 名称 | 16.2.1分式的乘除法的专题训练(附答案及解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 175.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-16 00:00:00 | ||
图片预览

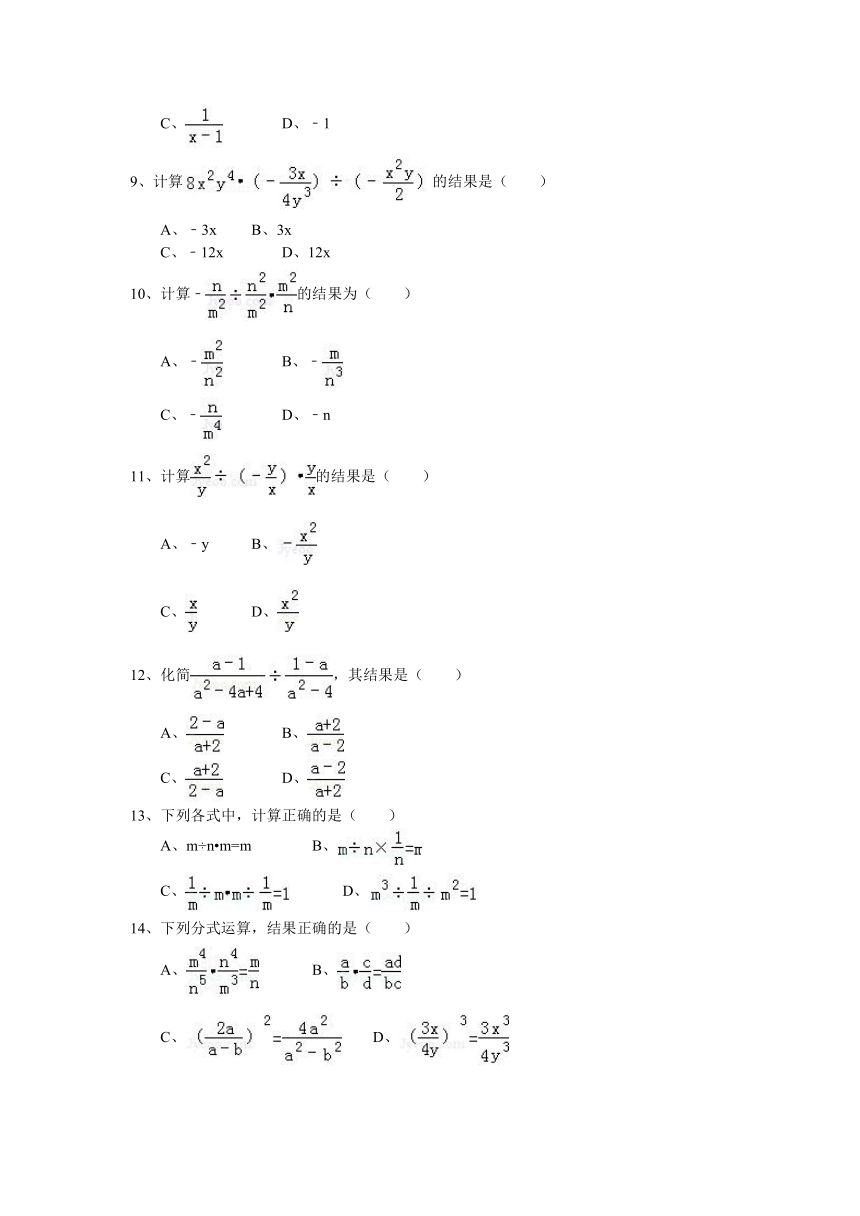



文档简介
分式的乘除法 专题训练
一、选择题(共20小题)
1、下列计算正确的是( )
A、2a2+3a3=5a5 B、
C、(﹣2a3)3=﹣6a9 D、
2、(2011 眉山)化简的结果是( )
A、﹣m﹣1 B、﹣m+1
C、﹣mn+m D、﹣mn﹣n
3、(2010 威海)化简的结果是( )
A、﹣a﹣1 B、﹣a+1
C、﹣ab+1 D、﹣ab+b
4、(2010 苏州)化简的结果是( )
A、 B、a
C、a﹣1 D、
5、(2009 昆明)下列运算正确的是( )
A、=±4 B、2a+3b=5ab
C、(x﹣3)2=x2﹣9 D、(﹣)2=
6、(2008 昆明)下列运算中,正确的是( )
A、2+=2 B、(x+2y)2=x2+4y2
C、x8÷x4=x2 D、
7、(2007 安徽)化简(﹣)÷的结果是( )
A、﹣x﹣1 B、﹣x+1
C、﹣ D、
8、(2000 武汉)计算所得正确结果( )
A、 B、1
C、 D、﹣1
9、计算的结果是( )
A、﹣3x B、3x
C、﹣12x D、12x
10、计算﹣的结果为( )
A、﹣ B、﹣
C、﹣ D、﹣n
11、计算的结果是( )
A、﹣y B、
C、 D、
12、化简,其结果是( )
A、 B、
C、 D、
13、下列各式中,计算正确的是( )
A、m÷n m=m B、
C、 D、
14、下列分式运算,结果正确的是( )
A、 B、
C、 D、
15、若分式÷的值等于5,则a的值是( )
A、5 B、﹣5
C、 D、﹣
16、计算的值等于( )
A、﹣9a B、9a
C、﹣36a D、36a
17、下列各式计算正确的是( )
A、x÷y =x B、x y÷x y=1
C、÷ =1 D、x2÷÷x=1
18、下列计算中,错误的是( )
A、 B、
C、 D、
19、化简x÷等于( )
A、1 B、xy
C、 D、
20、计算得( )
A、x5 B、x5y
C、y5 D、xy5
二、填空题(共6小题)
21、已知M=,那么M,N的大小关系是 _________ .(填“>”或“<”)
22、(a2m+3am+2)÷(am+1)= _________ .
23、多项式4x2+4x+1分解因式的结果是 _________ ;计算的结果是 _________
24、,( )= _________ ;
= _________ ;
25、①分式与的最简公分母是 _________ ;
②分式的值为零的条件是 _________ ;
③计算(xy﹣x2) = _________ .
26、(2011 聊城)化简:÷= _________ .
三、解答题(共2小题)
27、给定下面一列分式:,(其中x≠0)
(1)把任意一个分式除以前面一个分式,你发现了什么规律?
(2)根据你发现的规律,试写出给定的那列分式中的第7个分式.
28、(1)已知恒等式x3﹣x2﹣x+1=(x﹣1)(x2+kx﹣1),求k的值;
(2)若x是整数,求证:是整数.
答案与评分标准
一、选择题(共20小题)
1、下列计算正确的是( )
A、2a2+3a3=5a5 B、
C、(﹣2a3)3=﹣6a9 D、
考点:整式的加减;幂的乘方与积的乘方;分式的乘除法。
专题:计算题。
分析:此题考查整式的加减,幂的乘方与积的乘方及分式的除法运算.
解答:解:A、2a2+3a3≠5a2,A错;
B、=a4,B错;
C、(﹣2a3)3=﹣8a9,C错;
D、=,D正确,
故选D.
点评:本题主要考查整式的加减,幂的乘方与积的乘方及分式的除法等简单的计算问题.
2、(2011 眉山)化简的结果是( )
A、﹣m﹣1 B、﹣m+1
C、﹣mn+m D、﹣mn﹣n
考点:分式的乘除法。
专题:探究型。
分析:根据分式乘法及除法的运算法则进行计算,即分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘.
解答:解:原式=(﹣)×=﹣m+1.
故选B.
点评:本题考查的是分式的乘除法,分式乘除法的运算,归根到底是乘法的运算,当分子和分母是多项式时,一般应先进行因式分解,再约分.
3、(2010 威海)化简的结果是( )
A、﹣a﹣1 B、﹣a+1
C、﹣ab+1 D、﹣ab+b
考点:分式的乘除法。
分析:本题考查的是分式的除法运算,做除法运算时要转化为乘法的运算,注意先把分子、分母能因式分解的先分解,然后约分.
解答:解:=(﹣)×=﹣a+1.
故选B.
点评:分式乘除法的运算,归根到底是乘法的运算,当分子和分母是多项式时,一般应先进行因式分解,再约分.
4、(2010 苏州)化简的结果是( )
A、 B、a
C、a﹣1 D、
考点:分式的乘除法。
分析:本题考查的是分式的除法运算,做除法运算时要转化为乘法的运算,注意先把分子、分母能因式分解的先分解,然后约分.
解答:解:=×=a.
故选B.
点评:分式乘除法的运算,归根到底是乘法的运算,当分子和分母是多项式时,一般应先进行因式分解,再约分.
5、(2009 昆明)下列运算正确的是( )
A、=±4 B、2a+3b=5ab
C、(x﹣3)2=x2﹣9 D、(﹣)2=
考点:分式的乘除法;算术平方根;合并同类项;完全平方公式。
分析:本题根据算术平方根、合并同类项、完全平方式、分式的乘除法等知识点进行判断.
解答:解:A、=4,因此A的结论是错误的;
B、2a+3b没有同类项,不能合并;
C、(x﹣3)2=x2﹣6x+9;
D、(﹣)2=,正确;
故选D.
点评:本题考查了分式的乘除法、算术平方根、合并同类项、完全平方公式等知识.
6、(2008 昆明)下列运算中,正确的是( )
A、2+=2 B、(x+2y)2=x2+4y2
C、x8÷x4=x2 D、
考点:分式的乘除法;实数的运算;同底数幂的除法;完全平方公式。
分析:本题根据分式的乘除法、实数的运算、同底数幂的除法、完全平方式等知识点进行判断.
解答:解:A、由于2和不是同类二次根式,因此不能合并,
B、根据公式将式子展开即可判断,原式错误,
C、同底数幂相除,底数不变指数相减,故x8÷x4=x4,
D、先将除法转化为乘法,然后将各分式的分子、分母分解因式,进而可通过约分、化简得出结果正确.
故选D.
点评:本题主要考查了同底数幂的运算,完全平方公式,以及分式的除法运算的方法.
7、(2007 安徽)化简(﹣)÷的结果是( )
A、﹣x﹣1 B、﹣x+1
C、﹣ D、
考点:分式的乘除法。
分析:在完成此类化简题时,应先将分子、分母中能够分解因式的部分进行分解因式.有些需要先提取公因式,而有些则需要运用公式法进行分解因式.通过分解因式,把分子分母中能够分解因式的部分,分解成乘积的形式,然后找到其中的公因式约去.
解答:解:(﹣)÷,
=(﹣)×,
=﹣(x+1),
=﹣x﹣1.
故选A.
点评:分式的乘除混合运算一般是统一为乘法运算,如果有乘方,还应根据分式乘方法则先乘方,即把分子、分母分别乘方,然后再进行乘除运算.同样要注意的地方有:一是要确定好结果的符号;二是运算顺序不能颠倒.
8、(2000 武汉)计算所得正确结果( )
A、 B、1
C、 D、﹣1
考点:分式的乘除法。
分析:本题考查的是分式的除法运算,做除法运算时,先把除法转化成乘法,要注意先把分子、分母能因式分解的先分解,然后约分.
解答:解:原式===,故选A.
点评:在完成此类化简题时,应先将分子、分母中能够分解因式的部分进行分解因式.有些需要先提取公因式,而有些则需要运用公式法进行分解因式.通过分解因式,把分子分母中能够分解因式的部分,分解成乘积的形式,然后找到其中的公因式约去.
9、计算的结果是( )
A、﹣3x B、3x
C、﹣12x D、12x
考点:分式的乘除法。
分析:在进行分式乘方运算时,先确定运算结果的符号,负数的偶数次方为正,而奇数次方为负,同时要注意运算顺序,先乘方,后乘除.
解答:解:原式=×=12x;
故选D.
点评:分式的乘除混合运算一般是统一为乘法运算,如果有乘方,还应根据分式乘方法则先乘方,即把分子、分母分别乘方,然后再进行乘除运算.同样要注意的地方有:一是要确定好结果的符号;二是运算顺序不能颠倒.
10、计算﹣的结果为( )
A、﹣ B、﹣
C、﹣ D、﹣n
考点:分式的乘除法。
分析:在进行分式乘方运算时,先确定运算结果的符号,同时要注意运算顺序,先乘方,后乘除.
解答:解:
=
=﹣;
故选A.
点评:分式的乘除混合运算一般是统一为乘法运算,如果有乘方,还应根据分式乘方法则先乘方,即把分子、分母分别乘方,然后再进行乘除运算.同样要注意的地方有:一是要确定好结果的符号;二是运算顺序不能颠倒.
11、计算的结果是( )
A、﹣y B、
C、 D、
考点:分式的乘除法。
分析:分式的运算首先要分清运算顺序,在这个题目中,首先进行乘方运算,然后统一成乘法运算,最后进行约分运算.
解答:解:原式=.
故选B.
点评:在计算过程中需要注意的是运算顺序.分式的乘除运算实际就是分式的约分.
12、化简,其结果是( )
A、 B、
C、 D、
考点:分式的乘除法。
分析:在完成此类化简题时,应先将分子、分母中能够分解因式的部分进行分解因式.有些需要先提取公因式,而有些则需要运用公式法进行分解因式.通过分解因式,把分子分母中能够分解因式的部分,分解成乘积的形式,然后找到其中的公因式约去.
解答:解:
=×,
=.
因此选择C.
点评:分式的乘除混合运算一般是统一为乘法运算,如果有乘方,还应根据分式乘方法则先乘方,即把分子、分母分别乘方,然后再进行乘除运算.
13、下列各式中,计算正确的是( )
A、m÷n m=m B、
C、 D、
考点:分式的乘除法。
分析:本题考查的是分式的乘除法运算.可先将分式的乘除运算统一为乘法运算,然后将各分式的分子、分母分解因式,进而可通过约分、化简得出结果.
解答:解:A、原式=;
B、原式=;
C、原式=;
D、原式=;所以只有C选项是正确的.
故选C.
点评:分式的乘除混合运算一般是统一为乘法运算,如果有乘方,还应根据分式乘方法则先乘方,即把分子、分母分别乘方,然后再进行乘除运算.同样要注意的地方有:一是要确定好结果的符号;二是运算顺序不能颠倒.
14、下列分式运算,结果正确的是( )
A、 B、
C、 D、
考点:分式的乘除法。
分析:分式的乘除混合运算一般是统一为乘法运算,如果有乘方,还应根据分式乘方法则先乘方,即把分子、分母分别乘方,然后再进行乘除运算.同样要注意的地方有:一是要确定好结果的符号;二是运算顺序不能颠倒.
解答:解:A、;
B、原式=;
C、原式=;
D、原式=;
故选A.
点评:在进行分式乘方运算时,先确定运算结果的符号,负数的偶数次方为正,而奇数次方为负,同时要注意运算顺序,先乘方,后乘除.
15、若分式÷的值等于5,则a的值是( )
A、5 B、﹣5
C、 D、﹣
考点:分式的乘除法。
专题:计算题。
分析:首先根据分式的除法法则计算÷,然后根据题意列出方程,从而求出a的值.
解答:解:∵÷= =,
∴=5,
∴a=.
故选C.
点评:本题主要考查了分式的除法法则.将分式的除法转化为乘法以后,注意将分子、分母分解因式,然后约分化简.
16、计算的值等于( )
A、﹣9a B、9a
C、﹣36a D、36a
考点:分式的乘除法。
分析:计算时首先要把乘除运算转化成乘法运算,在计算的过程中要注意符号的变化.
解答:解:原式==36a,
故选D.
点评:运算过程中首先要确定符号,然后把乘除的混合运算转化成乘法运算,进行约分运算.
17、下列各式计算正确的是( )
A、x÷y =x B、x y÷x y=1
C、÷ =1 D、x2÷÷x=1
考点:分式的乘除法。
分析:本题可根据分式的乘除法法则进行计算,进而可判断出正确的选项.
解答:解:A、原式=;
B、原式=;
C、原式=;
D、原式=;
故选C.
点评:分式的乘除混合运算一般是统一为乘法运算,如果有乘方,还应根据分式乘方法则先乘方,即把分子、分母分别乘方,然后再进行乘除运算.同样要注意的地方有:一是要确定好结果的符号;二是运算顺序不能颠倒.
18、下列计算中,错误的是( )
A、 B、
C、 D、
考点:分式的乘除法。
分析:本题在进行分式乘方运算时,先确定运算结果的符号,负数的偶数次方为正,而奇数次方为负,同时要注意运算顺序,先乘方,后乘除.
解答:解:A、,正确,
B、,正确,
C、,原式错误,
D、,正确,
故选C.
点评:分式的乘除混合运算一般是统一为乘法运算,如果有乘方,还应根据分式乘方法则先乘方,即把分子、分母分别乘方,然后再进行乘除运算.同样要注意的地方有:一是要确定好结果的符号;二是运算顺序不能颠倒.
19、化简x÷等于( )
A、1 B、xy
C、 D、
考点:分式的乘除法。
分析:分式的乘除运算,首先要统一成乘法运算,然后进行约分.在计算中要注意运算顺序,乘除运算从左到右依次计算.
解答:解:原式=x ==.
故选C.
点评:分式的乘除混合运算转化成乘法运算是解决的关键.本题易出现的错误是直接将后两项合并化简,因此要特别注意运算的顺序不能乱.
20、计算得( )
A、x5 B、x5y
C、y5 D、xy5
考点:分式的乘除法。
分析:分式的运算首先要分清运算顺序,在这个题目中,首先进行乘方运算,然后统一成乘法运算,最后进行约分运算.
解答:解:原式=,
故选A.
点评:在计算过程中需要注意的是运算顺序.并且这类计算最终转化为约分运算.
二、填空题(共6小题)
21、已知M=,那么M,N的大小关系是 M>N .(填“>”或“<”)
考点:有理数大小比较;分式的乘除法。
专题:整体思想;换元法。
分析:先令21998=n,再运用作商法得出M÷N>1,从而得出M,N的大小关系.
解答:解:令21998=n,则21999=2 21998=2n,22000=4n,
∴M÷N=÷=.
∴M>N.
故答案为:M>N.
点评:本题考查了分数的大小比较,难度较大.本题采取换元作商法大大降低了计算量,且不容易出错.
22、(a2m+3am+2)÷(am+1)= am+2 .
考点:整式的除法;因式分解-十字相乘法等;分式的乘除法。
专题:计算题;整体思想;因式分解。
分析:题目是多项式除以多项式,可先将被除式中的多项式a2m+3am+2分解因式,再根据分式的除法法则进行计算.
解答:解:∵a2m+3am+2,
=(am)2+3(am)+2,
=(am+2)(am+1),
∴(a2m+3am+2)÷(am+1),
=,
=am+2.
故答案为:am+2.
点评:本题主要考查了运用十字相乘法分解因式a2m+3am+2及根据分式的基本性质进行分式的约分.多项式除以多项式的内容在初中教材大纲中不学习,本题属于竞赛题型,有一定难度.本题的关键是想到将被除式a2m+3am+2分解因式,难点是将am看作一个字母,则它是关于这个字母的二次三项式,因此可以运用十字相乘法分解因式.
23、多项式4x2+4x+1分解因式的结果是 (2x+1)2 ;计算的结果是
考点:因式分解-运用公式法;分式的乘除法。
分析:①用完全平方公式分解即可;
②把除法统一为乘法,再约分、化简即可.
解答:解:①4x2+4x+1=(2x+1)2;
②÷2xb=×=.
点评:整个式子为三项,有两项平方项,一项为平方项的底数的积的±2倍时,应考虑运用完全平方公式进行分解;分式的除法应统一为乘法后再进行计算.
24、,( )= xy2 ;
= ﹣ ;
考点:分式的基本性质;分式的乘除法。
分析:(1)根据分式的基本性质把的分母化为x2y的形式即可;
(2)找出分子、分母的公因式,把分子、分母同时除以其公因式即可.
解答:解:(1)∵把的分子、分母同时乘以xy得,==,
∴( )=xy2.
(2)∵分式中分子、分母的公因式为4abc3,
∴=﹣.
点评:本题考查的是分式的基本性质,即分式的分子、分母同时乘以或除以一个不为0的数,分式的值不变.
25、①分式与的最简公分母是 x(x+3)(x﹣3) ;
②分式的值为零的条件是 a=1且a≠﹣1 ;
③计算(xy﹣x2) = x2y .
考点:最简公分母;分式的值为零的条件;分式的乘除法。
分析:利用分式的混合运算法则计算即可.
解答:解:①两个分式的分母可分解为x(x﹣3),(x+3)(x﹣3),所以最简公分母是x(x+3)(x﹣3);
②此分式的值为0的条件是分子a﹣1=0,而分母b+1≠0,即a=1,b≠﹣1;
③(xy﹣x2) =﹣x(x﹣y) =x2y.
点评:①考查了确定最简公分母的方法;②考查了分式为0时的条件;③考查了简单的分式计算.
26、(2011 聊城)化简:÷= .
考点:分式的乘除法。
分析:首先分解每个因式的分子与分母,把除法转化成乘法,然后约分即可求解.
解答:解:原式= =.
故答案为:
点评:本题考查了分式的化简,正确对分子、分母分解因式是关键.
三、解答题(共2小题)
27、给定下面一列分式:,(其中x≠0)
(1)把任意一个分式除以前面一个分式,你发现了什么规律?
(2)根据你发现的规律,试写出给定的那列分式中的第7个分式.
考点:规律型:数字的变化类;分式的基本性质;分式的乘除法。
专题:规律型。
分析:(1)将任意一个分式除以前面一个分式,可得出规律.
(2)由(1)可知任意一个分式除以前面一个分式恒等于一个代数式,由此可得出第7个分式.
解答:解:(1)第二个分式除以第一个分式得﹣,第三个分式除以第二个分式得﹣,
同理,第四个分式除以第三个分式也是﹣,故规律是任意一个分式除以前面一个分式;
(2)由(1)可知该第7个分式应该是×=.
点评:本题涉及数字的变化及数列的相关知识,根据题干的规律能找到一般表达式,难度中等.
28、(1)已知恒等式x3﹣x2﹣x+1=(x﹣1)(x2+kx﹣1),求k的值;
(2)若x是整数,求证:是整数.
考点:多项式乘多项式;因式分解-运用公式法;分式的乘除法;解一元一次方程。
专题:计算题;方程思想。
分析:(1)先将等式右边展开计算,再根据多项式恒等的性质,两边对应项系数相等,列出关于k的方程,从而求出k的值;
(2)把(1)中k的值代入,可将x3﹣x2﹣x+1因式分解,再进行分式的除法运算,可求出的结果,然后根据条件x是整数,即可得证.
解答:解:(1)由题设知,(x﹣1)(x2+kx﹣1)=x3+(k﹣1)x2﹣(k+1)x+1,
所以x3﹣x2﹣x+1=x3+(k﹣1)x2﹣(k+1)x+1,
从而有k﹣1=﹣1,﹣k﹣1=﹣1,
解得k=0.
故所求k的值为0;
(2)由(1)知k=0,则x3﹣x2﹣x+1=(x﹣1)(x2﹣1)=(x﹣1)2(x+1),
∴==x+1.
又∵x是整数,
∴x+1是整数.
故是整数.
点评:本题主要考查了多项式乘多项式的法则,因式分解及分式的除法.由于多项式除以多项式的内容在初中教材大纲中不学习,故本题第二问有一定难度,属于竞赛题型.解决第一问的关键是根据多项式乘多项式的法则,利用两边对应项系数相等,列出关于k的方程;解决第二问的关键是利用(1)的结论,将多项式x3﹣x2﹣x+1因式分解.
一、选择题(共20小题)
1、下列计算正确的是( )
A、2a2+3a3=5a5 B、
C、(﹣2a3)3=﹣6a9 D、
2、(2011 眉山)化简的结果是( )
A、﹣m﹣1 B、﹣m+1
C、﹣mn+m D、﹣mn﹣n
3、(2010 威海)化简的结果是( )
A、﹣a﹣1 B、﹣a+1
C、﹣ab+1 D、﹣ab+b
4、(2010 苏州)化简的结果是( )
A、 B、a
C、a﹣1 D、
5、(2009 昆明)下列运算正确的是( )
A、=±4 B、2a+3b=5ab
C、(x﹣3)2=x2﹣9 D、(﹣)2=
6、(2008 昆明)下列运算中,正确的是( )
A、2+=2 B、(x+2y)2=x2+4y2
C、x8÷x4=x2 D、
7、(2007 安徽)化简(﹣)÷的结果是( )
A、﹣x﹣1 B、﹣x+1
C、﹣ D、
8、(2000 武汉)计算所得正确结果( )
A、 B、1
C、 D、﹣1
9、计算的结果是( )
A、﹣3x B、3x
C、﹣12x D、12x
10、计算﹣的结果为( )
A、﹣ B、﹣
C、﹣ D、﹣n
11、计算的结果是( )
A、﹣y B、
C、 D、
12、化简,其结果是( )
A、 B、
C、 D、
13、下列各式中,计算正确的是( )
A、m÷n m=m B、
C、 D、
14、下列分式运算,结果正确的是( )
A、 B、
C、 D、
15、若分式÷的值等于5,则a的值是( )
A、5 B、﹣5
C、 D、﹣
16、计算的值等于( )
A、﹣9a B、9a
C、﹣36a D、36a
17、下列各式计算正确的是( )
A、x÷y =x B、x y÷x y=1
C、÷ =1 D、x2÷÷x=1
18、下列计算中,错误的是( )
A、 B、
C、 D、
19、化简x÷等于( )
A、1 B、xy
C、 D、
20、计算得( )
A、x5 B、x5y
C、y5 D、xy5
二、填空题(共6小题)
21、已知M=,那么M,N的大小关系是 _________ .(填“>”或“<”)
22、(a2m+3am+2)÷(am+1)= _________ .
23、多项式4x2+4x+1分解因式的结果是 _________ ;计算的结果是 _________
24、,( )= _________ ;
= _________ ;
25、①分式与的最简公分母是 _________ ;
②分式的值为零的条件是 _________ ;
③计算(xy﹣x2) = _________ .
26、(2011 聊城)化简:÷= _________ .
三、解答题(共2小题)
27、给定下面一列分式:,(其中x≠0)
(1)把任意一个分式除以前面一个分式,你发现了什么规律?
(2)根据你发现的规律,试写出给定的那列分式中的第7个分式.
28、(1)已知恒等式x3﹣x2﹣x+1=(x﹣1)(x2+kx﹣1),求k的值;
(2)若x是整数,求证:是整数.
答案与评分标准
一、选择题(共20小题)
1、下列计算正确的是( )
A、2a2+3a3=5a5 B、
C、(﹣2a3)3=﹣6a9 D、
考点:整式的加减;幂的乘方与积的乘方;分式的乘除法。
专题:计算题。
分析:此题考查整式的加减,幂的乘方与积的乘方及分式的除法运算.
解答:解:A、2a2+3a3≠5a2,A错;
B、=a4,B错;
C、(﹣2a3)3=﹣8a9,C错;
D、=,D正确,
故选D.
点评:本题主要考查整式的加减,幂的乘方与积的乘方及分式的除法等简单的计算问题.
2、(2011 眉山)化简的结果是( )
A、﹣m﹣1 B、﹣m+1
C、﹣mn+m D、﹣mn﹣n
考点:分式的乘除法。
专题:探究型。
分析:根据分式乘法及除法的运算法则进行计算,即分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘.
解答:解:原式=(﹣)×=﹣m+1.
故选B.
点评:本题考查的是分式的乘除法,分式乘除法的运算,归根到底是乘法的运算,当分子和分母是多项式时,一般应先进行因式分解,再约分.
3、(2010 威海)化简的结果是( )
A、﹣a﹣1 B、﹣a+1
C、﹣ab+1 D、﹣ab+b
考点:分式的乘除法。
分析:本题考查的是分式的除法运算,做除法运算时要转化为乘法的运算,注意先把分子、分母能因式分解的先分解,然后约分.
解答:解:=(﹣)×=﹣a+1.
故选B.
点评:分式乘除法的运算,归根到底是乘法的运算,当分子和分母是多项式时,一般应先进行因式分解,再约分.
4、(2010 苏州)化简的结果是( )
A、 B、a
C、a﹣1 D、
考点:分式的乘除法。
分析:本题考查的是分式的除法运算,做除法运算时要转化为乘法的运算,注意先把分子、分母能因式分解的先分解,然后约分.
解答:解:=×=a.
故选B.
点评:分式乘除法的运算,归根到底是乘法的运算,当分子和分母是多项式时,一般应先进行因式分解,再约分.
5、(2009 昆明)下列运算正确的是( )
A、=±4 B、2a+3b=5ab
C、(x﹣3)2=x2﹣9 D、(﹣)2=
考点:分式的乘除法;算术平方根;合并同类项;完全平方公式。
分析:本题根据算术平方根、合并同类项、完全平方式、分式的乘除法等知识点进行判断.
解答:解:A、=4,因此A的结论是错误的;
B、2a+3b没有同类项,不能合并;
C、(x﹣3)2=x2﹣6x+9;
D、(﹣)2=,正确;
故选D.
点评:本题考查了分式的乘除法、算术平方根、合并同类项、完全平方公式等知识.
6、(2008 昆明)下列运算中,正确的是( )
A、2+=2 B、(x+2y)2=x2+4y2
C、x8÷x4=x2 D、
考点:分式的乘除法;实数的运算;同底数幂的除法;完全平方公式。
分析:本题根据分式的乘除法、实数的运算、同底数幂的除法、完全平方式等知识点进行判断.
解答:解:A、由于2和不是同类二次根式,因此不能合并,
B、根据公式将式子展开即可判断,原式错误,
C、同底数幂相除,底数不变指数相减,故x8÷x4=x4,
D、先将除法转化为乘法,然后将各分式的分子、分母分解因式,进而可通过约分、化简得出结果正确.
故选D.
点评:本题主要考查了同底数幂的运算,完全平方公式,以及分式的除法运算的方法.
7、(2007 安徽)化简(﹣)÷的结果是( )
A、﹣x﹣1 B、﹣x+1
C、﹣ D、
考点:分式的乘除法。
分析:在完成此类化简题时,应先将分子、分母中能够分解因式的部分进行分解因式.有些需要先提取公因式,而有些则需要运用公式法进行分解因式.通过分解因式,把分子分母中能够分解因式的部分,分解成乘积的形式,然后找到其中的公因式约去.
解答:解:(﹣)÷,
=(﹣)×,
=﹣(x+1),
=﹣x﹣1.
故选A.
点评:分式的乘除混合运算一般是统一为乘法运算,如果有乘方,还应根据分式乘方法则先乘方,即把分子、分母分别乘方,然后再进行乘除运算.同样要注意的地方有:一是要确定好结果的符号;二是运算顺序不能颠倒.
8、(2000 武汉)计算所得正确结果( )
A、 B、1
C、 D、﹣1
考点:分式的乘除法。
分析:本题考查的是分式的除法运算,做除法运算时,先把除法转化成乘法,要注意先把分子、分母能因式分解的先分解,然后约分.
解答:解:原式===,故选A.
点评:在完成此类化简题时,应先将分子、分母中能够分解因式的部分进行分解因式.有些需要先提取公因式,而有些则需要运用公式法进行分解因式.通过分解因式,把分子分母中能够分解因式的部分,分解成乘积的形式,然后找到其中的公因式约去.
9、计算的结果是( )
A、﹣3x B、3x
C、﹣12x D、12x
考点:分式的乘除法。
分析:在进行分式乘方运算时,先确定运算结果的符号,负数的偶数次方为正,而奇数次方为负,同时要注意运算顺序,先乘方,后乘除.
解答:解:原式=×=12x;
故选D.
点评:分式的乘除混合运算一般是统一为乘法运算,如果有乘方,还应根据分式乘方法则先乘方,即把分子、分母分别乘方,然后再进行乘除运算.同样要注意的地方有:一是要确定好结果的符号;二是运算顺序不能颠倒.
10、计算﹣的结果为( )
A、﹣ B、﹣
C、﹣ D、﹣n
考点:分式的乘除法。
分析:在进行分式乘方运算时,先确定运算结果的符号,同时要注意运算顺序,先乘方,后乘除.
解答:解:
=
=﹣;
故选A.
点评:分式的乘除混合运算一般是统一为乘法运算,如果有乘方,还应根据分式乘方法则先乘方,即把分子、分母分别乘方,然后再进行乘除运算.同样要注意的地方有:一是要确定好结果的符号;二是运算顺序不能颠倒.
11、计算的结果是( )
A、﹣y B、
C、 D、
考点:分式的乘除法。
分析:分式的运算首先要分清运算顺序,在这个题目中,首先进行乘方运算,然后统一成乘法运算,最后进行约分运算.
解答:解:原式=.
故选B.
点评:在计算过程中需要注意的是运算顺序.分式的乘除运算实际就是分式的约分.
12、化简,其结果是( )
A、 B、
C、 D、
考点:分式的乘除法。
分析:在完成此类化简题时,应先将分子、分母中能够分解因式的部分进行分解因式.有些需要先提取公因式,而有些则需要运用公式法进行分解因式.通过分解因式,把分子分母中能够分解因式的部分,分解成乘积的形式,然后找到其中的公因式约去.
解答:解:
=×,
=.
因此选择C.
点评:分式的乘除混合运算一般是统一为乘法运算,如果有乘方,还应根据分式乘方法则先乘方,即把分子、分母分别乘方,然后再进行乘除运算.
13、下列各式中,计算正确的是( )
A、m÷n m=m B、
C、 D、
考点:分式的乘除法。
分析:本题考查的是分式的乘除法运算.可先将分式的乘除运算统一为乘法运算,然后将各分式的分子、分母分解因式,进而可通过约分、化简得出结果.
解答:解:A、原式=;
B、原式=;
C、原式=;
D、原式=;所以只有C选项是正确的.
故选C.
点评:分式的乘除混合运算一般是统一为乘法运算,如果有乘方,还应根据分式乘方法则先乘方,即把分子、分母分别乘方,然后再进行乘除运算.同样要注意的地方有:一是要确定好结果的符号;二是运算顺序不能颠倒.
14、下列分式运算,结果正确的是( )
A、 B、
C、 D、
考点:分式的乘除法。
分析:分式的乘除混合运算一般是统一为乘法运算,如果有乘方,还应根据分式乘方法则先乘方,即把分子、分母分别乘方,然后再进行乘除运算.同样要注意的地方有:一是要确定好结果的符号;二是运算顺序不能颠倒.
解答:解:A、;
B、原式=;
C、原式=;
D、原式=;
故选A.
点评:在进行分式乘方运算时,先确定运算结果的符号,负数的偶数次方为正,而奇数次方为负,同时要注意运算顺序,先乘方,后乘除.
15、若分式÷的值等于5,则a的值是( )
A、5 B、﹣5
C、 D、﹣
考点:分式的乘除法。
专题:计算题。
分析:首先根据分式的除法法则计算÷,然后根据题意列出方程,从而求出a的值.
解答:解:∵÷= =,
∴=5,
∴a=.
故选C.
点评:本题主要考查了分式的除法法则.将分式的除法转化为乘法以后,注意将分子、分母分解因式,然后约分化简.
16、计算的值等于( )
A、﹣9a B、9a
C、﹣36a D、36a
考点:分式的乘除法。
分析:计算时首先要把乘除运算转化成乘法运算,在计算的过程中要注意符号的变化.
解答:解:原式==36a,
故选D.
点评:运算过程中首先要确定符号,然后把乘除的混合运算转化成乘法运算,进行约分运算.
17、下列各式计算正确的是( )
A、x÷y =x B、x y÷x y=1
C、÷ =1 D、x2÷÷x=1
考点:分式的乘除法。
分析:本题可根据分式的乘除法法则进行计算,进而可判断出正确的选项.
解答:解:A、原式=;
B、原式=;
C、原式=;
D、原式=;
故选C.
点评:分式的乘除混合运算一般是统一为乘法运算,如果有乘方,还应根据分式乘方法则先乘方,即把分子、分母分别乘方,然后再进行乘除运算.同样要注意的地方有:一是要确定好结果的符号;二是运算顺序不能颠倒.
18、下列计算中,错误的是( )
A、 B、
C、 D、
考点:分式的乘除法。
分析:本题在进行分式乘方运算时,先确定运算结果的符号,负数的偶数次方为正,而奇数次方为负,同时要注意运算顺序,先乘方,后乘除.
解答:解:A、,正确,
B、,正确,
C、,原式错误,
D、,正确,
故选C.
点评:分式的乘除混合运算一般是统一为乘法运算,如果有乘方,还应根据分式乘方法则先乘方,即把分子、分母分别乘方,然后再进行乘除运算.同样要注意的地方有:一是要确定好结果的符号;二是运算顺序不能颠倒.
19、化简x÷等于( )
A、1 B、xy
C、 D、
考点:分式的乘除法。
分析:分式的乘除运算,首先要统一成乘法运算,然后进行约分.在计算中要注意运算顺序,乘除运算从左到右依次计算.
解答:解:原式=x ==.
故选C.
点评:分式的乘除混合运算转化成乘法运算是解决的关键.本题易出现的错误是直接将后两项合并化简,因此要特别注意运算的顺序不能乱.
20、计算得( )
A、x5 B、x5y
C、y5 D、xy5
考点:分式的乘除法。
分析:分式的运算首先要分清运算顺序,在这个题目中,首先进行乘方运算,然后统一成乘法运算,最后进行约分运算.
解答:解:原式=,
故选A.
点评:在计算过程中需要注意的是运算顺序.并且这类计算最终转化为约分运算.
二、填空题(共6小题)
21、已知M=,那么M,N的大小关系是 M>N .(填“>”或“<”)
考点:有理数大小比较;分式的乘除法。
专题:整体思想;换元法。
分析:先令21998=n,再运用作商法得出M÷N>1,从而得出M,N的大小关系.
解答:解:令21998=n,则21999=2 21998=2n,22000=4n,
∴M÷N=÷=.
∴M>N.
故答案为:M>N.
点评:本题考查了分数的大小比较,难度较大.本题采取换元作商法大大降低了计算量,且不容易出错.
22、(a2m+3am+2)÷(am+1)= am+2 .
考点:整式的除法;因式分解-十字相乘法等;分式的乘除法。
专题:计算题;整体思想;因式分解。
分析:题目是多项式除以多项式,可先将被除式中的多项式a2m+3am+2分解因式,再根据分式的除法法则进行计算.
解答:解:∵a2m+3am+2,
=(am)2+3(am)+2,
=(am+2)(am+1),
∴(a2m+3am+2)÷(am+1),
=,
=am+2.
故答案为:am+2.
点评:本题主要考查了运用十字相乘法分解因式a2m+3am+2及根据分式的基本性质进行分式的约分.多项式除以多项式的内容在初中教材大纲中不学习,本题属于竞赛题型,有一定难度.本题的关键是想到将被除式a2m+3am+2分解因式,难点是将am看作一个字母,则它是关于这个字母的二次三项式,因此可以运用十字相乘法分解因式.
23、多项式4x2+4x+1分解因式的结果是 (2x+1)2 ;计算的结果是
考点:因式分解-运用公式法;分式的乘除法。
分析:①用完全平方公式分解即可;
②把除法统一为乘法,再约分、化简即可.
解答:解:①4x2+4x+1=(2x+1)2;
②÷2xb=×=.
点评:整个式子为三项,有两项平方项,一项为平方项的底数的积的±2倍时,应考虑运用完全平方公式进行分解;分式的除法应统一为乘法后再进行计算.
24、,( )= xy2 ;
= ﹣ ;
考点:分式的基本性质;分式的乘除法。
分析:(1)根据分式的基本性质把的分母化为x2y的形式即可;
(2)找出分子、分母的公因式,把分子、分母同时除以其公因式即可.
解答:解:(1)∵把的分子、分母同时乘以xy得,==,
∴( )=xy2.
(2)∵分式中分子、分母的公因式为4abc3,
∴=﹣.
点评:本题考查的是分式的基本性质,即分式的分子、分母同时乘以或除以一个不为0的数,分式的值不变.
25、①分式与的最简公分母是 x(x+3)(x﹣3) ;
②分式的值为零的条件是 a=1且a≠﹣1 ;
③计算(xy﹣x2) = x2y .
考点:最简公分母;分式的值为零的条件;分式的乘除法。
分析:利用分式的混合运算法则计算即可.
解答:解:①两个分式的分母可分解为x(x﹣3),(x+3)(x﹣3),所以最简公分母是x(x+3)(x﹣3);
②此分式的值为0的条件是分子a﹣1=0,而分母b+1≠0,即a=1,b≠﹣1;
③(xy﹣x2) =﹣x(x﹣y) =x2y.
点评:①考查了确定最简公分母的方法;②考查了分式为0时的条件;③考查了简单的分式计算.
26、(2011 聊城)化简:÷= .
考点:分式的乘除法。
分析:首先分解每个因式的分子与分母,把除法转化成乘法,然后约分即可求解.
解答:解:原式= =.
故答案为:
点评:本题考查了分式的化简,正确对分子、分母分解因式是关键.
三、解答题(共2小题)
27、给定下面一列分式:,(其中x≠0)
(1)把任意一个分式除以前面一个分式,你发现了什么规律?
(2)根据你发现的规律,试写出给定的那列分式中的第7个分式.
考点:规律型:数字的变化类;分式的基本性质;分式的乘除法。
专题:规律型。
分析:(1)将任意一个分式除以前面一个分式,可得出规律.
(2)由(1)可知任意一个分式除以前面一个分式恒等于一个代数式,由此可得出第7个分式.
解答:解:(1)第二个分式除以第一个分式得﹣,第三个分式除以第二个分式得﹣,
同理,第四个分式除以第三个分式也是﹣,故规律是任意一个分式除以前面一个分式;
(2)由(1)可知该第7个分式应该是×=.
点评:本题涉及数字的变化及数列的相关知识,根据题干的规律能找到一般表达式,难度中等.
28、(1)已知恒等式x3﹣x2﹣x+1=(x﹣1)(x2+kx﹣1),求k的值;
(2)若x是整数,求证:是整数.
考点:多项式乘多项式;因式分解-运用公式法;分式的乘除法;解一元一次方程。
专题:计算题;方程思想。
分析:(1)先将等式右边展开计算,再根据多项式恒等的性质,两边对应项系数相等,列出关于k的方程,从而求出k的值;
(2)把(1)中k的值代入,可将x3﹣x2﹣x+1因式分解,再进行分式的除法运算,可求出的结果,然后根据条件x是整数,即可得证.
解答:解:(1)由题设知,(x﹣1)(x2+kx﹣1)=x3+(k﹣1)x2﹣(k+1)x+1,
所以x3﹣x2﹣x+1=x3+(k﹣1)x2﹣(k+1)x+1,
从而有k﹣1=﹣1,﹣k﹣1=﹣1,
解得k=0.
故所求k的值为0;
(2)由(1)知k=0,则x3﹣x2﹣x+1=(x﹣1)(x2﹣1)=(x﹣1)2(x+1),
∴==x+1.
又∵x是整数,
∴x+1是整数.
故是整数.
点评:本题主要考查了多项式乘多项式的法则,因式分解及分式的除法.由于多项式除以多项式的内容在初中教材大纲中不学习,故本题第二问有一定难度,属于竞赛题型.解决第一问的关键是根据多项式乘多项式的法则,利用两边对应项系数相等,列出关于k的方程;解决第二问的关键是利用(1)的结论,将多项式x3﹣x2﹣x+1因式分解.
