16.1约分的专题训练(附答案及解析)
文档属性
| 名称 | 16.1约分的专题训练(附答案及解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 200.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-22 19:04:13 | ||
图片预览
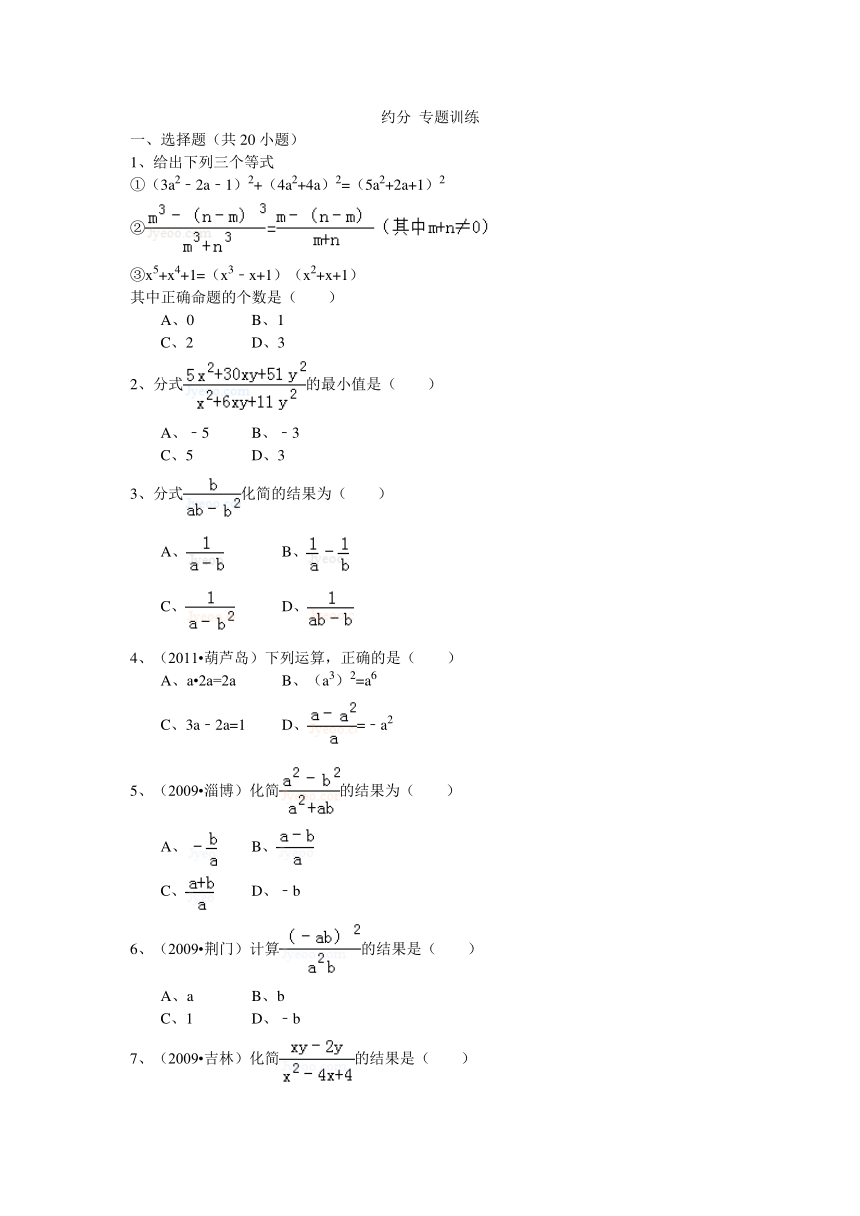




文档简介
约分 专题训练
一、选择题(共20小题)
1、给出下列三个等式
①(3a2﹣2a﹣1)2+(4a2+4a)2=(5a2+2a+1)2
②
③x5+x4+1=(x3﹣x+1)(x2+x+1)
其中正确命题的个数是( )
A、0 B、1
C、2 D、3
2、分式的最小值是( )
A、﹣5 B、﹣3
C、5 D、3
3、分式化简的结果为( )
A、 B、
C、 D、
4、(2011 葫芦岛)下列运算,正确的是( )
A、a 2a=2a B、(a3)2=a6
C、3a﹣2a=1 D、=﹣a2
5、(2009 淄博)化简的结果为( )
A、 B、
C、 D、﹣b
6、(2009 荆门)计算的结果是( )
A、a B、b
C、1 D、﹣b
7、(2009 吉林)化简的结果是( )
A、 B、
C、 D、
8、(2008 无锡)计算的结果为( )
A、b B、a
C、1 D、
9、(2008 太原)化简的结果是( )
A、 B、
C、 D、
10、(2007 无锡)化简分式的结果为( )
A、 B、
C、 D、
11、(2003 河北)化简的结果是( )
A、 B、
C、 D、
12、(2001 湖州)化简的结果为( )
A、x+y B、x﹣y
C、y﹣x D、﹣x﹣y
13、下列约分正确的是( )
A、 B、=0
C、= D、
14、下列约分正确的是( )
A、 B、
C、 D、
15、下面化简正确的是( )
A、=0 B、=﹣1
C、=2 D、=x+y
16、下列约分正确的是( )
A、=0 B、
C、 D、
17、化简:的结果是( )
A、 B、
C、﹣ D、﹣
18、分式化简的结果是( )
A、 B、
C、 D、
19、下列约分中正确的是( )
A、 B、
C、 D、
20、下列运算正确的是( )
A、 B、
C、 D、
二、填空题(共4小题)
21、已知x为整数,且分式的值为整数,则x= _________ .
22、(2011 盐城)化简= _________ .
23、(2010 中山)化简:= _________ .
24、(2010 丽江)化简分式的结果是 _________ .
三、解答题(共6小题)
25、先化简,再求值(3x4﹣2x3)÷(﹣x)﹣(x﹣x2) 3x,其中.
26、(2007 广州)请以下列三个代数式中任选两个构造一个分式,并化简该分式.
a2﹣1;ab﹣b;b+ab.
27、(2005 广州)计算:
28、约分(1);
(2).
29、
30、约分:
答案与评分标准
一、选择题(共20小题)
1、给出下列三个等式
①(3a2﹣2a﹣1)2+(4a2+4a)2=(5a2+2a+1)2
②
③x5+x4+1=(x3﹣x+1)(x2+x+1)
其中正确命题的个数是( )
A、0 B、1
C、2 D、3
考点:多项式乘多项式;约分。
分析:本题根据多项式乘多项式的定义分别进行计算,再进行约分,即可求出答案.
解答:解:①(3a2﹣2a﹣1)2+(4a2+4a)2=(3a2﹣2a﹣1+4a2+4a)2﹣2(3a2﹣2a﹣1)(4a2+4a)
=(7a2+2a﹣1)2﹣2(3a2﹣2a﹣1)(4a2+4a)
故本选项错误;
故本选项错误;
③x5+x4+1不等于(x3﹣x+1)(x2+x+1),故本选项错误;
故选A.
点评:本题主要考查了多项式乘多项式,解题的关键是先进行化简,再进行约分.
2、分式的最小值是( )
A、﹣5 B、﹣3
C、5 D、3
考点:完全平方式;约分。
专题:计算题。
分析:把分子先整理成分母的倍数加上4y2的形式,然后约分并整理成分子是常数的形式,分母再利用配方法配方,然后根据二次函数的最值问题进行解答.
解答:解:,
=,
=5﹣,
=5﹣,
当=﹣3时,原式取最小值,最小值为5﹣=3.
故答案为:3.
点评:本题考查了完全平方式与约分,把原式进行整理是解题的关键,本题难度较大,整理时要仔细小心.
3、分式化简的结果为( )
A、 B、
C、 D、
考点:分式的基本性质;因式分解-提公因式法;约分。
专题:计算题。
分析:首先把分式的分母分解因式成b(a﹣b),再利用分式的基本性质约分即可.
解答:解:,
=,
=.
故选A.
点评:本题主要考查了分式的基本性质,用提公因式法分解因式,约分等知识点,解此题的关键是正确分解因式.
4、(2011 葫芦岛)下列运算,正确的是( )
A、a 2a=2a B、(a3)2=a6
C、3a﹣2a=1 D、=﹣a2
考点:约分;合并同类项;幂的乘方与积的乘方;单项式乘单项式。
分析:根据同底数幂的乘法、幂的乘方,分式的约分分别进行计算即可得出正确答案.
解答:解:A、a 2a=2a2,故本选项错误;
B、(a3)2=a6,故本选项正确;
C、3a﹣2a=a,故本选项错误;
D、=1﹣a,故本选项错误.
故选B.
点评:本题主要考查了同底数幂的乘法、幂的运算,分式的约分,在进行计算时要注意结果的符号和指数的变化.
5、(2009 淄博)化简的结果为( )
A、 B、
C、 D、﹣b
考点:约分。
分析:把分式进行化简就是对分式进行约分,首先要对分子、分母进行分解因式,把互为相反数的因式化为相同的因式.
解答:解:=.
故选B.
点评:正确的分解因式是分式化简的关键.
6、(2009 荆门)计算的结果是( )
A、a B、b
C、1 D、﹣b
考点:约分。
分析:因为负数的平方也是正数,所以分子(﹣ab)2=ab ab,分母a2b=a ab,约分即可.
解答:解:=,
故选B.
点评:分子和分母同乘以(或除以)一个不为0的数,分数值不变.
7、(2009 吉林)化简的结果是( )
A、 B、
C、 D、
考点:约分。
分析:首先将分子、分母进行因式分解,然后根据分式的基本性质约分.
解答:解:==,
故选D.
点评:本题考查因式分解及分式的约分,因式分解是约分的基础.
8、(2008 无锡)计算的结果为( )
A、b B、a
C、1 D、
考点:约分。
分析:将分式分子先去括号,再约分,即可求解.
解答:解:==a,故选B.
点评:本题考查幂的运算,涉及到积的乘方,分式的约分,按运算顺序,先做积的乘方,再约分.
9、(2008 太原)化简的结果是( )
A、 B、
C、 D、
考点:约分。
分析:首先把分子、分母分别分解因式,再根据分式的基本性质进行约分、化简即可.
解答:解:==,
故选B.
点评:解答此类题一定要熟练掌握因式分解与分式的基本性质.
10、(2007 无锡)化简分式的结果为( )
A、 B、
C、 D、
考点:约分。
分析:最简分式的标准是分子,分母中不含有公因式,不能再约分.判断的方法是把分子、分母分解因式,并且观察有无互为相反数的因式,这样的因式可以通过符号变化化为相同的因式从而进行约分.
解答:解:原式=.
故选A.
点评:分式的化简过程,首先要把分子分母分解因式,互为相反数的因式是比较易忽视的问题.在解题中一定要引起注意.
11、(2003 河北)化简的结果是( )
A、 B、
C、 D、
考点:约分。
分析:首先把分式分子分母因式分解,然后把相同的因子约掉.
解答:解:=,
=﹣,
故选B.
点评:解答本题主要把分式分子分母进行因式分解,然后进行约分.
12、(2001 湖州)化简的结果为( )
A、x+y B、x﹣y
C、y﹣x D、﹣x﹣y
考点:约分。
分析:根据分式的基本性质,把分子分解因式再与分母约分即可.
解答:解:根据分式的基本性质可知==x+y.
故选A.
点评:化简分式一定要根据分式的基本性质,无论是把分式的分子和分母扩大还是缩小相同的倍数,分式的值不变.
13、下列约分正确的是( )
A、 B、=0
C、= D、
考点:约分。
分析:不改变分式的值就是依据分式的基本性质进行变化,分子分母上同时乘以或除以同一个非0的数或式子,分式的值不变.因而变化时,分子分母上同时乘以或除以的式子必须是同一个式子且非0.
解答:解:A、,故A错误;
B、,故B错误;
C、==,故C正确;
D、,故D错误.
故选C.
点评:在分式约分中,必须严格按照分式的基本性质进行.
14、下列约分正确的是( )
A、 B、
C、 D、
考点:约分。
分析:根据分式的基本性质作答.
解答:解:A、,错误;
B、,错误;
C、,正确;
D、,错误.
故选C.
点评:本题主要考查了分式的性质,注意约分是约去分子、分母的公因式,并且分子与分母相同时约分结果应是1,而不是0.
15、下面化简正确的是( )
A、=0 B、=﹣1
C、=2 D、=x+y
考点:约分。
分析:分式的基本性质是分式的分子、分母同时乘以或除以同一个非0的数或式子,分式的值不变.据此作答.
解答:解:A、分子分母中同时除以2a+1,分子、分母都变成1,故式子的值是1.错误;
B、(a﹣b)2=(b﹣a)2,因而分式的值是1.错误;
C、分子、分母同时除以﹣x+3,正确;
D、x2+y2≠(x+y)2,错误.
故选C
点评:解答此类题一定要熟练掌握分式的基本性质.
16、下列约分正确的是( )
A、=0 B、
C、 D、
考点:约分。
分析:分子和分母同乘以(或除以)一个不为0的数,分数值不变.
解答:解:A、=1,错误;
B、=,正确;
C、,错误;
D、分式的分子、分母同时加上一个不为0数,分式的值要改变,错误.
故选B.
点评:根据分式的基本性质,无论是把分式的分子和分母扩大还是缩小相同的倍数,分式的值不变.
17、化简:的结果是( )
A、 B、
C、﹣ D、﹣
考点:约分。
分析:对分式进行化简时,若分式分子分母是多项式时,应先进行因式分解,然后再约分.
解答:解:=.
故选C.
点评:进行分式的化简运算时,对于能分解因式的多项式应先分解因式,再进行约分,并注意体会y﹣x=﹣(x﹣y).
18、分式化简的结果是( )
A、 B、
C、 D、
考点:约分。
分析:首先把分式的分子和分母分解因式,然后进行约分.
解答:解:==﹣,故选答案C.
点评:解答此类题一定要熟练掌握分式的基本性质.分式的基本性质:分式的分子和分母同时乘以(或除以)同一个不为0的整式,分式的值不变.
19、下列约分中正确的是( )
A、 B、
C、 D、
考点:约分。
分析:根据分式的基本性质对各式进行约分即可.
解答:解:A、错误,==a+b;
B、错误,分子、分母没有公因式不能约分;
C、正确;
D、错误,分子、分母没有公因式不能约分.
故选C.
点评:本题考查的是分式的约分,即当分式的分子、分母有公因式时,应根据分式的基本性质约去公因式.
20、下列运算正确的是( )
A、 B、
C、 D、
考点:约分。
分析:先将分式的分子与分母,能分解因式的进行因式分解,然后进行约分,化出最后的结果.
解答:解:A、不能再计算,故A错误;
B、=﹣=﹣1,故B正确;
C、,故C错误;
D、==a+b,故D错误;
故选B.
点评:如果分子与分母是多项式,一定先进行因式分解.
二、填空题(共4小题)
21、已知x为整数,且分式的值为整数,则x= 0或2或3 .
考点:分式的值;约分。
分析:首先化简分式,得=.要使它的值为整数,则x﹣1应是2的约数,即x﹣1=±1或±2,同时注意原分式有意义的条件:x≠±1.
解答:解:∵=,
∴根据题意,得
x﹣1=±1或±2,
则x=2或0或3或﹣1.
又x≠±1,
则x=0或2或3.
点评:此类题首先要正确化简分式,然后要保证分式的值为整数,则根据分母应是分子的约数,进行分析.
注意:字母的值必须保证使原分式有意义.
22、(2011 盐城)化简= x+3 .
考点:约分。
分析:分式的基本性质是分式的分子、分母同时乘以或除以同一个非0的数或式子,分式的值不变.据此化简.
解答:解:==x+3.
点评:分式的化简中,若分子、分母中是多项式时,要把多项式先分解因式,再约分.
23、(2010 中山)化简:= x﹣y+1 .
考点:约分。
分析:观察分子可发现x2﹣2xy+y2正好是完全平方式,然后再用平方差公式进行因式分解即可.
解答:解:原式===x﹣y+1.
点评:在完成此类化简题时,应先将分子、分母中能够分解因式的部分进行分解因式.有些需要先提取公因式,而有些则需要运用公式法进行分解因式.通过分解因式,把分子分母中能够分解因式的部分,分解成乘积的形式,然后找到其中的公因式约去.
24、(2010 丽江)化简分式的结果是 .
考点:约分。
分析:将分子、分母因式分解并进行约分.
解答:解:原式=.
点评:解答此类题一定要熟练掌握分式的基本性质:分式的分子和分母都乘以或都除以同一个不为0的数或整式,分式的值不变.
三、解答题(共6小题)
25、先化简,再求值(3x4﹣2x3)÷(﹣x)﹣(x﹣x2) 3x,其中.
考点:整式的混合运算—化简求值;约分。
专题:计算题。
分析:对(3x4﹣2x3)÷(﹣x)﹣(x﹣x2) 3x中的(3x4﹣2x3)÷(﹣x)部分利用乘法的结合律3x4×()﹣2x3×()得﹣3x3+2x2;对(x﹣x2) 3x部分仍然利用乘法的结合律(x×3x﹣x2×3x)得(3x2﹣3x3).再去括号得﹣3x3+2x2﹣3x2+3x3=﹣x2,将代入上面化简后的式子即可.
解答:解:
原式=﹣3x3+2x2﹣(3x2﹣3x3)
=﹣3x3+2x2﹣3x2+3x3
=﹣x2
当时,原式==
点评:本题主要考查学生对乘法结合律分式与分式约分的运用,熟记并灵活运用是解题的关键.
26、(2007 广州)请以下列三个代数式中任选两个构造一个分式,并化简该分式.
a2﹣1;ab﹣b;b+ab.
考点:约分;分式的定义。
专题:开放型。
分析:要构造分式,可令其中一个式子做分母,另外一个做分子即可.然后将分子和分母分别进行因式分解或提取公因式,然后再进行约分、化简就能得出所求的结果.
解答:解:本题共有六种答案,只要给出其中一种答案,均正确.
;
;
;
;
.
点评:在完成此类化简题时,应先将分子、分母中能够分解因式的部分进行分解因式.有些需要先提取公因式,而有些则需要运用公式法进行分解因式.通过分解因式,把分子分母中能够分解因式的部分,分解成乘积的形式,然后找到其中的公因式约去.
27、(2005 广州)计算:
考点:约分。
分析:首先给分子、分母分解因式,然后进行约分.
解答:解:.
点评:解答此类题一定要熟练掌握分式的基本性质.
28、约分(1);
(2).
考点:约分。
分析:根据分式的基本性质:分式的分子和分母同时乘以(或除以)同一个不为0的整式,分式的值不变作答.
解答:解:(1);
(2).
点评:解答此类题一定要熟练掌握分式的基本性质.
29、
考点:约分。
分析:首先给分子、分母进行分解因式,然后进行约分.
解答:解:==.
点评:解答此类题一定要熟练掌握分式的基本性质.
30、约分:
考点:约分。
分析:先把分子分解因式,然后找出分子、分母的公因式,再根据分式的基本性质,分子、分母都除以公因式即可.
解答:解:==.
点评:把分式的分子分解因式,然后找出分子、分母的公因式是约分的关键.
一、选择题(共20小题)
1、给出下列三个等式
①(3a2﹣2a﹣1)2+(4a2+4a)2=(5a2+2a+1)2
②
③x5+x4+1=(x3﹣x+1)(x2+x+1)
其中正确命题的个数是( )
A、0 B、1
C、2 D、3
2、分式的最小值是( )
A、﹣5 B、﹣3
C、5 D、3
3、分式化简的结果为( )
A、 B、
C、 D、
4、(2011 葫芦岛)下列运算,正确的是( )
A、a 2a=2a B、(a3)2=a6
C、3a﹣2a=1 D、=﹣a2
5、(2009 淄博)化简的结果为( )
A、 B、
C、 D、﹣b
6、(2009 荆门)计算的结果是( )
A、a B、b
C、1 D、﹣b
7、(2009 吉林)化简的结果是( )
A、 B、
C、 D、
8、(2008 无锡)计算的结果为( )
A、b B、a
C、1 D、
9、(2008 太原)化简的结果是( )
A、 B、
C、 D、
10、(2007 无锡)化简分式的结果为( )
A、 B、
C、 D、
11、(2003 河北)化简的结果是( )
A、 B、
C、 D、
12、(2001 湖州)化简的结果为( )
A、x+y B、x﹣y
C、y﹣x D、﹣x﹣y
13、下列约分正确的是( )
A、 B、=0
C、= D、
14、下列约分正确的是( )
A、 B、
C、 D、
15、下面化简正确的是( )
A、=0 B、=﹣1
C、=2 D、=x+y
16、下列约分正确的是( )
A、=0 B、
C、 D、
17、化简:的结果是( )
A、 B、
C、﹣ D、﹣
18、分式化简的结果是( )
A、 B、
C、 D、
19、下列约分中正确的是( )
A、 B、
C、 D、
20、下列运算正确的是( )
A、 B、
C、 D、
二、填空题(共4小题)
21、已知x为整数,且分式的值为整数,则x= _________ .
22、(2011 盐城)化简= _________ .
23、(2010 中山)化简:= _________ .
24、(2010 丽江)化简分式的结果是 _________ .
三、解答题(共6小题)
25、先化简,再求值(3x4﹣2x3)÷(﹣x)﹣(x﹣x2) 3x,其中.
26、(2007 广州)请以下列三个代数式中任选两个构造一个分式,并化简该分式.
a2﹣1;ab﹣b;b+ab.
27、(2005 广州)计算:
28、约分(1);
(2).
29、
30、约分:
答案与评分标准
一、选择题(共20小题)
1、给出下列三个等式
①(3a2﹣2a﹣1)2+(4a2+4a)2=(5a2+2a+1)2
②
③x5+x4+1=(x3﹣x+1)(x2+x+1)
其中正确命题的个数是( )
A、0 B、1
C、2 D、3
考点:多项式乘多项式;约分。
分析:本题根据多项式乘多项式的定义分别进行计算,再进行约分,即可求出答案.
解答:解:①(3a2﹣2a﹣1)2+(4a2+4a)2=(3a2﹣2a﹣1+4a2+4a)2﹣2(3a2﹣2a﹣1)(4a2+4a)
=(7a2+2a﹣1)2﹣2(3a2﹣2a﹣1)(4a2+4a)
故本选项错误;
故本选项错误;
③x5+x4+1不等于(x3﹣x+1)(x2+x+1),故本选项错误;
故选A.
点评:本题主要考查了多项式乘多项式,解题的关键是先进行化简,再进行约分.
2、分式的最小值是( )
A、﹣5 B、﹣3
C、5 D、3
考点:完全平方式;约分。
专题:计算题。
分析:把分子先整理成分母的倍数加上4y2的形式,然后约分并整理成分子是常数的形式,分母再利用配方法配方,然后根据二次函数的最值问题进行解答.
解答:解:,
=,
=5﹣,
=5﹣,
当=﹣3时,原式取最小值,最小值为5﹣=3.
故答案为:3.
点评:本题考查了完全平方式与约分,把原式进行整理是解题的关键,本题难度较大,整理时要仔细小心.
3、分式化简的结果为( )
A、 B、
C、 D、
考点:分式的基本性质;因式分解-提公因式法;约分。
专题:计算题。
分析:首先把分式的分母分解因式成b(a﹣b),再利用分式的基本性质约分即可.
解答:解:,
=,
=.
故选A.
点评:本题主要考查了分式的基本性质,用提公因式法分解因式,约分等知识点,解此题的关键是正确分解因式.
4、(2011 葫芦岛)下列运算,正确的是( )
A、a 2a=2a B、(a3)2=a6
C、3a﹣2a=1 D、=﹣a2
考点:约分;合并同类项;幂的乘方与积的乘方;单项式乘单项式。
分析:根据同底数幂的乘法、幂的乘方,分式的约分分别进行计算即可得出正确答案.
解答:解:A、a 2a=2a2,故本选项错误;
B、(a3)2=a6,故本选项正确;
C、3a﹣2a=a,故本选项错误;
D、=1﹣a,故本选项错误.
故选B.
点评:本题主要考查了同底数幂的乘法、幂的运算,分式的约分,在进行计算时要注意结果的符号和指数的变化.
5、(2009 淄博)化简的结果为( )
A、 B、
C、 D、﹣b
考点:约分。
分析:把分式进行化简就是对分式进行约分,首先要对分子、分母进行分解因式,把互为相反数的因式化为相同的因式.
解答:解:=.
故选B.
点评:正确的分解因式是分式化简的关键.
6、(2009 荆门)计算的结果是( )
A、a B、b
C、1 D、﹣b
考点:约分。
分析:因为负数的平方也是正数,所以分子(﹣ab)2=ab ab,分母a2b=a ab,约分即可.
解答:解:=,
故选B.
点评:分子和分母同乘以(或除以)一个不为0的数,分数值不变.
7、(2009 吉林)化简的结果是( )
A、 B、
C、 D、
考点:约分。
分析:首先将分子、分母进行因式分解,然后根据分式的基本性质约分.
解答:解:==,
故选D.
点评:本题考查因式分解及分式的约分,因式分解是约分的基础.
8、(2008 无锡)计算的结果为( )
A、b B、a
C、1 D、
考点:约分。
分析:将分式分子先去括号,再约分,即可求解.
解答:解:==a,故选B.
点评:本题考查幂的运算,涉及到积的乘方,分式的约分,按运算顺序,先做积的乘方,再约分.
9、(2008 太原)化简的结果是( )
A、 B、
C、 D、
考点:约分。
分析:首先把分子、分母分别分解因式,再根据分式的基本性质进行约分、化简即可.
解答:解:==,
故选B.
点评:解答此类题一定要熟练掌握因式分解与分式的基本性质.
10、(2007 无锡)化简分式的结果为( )
A、 B、
C、 D、
考点:约分。
分析:最简分式的标准是分子,分母中不含有公因式,不能再约分.判断的方法是把分子、分母分解因式,并且观察有无互为相反数的因式,这样的因式可以通过符号变化化为相同的因式从而进行约分.
解答:解:原式=.
故选A.
点评:分式的化简过程,首先要把分子分母分解因式,互为相反数的因式是比较易忽视的问题.在解题中一定要引起注意.
11、(2003 河北)化简的结果是( )
A、 B、
C、 D、
考点:约分。
分析:首先把分式分子分母因式分解,然后把相同的因子约掉.
解答:解:=,
=﹣,
故选B.
点评:解答本题主要把分式分子分母进行因式分解,然后进行约分.
12、(2001 湖州)化简的结果为( )
A、x+y B、x﹣y
C、y﹣x D、﹣x﹣y
考点:约分。
分析:根据分式的基本性质,把分子分解因式再与分母约分即可.
解答:解:根据分式的基本性质可知==x+y.
故选A.
点评:化简分式一定要根据分式的基本性质,无论是把分式的分子和分母扩大还是缩小相同的倍数,分式的值不变.
13、下列约分正确的是( )
A、 B、=0
C、= D、
考点:约分。
分析:不改变分式的值就是依据分式的基本性质进行变化,分子分母上同时乘以或除以同一个非0的数或式子,分式的值不变.因而变化时,分子分母上同时乘以或除以的式子必须是同一个式子且非0.
解答:解:A、,故A错误;
B、,故B错误;
C、==,故C正确;
D、,故D错误.
故选C.
点评:在分式约分中,必须严格按照分式的基本性质进行.
14、下列约分正确的是( )
A、 B、
C、 D、
考点:约分。
分析:根据分式的基本性质作答.
解答:解:A、,错误;
B、,错误;
C、,正确;
D、,错误.
故选C.
点评:本题主要考查了分式的性质,注意约分是约去分子、分母的公因式,并且分子与分母相同时约分结果应是1,而不是0.
15、下面化简正确的是( )
A、=0 B、=﹣1
C、=2 D、=x+y
考点:约分。
分析:分式的基本性质是分式的分子、分母同时乘以或除以同一个非0的数或式子,分式的值不变.据此作答.
解答:解:A、分子分母中同时除以2a+1,分子、分母都变成1,故式子的值是1.错误;
B、(a﹣b)2=(b﹣a)2,因而分式的值是1.错误;
C、分子、分母同时除以﹣x+3,正确;
D、x2+y2≠(x+y)2,错误.
故选C
点评:解答此类题一定要熟练掌握分式的基本性质.
16、下列约分正确的是( )
A、=0 B、
C、 D、
考点:约分。
分析:分子和分母同乘以(或除以)一个不为0的数,分数值不变.
解答:解:A、=1,错误;
B、=,正确;
C、,错误;
D、分式的分子、分母同时加上一个不为0数,分式的值要改变,错误.
故选B.
点评:根据分式的基本性质,无论是把分式的分子和分母扩大还是缩小相同的倍数,分式的值不变.
17、化简:的结果是( )
A、 B、
C、﹣ D、﹣
考点:约分。
分析:对分式进行化简时,若分式分子分母是多项式时,应先进行因式分解,然后再约分.
解答:解:=.
故选C.
点评:进行分式的化简运算时,对于能分解因式的多项式应先分解因式,再进行约分,并注意体会y﹣x=﹣(x﹣y).
18、分式化简的结果是( )
A、 B、
C、 D、
考点:约分。
分析:首先把分式的分子和分母分解因式,然后进行约分.
解答:解:==﹣,故选答案C.
点评:解答此类题一定要熟练掌握分式的基本性质.分式的基本性质:分式的分子和分母同时乘以(或除以)同一个不为0的整式,分式的值不变.
19、下列约分中正确的是( )
A、 B、
C、 D、
考点:约分。
分析:根据分式的基本性质对各式进行约分即可.
解答:解:A、错误,==a+b;
B、错误,分子、分母没有公因式不能约分;
C、正确;
D、错误,分子、分母没有公因式不能约分.
故选C.
点评:本题考查的是分式的约分,即当分式的分子、分母有公因式时,应根据分式的基本性质约去公因式.
20、下列运算正确的是( )
A、 B、
C、 D、
考点:约分。
分析:先将分式的分子与分母,能分解因式的进行因式分解,然后进行约分,化出最后的结果.
解答:解:A、不能再计算,故A错误;
B、=﹣=﹣1,故B正确;
C、,故C错误;
D、==a+b,故D错误;
故选B.
点评:如果分子与分母是多项式,一定先进行因式分解.
二、填空题(共4小题)
21、已知x为整数,且分式的值为整数,则x= 0或2或3 .
考点:分式的值;约分。
分析:首先化简分式,得=.要使它的值为整数,则x﹣1应是2的约数,即x﹣1=±1或±2,同时注意原分式有意义的条件:x≠±1.
解答:解:∵=,
∴根据题意,得
x﹣1=±1或±2,
则x=2或0或3或﹣1.
又x≠±1,
则x=0或2或3.
点评:此类题首先要正确化简分式,然后要保证分式的值为整数,则根据分母应是分子的约数,进行分析.
注意:字母的值必须保证使原分式有意义.
22、(2011 盐城)化简= x+3 .
考点:约分。
分析:分式的基本性质是分式的分子、分母同时乘以或除以同一个非0的数或式子,分式的值不变.据此化简.
解答:解:==x+3.
点评:分式的化简中,若分子、分母中是多项式时,要把多项式先分解因式,再约分.
23、(2010 中山)化简:= x﹣y+1 .
考点:约分。
分析:观察分子可发现x2﹣2xy+y2正好是完全平方式,然后再用平方差公式进行因式分解即可.
解答:解:原式===x﹣y+1.
点评:在完成此类化简题时,应先将分子、分母中能够分解因式的部分进行分解因式.有些需要先提取公因式,而有些则需要运用公式法进行分解因式.通过分解因式,把分子分母中能够分解因式的部分,分解成乘积的形式,然后找到其中的公因式约去.
24、(2010 丽江)化简分式的结果是 .
考点:约分。
分析:将分子、分母因式分解并进行约分.
解答:解:原式=.
点评:解答此类题一定要熟练掌握分式的基本性质:分式的分子和分母都乘以或都除以同一个不为0的数或整式,分式的值不变.
三、解答题(共6小题)
25、先化简,再求值(3x4﹣2x3)÷(﹣x)﹣(x﹣x2) 3x,其中.
考点:整式的混合运算—化简求值;约分。
专题:计算题。
分析:对(3x4﹣2x3)÷(﹣x)﹣(x﹣x2) 3x中的(3x4﹣2x3)÷(﹣x)部分利用乘法的结合律3x4×()﹣2x3×()得﹣3x3+2x2;对(x﹣x2) 3x部分仍然利用乘法的结合律(x×3x﹣x2×3x)得(3x2﹣3x3).再去括号得﹣3x3+2x2﹣3x2+3x3=﹣x2,将代入上面化简后的式子即可.
解答:解:
原式=﹣3x3+2x2﹣(3x2﹣3x3)
=﹣3x3+2x2﹣3x2+3x3
=﹣x2
当时,原式==
点评:本题主要考查学生对乘法结合律分式与分式约分的运用,熟记并灵活运用是解题的关键.
26、(2007 广州)请以下列三个代数式中任选两个构造一个分式,并化简该分式.
a2﹣1;ab﹣b;b+ab.
考点:约分;分式的定义。
专题:开放型。
分析:要构造分式,可令其中一个式子做分母,另外一个做分子即可.然后将分子和分母分别进行因式分解或提取公因式,然后再进行约分、化简就能得出所求的结果.
解答:解:本题共有六种答案,只要给出其中一种答案,均正确.
;
;
;
;
.
点评:在完成此类化简题时,应先将分子、分母中能够分解因式的部分进行分解因式.有些需要先提取公因式,而有些则需要运用公式法进行分解因式.通过分解因式,把分子分母中能够分解因式的部分,分解成乘积的形式,然后找到其中的公因式约去.
27、(2005 广州)计算:
考点:约分。
分析:首先给分子、分母分解因式,然后进行约分.
解答:解:.
点评:解答此类题一定要熟练掌握分式的基本性质.
28、约分(1);
(2).
考点:约分。
分析:根据分式的基本性质:分式的分子和分母同时乘以(或除以)同一个不为0的整式,分式的值不变作答.
解答:解:(1);
(2).
点评:解答此类题一定要熟练掌握分式的基本性质.
29、
考点:约分。
分析:首先给分子、分母进行分解因式,然后进行约分.
解答:解:==.
点评:解答此类题一定要熟练掌握分式的基本性质.
30、约分:
考点:约分。
分析:先把分子分解因式,然后找出分子、分母的公因式,再根据分式的基本性质,分子、分母都除以公因式即可.
解答:解:==.
点评:把分式的分子分解因式,然后找出分子、分母的公因式是约分的关键.
