函数的单调性与最值 课件(共20张PPT)
文档属性
| 名称 | 函数的单调性与最值 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 796.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-17 11:39:20 | ||
图片预览








文档简介
(共20张PPT)
函数的单调性与最值
【学习目标】
01
理解函数的单调性、最大值、最小值及其几何意义;
02
会运用函数图象理解和研究函数的单调性,并利用单调性求最值或者求参数范围;
03
培养抽象概括、逻辑推理、运算求解等能力.
复习回顾
1.函数的单调性
(1)单调函数的定义
增函数 减函数
定义 一般地,设函数f(x)的定义域为I,区间D I,如果 x1,x2∈D 当x1f(x1)f(x1)>f(x2)
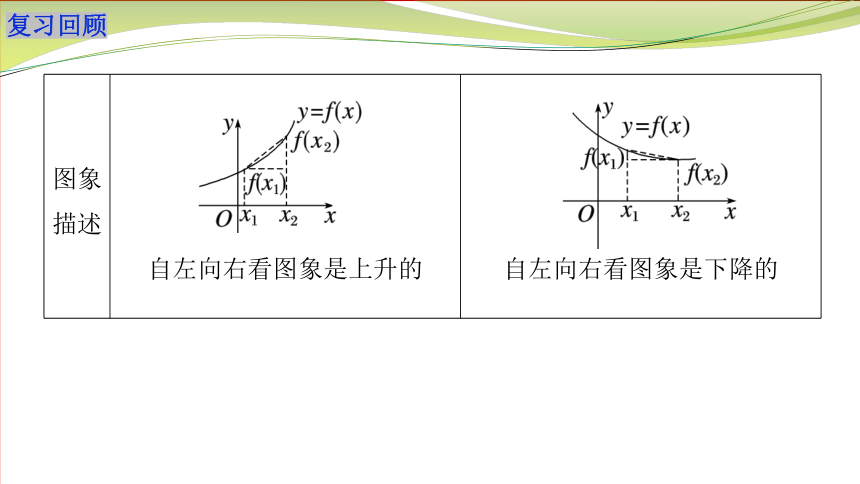
图象描述 自左向右看图象是上升的
自左向右看图象是下降的
复习回顾
(2)单调区间的定义
如果函数y=f(x)在区间D上_________或_________,那么就说函数y=f(x)在这一区间具有(严格的)单调性,区间D叫做y=f(x)的单调区间.
单调递增
单调递减
复习回顾
2.函数的最值
前提 设函数y=f(x)的定义域为I,如果存在实数M满足 条件 (1) x∈I, 都有________; (2) x0∈I, 使得_________ (1) x∈I,
都有_________;
(2) x0∈I,
使得_________
结论 M为最大值 M为最小值
f(x)≤M
f(x0)=M
f(x)≥M
f(x0)=M
复习回顾
专题一:判断、证明函数的单调性
D
B
专题一:判断、证明函数的单调性
D
(-1,0),(1,+∞)
(-∞,1),(2,+∞)
专题一:判断、证明函数的单调性
专题一:判断、证明函数的单调性
小结: 确定函数单调性的四种方法
(1)定义法;(2)导数法;(3)图象法;(4)性质法.
注意:证明的方法只有定义法和导数法.
专题二:函数单调性的应用
小结:利用单调性求参数的取值(范围).根据其单调性直接构建参数满足的方程(组)
(不等式(组))或先得到其图象的升降,再结合图象求解.
D
(-∞,1]
专题二:函数单调性的应用
(0,1)
小结:求解函数不等式,由条件脱去“f”,转化为自变量间的大小关系,应注意函数的定义域.
专题二:函数单调性的应用
B
专题二:函数单调性的应用
小结:比较函数值的大小时,转化到同一个单调区间内,然后利用函数的单调性解决.
A
专题三:求函数的最值
8
9
3
专题三:求函数的最值
求函数最值的三种基本方法:
单调性法:先确定函数的单调性,再由单调性求最值.
图象法:先作出函数的图象,再观察其最高点、最低点,求出最值.
对于较复杂函数,可用换元法化归为简单函数、或者运用导数,求出在给定区间上的极值,最后结合端点值,求出最值.
单调性
定 义
图象特征
应 用
判断方法
求最值
求参数范围
解不等式
定义法
图象变换
求导法
课堂小结
祝同学们前程似锦!
函数的单调性与最值
【学习目标】
01
理解函数的单调性、最大值、最小值及其几何意义;
02
会运用函数图象理解和研究函数的单调性,并利用单调性求最值或者求参数范围;
03
培养抽象概括、逻辑推理、运算求解等能力.
复习回顾
1.函数的单调性
(1)单调函数的定义
增函数 减函数
定义 一般地,设函数f(x)的定义域为I,区间D I,如果 x1,x2∈D 当x1
图象描述 自左向右看图象是上升的
自左向右看图象是下降的
复习回顾
(2)单调区间的定义
如果函数y=f(x)在区间D上_________或_________,那么就说函数y=f(x)在这一区间具有(严格的)单调性,区间D叫做y=f(x)的单调区间.
单调递增
单调递减
复习回顾
2.函数的最值
前提 设函数y=f(x)的定义域为I,如果存在实数M满足 条件 (1) x∈I, 都有________; (2) x0∈I, 使得_________ (1) x∈I,
都有_________;
(2) x0∈I,
使得_________
结论 M为最大值 M为最小值
f(x)≤M
f(x0)=M
f(x)≥M
f(x0)=M
复习回顾
专题一:判断、证明函数的单调性
D
B
专题一:判断、证明函数的单调性
D
(-1,0),(1,+∞)
(-∞,1),(2,+∞)
专题一:判断、证明函数的单调性
专题一:判断、证明函数的单调性
小结: 确定函数单调性的四种方法
(1)定义法;(2)导数法;(3)图象法;(4)性质法.
注意:证明的方法只有定义法和导数法.
专题二:函数单调性的应用
小结:利用单调性求参数的取值(范围).根据其单调性直接构建参数满足的方程(组)
(不等式(组))或先得到其图象的升降,再结合图象求解.
D
(-∞,1]
专题二:函数单调性的应用
(0,1)
小结:求解函数不等式,由条件脱去“f”,转化为自变量间的大小关系,应注意函数的定义域.
专题二:函数单调性的应用
B
专题二:函数单调性的应用
小结:比较函数值的大小时,转化到同一个单调区间内,然后利用函数的单调性解决.
A
专题三:求函数的最值
8
9
3
专题三:求函数的最值
求函数最值的三种基本方法:
单调性法:先确定函数的单调性,再由单调性求最值.
图象法:先作出函数的图象,再观察其最高点、最低点,求出最值.
对于较复杂函数,可用换元法化归为简单函数、或者运用导数,求出在给定区间上的极值,最后结合端点值,求出最值.
单调性
定 义
图象特征
应 用
判断方法
求最值
求参数范围
解不等式
定义法
图象变换
求导法
课堂小结
祝同学们前程似锦!
