北京课改版数学八年级上册同步课时练习:12.5角边角公理(第1课时)(Word版 含答案)
文档属性
| 名称 | 北京课改版数学八年级上册同步课时练习:12.5角边角公理(第1课时)(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 170.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-17 00:00:00 | ||
图片预览

文档简介
12.5 第1课时 角边角公理
有两角和它们的夹边分别相等的两个三角形全等(简记为:角边角或ASA).
1.下列条件中,不能判定△ABC≌△DEF的是( )
A.∠A=∠D,∠C =∠F,AC=DF
B.∠A=∠D,∠B =∠E,AB=DE
C.∠A=∠B,∠D =∠E,AD=BE
D.∠B=∠E,∠C =∠F,BC=EF
2.如D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,若AB=4,CF=3,则BD的长是( )
A.0.5 B.1 C.1.5 D.2
3.如OC=OD=8,∠C=∠D,BC=6,OA=4,则AD等于( )
A.6 B.5 C.4 D.3
4.如点P在∠AOB的平分线上,∠APO=∠BPO,那么根据 可判定△AOP≌△BOP.
5.如已知∠B=∠DEF,BC=EF,现要证明△ABC≌△DEF,若要直接以“ASA”为依据,则可添加条件: .
6.[2019·朝阳期末] 已知:如D是BC上的一点,AB=BD,DE∥AB,∠A=∠DBE.
求证:AC=BE.
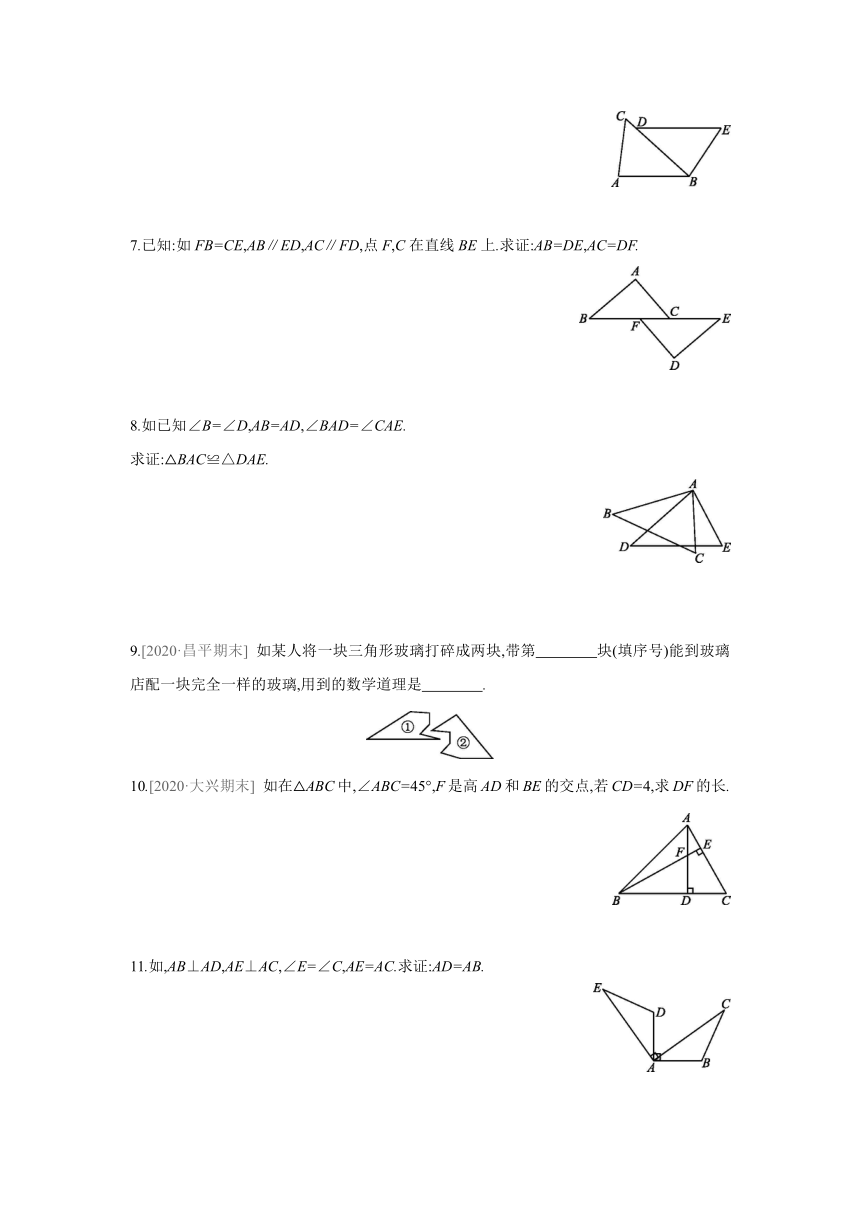
7.已知:如FB=CE,AB∥ED,AC∥FD,点F,C在直线BE上.求证:AB=DE,AC=DF.
8.如已知∠B=∠D,AB=AD,∠BAD=∠CAE.
求证:△BAC≌△DAE.
9.[2020·昌平期末] 如某人将一块三角形玻璃打碎成两块,带第 块(填序号)能到玻璃店配一块完全一样的玻璃,用到的数学道理是 .
10.[2020·大兴期末] 如在△ABC中,∠ABC=45°,F是高AD和BE的交点,若CD=4,求DF的长.
11.如,AB⊥AD,AE⊥AC,∠E=∠C,AE=AC.求证:AD=AB.
12.如,已知AE=BF,AD∥BC,AD=BC,AB,CD交于点O.求证:OE=OF.
13.如,在△ABC中,∠ABC=90°,BD⊥AC于点D,点E在BC的延长线上,且BE=AB,过点E作EF⊥BE,与BD的延长线交于点F.求证:BC=EF.
答案
1.C 2.B 3.A
4.ASA 5.∠ACB=∠F
6.证明:∵DE∥AB,
∴∠ABC=∠BDE.
在△ABC和△BDE中,
∴△ABC≌△BDE.
∴AC=BE.
7.证明:∵FB=CE,
∴FB+FC=CE+FC,
即 BC=EF.
∵AB∥ED,
∴∠B=∠E.
∵AC∥FD,
∴∠ACB=∠DFE.
在△ABC和△DEF中,
∴△ABC≌△DEF(ASA).
∴AB=DE,AC=DF(全等三角形的对应边相等).
8.证明:∵∠BAD=∠CAE,∴∠BAC=∠DAE.
在△BAC和△DAE中,
∴△BAC≌△DAE(ASA).
9.② ASA
10.解:∵AD是△ABC的高,
∴∠ADB=∠ADC=90°.
∵∠ABC=45°,∴∠BAD=∠ABC=45°,
∴BD=AD.
∵BE是△ABC的高,∴∠BEC=90°,
∴∠DBF+∠C=90°.
∵∠ADC=90°,∴∠DAC+∠C=90°,
∴∠DBF=∠DAC.
在△BDF和△ADC中,
∴△BDF≌△ADC,∴DF=CD.
∵CD=4,∴DF=4.
11.证明:∵AB⊥AD,AE⊥AC,
∴∠EAC=∠DAB=90°,
即∠EAD+∠DAC=∠CAB+∠DAC.
∴∠EAD=∠CAB.
在△ADE和△ABC中,
∴△ADE≌△ABC(ASA).
∴AD=AB.
12.证明:∵AD∥BC,
∴∠A=∠B,∠ADO=∠BCO.
在△ADO和△BCO中,
∴△ADO≌△BCO (ASA).
∴AO=BO.
又∵AE=BF,
∴OE=OF.
13.证明:∵∠ABC=90°,BD⊥AC,EF⊥BE,
∴∠ABC=∠BEF=∠ADB=90°.
∴∠A+∠ABD=∠FBE+∠ABD=90°.
∴∠A=∠FBE.
在△ABC和△BEF中,
∴△ABC≌△BEF(ASA).
∴BC=EF.
有两角和它们的夹边分别相等的两个三角形全等(简记为:角边角或ASA).
1.下列条件中,不能判定△ABC≌△DEF的是( )
A.∠A=∠D,∠C =∠F,AC=DF
B.∠A=∠D,∠B =∠E,AB=DE
C.∠A=∠B,∠D =∠E,AD=BE
D.∠B=∠E,∠C =∠F,BC=EF
2.如D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,若AB=4,CF=3,则BD的长是( )
A.0.5 B.1 C.1.5 D.2
3.如OC=OD=8,∠C=∠D,BC=6,OA=4,则AD等于( )
A.6 B.5 C.4 D.3
4.如点P在∠AOB的平分线上,∠APO=∠BPO,那么根据 可判定△AOP≌△BOP.
5.如已知∠B=∠DEF,BC=EF,现要证明△ABC≌△DEF,若要直接以“ASA”为依据,则可添加条件: .
6.[2019·朝阳期末] 已知:如D是BC上的一点,AB=BD,DE∥AB,∠A=∠DBE.
求证:AC=BE.
7.已知:如FB=CE,AB∥ED,AC∥FD,点F,C在直线BE上.求证:AB=DE,AC=DF.
8.如已知∠B=∠D,AB=AD,∠BAD=∠CAE.
求证:△BAC≌△DAE.
9.[2020·昌平期末] 如某人将一块三角形玻璃打碎成两块,带第 块(填序号)能到玻璃店配一块完全一样的玻璃,用到的数学道理是 .
10.[2020·大兴期末] 如在△ABC中,∠ABC=45°,F是高AD和BE的交点,若CD=4,求DF的长.
11.如,AB⊥AD,AE⊥AC,∠E=∠C,AE=AC.求证:AD=AB.
12.如,已知AE=BF,AD∥BC,AD=BC,AB,CD交于点O.求证:OE=OF.
13.如,在△ABC中,∠ABC=90°,BD⊥AC于点D,点E在BC的延长线上,且BE=AB,过点E作EF⊥BE,与BD的延长线交于点F.求证:BC=EF.
答案
1.C 2.B 3.A
4.ASA 5.∠ACB=∠F
6.证明:∵DE∥AB,
∴∠ABC=∠BDE.
在△ABC和△BDE中,
∴△ABC≌△BDE.
∴AC=BE.
7.证明:∵FB=CE,
∴FB+FC=CE+FC,
即 BC=EF.
∵AB∥ED,
∴∠B=∠E.
∵AC∥FD,
∴∠ACB=∠DFE.
在△ABC和△DEF中,
∴△ABC≌△DEF(ASA).
∴AB=DE,AC=DF(全等三角形的对应边相等).
8.证明:∵∠BAD=∠CAE,∴∠BAC=∠DAE.
在△BAC和△DAE中,
∴△BAC≌△DAE(ASA).
9.② ASA
10.解:∵AD是△ABC的高,
∴∠ADB=∠ADC=90°.
∵∠ABC=45°,∴∠BAD=∠ABC=45°,
∴BD=AD.
∵BE是△ABC的高,∴∠BEC=90°,
∴∠DBF+∠C=90°.
∵∠ADC=90°,∴∠DAC+∠C=90°,
∴∠DBF=∠DAC.
在△BDF和△ADC中,
∴△BDF≌△ADC,∴DF=CD.
∵CD=4,∴DF=4.
11.证明:∵AB⊥AD,AE⊥AC,
∴∠EAC=∠DAB=90°,
即∠EAD+∠DAC=∠CAB+∠DAC.
∴∠EAD=∠CAB.
在△ADE和△ABC中,
∴△ADE≌△ABC(ASA).
∴AD=AB.
12.证明:∵AD∥BC,
∴∠A=∠B,∠ADO=∠BCO.
在△ADO和△BCO中,
∴△ADO≌△BCO (ASA).
∴AO=BO.
又∵AE=BF,
∴OE=OF.
13.证明:∵∠ABC=90°,BD⊥AC,EF⊥BE,
∴∠ABC=∠BEF=∠ADB=90°.
∴∠A+∠ABD=∠FBE+∠ABD=90°.
∴∠A=∠FBE.
在△ABC和△BEF中,
∴△ABC≌△BEF(ASA).
∴BC=EF.
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
