北京课改版数学八年级上册同步课时练习:12.5.2 边角边公理(word版含答案)
文档属性
| 名称 | 北京课改版数学八年级上册同步课时练习:12.5.2 边角边公理(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 185.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-17 21:00:04 | ||
图片预览


文档简介
第2课时 边角边公理
有两边和它们的夹角分别相等的两个三角形全等(简记为:边角边或SAS).
1.如,线段AB,CD互相平分且交于点O,则下列结论错误的是( )
A.AD=BC B.∠C=∠D
C.AD∥BC D.OC=OB
2.如所示,D是BC的中点,AD⊥BC,那么下列说法错误的是( )
A.△ABD≌△ACD B.∠B=∠C
C.AD平分∠BAC D.AD=BD
3.在△ABC和△DEF中,已知AB=4,BC=6,∠B=60°,DE=6,FD=4,∠E+∠F=120°,则△ABC与△DEF的关系是( )
A.△ABC与△DEF不全等
B.△ABC≌△DEF
C.△ABC≌△FDE
D.无法确定
4.如所示,点D在AB上,点E在AC上,CD与BE交于点O,且AD=AE,AB=AC,若
∠B=20°,则∠C= °.
5.如所示,将两根钢条AA',BB'的中点O连在一起,使AA',BB'可以绕着点O自由转动,就做成了一个测量工具,则A'B'的长等于内槽宽AB,那么判定△OAB≌△OA'B'的理由是 .
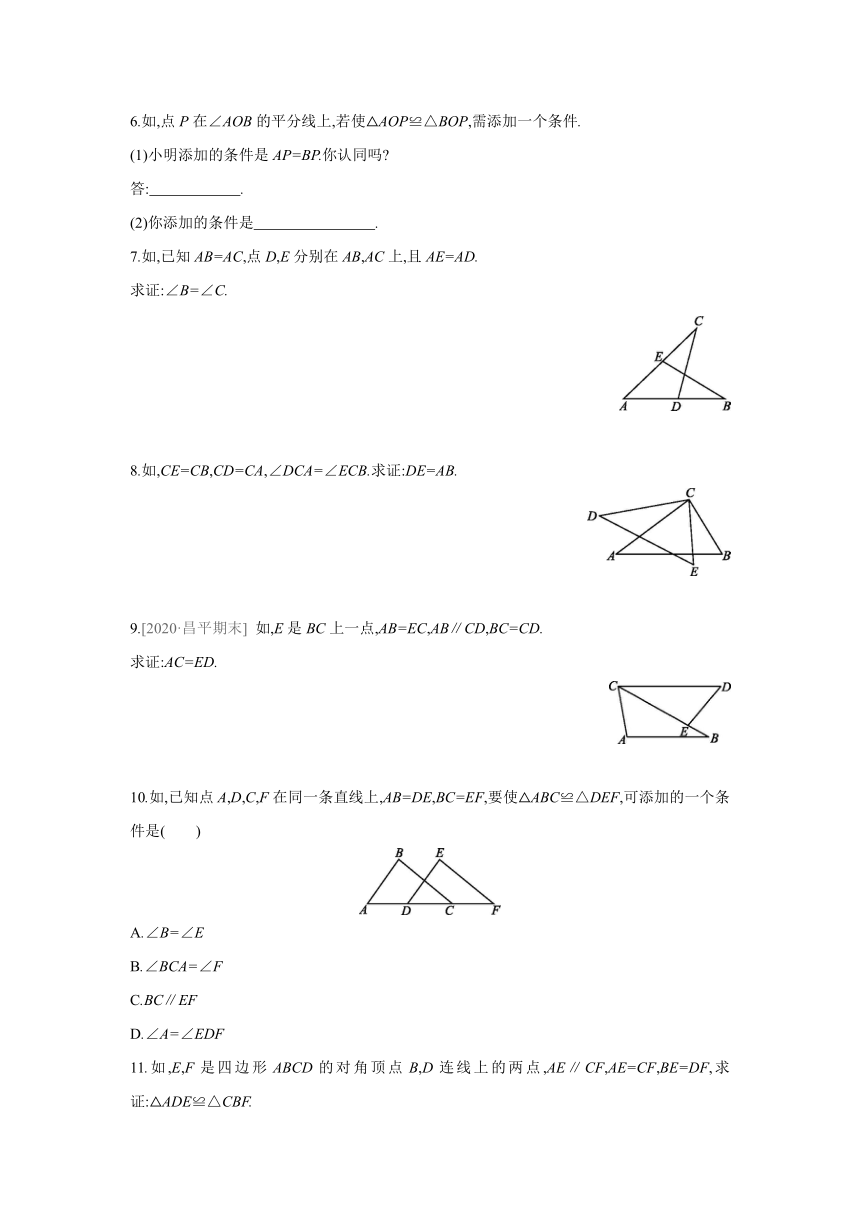
6.如,点P在∠AOB的平分线上,若使△AOP≌△BOP,需添加一个条件.
(1)小明添加的条件是AP=BP.你认同吗
答: .
(2)你添加的条件是 .
7.如,已知AB=AC,点D,E分别在AB,AC上,且AE=AD.
求证:∠B=∠C.
8.如,CE=CB,CD=CA,∠DCA=∠ECB.求证:DE=AB.
9.[2020·昌平期末] 如,E是BC上一点,AB=EC,AB∥CD,BC=CD.
求证:AC=ED.
10.如,已知点A,D,C,F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,可添加的一个条件是( )
A.∠B=∠E
B.∠BCA=∠F
C.BC∥EF
D.∠A=∠EDF
11.如,E,F是四边形ABCD的对角顶点B,D连线上的两点,AE∥CF,AE=CF,BE=DF,求证:△ADE≌△CBF.
12.已知:如,在△ABC中,∠B=∠C,BD=CF,BE=CD.
求证:∠EDF=∠B.
13.如,在Rt△ABC中,∠BAC=90°,AC=2AB,D是AC的中点,将一块锐角为45°的三角尺ADE如放置,三角尺斜边的两个端点恰好分别与点A,D重合,连接BE,CE.试猜想线段BE和CE的数量及位置关系,并证明你的猜想.
14.[2020·大兴期末] 已知:如,在Rt△ABC中,∠ACB=90°,AC=BC,D是线段AB上一点,连接CD,将线段CD绕点C逆时针旋转90°得到线段CE,连接DE,BE.
(1)依题意补全形;
(2)若∠ACD=α,用含α的代数式表示∠DEB.
答案
1.D
2.D 因为D为BC的中点,且AD⊥BC,所以BD=DC,∠ADB=∠ADC=90°,易证
△ADB≌△ADC(SAS),所以∠B=∠C,∠BAD=∠CAD,而AD=BD不能确定.
3.C 由∠E+∠F=120°,可得∠D=60°,
∴∠B=∠D.
又AB=FD,BC=DE,
故△ABC≌△FDE.
4.20 易证△ABE≌△ACD,所以∠C=∠B=20°.
5.SAS
6.(1)不认同
(2)AO=BO(答案不唯一)
7.证明:在△ABE和△ACD中,
∴△ABE≌△ACD(SAS).
∴∠B=∠C.
8.证明:∵∠DCA=∠ECB,
∴∠DCA+∠ACE=∠ECB+∠ACE,
即∠DCE=∠ACB.
在△DCE和△ACB中,
∴△DCE≌△ACB(SAS).
∴DE=AB.
9.证明:∵AB∥CD,∴∠CBA=∠DCE.
在△BAC和△CED中,
∴△BAC≌△CED(SAS).
∴AC=ED.
10.A
11.证明:∵BE=DF,
∴BF=DE.
∵AE∥CF,∴∠AED=∠CFB.
在△ADE和△CBF中,
∴△ADE≌△CBF.
12.证明:在△BDE和△CFD中,
∴△BDE≌△CFD(SAS).
∴∠BED=∠CDF.
∵∠EDC=∠EDF+∠CDF=∠B+∠BED,
∴∠EDF=∠B.
13.解:BE=CE,BE⊥CE.
证明:∵AC=2AB,D是AC的中点,
∴AB=AD=DC.
∵∠EAD=∠EDA=45°,
∴∠EAB=∠EDC=135°.
在△EAB和△EDC中,
∴△EAB≌△EDC(SAS).
∴∠AEB=∠DEC,BE=CE.
∴∠BEC=∠AED=90°.
故BE=CE,BE⊥CE.
14.解:(1)补全形如所示.
(2)∵将线段CD绕点C逆时针旋转90°得到线段CE,
∴∠DCE=90°,CD=CE.
∵∠ACB=90°,∴∠ACD=∠BCE.
在△ACD和△BCE中,
∴△ACD≌△BCE,
∴∠CBE=∠A.
∵∠ACB=90°,AC=BC,
∴∠A=45°,∴∠CBE=45°.
∵∠DCE=90°,CD=CE,
∴∠CED=45°.
在△BCE中,∠BCE=∠ACD=α.
∴∠DEB=180°-α-45°-45°=90°-α.
有两边和它们的夹角分别相等的两个三角形全等(简记为:边角边或SAS).
1.如,线段AB,CD互相平分且交于点O,则下列结论错误的是( )
A.AD=BC B.∠C=∠D
C.AD∥BC D.OC=OB
2.如所示,D是BC的中点,AD⊥BC,那么下列说法错误的是( )
A.△ABD≌△ACD B.∠B=∠C
C.AD平分∠BAC D.AD=BD
3.在△ABC和△DEF中,已知AB=4,BC=6,∠B=60°,DE=6,FD=4,∠E+∠F=120°,则△ABC与△DEF的关系是( )
A.△ABC与△DEF不全等
B.△ABC≌△DEF
C.△ABC≌△FDE
D.无法确定
4.如所示,点D在AB上,点E在AC上,CD与BE交于点O,且AD=AE,AB=AC,若
∠B=20°,则∠C= °.
5.如所示,将两根钢条AA',BB'的中点O连在一起,使AA',BB'可以绕着点O自由转动,就做成了一个测量工具,则A'B'的长等于内槽宽AB,那么判定△OAB≌△OA'B'的理由是 .
6.如,点P在∠AOB的平分线上,若使△AOP≌△BOP,需添加一个条件.
(1)小明添加的条件是AP=BP.你认同吗
答: .
(2)你添加的条件是 .
7.如,已知AB=AC,点D,E分别在AB,AC上,且AE=AD.
求证:∠B=∠C.
8.如,CE=CB,CD=CA,∠DCA=∠ECB.求证:DE=AB.
9.[2020·昌平期末] 如,E是BC上一点,AB=EC,AB∥CD,BC=CD.
求证:AC=ED.
10.如,已知点A,D,C,F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,可添加的一个条件是( )
A.∠B=∠E
B.∠BCA=∠F
C.BC∥EF
D.∠A=∠EDF
11.如,E,F是四边形ABCD的对角顶点B,D连线上的两点,AE∥CF,AE=CF,BE=DF,求证:△ADE≌△CBF.
12.已知:如,在△ABC中,∠B=∠C,BD=CF,BE=CD.
求证:∠EDF=∠B.
13.如,在Rt△ABC中,∠BAC=90°,AC=2AB,D是AC的中点,将一块锐角为45°的三角尺ADE如放置,三角尺斜边的两个端点恰好分别与点A,D重合,连接BE,CE.试猜想线段BE和CE的数量及位置关系,并证明你的猜想.
14.[2020·大兴期末] 已知:如,在Rt△ABC中,∠ACB=90°,AC=BC,D是线段AB上一点,连接CD,将线段CD绕点C逆时针旋转90°得到线段CE,连接DE,BE.
(1)依题意补全形;
(2)若∠ACD=α,用含α的代数式表示∠DEB.
答案
1.D
2.D 因为D为BC的中点,且AD⊥BC,所以BD=DC,∠ADB=∠ADC=90°,易证
△ADB≌△ADC(SAS),所以∠B=∠C,∠BAD=∠CAD,而AD=BD不能确定.
3.C 由∠E+∠F=120°,可得∠D=60°,
∴∠B=∠D.
又AB=FD,BC=DE,
故△ABC≌△FDE.
4.20 易证△ABE≌△ACD,所以∠C=∠B=20°.
5.SAS
6.(1)不认同
(2)AO=BO(答案不唯一)
7.证明:在△ABE和△ACD中,
∴△ABE≌△ACD(SAS).
∴∠B=∠C.
8.证明:∵∠DCA=∠ECB,
∴∠DCA+∠ACE=∠ECB+∠ACE,
即∠DCE=∠ACB.
在△DCE和△ACB中,
∴△DCE≌△ACB(SAS).
∴DE=AB.
9.证明:∵AB∥CD,∴∠CBA=∠DCE.
在△BAC和△CED中,
∴△BAC≌△CED(SAS).
∴AC=ED.
10.A
11.证明:∵BE=DF,
∴BF=DE.
∵AE∥CF,∴∠AED=∠CFB.
在△ADE和△CBF中,
∴△ADE≌△CBF.
12.证明:在△BDE和△CFD中,
∴△BDE≌△CFD(SAS).
∴∠BED=∠CDF.
∵∠EDC=∠EDF+∠CDF=∠B+∠BED,
∴∠EDF=∠B.
13.解:BE=CE,BE⊥CE.
证明:∵AC=2AB,D是AC的中点,
∴AB=AD=DC.
∵∠EAD=∠EDA=45°,
∴∠EAB=∠EDC=135°.
在△EAB和△EDC中,
∴△EAB≌△EDC(SAS).
∴∠AEB=∠DEC,BE=CE.
∴∠BEC=∠AED=90°.
故BE=CE,BE⊥CE.
14.解:(1)补全形如所示.
(2)∵将线段CD绕点C逆时针旋转90°得到线段CE,
∴∠DCE=90°,CD=CE.
∵∠ACB=90°,∴∠ACD=∠BCE.
在△ACD和△BCE中,
∴△ACD≌△BCE,
∴∠CBE=∠A.
∵∠ACB=90°,AC=BC,
∴∠A=45°,∴∠CBE=45°.
∵∠DCE=90°,CD=CE,
∴∠CED=45°.
在△BCE中,∠BCE=∠ACD=α.
∴∠DEB=180°-α-45°-45°=90°-α.
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
