北京课改版数学八年级上册同步课时练习:12.6.1 等腰三角形(word版含答案)
文档属性
| 名称 | 北京课改版数学八年级上册同步课时练习:12.6.1 等腰三角形(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 153.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-17 00:00:00 | ||
图片预览


文档简介
12.6.1 等腰三角形
1.等腰三角形的概念:有两条边相等的三角形叫做等腰三角形.相等的两条边叫做腰,另一边叫做底.
2.三角形按边分类:
三角形
1.[2020·大兴期末] 若一个等腰三角形的两边长分别为4,5,则这个等腰三角形的周长为( )
A.13 B.14
C.13或14 D.8或10
2.在等腰三角形ABC中,已知AB=2BC,AB=20,则△ABC的周长为( )
A.40 B.50
C.40或50 D.无法确定
3.若等腰三角形一腰上的中线把等腰三角形的周长分成9和12两部分,则腰长为( )
A.6 B.8 C.10 D.6或8
4.[2020·昌平期末] 已知等腰三角形的周长为20 cm,其中一边的长为6 cm,则底边的长为 .
5.若等边三角形的边长为a,则它的周长为 .
6.若等腰三角形的底边长是8,则它的腰长x的取值范围是 .
7.如示,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,写出中的等腰三角形: .
8.已知等腰三角形的周长为16,其一边长为6,求另两边长.
9.在等腰三角形ABC中,AB=AC,周长为14 cm,AC边上的中线BD把△ABC分成了周长差为4 cm的两个三角形,求△ABC的各边长.
10.等腰三角形一腰上的高与另一腰的夹角为48°,则该等腰三角形底角的度数为 .
11.某个等腰三角形的周长为5,且它的三边长都是整数,则底边长为 .
12. 已知等腰三角形的底边长为5 cm,一腰上的中线把其周长分成差为3 cm的两部分,求这个等腰三角形的腰长.
13.已知等腰三角形ABC的周长为42 cm,其中一边与另一边的长度比为3 ∶ 2,求△ABC各边的长.
14.若等腰三角形的周长为19 cm,其中一边长为5 cm,求该等腰三角形的底边长.
15.在平面内,分别用3根、5根、6根……火柴首尾依次相接,能搭成什么形状的三角形呢 通过尝试,列表如下,请阅读下表后再回答问题:
火柴根数 3 5 6
示意
形状 等边三角形 等腰三角形 等边三角形
(1)4根火柴能搭成三角形吗
(2)8根、12根火柴分别能搭成几种等腰(等边)三角形 画出它们的示意.
“串”题训练 正方形网格背景下等腰三角形的构建
方法指引:
网格背景中的每个小正方形的边长都相等,且网格线互相垂直,根据这些隐含条件,利用边角边可得三角形全等,进而判断不与网格线重合的其他线段相等.
例:如示的正方形网格中,网格线的交点称为格点.已知A,B是两个格点,如果C也是中的格点,且使得△ABC为等腰三角形,那么点C的个数是( )
A.6 B.7 C.8 D.9
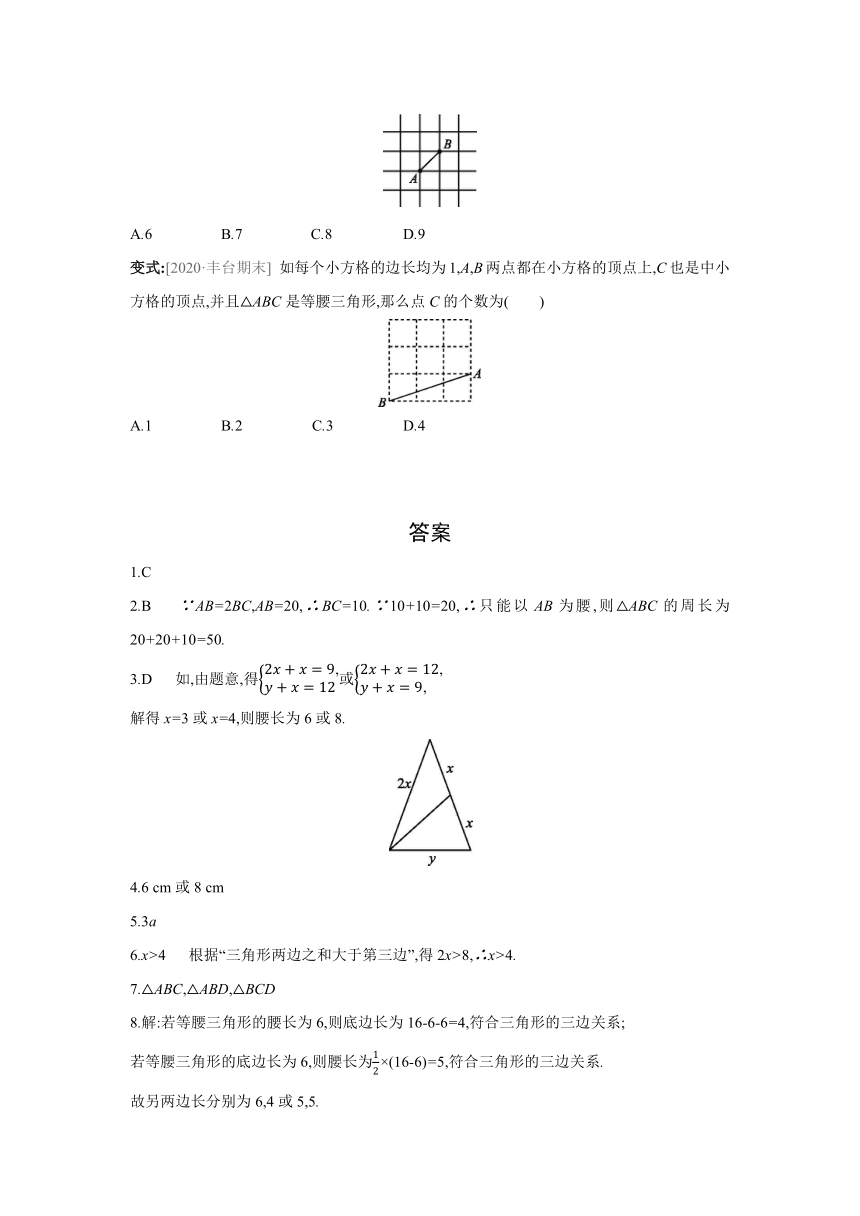
变式:[2020·丰台期末] 如每个小方格的边长均为1,A,B两点都在小方格的顶点上,C也是中小方格的顶点,并且△ABC是等腰三角形,那么点C的个数为( )
A.1 B.2 C.3 D.4
答案
1.C
2.B ∵AB=2BC,AB=20,∴BC=10.∵10+10=20,∴只能以AB为腰,则△ABC的周长为20+20+10=50.
3.D 如,由题意,得或
解得x=3或x=4,则腰长为6或8.
4.6 cm或8 cm
5.3a
6.x>4 根据“三角形两边之和大于第三边”,得2x>8,∴x>4.
7.△ABC,△ABD,△BCD
8.解:若等腰三角形的腰长为6,则底边长为16-6-6=4,符合三角形的三边关系;
若等腰三角形的底边长为6,则腰长为×(16-6)=5,符合三角形的三边关系.
故另两边长分别为6,4或5,5.
9.解:如所示.设AD=x cm,BC=y cm,则DC=x cm,AB=2x cm.
由题意列方程组,得或
解得或
显然第二种情况不符合“三角形两边之和大于第三边”,所以舍去.
所以△ABC的三边长分别为AB=AC=6 cm,BC=2 cm.
10.69°或21° 分两种情况讨论:
(1)若∠BAC<90°,如①所示.
∵BD⊥AC,
∴∠A+∠ABD=90°.
∵∠ABD=48°,
∴∠A=90°-48°=42°.
∵AB=AC,
∴∠ABC=∠C=×(180°-42°)=69°.
(2)若∠BAC>90°,如②所示.
同(1)可得∠DAB=90°-48°=42°.
∵AB=AC,∴∠ABC=∠C=×42°=21°.
综上所述,等腰三角形底角的度数为69°或21°.
11.1 若三边长分别为1,1,3,不符合三角形的三边关系;若三边长分别为1,2,2,符合三角形的三边关系.
12.解:如,BD把△ABC的周长分成AB+AD与BC+CD两部分,由于AD=CD,则=3 cm.
若AB-BC=3 cm,即等腰三角形的腰长为8 cm,底边长为5 cm,此时能构成三角形;
若BC-AB=3 cm,即等腰三角形的腰长为2 cm,底边长为5 cm,此时不能构成三角形.
故这个等腰三角形的腰长为8 cm.
13.解:(1)设三角形的底边长为3x cm,则其腰长为2x cm.
由题意,得3x+2x+2x=42,解得x=6,
所以△ABC的三边长分别为18 cm,12 cm,12 cm.
(2)设三角形的底边长为2x cm,则其腰长为3x cm.
由题意,得2x+3x+3x=42,解得x=5.25,
所以△ABC的三边长分别为10.5 cm,15.75 cm,15.75 cm.
综上,△ABC各边的长分别为18 cm,12 cm,12 cm或10.5 cm,15.75 cm,15.75 cm.
14.解:若等腰三角形的腰长为5 cm,则底边长为19-5-5=9(cm),符合三角形的三边关系.
若等腰三角形的底边长为5 cm,则腰长为×(19-5)=7(cm),符合三角形的三边关系.
故该等腰三角形的底边长为9 cm或5 cm.
15.解:(1)不能.
(2)8根火柴能搭成一种等腰三角形,边长分别是2,3,3;
12根火柴能搭成一种等腰三角形,一种等边三角形,边长分别是2,5,5(等腰三角形)和4,4,4(等边三角形).
画示意略.
“串”题训练
例:C
变式:C 点C的位置如所示.
1.等腰三角形的概念:有两条边相等的三角形叫做等腰三角形.相等的两条边叫做腰,另一边叫做底.
2.三角形按边分类:
三角形
1.[2020·大兴期末] 若一个等腰三角形的两边长分别为4,5,则这个等腰三角形的周长为( )
A.13 B.14
C.13或14 D.8或10
2.在等腰三角形ABC中,已知AB=2BC,AB=20,则△ABC的周长为( )
A.40 B.50
C.40或50 D.无法确定
3.若等腰三角形一腰上的中线把等腰三角形的周长分成9和12两部分,则腰长为( )
A.6 B.8 C.10 D.6或8
4.[2020·昌平期末] 已知等腰三角形的周长为20 cm,其中一边的长为6 cm,则底边的长为 .
5.若等边三角形的边长为a,则它的周长为 .
6.若等腰三角形的底边长是8,则它的腰长x的取值范围是 .
7.如示,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,写出中的等腰三角形: .
8.已知等腰三角形的周长为16,其一边长为6,求另两边长.
9.在等腰三角形ABC中,AB=AC,周长为14 cm,AC边上的中线BD把△ABC分成了周长差为4 cm的两个三角形,求△ABC的各边长.
10.等腰三角形一腰上的高与另一腰的夹角为48°,则该等腰三角形底角的度数为 .
11.某个等腰三角形的周长为5,且它的三边长都是整数,则底边长为 .
12. 已知等腰三角形的底边长为5 cm,一腰上的中线把其周长分成差为3 cm的两部分,求这个等腰三角形的腰长.
13.已知等腰三角形ABC的周长为42 cm,其中一边与另一边的长度比为3 ∶ 2,求△ABC各边的长.
14.若等腰三角形的周长为19 cm,其中一边长为5 cm,求该等腰三角形的底边长.
15.在平面内,分别用3根、5根、6根……火柴首尾依次相接,能搭成什么形状的三角形呢 通过尝试,列表如下,请阅读下表后再回答问题:
火柴根数 3 5 6
示意
形状 等边三角形 等腰三角形 等边三角形
(1)4根火柴能搭成三角形吗
(2)8根、12根火柴分别能搭成几种等腰(等边)三角形 画出它们的示意.
“串”题训练 正方形网格背景下等腰三角形的构建
方法指引:
网格背景中的每个小正方形的边长都相等,且网格线互相垂直,根据这些隐含条件,利用边角边可得三角形全等,进而判断不与网格线重合的其他线段相等.
例:如示的正方形网格中,网格线的交点称为格点.已知A,B是两个格点,如果C也是中的格点,且使得△ABC为等腰三角形,那么点C的个数是( )
A.6 B.7 C.8 D.9
变式:[2020·丰台期末] 如每个小方格的边长均为1,A,B两点都在小方格的顶点上,C也是中小方格的顶点,并且△ABC是等腰三角形,那么点C的个数为( )
A.1 B.2 C.3 D.4
答案
1.C
2.B ∵AB=2BC,AB=20,∴BC=10.∵10+10=20,∴只能以AB为腰,则△ABC的周长为20+20+10=50.
3.D 如,由题意,得或
解得x=3或x=4,则腰长为6或8.
4.6 cm或8 cm
5.3a
6.x>4 根据“三角形两边之和大于第三边”,得2x>8,∴x>4.
7.△ABC,△ABD,△BCD
8.解:若等腰三角形的腰长为6,则底边长为16-6-6=4,符合三角形的三边关系;
若等腰三角形的底边长为6,则腰长为×(16-6)=5,符合三角形的三边关系.
故另两边长分别为6,4或5,5.
9.解:如所示.设AD=x cm,BC=y cm,则DC=x cm,AB=2x cm.
由题意列方程组,得或
解得或
显然第二种情况不符合“三角形两边之和大于第三边”,所以舍去.
所以△ABC的三边长分别为AB=AC=6 cm,BC=2 cm.
10.69°或21° 分两种情况讨论:
(1)若∠BAC<90°,如①所示.
∵BD⊥AC,
∴∠A+∠ABD=90°.
∵∠ABD=48°,
∴∠A=90°-48°=42°.
∵AB=AC,
∴∠ABC=∠C=×(180°-42°)=69°.
(2)若∠BAC>90°,如②所示.
同(1)可得∠DAB=90°-48°=42°.
∵AB=AC,∴∠ABC=∠C=×42°=21°.
综上所述,等腰三角形底角的度数为69°或21°.
11.1 若三边长分别为1,1,3,不符合三角形的三边关系;若三边长分别为1,2,2,符合三角形的三边关系.
12.解:如,BD把△ABC的周长分成AB+AD与BC+CD两部分,由于AD=CD,则=3 cm.
若AB-BC=3 cm,即等腰三角形的腰长为8 cm,底边长为5 cm,此时能构成三角形;
若BC-AB=3 cm,即等腰三角形的腰长为2 cm,底边长为5 cm,此时不能构成三角形.
故这个等腰三角形的腰长为8 cm.
13.解:(1)设三角形的底边长为3x cm,则其腰长为2x cm.
由题意,得3x+2x+2x=42,解得x=6,
所以△ABC的三边长分别为18 cm,12 cm,12 cm.
(2)设三角形的底边长为2x cm,则其腰长为3x cm.
由题意,得2x+3x+3x=42,解得x=5.25,
所以△ABC的三边长分别为10.5 cm,15.75 cm,15.75 cm.
综上,△ABC各边的长分别为18 cm,12 cm,12 cm或10.5 cm,15.75 cm,15.75 cm.
14.解:若等腰三角形的腰长为5 cm,则底边长为19-5-5=9(cm),符合三角形的三边关系.
若等腰三角形的底边长为5 cm,则腰长为×(19-5)=7(cm),符合三角形的三边关系.
故该等腰三角形的底边长为9 cm或5 cm.
15.解:(1)不能.
(2)8根火柴能搭成一种等腰三角形,边长分别是2,3,3;
12根火柴能搭成一种等腰三角形,一种等边三角形,边长分别是2,5,5(等腰三角形)和4,4,4(等边三角形).
画示意略.
“串”题训练
例:C
变式:C 点C的位置如所示.
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
