北京课改版数学八年级上册同步课时练习:12.6.2 第2课时 三线合一(word版含答案)
文档属性
| 名称 | 北京课改版数学八年级上册同步课时练习:12.6.2 第2课时 三线合一(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 168.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-17 00:00:00 | ||
图片预览


文档简介
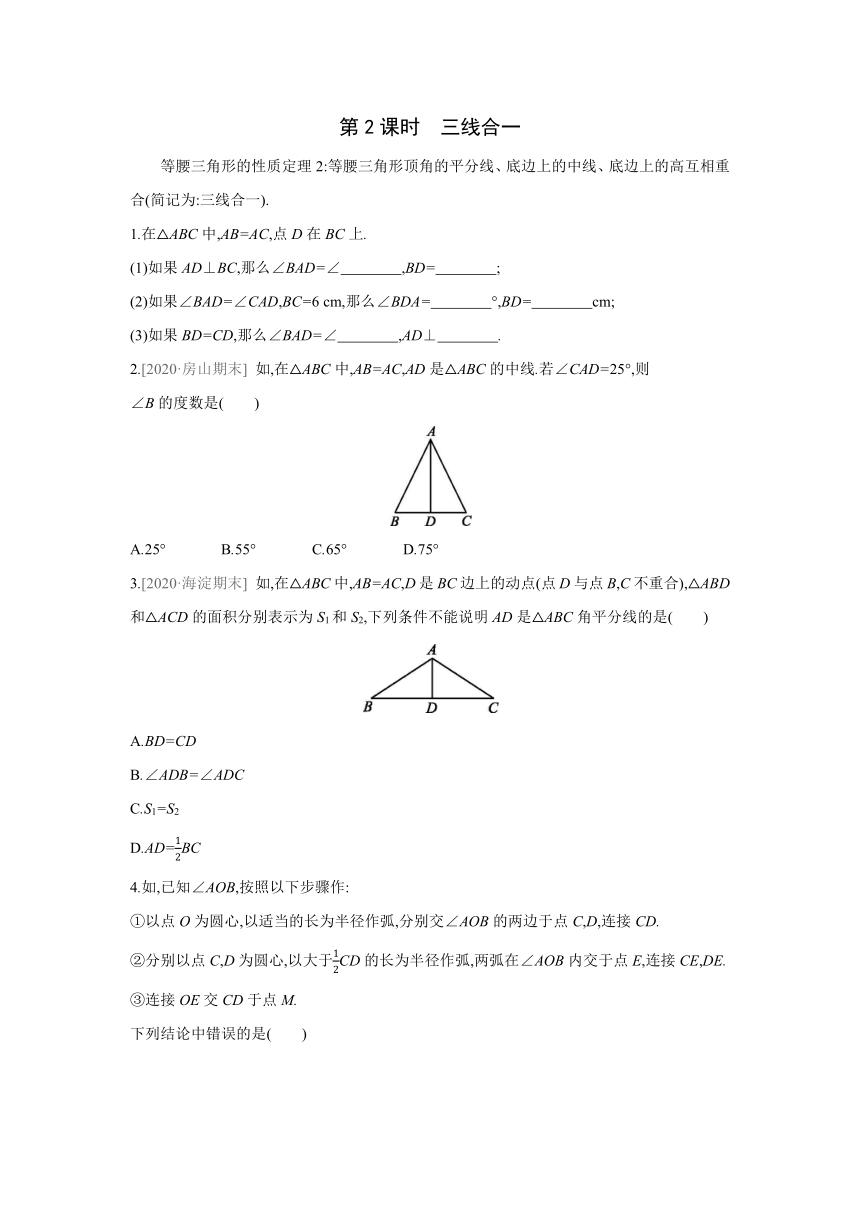
第2课时 三线合一
等腰三角形的性质定理2:等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合(简记为:三线合一).
1.在△ABC中,AB=AC,点D在BC上.
(1)如果AD⊥BC,那么∠BAD=∠ ,BD= ;
(2)如果∠BAD=∠CAD,BC=6 cm,那么∠BDA= °,BD= cm;
(3)如果BD=CD,那么∠BAD=∠ ,AD⊥ .
2.[2020·房山期末] 如,在△ABC中,AB=AC,AD是△ABC的中线.若∠CAD=25°,则
∠B的度数是( )
A.25° B.55° C.65° D.75°
3.[2020·海淀期末] 如,在△ABC中,AB=AC,D是BC边上的动点(点D与点B,C不重合),△ABD和△ACD的面积分别表示为S1和S2,下列条件不能说明AD是△ABC角平分线的是( )
A.BD=CD
B.∠ADB=∠ADC
C.S1=S2
D.AD=BC
4.如,已知∠AOB,按照以下步骤作:
①以点O为圆心,以适当的长为半径作弧,分别交∠AOB的两边于点C,D,连接CD.
②分别以点C,D为圆心,以大于CD的长为半径作弧,两弧在∠AOB内交于点E,连接CE,DE.
③连接OE交CD于点M.
下列结论中错误的是( )
A.∠CEO=∠DEO B.CM=MD
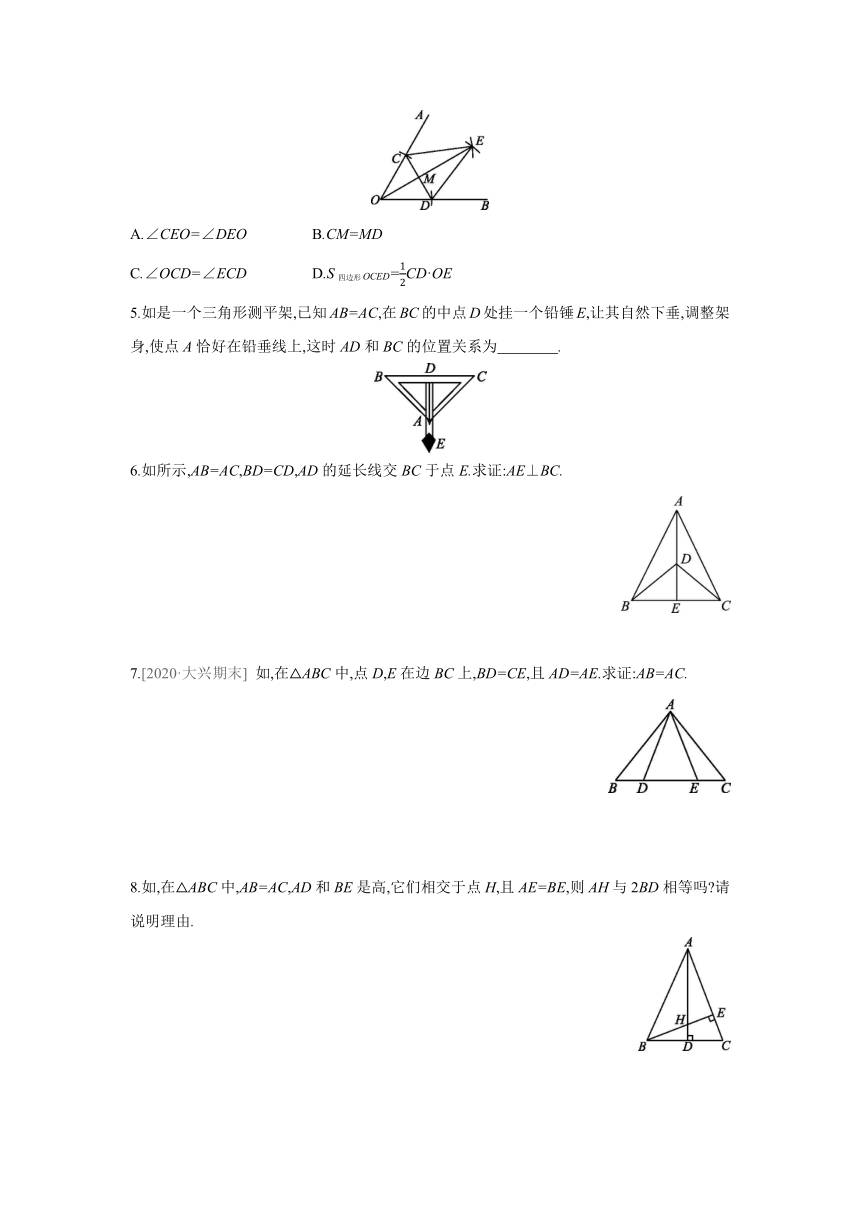
C.∠OCD=∠ECD D.S四边形OCED=CD·OE
5.如是一个三角形测平架,已知AB=AC,在BC的中点D处挂一个铅锤E,让其自然下垂,调整架身,使点A恰好在铅垂线上,这时AD和BC的位置关系为 .
6.如所示,AB=AC,BD=CD,AD的延长线交BC于点E.求证:AE⊥BC.
7.[2020·大兴期末] 如,在△ABC中,点D,E在边BC上,BD=CE,且AD=AE.求证:AB=AC.
8.如,在△ABC中,AB=AC,AD和BE是高,它们相交于点H,且AE=BE,则AH与2BD相等吗 请说明理由.
9.如,在等腰三角形ABC中,AB=AC,AD是BC边上的中线,∠ABC的平分线BG交AD于点E,EF⊥AB,垂足为F.
求证:EF=ED.
10.如,已知AB=AC,BD⊥AC,垂足为D.求证:∠DBC=∠A.
11.如,在△ABC中,AB=AC,点D在BA的延长线上,点E在AC上,且AD=AE.求证:DE⊥BC.
12.在△ABC中,AB=AC,∠1=∠ABC,∠2=∠ACB,BD与CE相交于点O,如,∠BOC的大小与∠A的大小有什么关系
若∠1=∠ABC,∠2=∠ACB,则∠BOC与∠A的大小关系如何
若∠1=∠ABC,∠2=∠ACB,则∠BOC与∠A的大小关系如何
答案
1.(1)CAD CD (2)90 3 (3)CAD BC
等腰三角形三线合一的性质.
2.C
3.D
4.C
5.AD⊥BC
6.证明:在△BAD与△CAD中,
∴△BAD≌△CAD(SSS).
∴∠BAE=∠CAE.
又∵AB=AC,∴AE⊥BC.
7.证明:过点A作AF⊥BC于点F.
又∵AD=AE,∴DF=EF.
又∵BD=CE,
∴BD+DF=CE+EF,即BF=CF.
又∵AF⊥BC,
∴AB=AC.
8.解:相等.理由如下:
∵AB=AC,AD是高,∴BC=2BD.
∵AD,BE是高,∴∠ADC=∠AEH=∠BEC=90°.
∴∠HAE+∠C=90°,∠CBE+∠C=90°.
∴∠HAE=∠CBE.
在△AHE和△BCE中,
∴△AHE≌△BCE.∴AH=BC.
又∵BC=2BD,∴AH=2BD.
9.证明:∵AB=AC,AD是BC边上的中线,
∴AD⊥BC.∴∠ADB=90°.
又∵EF⊥AB,∴∠EFB=∠ADB=90°.
∵BG平分∠ABC,∴∠FBE=∠DBE.
又∵BE=BE,∴△FBE≌△DBE.
∴EF=ED.
10.证明:作∠BAC的平分线交BC于点E,
则∠EAC=∠BAC,∠AEC=90°.
∴∠EAC+∠C=90°.
∵BD⊥AC,垂足为D,
∴∠BDC=90°.
∴∠DBC+∠C=90°.
∴∠DBC=∠EAC=∠BAC.
11.证明:如,过点A作AF⊥BC于点F.
∵AB=AC,AF⊥BC,
∴∠BAF=∠CAF=∠BAC.
∵AD=AE,
∴∠D=∠AED=∠BAC.
∴∠BAF=∠D.
∴AF∥DE.
又∵AF⊥BC,
∴DE⊥BC.
12.解:∵AB=AC,∠1=∠ABC,∠2=∠ACB,
∴∠BOC=180°-(∠1+∠2)=180°-(∠ABC+∠ACB)=180°-(180°-∠A).
即∠BOC=90°+∠A.
∵∠1=∠ABC,∠2=∠ACB,
∴∠BOC=180°-(∠1+∠2)=180°-(∠ABC+∠ACB)=180°-(180°-∠A).
即∠BOC=120°+∠A.
∵∠1=∠ABC,∠2=∠ACB,
∴∠BOC=180°-(∠1+∠2)=180°-(∠ABC+∠ACB)=180°-(180°-∠A).
即∠BOC=+∠A.
等腰三角形的性质定理2:等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合(简记为:三线合一).
1.在△ABC中,AB=AC,点D在BC上.
(1)如果AD⊥BC,那么∠BAD=∠ ,BD= ;
(2)如果∠BAD=∠CAD,BC=6 cm,那么∠BDA= °,BD= cm;
(3)如果BD=CD,那么∠BAD=∠ ,AD⊥ .
2.[2020·房山期末] 如,在△ABC中,AB=AC,AD是△ABC的中线.若∠CAD=25°,则
∠B的度数是( )
A.25° B.55° C.65° D.75°
3.[2020·海淀期末] 如,在△ABC中,AB=AC,D是BC边上的动点(点D与点B,C不重合),△ABD和△ACD的面积分别表示为S1和S2,下列条件不能说明AD是△ABC角平分线的是( )
A.BD=CD
B.∠ADB=∠ADC
C.S1=S2
D.AD=BC
4.如,已知∠AOB,按照以下步骤作:
①以点O为圆心,以适当的长为半径作弧,分别交∠AOB的两边于点C,D,连接CD.
②分别以点C,D为圆心,以大于CD的长为半径作弧,两弧在∠AOB内交于点E,连接CE,DE.
③连接OE交CD于点M.
下列结论中错误的是( )
A.∠CEO=∠DEO B.CM=MD
C.∠OCD=∠ECD D.S四边形OCED=CD·OE
5.如是一个三角形测平架,已知AB=AC,在BC的中点D处挂一个铅锤E,让其自然下垂,调整架身,使点A恰好在铅垂线上,这时AD和BC的位置关系为 .
6.如所示,AB=AC,BD=CD,AD的延长线交BC于点E.求证:AE⊥BC.
7.[2020·大兴期末] 如,在△ABC中,点D,E在边BC上,BD=CE,且AD=AE.求证:AB=AC.
8.如,在△ABC中,AB=AC,AD和BE是高,它们相交于点H,且AE=BE,则AH与2BD相等吗 请说明理由.
9.如,在等腰三角形ABC中,AB=AC,AD是BC边上的中线,∠ABC的平分线BG交AD于点E,EF⊥AB,垂足为F.
求证:EF=ED.
10.如,已知AB=AC,BD⊥AC,垂足为D.求证:∠DBC=∠A.
11.如,在△ABC中,AB=AC,点D在BA的延长线上,点E在AC上,且AD=AE.求证:DE⊥BC.
12.在△ABC中,AB=AC,∠1=∠ABC,∠2=∠ACB,BD与CE相交于点O,如,∠BOC的大小与∠A的大小有什么关系
若∠1=∠ABC,∠2=∠ACB,则∠BOC与∠A的大小关系如何
若∠1=∠ABC,∠2=∠ACB,则∠BOC与∠A的大小关系如何
答案
1.(1)CAD CD (2)90 3 (3)CAD BC
等腰三角形三线合一的性质.
2.C
3.D
4.C
5.AD⊥BC
6.证明:在△BAD与△CAD中,
∴△BAD≌△CAD(SSS).
∴∠BAE=∠CAE.
又∵AB=AC,∴AE⊥BC.
7.证明:过点A作AF⊥BC于点F.
又∵AD=AE,∴DF=EF.
又∵BD=CE,
∴BD+DF=CE+EF,即BF=CF.
又∵AF⊥BC,
∴AB=AC.
8.解:相等.理由如下:
∵AB=AC,AD是高,∴BC=2BD.
∵AD,BE是高,∴∠ADC=∠AEH=∠BEC=90°.
∴∠HAE+∠C=90°,∠CBE+∠C=90°.
∴∠HAE=∠CBE.
在△AHE和△BCE中,
∴△AHE≌△BCE.∴AH=BC.
又∵BC=2BD,∴AH=2BD.
9.证明:∵AB=AC,AD是BC边上的中线,
∴AD⊥BC.∴∠ADB=90°.
又∵EF⊥AB,∴∠EFB=∠ADB=90°.
∵BG平分∠ABC,∴∠FBE=∠DBE.
又∵BE=BE,∴△FBE≌△DBE.
∴EF=ED.
10.证明:作∠BAC的平分线交BC于点E,
则∠EAC=∠BAC,∠AEC=90°.
∴∠EAC+∠C=90°.
∵BD⊥AC,垂足为D,
∴∠BDC=90°.
∴∠DBC+∠C=90°.
∴∠DBC=∠EAC=∠BAC.
11.证明:如,过点A作AF⊥BC于点F.
∵AB=AC,AF⊥BC,
∴∠BAF=∠CAF=∠BAC.
∵AD=AE,
∴∠D=∠AED=∠BAC.
∴∠BAF=∠D.
∴AF∥DE.
又∵AF⊥BC,
∴DE⊥BC.
12.解:∵AB=AC,∠1=∠ABC,∠2=∠ACB,
∴∠BOC=180°-(∠1+∠2)=180°-(∠ABC+∠ACB)=180°-(180°-∠A).
即∠BOC=90°+∠A.
∵∠1=∠ABC,∠2=∠ACB,
∴∠BOC=180°-(∠1+∠2)=180°-(∠ABC+∠ACB)=180°-(180°-∠A).
即∠BOC=120°+∠A.
∵∠1=∠ABC,∠2=∠ACB,
∴∠BOC=180°-(∠1+∠2)=180°-(∠ABC+∠ACB)=180°-(180°-∠A).
即∠BOC=+∠A.
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
