北京课改版数学八年级上册同步课时练习:12.8.4 作线段的垂直平分线(word版含答案)
文档属性
| 名称 | 北京课改版数学八年级上册同步课时练习:12.8.4 作线段的垂直平分线(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 250.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-17 00:00:00 | ||
图片预览

文档简介
12.8.4 作线段的垂直平分线
1.线段垂直平分线的作法(如):
(1)分别以A,B为圆心,大于AB的同样长为半径作弧,
两弧分别交于点C,D;
(2)作直线CD.
所以直线CD就是线段AB的垂直平分线.
2.线段垂直平分线的性质定理:线段垂直平分线上的点到线段两个端点的距离相等.
3.线段垂直平分线的判定定理:到线段两个端点距离相等的点在这条线段的垂直平分线上.
1.三角形纸片ABC上有一点P,量得PA=3 cm,PB=3 cm,则点P一定( )
A.是边AB的中点
B.在边AB的中线上
C.在边AB的高上
D.在边AB的垂直平分线上
2.到三角形三个顶点距离相等的点是( )
A.三条中线的交点
B.三条边垂直平分线的交点
C.三条角平分线的交点
D.三条高所在直线的交点
3.如,在△ABC中,AC的垂直平分线与AC,BC分别交于点E,D,EC=4,△ABC的周长为23,则△ABD的周长为( )
A.13 B.15 C.17 D.19
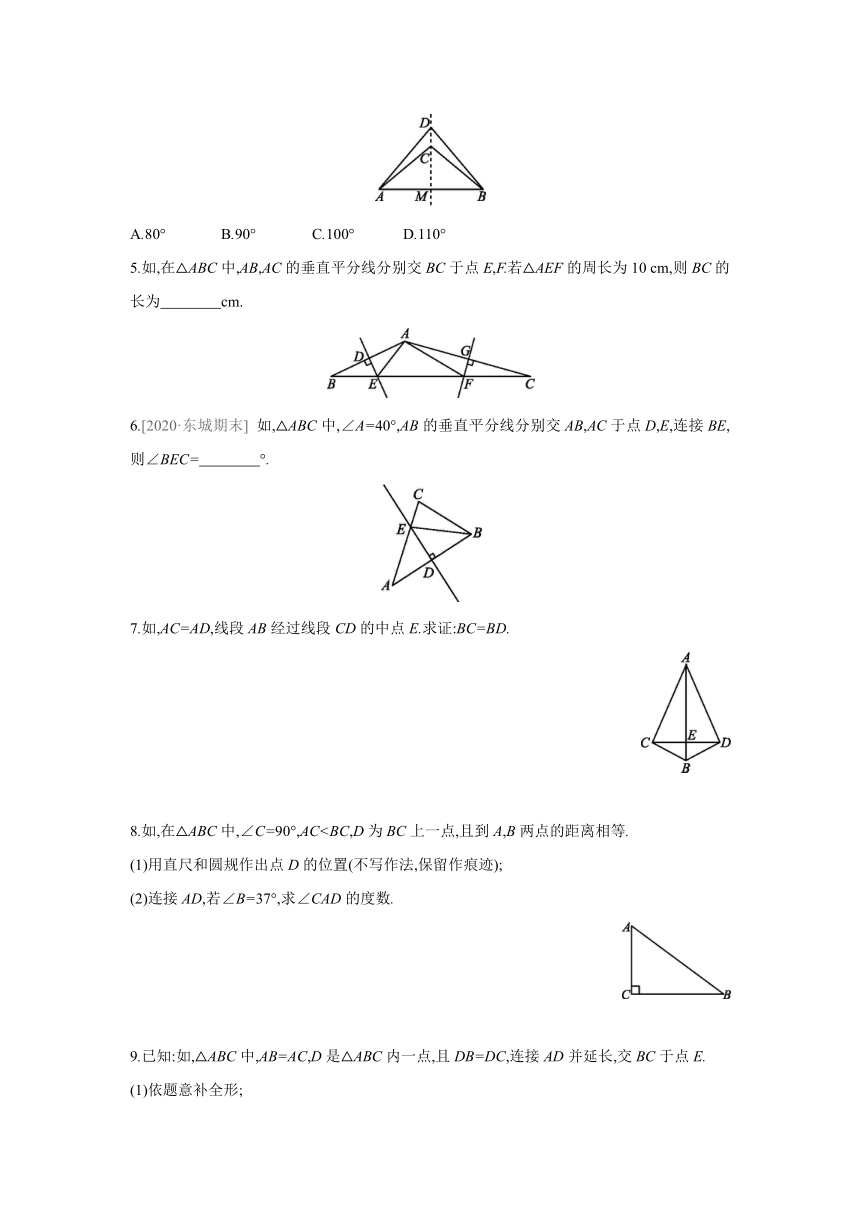
4.如,线段AB外有两点C,D(在AB同侧),若CA=CB,DA=DB,∠ADB=80°,∠CAD=10°,则∠ACB的度数为( )
A.80° B.90° C.100° D.110°
5.如,在△ABC中,AB,AC的垂直平分线分别交BC于点E,F.若△AEF的周长为10 cm,则BC的长为 cm.
6.[2020·东城期末] 如,△ABC中,∠A=40°,AB的垂直平分线分别交AB,AC于点D,E,连接BE,则∠BEC= °.
7.如,AC=AD,线段AB经过线段CD的中点E.求证:BC=BD.
8.如,在△ABC中,∠C=90°,AC(1)用直尺和圆规作出点D的位置(不写作法,保留作痕迹);
(2)连接AD,若∠B=37°,求∠CAD的度数.
9.已知:如,△ABC中,AB=AC,D是△ABC内一点,且DB=DC,连接AD并延长,交BC于点E.
(1)依题意补全形;
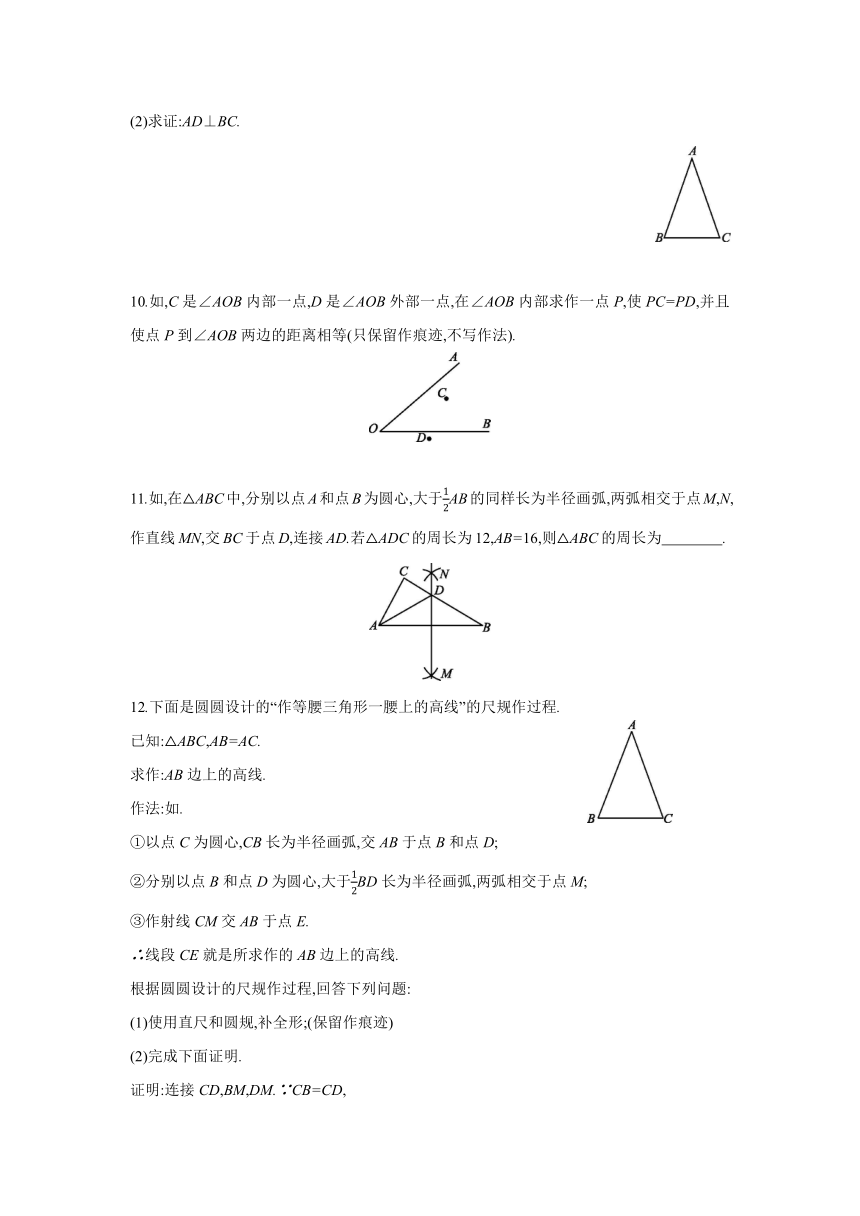
(2)求证:AD⊥BC.
10.如,C是∠AOB内部一点,D是∠AOB外部一点,在∠AOB内部求作一点P,使PC=PD,并且使点P到∠AOB两边的距离相等(只保留作痕迹,不写作法).
11.如,在△ABC中,分别以点A和点B为圆心,大于AB的同样长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为12,AB=16,则△ABC的周长为 .
12.下面是圆圆设计的“作等腰三角形一腰上的高线”的尺规作过程.
已知:△ABC,AB=AC.
求作:AB边上的高线.
作法:如.
①以点C为圆心,CB长为半径画弧,交AB于点B和点D;
②分别以点B和点D为圆心,大于BD长为半径画弧,两弧相交于点M;
③作射线CM交AB于点E.
∴线段CE就是所求作的AB边上的高线.
根据圆圆设计的尺规作过程,回答下列问题:
(1)使用直尺和圆规,补全形;(保留作痕迹)
(2)完成下面证明.
证明:连接CD,BM,DM.∵CB=CD,
∴点C在线段BD的垂直平分线上( )(填推理的依据).
∵ = ,
∴点M在线段BD的垂直平分线上.
∴CM是线段BD的垂直平分线.∴CM⊥BD.
∴线段CE就是AB边上的高线.
13.如所示,在△ABC中,∠ACB=90°,D是AB上一点,BD=BC,过点D作AB的垂线交AC于点E,CD交BE于点F.求证:BE垂直平分CD.
14.[2020·昌平期末] 在同一平面内,若点P与△ABC三个顶点中的任意两个顶点连接形成的三角形都是等腰三角形,则称P是△ABC的巧妙点.
(1)如①,求作△ABC的巧妙点P(尺规作,不写作法,保留作痕迹).
(2)如②,在△ABC中,∠A=80°,AB=AC,求作△ABC的所有巧妙点P(尺规作,不写作法,保留作痕迹),并直接写出∠BPC的度数是 .
(3)等边三角形的巧妙点的个数是( )
A.2 B.6 C.10 D.12
答案
1.D
2.B 根据垂直平分线的判定进行判断:到三角形三个顶点距离相等的点是三角形三条边垂直平分线的交点.
3.B ∵AC的垂直平分线与AC,BC分别交于E,D两点,∴AD=DC,AE=CE=4,即AC=8.∵△ABC的周长为23,∴AB+BC+AC=23.∴AB+BC=23-8=15.
∴△ABD的周长=AB+BD+AD=AB+BD+DC=AB+BC=15.
4.C ∵CA=CB,DA=DB,∴CD垂直平分AB且垂足为M.
∵∠ADB=80°,∠CAD=10°,
∴∠ACM=50°.∴∠ACB=100°.
5.10 ∵AB,AC的垂直平分线分别交BC于点E,F,∴AE=BE,AF=CF.
∴BC=BE+EF+CF=AE+EF+AF=10 cm.
6.80
7.证明:∵AC=AD,E是CD的中点,
∴AB垂直平分CD.
∴BC=BD.
8.解:(1)点D的位置如所示(D为AB的垂直平分线与BC的交点).
(2)如,∵在Rt△ABC中,∠B=37°,
∴∠CAB=53°.
∵AD=BD,∴∠BAD=∠B=37°.
∴∠CAD=∠CAB-∠BAD=53°-37°=16°.
9.解:(1)如所示:
(2)证明:∵AB=AC,DB=DC,
∴点A、点D都在线段BC的垂直平分线上.
∵两点确定一条直线,
∴直线AD是BC的垂直平分线.
∴AD⊥BC.
10.略
11.28 由题易知MN是AB的垂直平分线,
∴AD=BD.
∴AC+AD+CD=AC+BD+CD=AC+BC=12.
∴△ABC的周长为12+16=28.
12.解:(1)补全形如.
(2)到线段两个端点距离相等的点在这条线段的垂直平分线上 BM DM
13.证明:∵DE⊥AB,∠ACB=90°,
∴∠BDE=∠ACB=90°.
在Rt△BCE和Rt△BDE中,
∴Rt△BCE≌Rt△BDE(HL).
∴EC=ED.
∵BD=BC,EC=ED,
∴点B,E在线段CD的垂直平分线上.
∴BE垂直平分CD.
14.解:(1)如所示,点P即为所求.
(2)如所示,点P1,P2,P3,P4,P5,P6为所求.
∴从P1到P6的顺序,∠BPC的度数依次是40°,160°,140°,80°,40°,40°.
(3)C
1.线段垂直平分线的作法(如):
(1)分别以A,B为圆心,大于AB的同样长为半径作弧,
两弧分别交于点C,D;
(2)作直线CD.
所以直线CD就是线段AB的垂直平分线.
2.线段垂直平分线的性质定理:线段垂直平分线上的点到线段两个端点的距离相等.
3.线段垂直平分线的判定定理:到线段两个端点距离相等的点在这条线段的垂直平分线上.
1.三角形纸片ABC上有一点P,量得PA=3 cm,PB=3 cm,则点P一定( )
A.是边AB的中点
B.在边AB的中线上
C.在边AB的高上
D.在边AB的垂直平分线上
2.到三角形三个顶点距离相等的点是( )
A.三条中线的交点
B.三条边垂直平分线的交点
C.三条角平分线的交点
D.三条高所在直线的交点
3.如,在△ABC中,AC的垂直平分线与AC,BC分别交于点E,D,EC=4,△ABC的周长为23,则△ABD的周长为( )
A.13 B.15 C.17 D.19
4.如,线段AB外有两点C,D(在AB同侧),若CA=CB,DA=DB,∠ADB=80°,∠CAD=10°,则∠ACB的度数为( )
A.80° B.90° C.100° D.110°
5.如,在△ABC中,AB,AC的垂直平分线分别交BC于点E,F.若△AEF的周长为10 cm,则BC的长为 cm.
6.[2020·东城期末] 如,△ABC中,∠A=40°,AB的垂直平分线分别交AB,AC于点D,E,连接BE,则∠BEC= °.
7.如,AC=AD,线段AB经过线段CD的中点E.求证:BC=BD.
8.如,在△ABC中,∠C=90°,AC
(2)连接AD,若∠B=37°,求∠CAD的度数.
9.已知:如,△ABC中,AB=AC,D是△ABC内一点,且DB=DC,连接AD并延长,交BC于点E.
(1)依题意补全形;
(2)求证:AD⊥BC.
10.如,C是∠AOB内部一点,D是∠AOB外部一点,在∠AOB内部求作一点P,使PC=PD,并且使点P到∠AOB两边的距离相等(只保留作痕迹,不写作法).
11.如,在△ABC中,分别以点A和点B为圆心,大于AB的同样长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为12,AB=16,则△ABC的周长为 .
12.下面是圆圆设计的“作等腰三角形一腰上的高线”的尺规作过程.
已知:△ABC,AB=AC.
求作:AB边上的高线.
作法:如.
①以点C为圆心,CB长为半径画弧,交AB于点B和点D;
②分别以点B和点D为圆心,大于BD长为半径画弧,两弧相交于点M;
③作射线CM交AB于点E.
∴线段CE就是所求作的AB边上的高线.
根据圆圆设计的尺规作过程,回答下列问题:
(1)使用直尺和圆规,补全形;(保留作痕迹)
(2)完成下面证明.
证明:连接CD,BM,DM.∵CB=CD,
∴点C在线段BD的垂直平分线上( )(填推理的依据).
∵ = ,
∴点M在线段BD的垂直平分线上.
∴CM是线段BD的垂直平分线.∴CM⊥BD.
∴线段CE就是AB边上的高线.
13.如所示,在△ABC中,∠ACB=90°,D是AB上一点,BD=BC,过点D作AB的垂线交AC于点E,CD交BE于点F.求证:BE垂直平分CD.
14.[2020·昌平期末] 在同一平面内,若点P与△ABC三个顶点中的任意两个顶点连接形成的三角形都是等腰三角形,则称P是△ABC的巧妙点.
(1)如①,求作△ABC的巧妙点P(尺规作,不写作法,保留作痕迹).
(2)如②,在△ABC中,∠A=80°,AB=AC,求作△ABC的所有巧妙点P(尺规作,不写作法,保留作痕迹),并直接写出∠BPC的度数是 .
(3)等边三角形的巧妙点的个数是( )
A.2 B.6 C.10 D.12
答案
1.D
2.B 根据垂直平分线的判定进行判断:到三角形三个顶点距离相等的点是三角形三条边垂直平分线的交点.
3.B ∵AC的垂直平分线与AC,BC分别交于E,D两点,∴AD=DC,AE=CE=4,即AC=8.∵△ABC的周长为23,∴AB+BC+AC=23.∴AB+BC=23-8=15.
∴△ABD的周长=AB+BD+AD=AB+BD+DC=AB+BC=15.
4.C ∵CA=CB,DA=DB,∴CD垂直平分AB且垂足为M.
∵∠ADB=80°,∠CAD=10°,
∴∠ACM=50°.∴∠ACB=100°.
5.10 ∵AB,AC的垂直平分线分别交BC于点E,F,∴AE=BE,AF=CF.
∴BC=BE+EF+CF=AE+EF+AF=10 cm.
6.80
7.证明:∵AC=AD,E是CD的中点,
∴AB垂直平分CD.
∴BC=BD.
8.解:(1)点D的位置如所示(D为AB的垂直平分线与BC的交点).
(2)如,∵在Rt△ABC中,∠B=37°,
∴∠CAB=53°.
∵AD=BD,∴∠BAD=∠B=37°.
∴∠CAD=∠CAB-∠BAD=53°-37°=16°.
9.解:(1)如所示:
(2)证明:∵AB=AC,DB=DC,
∴点A、点D都在线段BC的垂直平分线上.
∵两点确定一条直线,
∴直线AD是BC的垂直平分线.
∴AD⊥BC.
10.略
11.28 由题易知MN是AB的垂直平分线,
∴AD=BD.
∴AC+AD+CD=AC+BD+CD=AC+BC=12.
∴△ABC的周长为12+16=28.
12.解:(1)补全形如.
(2)到线段两个端点距离相等的点在这条线段的垂直平分线上 BM DM
13.证明:∵DE⊥AB,∠ACB=90°,
∴∠BDE=∠ACB=90°.
在Rt△BCE和Rt△BDE中,
∴Rt△BCE≌Rt△BDE(HL).
∴EC=ED.
∵BD=BC,EC=ED,
∴点B,E在线段CD的垂直平分线上.
∴BE垂直平分CD.
14.解:(1)如所示,点P即为所求.
(2)如所示,点P1,P2,P3,P4,P5,P6为所求.
∴从P1到P6的顺序,∠BPC的度数依次是40°,160°,140°,80°,40°,40°.
(3)C
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
