北京课改版数学八年级上册同步课时练习:12.12 勾股定理的逆定理(word版含答案)
文档属性
| 名称 | 北京课改版数学八年级上册同步课时练习:12.12 勾股定理的逆定理(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 172.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-17 00:00:00 | ||
图片预览



文档简介
12.12 勾股定理的逆定理
勾股定理的逆定理:如果三角形的三边a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
1.以下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是( )
A.,, B.1,, C.6,7,8 D.2,3,4
2.在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,则下列条件中不能判定△ABC是直角三角形的是( )
A.b2=a2-c2
B.a2∶b2∶c2=1∶3∶2
C.∠C=∠A-∠B
D.∠A∶∠B∶∠C=3∶4∶5
3.已知一个直角三角形的两边长分别为3和4,则其第三边长的平方是( )
A.25 B.14 C.7 D.7或25
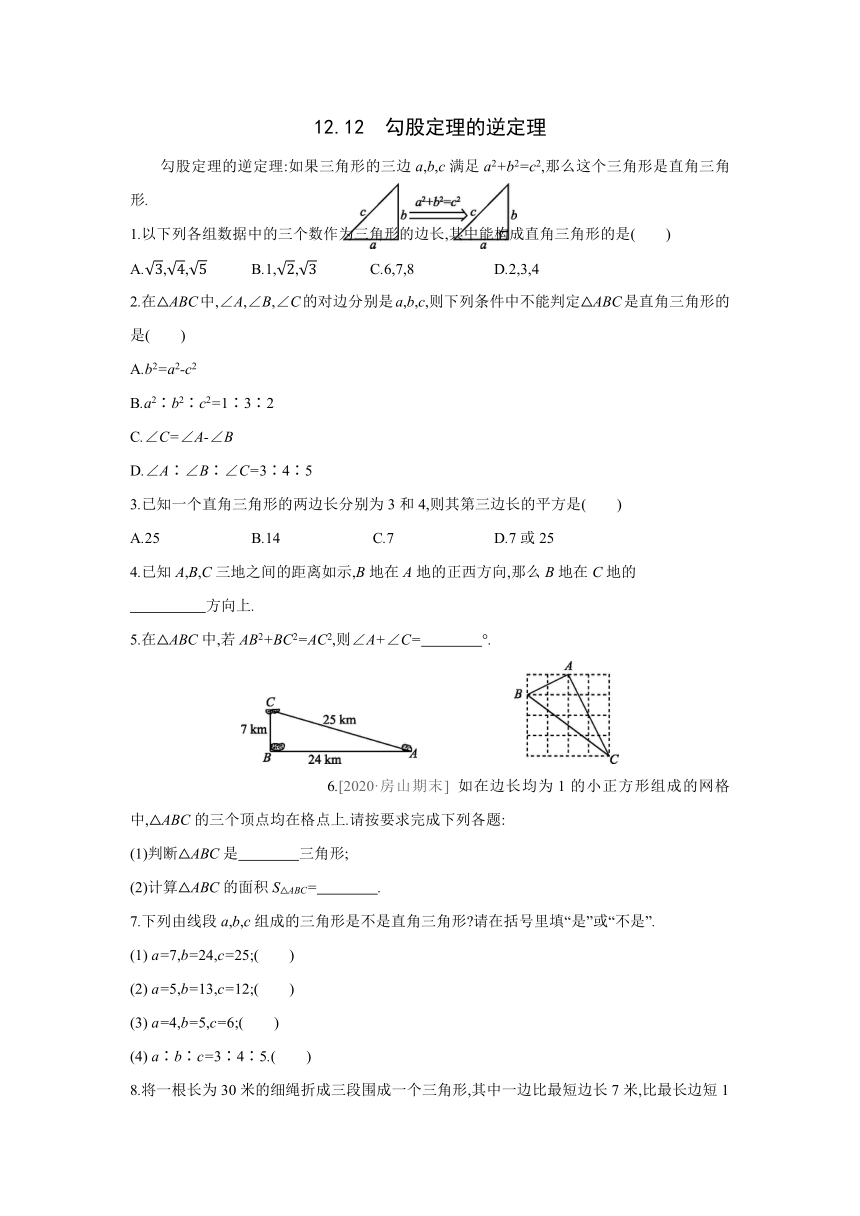
4.已知A,B,C三地之间的距离如示,B地在A地的正西方向,那么B地在C地的
方向上.
5.在△ABC中,若AB2+BC2=AC2,则∠A+∠C= °.
6.[2020·房山期末] 如在边长均为1的小正方形组成的网格中,△ABC的三个顶点均在格点上.请按要求完成下列各题:
(1)判断△ABC是 三角形;
(2)计算△ABC的面积S△ABC= .
7.下列由线段a,b,c组成的三角形是不是直角三角形 请在括号里填“是”或“不是”.
(1) a=7,b=24,c=25;( )
(2) a=5,b=13,c=12;( )
(3) a=4,b=5,c=6;( )
(4) a∶b∶c=3∶4∶5.( )
8.将一根长为30米的细绳折成三段围成一个三角形,其中一边比最短边长7米,比最长边短1米,试判断这个三角形的形状,并说明理由.
9.如在△ABC中,AB=13 cm,AC=24 cm,中线BD=5 cm.
求证:△ABC是等腰三角形.
10.已知△ABC的三边长分别是a,b,c,且满足a2+b2+c2+50=6a+8b+10c,试判断△ABC是不是直角三角形.
11.能够成为直角三角形三条边长的三个正整数,称为勾股数.对于任意两个正整数m,n(m>n),下列各组中的三个数为勾股数的一组是( )
A.m2+mn,m2-1,2mn
B.m2-n2,2mn,m2+n2
C.m+n,m-n,2mn
D.n2-1,n2+mn,2mn
12.如示,每个小方格都是边长为1的正方形,A,B是方格纸的两个格点(即正方形的顶点),在这个5×5的方格纸中,找出格点C,使△ABC是面积为1的直角三角形,这样的格点C有 个.
13.[2020·燕山期末] 如四边形ABCD中,∠B=90°,∠ACB=30°,AB=2,CD=3,AD=5.
(1)求证:AC⊥CD;
(2)求四边形ABCD的面积.
14.已知:如在△ABC中,CD是AB边上的高,且CD2=AD·BD.
求证:△ABC是直角三角形.
15.[2020·密云期末] 如△ABC中,AB的垂直平分线l交AB于点E,交AC于点D,AD=5,DC=3,BC=4.
(1)求证:△ABC是直角三角形;
(2)求AB的长.
16.如,点C,D把线段AB分割成AC,CD和DB三条线段,若以AC,CD,DB为边的三角形是一个直角三角形,则称点C,D是线段AB的勾股分割点.
(1)如果点M,N是线段AB的勾股分割点,且AM=3,MN=4,那么NB的长为 ;
(2)如②,点M,N在线段AB上,且AM∶MN∶NB=1∶1∶,CM=AM,NC=NB,则∠ACB的度数为 ;
(3)如③,点M,N是线段AB的勾股分割点,其中MN为最长线段,以AM,MN,NB为三边构造Rt△MCN,使CM=AM,NC=NB,连接AC,BC.依题意画出Rt△MCN,并直接写出∠ACB的度数.
答案
1.B
2.D A选项满足b2+c2=a2,B选项满足b2=a2+c2,因此都能判定△ABC是直角三角形;C选项可推出∠A=90°,能判定△ABC是直角三角形;由D选项求出的△ABC三个角的度数分别是45°,60°,75°,故它不是直角三角形.
3.D
4.正南 因为BC=7 km,AB=24 km,AC=25 km,72+242=252,所以BC2+AB2=AC2,
所以△ABC为直角三角形,即∠CBA=90°,
即B地在C地的正南方向上.
[点评] 求出∠CBA的度数后就可判断B地在C地的什么方向上.
5.90
6.(1)直角 (2)5
7.(1)是 (2)是 (3)不是 (4)是
(1)∵72 +242 =625,252 =625,
∴72 +242 =252.
∴这个三角形是直角三角形.
(2)∵52 +122 =169,132 =169,
∴52 +122 =132.
∴这个三角形是直角三角形.
(3)∵42 +52 =41,62 =36,
∴42 +52 ≠62.
∴这个三角形不是直角三角形.
(4)设三角形的三边长分别为3k,4k,5k(k>0).
∵(3k)2 + (4k)2 =25k2,(5k)2 =25k2,
∴(3k)2 +(4k)2=(5k)2.
∴这个三角形是直角三角形.
8.解:这个三角形是直角三角形.理由如下:
由题意:其中一边比最短边长7米,比最长边短1米,设此边长为x米,
则x+(x-7)+(x+1)=30,解得x=12.
则x-7=5,x+1=13,
所以三边长分别为5米、12米、13米.
因为52+122=169=132,
所以这个三角形是直角三角形.
9.证明:∵BD是△ABC的中线,
∴AD=CD=12 cm.
在△ABD中,AD2+BD2=122+52=169,
AB2=132=169,
∴AD2+BD2=AB2.∴∠ADB=90°.
即BD⊥AC.
∴BD垂直平分AC.
∴AB=BC.从而△ABC是等腰三角形.
10. 要判断△ABC是不是直角三角形,应先根据所给关系式求出a,b,c的值,再根据勾股定理的逆定理进行判断.
解:∵a2+b2+c2+50=6a+8b+10c,
∴(a2-6a+9)+(b2-8b+16)+(c2-10c+25)=0.
即(a-3)2+(b-4)2+(c-5)2=0.
∴a=3,b=4,c=5.
∵a2+b2=32+42=25,c2=52=25,
∴a2+b2=c2.
∴△ABC是直角三角形.
11.B 12.6
13.解:(1)证明:在Rt△ABC中,∠B=90°,∠ACB=30°,AB=2,
∴AC=2AB=4.
在△ACD中,AC=4,CD=3,AD=5,
∵42+32=52,
即AC2+CD2=AD2,
∴∠ACD=90°,
∴AC⊥CD.
(2)在Rt△ABC中,∠B=90°,AB=2,AC=4,
∴BC==2,
∴S△ABC=AB·BC=×2×2=2.
又∵S△ACD=AC·CD=×4×3=6,
∴四边形ABCD的面积为2+6.
14.证明:∵AC2=AD2+CD2,BC2=CD2+BD2,
∴AC2+BC2=AD2+2CD2+BD2=AD2+2AD·BD+BD2=(AD+BD)2=AB2.
∴△ABC是直角三角形.
15.解:(1)证明:连接BD.
∵AB的垂直平分线l交AC于点D,
∴AD=DB.
∵AD=5,∴BD=5.
在△DCB中,BD=5,CD=3,BC=4,
∴BD2=CD2+BC2,
∴∠BCD=90°,∴△ABC是直角三角形.
(2)在Rt△ACB中,
∵AB2=AC2+BC2=(3+5)2+42=80,
∴AB=4.
16. (1)∵MN>AM,
∴①若以MN为斜边,则有NB2+AM2=MN2,
∴NB=;
②若以AM,MN为直角边,则有MN2+AM2=NB2.
∴NB=5.
(2)∵AM∶MN∶NB=1∶1∶,
∴MN2+AM2=NB2.
即MN2+CM2=NC2.
∴∠CMN=90°.
∴∠MCN=∠CNM=45°.
∵CM=AM,NC=NB,
∴∠A=∠ACM=45°,∠B=∠NCB=22.5°.
∴∠ACB=∠ACM+∠MCN+∠NCB=112.5°.
(3)∵MN为最长线段,以AM,MN,NB为三边构造Rt△MCN,∴∠MCN=90°.
∴∠CMN+∠CNM=90°.
∵∠CMN=∠A+∠ACM,∠CNM=∠B+∠BCN,
∴∠A+∠ACM+∠B+∠BCN=90°.
∵AM=CM,CN=BN,
∴∠A=∠ACM,∠B=∠BCN.
∴2∠A+2∠B=90°.
∴∠A+∠B=45°.
∴∠ACB=135°.
解:(1)5或
(2)112.5°
(3)如,∠ACB=135°.
勾股定理的逆定理:如果三角形的三边a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
1.以下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是( )
A.,, B.1,, C.6,7,8 D.2,3,4
2.在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,则下列条件中不能判定△ABC是直角三角形的是( )
A.b2=a2-c2
B.a2∶b2∶c2=1∶3∶2
C.∠C=∠A-∠B
D.∠A∶∠B∶∠C=3∶4∶5
3.已知一个直角三角形的两边长分别为3和4,则其第三边长的平方是( )
A.25 B.14 C.7 D.7或25
4.已知A,B,C三地之间的距离如示,B地在A地的正西方向,那么B地在C地的
方向上.
5.在△ABC中,若AB2+BC2=AC2,则∠A+∠C= °.
6.[2020·房山期末] 如在边长均为1的小正方形组成的网格中,△ABC的三个顶点均在格点上.请按要求完成下列各题:
(1)判断△ABC是 三角形;
(2)计算△ABC的面积S△ABC= .
7.下列由线段a,b,c组成的三角形是不是直角三角形 请在括号里填“是”或“不是”.
(1) a=7,b=24,c=25;( )
(2) a=5,b=13,c=12;( )
(3) a=4,b=5,c=6;( )
(4) a∶b∶c=3∶4∶5.( )
8.将一根长为30米的细绳折成三段围成一个三角形,其中一边比最短边长7米,比最长边短1米,试判断这个三角形的形状,并说明理由.
9.如在△ABC中,AB=13 cm,AC=24 cm,中线BD=5 cm.
求证:△ABC是等腰三角形.
10.已知△ABC的三边长分别是a,b,c,且满足a2+b2+c2+50=6a+8b+10c,试判断△ABC是不是直角三角形.
11.能够成为直角三角形三条边长的三个正整数,称为勾股数.对于任意两个正整数m,n(m>n),下列各组中的三个数为勾股数的一组是( )
A.m2+mn,m2-1,2mn
B.m2-n2,2mn,m2+n2
C.m+n,m-n,2mn
D.n2-1,n2+mn,2mn
12.如示,每个小方格都是边长为1的正方形,A,B是方格纸的两个格点(即正方形的顶点),在这个5×5的方格纸中,找出格点C,使△ABC是面积为1的直角三角形,这样的格点C有 个.
13.[2020·燕山期末] 如四边形ABCD中,∠B=90°,∠ACB=30°,AB=2,CD=3,AD=5.
(1)求证:AC⊥CD;
(2)求四边形ABCD的面积.
14.已知:如在△ABC中,CD是AB边上的高,且CD2=AD·BD.
求证:△ABC是直角三角形.
15.[2020·密云期末] 如△ABC中,AB的垂直平分线l交AB于点E,交AC于点D,AD=5,DC=3,BC=4.
(1)求证:△ABC是直角三角形;
(2)求AB的长.
16.如,点C,D把线段AB分割成AC,CD和DB三条线段,若以AC,CD,DB为边的三角形是一个直角三角形,则称点C,D是线段AB的勾股分割点.
(1)如果点M,N是线段AB的勾股分割点,且AM=3,MN=4,那么NB的长为 ;
(2)如②,点M,N在线段AB上,且AM∶MN∶NB=1∶1∶,CM=AM,NC=NB,则∠ACB的度数为 ;
(3)如③,点M,N是线段AB的勾股分割点,其中MN为最长线段,以AM,MN,NB为三边构造Rt△MCN,使CM=AM,NC=NB,连接AC,BC.依题意画出Rt△MCN,并直接写出∠ACB的度数.
答案
1.B
2.D A选项满足b2+c2=a2,B选项满足b2=a2+c2,因此都能判定△ABC是直角三角形;C选项可推出∠A=90°,能判定△ABC是直角三角形;由D选项求出的△ABC三个角的度数分别是45°,60°,75°,故它不是直角三角形.
3.D
4.正南 因为BC=7 km,AB=24 km,AC=25 km,72+242=252,所以BC2+AB2=AC2,
所以△ABC为直角三角形,即∠CBA=90°,
即B地在C地的正南方向上.
[点评] 求出∠CBA的度数后就可判断B地在C地的什么方向上.
5.90
6.(1)直角 (2)5
7.(1)是 (2)是 (3)不是 (4)是
(1)∵72 +242 =625,252 =625,
∴72 +242 =252.
∴这个三角形是直角三角形.
(2)∵52 +122 =169,132 =169,
∴52 +122 =132.
∴这个三角形是直角三角形.
(3)∵42 +52 =41,62 =36,
∴42 +52 ≠62.
∴这个三角形不是直角三角形.
(4)设三角形的三边长分别为3k,4k,5k(k>0).
∵(3k)2 + (4k)2 =25k2,(5k)2 =25k2,
∴(3k)2 +(4k)2=(5k)2.
∴这个三角形是直角三角形.
8.解:这个三角形是直角三角形.理由如下:
由题意:其中一边比最短边长7米,比最长边短1米,设此边长为x米,
则x+(x-7)+(x+1)=30,解得x=12.
则x-7=5,x+1=13,
所以三边长分别为5米、12米、13米.
因为52+122=169=132,
所以这个三角形是直角三角形.
9.证明:∵BD是△ABC的中线,
∴AD=CD=12 cm.
在△ABD中,AD2+BD2=122+52=169,
AB2=132=169,
∴AD2+BD2=AB2.∴∠ADB=90°.
即BD⊥AC.
∴BD垂直平分AC.
∴AB=BC.从而△ABC是等腰三角形.
10. 要判断△ABC是不是直角三角形,应先根据所给关系式求出a,b,c的值,再根据勾股定理的逆定理进行判断.
解:∵a2+b2+c2+50=6a+8b+10c,
∴(a2-6a+9)+(b2-8b+16)+(c2-10c+25)=0.
即(a-3)2+(b-4)2+(c-5)2=0.
∴a=3,b=4,c=5.
∵a2+b2=32+42=25,c2=52=25,
∴a2+b2=c2.
∴△ABC是直角三角形.
11.B 12.6
13.解:(1)证明:在Rt△ABC中,∠B=90°,∠ACB=30°,AB=2,
∴AC=2AB=4.
在△ACD中,AC=4,CD=3,AD=5,
∵42+32=52,
即AC2+CD2=AD2,
∴∠ACD=90°,
∴AC⊥CD.
(2)在Rt△ABC中,∠B=90°,AB=2,AC=4,
∴BC==2,
∴S△ABC=AB·BC=×2×2=2.
又∵S△ACD=AC·CD=×4×3=6,
∴四边形ABCD的面积为2+6.
14.证明:∵AC2=AD2+CD2,BC2=CD2+BD2,
∴AC2+BC2=AD2+2CD2+BD2=AD2+2AD·BD+BD2=(AD+BD)2=AB2.
∴△ABC是直角三角形.
15.解:(1)证明:连接BD.
∵AB的垂直平分线l交AC于点D,
∴AD=DB.
∵AD=5,∴BD=5.
在△DCB中,BD=5,CD=3,BC=4,
∴BD2=CD2+BC2,
∴∠BCD=90°,∴△ABC是直角三角形.
(2)在Rt△ACB中,
∵AB2=AC2+BC2=(3+5)2+42=80,
∴AB=4.
16. (1)∵MN>AM,
∴①若以MN为斜边,则有NB2+AM2=MN2,
∴NB=;
②若以AM,MN为直角边,则有MN2+AM2=NB2.
∴NB=5.
(2)∵AM∶MN∶NB=1∶1∶,
∴MN2+AM2=NB2.
即MN2+CM2=NC2.
∴∠CMN=90°.
∴∠MCN=∠CNM=45°.
∵CM=AM,NC=NB,
∴∠A=∠ACM=45°,∠B=∠NCB=22.5°.
∴∠ACB=∠ACM+∠MCN+∠NCB=112.5°.
(3)∵MN为最长线段,以AM,MN,NB为三边构造Rt△MCN,∴∠MCN=90°.
∴∠CMN+∠CNM=90°.
∵∠CMN=∠A+∠ACM,∠CNM=∠B+∠BCN,
∴∠A+∠ACM+∠B+∠BCN=90°.
∵AM=CM,CN=BN,
∴∠A=∠ACM,∠B=∠BCN.
∴2∠A+2∠B=90°.
∴∠A+∠B=45°.
∴∠ACB=135°.
解:(1)5或
(2)112.5°
(3)如,∠ACB=135°.
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
