北京课改版数学八年级上册同步课时练习:12.11 勾股定理(word版含答案)
文档属性
| 名称 | 北京课改版数学八年级上册同步课时练习:12.11 勾股定理(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 213.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-17 00:00:00 | ||
图片预览


文档简介
12.11 勾股定理
勾股定理:在直角三角形中,两直角边的平方和等于斜边的平方.
即a2+b2=c2(如.
1.已知Rt△ABC的三条边长分别是a,b,c,则下列各式成立的是( )
A.a+b=c B.a+b>c
C.a+b2.某校的长方形操场,如果一学生要从A处走到C处,那么他至少要走( )
A.140米 B.120米 C.100米 D.90米
3.如点A表示的实数是( )
A. B. C.- D.-
4.如在△ABC中,∠C=90°,AC=2,点D在BC上,∠ADC=2∠B,AD=,则BC的长为( )
A.-1 B.+1 C.-1 D.+1
5.[2019·毕节] 如点E在正方形ABCD的边AB上,若EB=1,EC=2,则正方形ABCD的面积为( )
A. B.3 C. D.5
6.如果将长为6 cm,宽为5 cm的长方形纸片折叠一次,那么这条折痕的长不可能是( )
A.8 cm B.5 cm C.5.5 cm D.1 cm
7.[2020·顺义期末] 用四个全等的直角三角形拼成如个大正方形ABCD和一个小正方形EFGH,这就是著名的“赵爽弦”.在2002年北京召开的国际数学家大会就用这个弦作为会标.若AB=10,AF=8,则小正方形EFGH的面积为 .
8.[2020·大兴期末] 已知直角三角形的两边长分别为3 cm,4 cm,则第三边长为 .
9.已知A,B,C三地的位置如示,∠C=90°,A,C两地相距4 km,B,C两地相距3 km,则A,B两地间的距离是 km;若A地在C地的正东方向,则B地在C地的 方向.
10.如示,在等腰直角三角形ABC中, ∠C=90°, 则AC∶BC∶AB= .
11.已知等腰三角形的一条腰长为5,底边长是6,则底边上的高为 .
12.如已知△ABC中,∠ACB=90°,AB=15,AC=12,以直角边BC为直径作半圆,则这个半圆的面积是 .
13.将两个完全相同的长方形拼成如所示的形,长方形的长为a,宽为b,对角线长为c,连接AF,请你利用直角梯形EFAC的面积的不同表示方法来验证勾股定理.
14.如,一张三角形纸片ABC,∠C=90°,AC=8 cm,BC=6 cm,现将纸片折叠,使点A与点B重合,那么折痕长等于 cm.
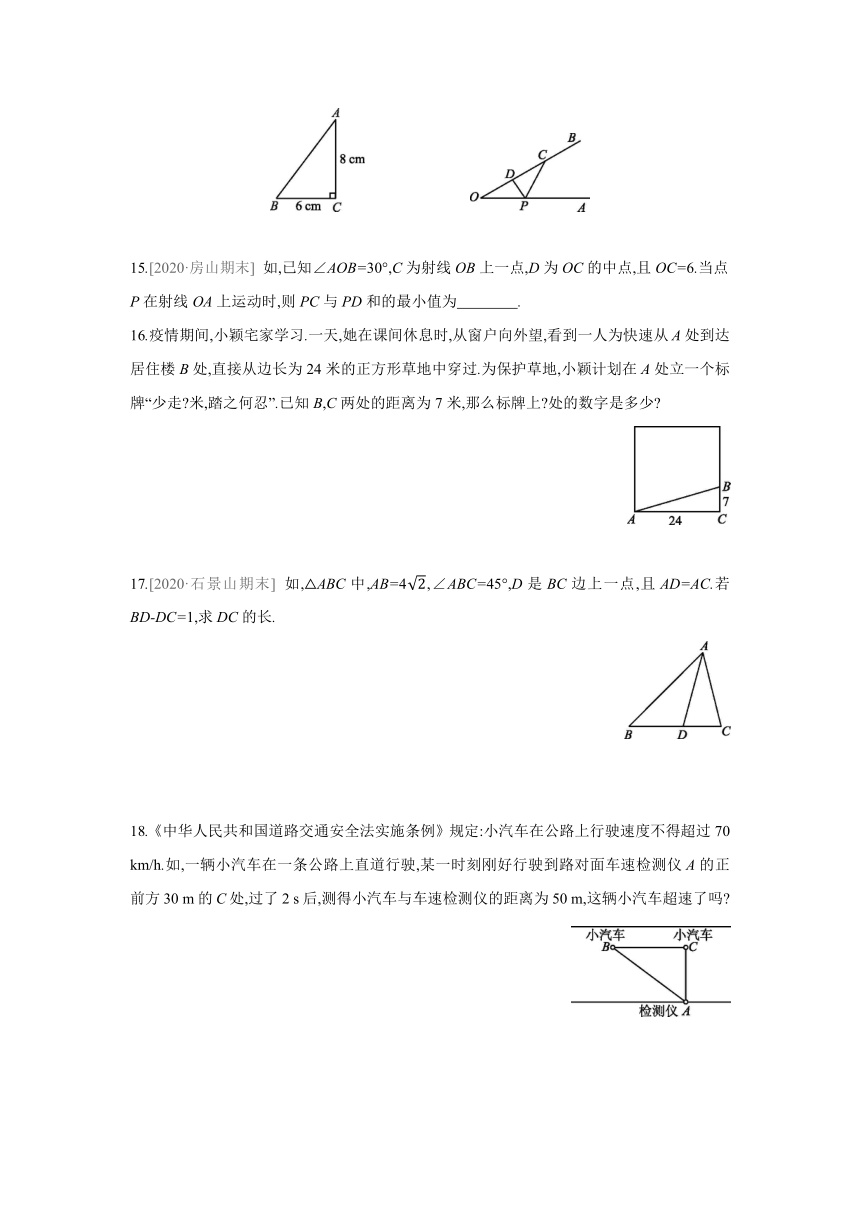
15.[2020·房山期末] 如,已知∠AOB=30°,C为射线OB上一点,D为OC的中点,且OC=6.当点P在射线OA上运动时,则PC与PD和的最小值为 .
16.疫情期间,小颖宅家学习.一天,她在课间休息时,从窗户向外望,看到一人为快速从A处到达居住楼B处,直接从边长为24米的正方形草地中穿过.为保护草地,小颖计划在A处立一个标牌“少走 米,踏之何忍”.已知B,C两处的距离为7米,那么标牌上 处的数字是多少
17.[2020·石景山期末] 如,△ABC中,AB=4,∠ABC=45°,D是BC边上一点,且AD=AC.若BD-DC=1,求DC的长.
18.《中华人民共和国道路交通安全法实施条例》规定:小汽车在公路上行驶速度不得超过70 km/h.如,一辆小汽车在一条公路上直道行驶,某一时刻刚好行驶到路对面车速检测仪A的正前方30 m的C处,过了2 s后,测得小汽车与车速检测仪的距离为50 m,这辆小汽车超速了吗
答案
1.B
2.C 连接AC,根据勾股定理可得至少要走100米.故选C.
3.C 如,根据勾股定理可得OC===,所以OA=.又因为点A在数轴的负半轴上,所以点A表示的实数是-.故选C.
4.D ∵∠C=90°,
∴DC===1.
∵∠ADC=∠B+∠BAD,∠ADC=2∠B,
∴∠B=∠BAD.
∴BD=AD=.
∴BC=+1.
故选D.
5.B 6.A 7.4
8.5 cm或 cm
9.5 正北
10.1∶1∶ 设AC=BC=a,
则AB===a.
故AC∶BC∶AB=1∶1∶.
11.4 如所示,由等腰三角形“三线合一”的性质知BD=DC=3.
在Rt△ABD中,AB=5,由勾股定理,得AB2=AD2+BD2,所以AD2=AB2-BD2,所以AD==
=4.
12.10.125π 由勾股定理得BC===9,所以以直角边BC=9为直径的半圆面积为10.125π.
13.解:由题意知梯形EFAC是直角梯形,△ABF是等腰直角三角形.
梯形EFAC的面积有以下两种求法:
①梯形EFAC的面积=×(上底+下底)×高=(a+b)(a+b)=(a+b)2;
②梯形EFAC的面积是△ABF,△ABC与△BEF的面积之和,即c2+ab+ab=ab+c2.
所以(a+b)2=ab+c2,整理得a2+b2=c2.
14. 如,在Rt△ABC中,因为AC=8 cm,BC=6 cm,根据勾股定理,得AB=10 cm.设CE=x cm,由折叠的性质得BD=AD=5 cm, BE=AE=(8-x)cm.在Rt△BCE中,根据勾股定理可知BC2+CE2=BE2,即62+x2=(8-x)2,解方程得x=.所以BE=8-=(cm).
在Rt△BDE中,根据勾股定理可知DE===(cm).
15.3
16.解:由题意可知AB===25(米),
故居民从A处直接到B处要走AB=25米.
若居民不践踏草地应走AC+BC=24+7=31(米),
∴AC+BC-AB=31-25=6(米).
故标牌上 处的数字为6.
17.解:如,过点A作AE⊥BC于点E.
∵AD=AC,
∴∠AEB=90°,DE=EC.
又∠ABC=45°,∴∠BAE=45°.
∴AE=BE.
在Rt△ABE中,AB=4,
∴AE2+BE2=AB2,
即BE2+BE2=(4)2,
∴BE=4,即BD+DC=4.
又∵BD-DC=1,
∴DC=2.
18.解:由题意得在Rt△ABC中,AC=30 m,AB=50 m.
根据勾股定理可得BC===40(m),
∴小汽车的速度v==20(m/s)=72 km/h.
∵72 km/h>70 km/h,
∴这辆小汽车超速了.
勾股定理:在直角三角形中,两直角边的平方和等于斜边的平方.
即a2+b2=c2(如.
1.已知Rt△ABC的三条边长分别是a,b,c,则下列各式成立的是( )
A.a+b=c B.a+b>c
C.a+b
A.140米 B.120米 C.100米 D.90米
3.如点A表示的实数是( )
A. B. C.- D.-
4.如在△ABC中,∠C=90°,AC=2,点D在BC上,∠ADC=2∠B,AD=,则BC的长为( )
A.-1 B.+1 C.-1 D.+1
5.[2019·毕节] 如点E在正方形ABCD的边AB上,若EB=1,EC=2,则正方形ABCD的面积为( )
A. B.3 C. D.5
6.如果将长为6 cm,宽为5 cm的长方形纸片折叠一次,那么这条折痕的长不可能是( )
A.8 cm B.5 cm C.5.5 cm D.1 cm
7.[2020·顺义期末] 用四个全等的直角三角形拼成如个大正方形ABCD和一个小正方形EFGH,这就是著名的“赵爽弦”.在2002年北京召开的国际数学家大会就用这个弦作为会标.若AB=10,AF=8,则小正方形EFGH的面积为 .
8.[2020·大兴期末] 已知直角三角形的两边长分别为3 cm,4 cm,则第三边长为 .
9.已知A,B,C三地的位置如示,∠C=90°,A,C两地相距4 km,B,C两地相距3 km,则A,B两地间的距离是 km;若A地在C地的正东方向,则B地在C地的 方向.
10.如示,在等腰直角三角形ABC中, ∠C=90°, 则AC∶BC∶AB= .
11.已知等腰三角形的一条腰长为5,底边长是6,则底边上的高为 .
12.如已知△ABC中,∠ACB=90°,AB=15,AC=12,以直角边BC为直径作半圆,则这个半圆的面积是 .
13.将两个完全相同的长方形拼成如所示的形,长方形的长为a,宽为b,对角线长为c,连接AF,请你利用直角梯形EFAC的面积的不同表示方法来验证勾股定理.
14.如,一张三角形纸片ABC,∠C=90°,AC=8 cm,BC=6 cm,现将纸片折叠,使点A与点B重合,那么折痕长等于 cm.
15.[2020·房山期末] 如,已知∠AOB=30°,C为射线OB上一点,D为OC的中点,且OC=6.当点P在射线OA上运动时,则PC与PD和的最小值为 .
16.疫情期间,小颖宅家学习.一天,她在课间休息时,从窗户向外望,看到一人为快速从A处到达居住楼B处,直接从边长为24米的正方形草地中穿过.为保护草地,小颖计划在A处立一个标牌“少走 米,踏之何忍”.已知B,C两处的距离为7米,那么标牌上 处的数字是多少
17.[2020·石景山期末] 如,△ABC中,AB=4,∠ABC=45°,D是BC边上一点,且AD=AC.若BD-DC=1,求DC的长.
18.《中华人民共和国道路交通安全法实施条例》规定:小汽车在公路上行驶速度不得超过70 km/h.如,一辆小汽车在一条公路上直道行驶,某一时刻刚好行驶到路对面车速检测仪A的正前方30 m的C处,过了2 s后,测得小汽车与车速检测仪的距离为50 m,这辆小汽车超速了吗
答案
1.B
2.C 连接AC,根据勾股定理可得至少要走100米.故选C.
3.C 如,根据勾股定理可得OC===,所以OA=.又因为点A在数轴的负半轴上,所以点A表示的实数是-.故选C.
4.D ∵∠C=90°,
∴DC===1.
∵∠ADC=∠B+∠BAD,∠ADC=2∠B,
∴∠B=∠BAD.
∴BD=AD=.
∴BC=+1.
故选D.
5.B 6.A 7.4
8.5 cm或 cm
9.5 正北
10.1∶1∶ 设AC=BC=a,
则AB===a.
故AC∶BC∶AB=1∶1∶.
11.4 如所示,由等腰三角形“三线合一”的性质知BD=DC=3.
在Rt△ABD中,AB=5,由勾股定理,得AB2=AD2+BD2,所以AD2=AB2-BD2,所以AD==
=4.
12.10.125π 由勾股定理得BC===9,所以以直角边BC=9为直径的半圆面积为10.125π.
13.解:由题意知梯形EFAC是直角梯形,△ABF是等腰直角三角形.
梯形EFAC的面积有以下两种求法:
①梯形EFAC的面积=×(上底+下底)×高=(a+b)(a+b)=(a+b)2;
②梯形EFAC的面积是△ABF,△ABC与△BEF的面积之和,即c2+ab+ab=ab+c2.
所以(a+b)2=ab+c2,整理得a2+b2=c2.
14. 如,在Rt△ABC中,因为AC=8 cm,BC=6 cm,根据勾股定理,得AB=10 cm.设CE=x cm,由折叠的性质得BD=AD=5 cm, BE=AE=(8-x)cm.在Rt△BCE中,根据勾股定理可知BC2+CE2=BE2,即62+x2=(8-x)2,解方程得x=.所以BE=8-=(cm).
在Rt△BDE中,根据勾股定理可知DE===(cm).
15.3
16.解:由题意可知AB===25(米),
故居民从A处直接到B处要走AB=25米.
若居民不践踏草地应走AC+BC=24+7=31(米),
∴AC+BC-AB=31-25=6(米).
故标牌上 处的数字为6.
17.解:如,过点A作AE⊥BC于点E.
∵AD=AC,
∴∠AEB=90°,DE=EC.
又∠ABC=45°,∴∠BAE=45°.
∴AE=BE.
在Rt△ABE中,AB=4,
∴AE2+BE2=AB2,
即BE2+BE2=(4)2,
∴BE=4,即BD+DC=4.
又∵BD-DC=1,
∴DC=2.
18.解:由题意得在Rt△ABC中,AC=30 m,AB=50 m.
根据勾股定理可得BC===40(m),
∴小汽车的速度v==20(m/s)=72 km/h.
∵72 km/h>70 km/h,
∴这辆小汽车超速了.
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
