北京课改版数学九年级上册同步课时练习:18.5.1 相似三角形的判定(一)(word版含答案)
文档属性
| 名称 | 北京课改版数学九年级上册同步课时练习:18.5.1 相似三角形的判定(一)(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 195.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-17 00:00:00 | ||
图片预览



文档简介
18.5 第1课时 相似三角形的判定(一)
平行于三角形一边的直线,截其他两边所得的三角形与原三角形相似.
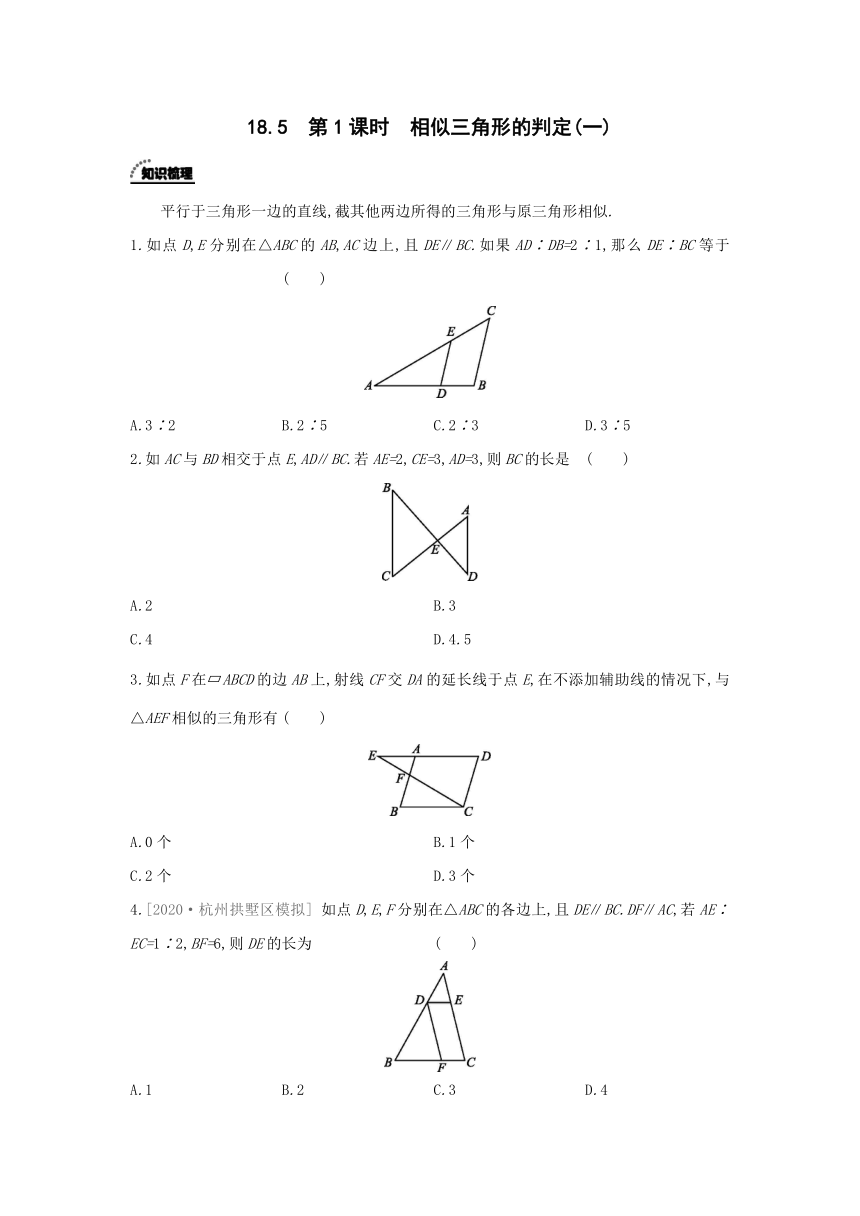
1.如点D,E分别在△ABC的AB,AC边上,且DE∥BC.如果AD∶DB=2∶1,那么DE∶BC等于 ( )
A.3∶2 B.2∶5 C.2∶3 D.3∶5
2.如AC与BD相交于点E,AD∥BC.若AE=2,CE=3,AD=3,则BC的长是 ( )
A.2 B.3
C.4 D.4.5
3.如点F在 ABCD的边AB上,射线CF交DA的延长线于点E,在不添加辅助线的情况下,与△AEF相似的三角形有 ( )
A.0个 B.1个
C.2个 D.3个
4.[2020·杭州拱墅区模拟] 如点D,E,F分别在△ABC的各边上,且DE∥BC.DF∥AC,若AE∶EC=1∶2,BF=6,则DE的长为 ( )
A.1 B.2 C.3 D.4
5.[2019·西城区期末] 如在△ABC中,点D,E分别在AB,AC上,且DE∥BC.若AD=2,AB=3,DE=4,则BC的长为 .
6.如DE∥BC交BA的延长线于点D,交CA的延长线于点E,AD=4,DE∶BC=1∶2,则AB= .
7.在物理课中,同学们曾学过小孔成像:在较暗的屋子里,把一支点燃的蜡烛放在一块半透明的塑料薄膜前面,在它们之间放一块钻有小孔的纸板,由于光沿直线传播,塑料薄膜上就出现了蜡烛火焰倒立的像,这种现象就是小孔成像(如).如②(示意),如果火焰AB的高度是2 cm,倒立的像A'B'的高度为5 cm,蜡烛火焰根B到小孔O的距离为4 cm,则火焰根的像B'到小孔O的距离是 cm.
8.已知:如AB∥MN,BC∥NG.
求证:=.
9.如AB∥CD,AD与BC相交于点P,AB=4,CD=7,AD=10.求AP的长.
10.如,四边形ABCD是平行四边形,AE平分∠BAD,交DC的延长线于点E,交BC于点F,AB=3,EF=0.8,AF=2.4.求AD的长.
11.已知:如,四边形BDFE是菱形,DC=EF,且DC=2.求AE的长.
12.如,AD⊥BC于点D,点E在边AB上,CE与AD交于点G,EF⊥AD于点F,AE=5 cm,BE=10 cm,BD=9 cm,CD=5 cm,求AF,FG,GD的长.
13.已知:在Rt△ABC中,∠C=90°,D是AB边上一点.过点D作一条与△ABC任一边平行的直线截原三角形成小三角形,并使它和原三角形相似.如果AB=10,AC∶BC=3∶4,AD=6,请求出DE的长.(注:E是过点D所作的直线与△ABC另一边的交点)
答案
1.C 2.D 3.C 4.C
5.6 6.8
7.10 解: 由题可知△ABO∽△A'B'O,
∴=,∴=,∴B'O=10 cm.
8.证明:∵AB∥MN,
∴△OAB∽△OMN,
∴=.
同理,得=,∴=.
9.解:∵AB∥CD,∴△APB∽△DPC,
∴AB∶DC=AP∶DP=AP∶(AD-AP),
即4∶7=AP∶(10-AP),∴AP=.
10.解:∵四边形ABCD为平行四边形,
∴DC=AB=3,AB∥DE,
∴△AFB∽△EFC,∴=.
∵AB=3,EF=0.8,AF=2.4,
∴=,∴EC=1,
∴DE=DC+EC=3+1=4.
∵AB∥DE,∴∠BAE=∠E.
∵AE平分∠BAD,∴∠BAE=∠DAE,
∴∠E=∠DAE,则AD=DE=4.
∴AD的长为4.
11.解:∵DC=EF,且DC=2,∴EF=4.
∵四边形BDFE是菱形,
∴BD=BE=EF=4,EF∥BC,
∴BC=BD+DC=6.
∵EF∥BC,∴△AEF∽△ABC,
∴===,
即=,∴AE=8.
12.解:∵AD⊥BC,EF⊥AD,∴EF∥BC,
∴△AEF∽△ABD,∴=.
∵AE=5 cm,BE=10 cm,
∴AB=15 cm.
又∵BD=9 cm,
在Rt△ABD中,可得AD=12 cm.
则=,∴AF=4 cm.
∵EF∥BC,
∴△EFG∽△CDG,
∴=.
在Rt△AEF中,∵AE=5 cm,AF=4 cm,
∴EF=3 cm,∴=.
又∵FD=AD-AF=8 cm,
∴FG=3 cm,GD=5 cm.
13.解: “构造平行,出现相似”是今后解决相似问题的重点.
解:依题意,得AB=10,AC=6,BC=8,BD=4,符合题意的小三角形可以作出两个.
情况一:如①,过点D作DE∥AC交BC于点E,
∴△BDE∽△BAC,
∴=,
∴DE=·AC=×6=2.4.
情况二:如②,过点D作DE∥BC交AC于点E,
∴△ADE∽△ABC,
∴=,
∴DE=·BC=×8=4.8.
综上可知,DE的长为2.4或4.8.
平行于三角形一边的直线,截其他两边所得的三角形与原三角形相似.
1.如点D,E分别在△ABC的AB,AC边上,且DE∥BC.如果AD∶DB=2∶1,那么DE∶BC等于 ( )
A.3∶2 B.2∶5 C.2∶3 D.3∶5
2.如AC与BD相交于点E,AD∥BC.若AE=2,CE=3,AD=3,则BC的长是 ( )
A.2 B.3
C.4 D.4.5
3.如点F在 ABCD的边AB上,射线CF交DA的延长线于点E,在不添加辅助线的情况下,与△AEF相似的三角形有 ( )
A.0个 B.1个
C.2个 D.3个
4.[2020·杭州拱墅区模拟] 如点D,E,F分别在△ABC的各边上,且DE∥BC.DF∥AC,若AE∶EC=1∶2,BF=6,则DE的长为 ( )
A.1 B.2 C.3 D.4
5.[2019·西城区期末] 如在△ABC中,点D,E分别在AB,AC上,且DE∥BC.若AD=2,AB=3,DE=4,则BC的长为 .
6.如DE∥BC交BA的延长线于点D,交CA的延长线于点E,AD=4,DE∶BC=1∶2,则AB= .
7.在物理课中,同学们曾学过小孔成像:在较暗的屋子里,把一支点燃的蜡烛放在一块半透明的塑料薄膜前面,在它们之间放一块钻有小孔的纸板,由于光沿直线传播,塑料薄膜上就出现了蜡烛火焰倒立的像,这种现象就是小孔成像(如).如②(示意),如果火焰AB的高度是2 cm,倒立的像A'B'的高度为5 cm,蜡烛火焰根B到小孔O的距离为4 cm,则火焰根的像B'到小孔O的距离是 cm.
8.已知:如AB∥MN,BC∥NG.
求证:=.
9.如AB∥CD,AD与BC相交于点P,AB=4,CD=7,AD=10.求AP的长.
10.如,四边形ABCD是平行四边形,AE平分∠BAD,交DC的延长线于点E,交BC于点F,AB=3,EF=0.8,AF=2.4.求AD的长.
11.已知:如,四边形BDFE是菱形,DC=EF,且DC=2.求AE的长.
12.如,AD⊥BC于点D,点E在边AB上,CE与AD交于点G,EF⊥AD于点F,AE=5 cm,BE=10 cm,BD=9 cm,CD=5 cm,求AF,FG,GD的长.
13.已知:在Rt△ABC中,∠C=90°,D是AB边上一点.过点D作一条与△ABC任一边平行的直线截原三角形成小三角形,并使它和原三角形相似.如果AB=10,AC∶BC=3∶4,AD=6,请求出DE的长.(注:E是过点D所作的直线与△ABC另一边的交点)
答案
1.C 2.D 3.C 4.C
5.6 6.8
7.10 解: 由题可知△ABO∽△A'B'O,
∴=,∴=,∴B'O=10 cm.
8.证明:∵AB∥MN,
∴△OAB∽△OMN,
∴=.
同理,得=,∴=.
9.解:∵AB∥CD,∴△APB∽△DPC,
∴AB∶DC=AP∶DP=AP∶(AD-AP),
即4∶7=AP∶(10-AP),∴AP=.
10.解:∵四边形ABCD为平行四边形,
∴DC=AB=3,AB∥DE,
∴△AFB∽△EFC,∴=.
∵AB=3,EF=0.8,AF=2.4,
∴=,∴EC=1,
∴DE=DC+EC=3+1=4.
∵AB∥DE,∴∠BAE=∠E.
∵AE平分∠BAD,∴∠BAE=∠DAE,
∴∠E=∠DAE,则AD=DE=4.
∴AD的长为4.
11.解:∵DC=EF,且DC=2,∴EF=4.
∵四边形BDFE是菱形,
∴BD=BE=EF=4,EF∥BC,
∴BC=BD+DC=6.
∵EF∥BC,∴△AEF∽△ABC,
∴===,
即=,∴AE=8.
12.解:∵AD⊥BC,EF⊥AD,∴EF∥BC,
∴△AEF∽△ABD,∴=.
∵AE=5 cm,BE=10 cm,
∴AB=15 cm.
又∵BD=9 cm,
在Rt△ABD中,可得AD=12 cm.
则=,∴AF=4 cm.
∵EF∥BC,
∴△EFG∽△CDG,
∴=.
在Rt△AEF中,∵AE=5 cm,AF=4 cm,
∴EF=3 cm,∴=.
又∵FD=AD-AF=8 cm,
∴FG=3 cm,GD=5 cm.
13.解: “构造平行,出现相似”是今后解决相似问题的重点.
解:依题意,得AB=10,AC=6,BC=8,BD=4,符合题意的小三角形可以作出两个.
情况一:如①,过点D作DE∥AC交BC于点E,
∴△BDE∽△BAC,
∴=,
∴DE=·AC=×6=2.4.
情况二:如②,过点D作DE∥BC交AC于点E,
∴△ADE∽△ABC,
∴=,
∴DE=·BC=×8=4.8.
综上可知,DE的长为2.4或4.8.
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
