北京课改版数学九年级下册同步课时练习:第二十五章 概率的求法与应用 单元测试(word版含答案)
文档属性
| 名称 | 北京课改版数学九年级下册同步课时练习:第二十五章 概率的求法与应用 单元测试(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 154.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-17 16:07:41 | ||
图片预览


文档简介
第二十五章 概率的求法与应用 单元测试
一、选择题(每题4分,共28分)
1.现有2个60°的角、1个90°的角与1个120°的角,则从中任意取出两个角,取出的两个角恰好互补的概率是 ( )
A. B. C. D.
2.下列说法正确的是 ( )
A.一枚质地均匀的骰子已连续抛掷了2000次,其中抛掷出5点的次数最少,则第2001次一定抛掷出5点
B.抛掷一枚钉,钉尖触地和钉尖朝上的概率不相等
C.明天降雨的概率是80%,表示明天有80%的时间降雨
D.某种彩票中奖的概率是1%,因此买100张该种彩票一定会中奖
3.下列事件中,发生的概率是的事件是 ( )
A.抛一枚质地均匀的正方体骰子,出现偶数点
B.在26个英文字母中,随机抽取一个,为元音字母
C.在1,2,3,4,5,6六个数字中,随机抽取一个能被6整除
D.在1,2,3,4,5,6六个数字中,随机抽取一个能被3整除
4.某校安排三辆车,组织九年级学生团员去敬老院参加学雷锋活动,其中小王与小菲都可以从这三辆车中任选一辆搭乘,则小王与小菲同车的概率为( )
A. B. C. D.
5.向如示的正三角形区域扔沙包(区域中每一个小正三角形除颜色不同外其余完全相同).假设沙包击中每一个小正三角形是等可能的,则扔沙包一次,击中阴影区域的概率为 ( )
A. B. C. D.
6.一个均匀的立方体六个面上分别标有数字1,2,3,4,5,6.这个立方体的平面展开,抛掷这个立方体,则朝上一面上的数恰好等于朝下一面的数的的概率是( )
A. B. C. D.
7.一个不透明的盒子里有n个除颜色外其他完全相同的小球,其中有9个黄球.每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色后再放回盒子,通过大量摸球实验后发现,摸到黄球的频率稳定在30%,那么估计盒子中小球的个数n为( )
A.20 B.24 C.28 D.30
二、填空题(每题5分,共20分)
8.一个不透明的盒子中装有4个黄球、3个红球和1个绿球,这些球除了颜色外无其他差别.从中随机摸出一个球,恰好是红球的概率是 .
9.某毛绒玩具厂对一批毛绒玩具进行质量抽检,相关数据如下:
抽取的毛绒 玩具数n 20 50 100 200 500 1000 1500 2000
优等品的 频数m 19 47 91 184 462 921 1379 1846
优等品的 频率 0.950 0.940 0.910 0.920 0.924 0.921 0.919 0.923
从这批玩具中,任意抽取的一个毛绒玩具是优等品的概率的估计值是 .(精确到0.01)
10.如示,A,B是边长为1的小正方形组成的网格中的两个格点,在格点上任意选择点C,恰好能组成一个△ABC,且面积为1的概率是 .
11.在-1,1,2这三个数中任选2个数分别作为点P的横坐标和纵坐标,过点P画双曲线y=,该双曲线位于第一、三象限的概率是 .
三、解答题(共52分)
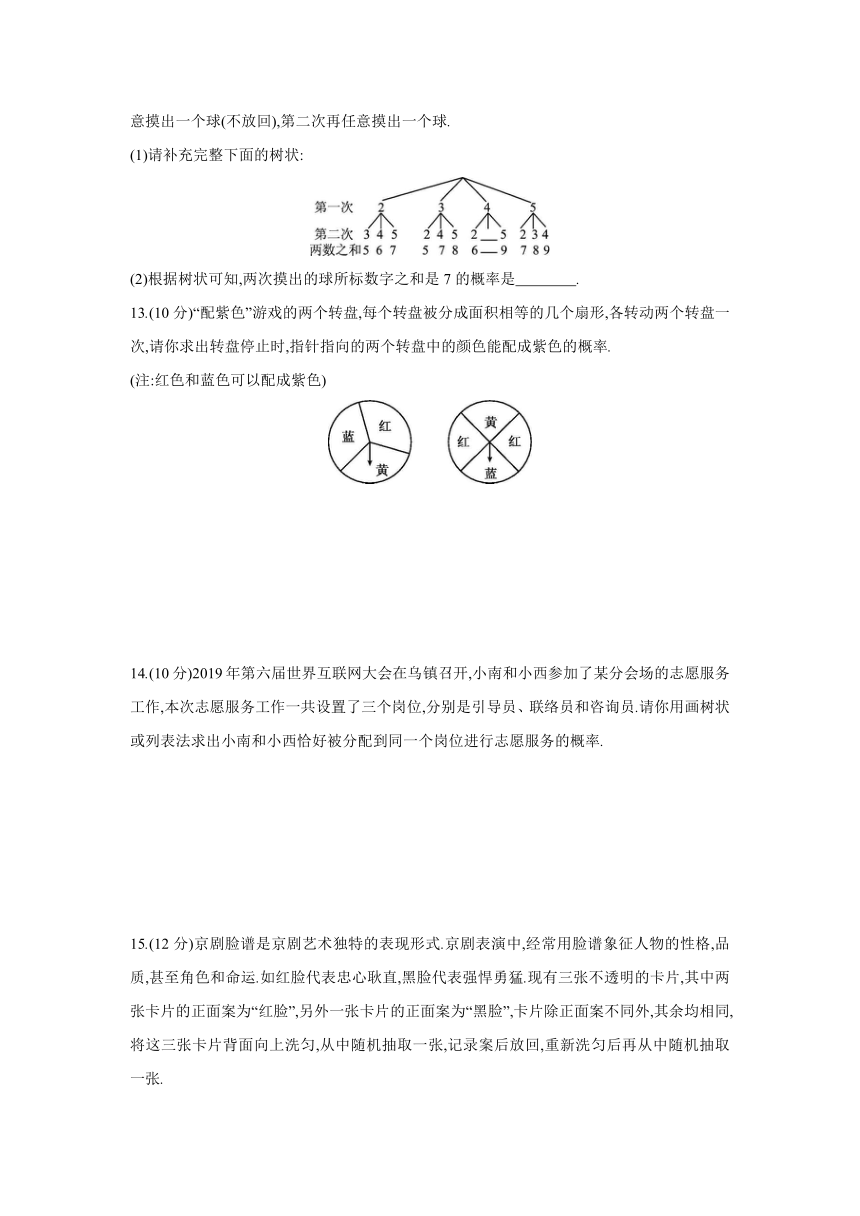
12.(8分)把4个完全相同的乒乓球标上数字2,3,4,5,然后放到一个不透明的口袋中,第一次任意摸出一个球(不放回),第二次再任意摸出一个球.
(1)请补充完整下面的树状:
(2)根据树状可知,两次摸出的球所标数字之和是7的概率是 .
13.(10分)“配紫色”游戏的两个转盘,每个转盘被分成面积相等的几个扇形,各转动两个转盘一次,请你求出转盘停止时,指针指向的两个转盘中的颜色能配成紫色的概率.
(注:红色和蓝色可以配成紫色)
14.(10分)2019年第六届世界互联网大会在乌镇召开,小南和小西参加了某分会场的志愿服务工作,本次志愿服务工作一共设置了三个岗位,分别是引导员、联络员和咨询员.请你用画树状或列表法求出小南和小西恰好被分配到同一个岗位进行志愿服务的概率.
15.(12分)京剧脸谱是京剧艺术独特的表现形式.京剧表演中,经常用脸谱象征人物的性格,品质,甚至角色和命运.如红脸代表忠心耿直,黑脸代表强悍勇猛.现有三张不透明的卡片,其中两张卡片的正面案为“红脸”,另外一张卡片的正面案为“黑脸”,卡片除正面案不同外,其余均相同,将这三张卡片背面向上洗匀,从中随机抽取一张,记录案后放回,重新洗匀后再从中随机抽取一张.
请用画树状或列表的方法,求抽出的两张卡片上的案都是“红脸”的概率.(案为“红脸”的两张卡片分别记为A1,A2,案为“黑脸”的卡片记为B)
16.(12分)甲、乙两人进行摸牌游戏.现有十张形状、大小完全相同的牌,正面分别标有数字1~10.从中选出一些牌,将这些牌背面朝上,洗匀后放在桌子上.甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.若两人抽取的数字和为2的倍数,则甲获胜;其余情况乙获胜.
(1)若选出三张分别标有数字2,3,5的牌,这个游戏公平吗 请利用画树状法或列表法来说明理由.
(2)乙说:“若我在2,3,5三张牌外再选一张牌,共四张牌进行游戏,则我可以让自己获胜的可能性比甲大”,请判断乙的说法是否正确.若正确,请写出乙再选哪些牌可以让自己获胜的可能性比甲大;若不正确,请说明理由.
答案
1.B 2.B 3.D 4.A
5.C 解: 求出中阴影部分的面积占整个形面积的比即可.击中阴影区域的概率为=.
6.A
7.D 解: 由题意可知×100%≈30%,解得n≈30.故选D.
8. 9.0.92
10. 解: 此格点中共有36个格点,要想能组成△ABC且面积为1,那么符合要求的格点如所示.
从上可知,符合要求的点共有8个,所以恰好能组成一个△ABC且面积为1的概率是.
11. 12. (1)3 7 (2)
13.解:画树状如所示:
由树状可知,共有12种等可能的情况,其中能配成紫色的有3种,故P(配成紫色)=.
14.解:分别用字母A,B,C代替引导员、联络员和咨询员岗位,记小南和小西恰好被分配到同一个岗位进行志愿服务为事件M.
用列表法列举所有可能出现的结果如下:
小南 小西 A B C
A AA AB AC
B BA BB BC
C CA CB CC
由表中可以看出,所有等可能的结果有9种,满足事件M的结果有3种,即AA,BB,CC,
∴P(M)==.
15.解:画树状如下:
由树状可知,所有等可能出现的结果共有9种,其中两次抽取的卡片上都是“红脸”的结果有4种,所以P(两张都是“红脸”)=.
16.解:(1)这个游戏不公平.
理由:画树状如下:
从中看出,共有9种结果,每种结果出现的可能性相同,其中两人抽取的数字和为2的倍数的结果有5种,
所以甲获胜的概率为,乙获胜的概率是,因此这个游戏不公平.
(2)不正确.
理由如下:当选择的牌是奇数时,P(甲获胜)=,P(乙获胜)=;
当选择的牌是偶数时,P(甲获胜)=,P(乙获胜)=.
因此,乙不可以让自己获胜的可能性比甲大.
一、选择题(每题4分,共28分)
1.现有2个60°的角、1个90°的角与1个120°的角,则从中任意取出两个角,取出的两个角恰好互补的概率是 ( )
A. B. C. D.
2.下列说法正确的是 ( )
A.一枚质地均匀的骰子已连续抛掷了2000次,其中抛掷出5点的次数最少,则第2001次一定抛掷出5点
B.抛掷一枚钉,钉尖触地和钉尖朝上的概率不相等
C.明天降雨的概率是80%,表示明天有80%的时间降雨
D.某种彩票中奖的概率是1%,因此买100张该种彩票一定会中奖
3.下列事件中,发生的概率是的事件是 ( )
A.抛一枚质地均匀的正方体骰子,出现偶数点
B.在26个英文字母中,随机抽取一个,为元音字母
C.在1,2,3,4,5,6六个数字中,随机抽取一个能被6整除
D.在1,2,3,4,5,6六个数字中,随机抽取一个能被3整除
4.某校安排三辆车,组织九年级学生团员去敬老院参加学雷锋活动,其中小王与小菲都可以从这三辆车中任选一辆搭乘,则小王与小菲同车的概率为( )
A. B. C. D.
5.向如示的正三角形区域扔沙包(区域中每一个小正三角形除颜色不同外其余完全相同).假设沙包击中每一个小正三角形是等可能的,则扔沙包一次,击中阴影区域的概率为 ( )
A. B. C. D.
6.一个均匀的立方体六个面上分别标有数字1,2,3,4,5,6.这个立方体的平面展开,抛掷这个立方体,则朝上一面上的数恰好等于朝下一面的数的的概率是( )
A. B. C. D.
7.一个不透明的盒子里有n个除颜色外其他完全相同的小球,其中有9个黄球.每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色后再放回盒子,通过大量摸球实验后发现,摸到黄球的频率稳定在30%,那么估计盒子中小球的个数n为( )
A.20 B.24 C.28 D.30
二、填空题(每题5分,共20分)
8.一个不透明的盒子中装有4个黄球、3个红球和1个绿球,这些球除了颜色外无其他差别.从中随机摸出一个球,恰好是红球的概率是 .
9.某毛绒玩具厂对一批毛绒玩具进行质量抽检,相关数据如下:
抽取的毛绒 玩具数n 20 50 100 200 500 1000 1500 2000
优等品的 频数m 19 47 91 184 462 921 1379 1846
优等品的 频率 0.950 0.940 0.910 0.920 0.924 0.921 0.919 0.923
从这批玩具中,任意抽取的一个毛绒玩具是优等品的概率的估计值是 .(精确到0.01)
10.如示,A,B是边长为1的小正方形组成的网格中的两个格点,在格点上任意选择点C,恰好能组成一个△ABC,且面积为1的概率是 .
11.在-1,1,2这三个数中任选2个数分别作为点P的横坐标和纵坐标,过点P画双曲线y=,该双曲线位于第一、三象限的概率是 .
三、解答题(共52分)
12.(8分)把4个完全相同的乒乓球标上数字2,3,4,5,然后放到一个不透明的口袋中,第一次任意摸出一个球(不放回),第二次再任意摸出一个球.
(1)请补充完整下面的树状:
(2)根据树状可知,两次摸出的球所标数字之和是7的概率是 .
13.(10分)“配紫色”游戏的两个转盘,每个转盘被分成面积相等的几个扇形,各转动两个转盘一次,请你求出转盘停止时,指针指向的两个转盘中的颜色能配成紫色的概率.
(注:红色和蓝色可以配成紫色)
14.(10分)2019年第六届世界互联网大会在乌镇召开,小南和小西参加了某分会场的志愿服务工作,本次志愿服务工作一共设置了三个岗位,分别是引导员、联络员和咨询员.请你用画树状或列表法求出小南和小西恰好被分配到同一个岗位进行志愿服务的概率.
15.(12分)京剧脸谱是京剧艺术独特的表现形式.京剧表演中,经常用脸谱象征人物的性格,品质,甚至角色和命运.如红脸代表忠心耿直,黑脸代表强悍勇猛.现有三张不透明的卡片,其中两张卡片的正面案为“红脸”,另外一张卡片的正面案为“黑脸”,卡片除正面案不同外,其余均相同,将这三张卡片背面向上洗匀,从中随机抽取一张,记录案后放回,重新洗匀后再从中随机抽取一张.
请用画树状或列表的方法,求抽出的两张卡片上的案都是“红脸”的概率.(案为“红脸”的两张卡片分别记为A1,A2,案为“黑脸”的卡片记为B)
16.(12分)甲、乙两人进行摸牌游戏.现有十张形状、大小完全相同的牌,正面分别标有数字1~10.从中选出一些牌,将这些牌背面朝上,洗匀后放在桌子上.甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.若两人抽取的数字和为2的倍数,则甲获胜;其余情况乙获胜.
(1)若选出三张分别标有数字2,3,5的牌,这个游戏公平吗 请利用画树状法或列表法来说明理由.
(2)乙说:“若我在2,3,5三张牌外再选一张牌,共四张牌进行游戏,则我可以让自己获胜的可能性比甲大”,请判断乙的说法是否正确.若正确,请写出乙再选哪些牌可以让自己获胜的可能性比甲大;若不正确,请说明理由.
答案
1.B 2.B 3.D 4.A
5.C 解: 求出中阴影部分的面积占整个形面积的比即可.击中阴影区域的概率为=.
6.A
7.D 解: 由题意可知×100%≈30%,解得n≈30.故选D.
8. 9.0.92
10. 解: 此格点中共有36个格点,要想能组成△ABC且面积为1,那么符合要求的格点如所示.
从上可知,符合要求的点共有8个,所以恰好能组成一个△ABC且面积为1的概率是.
11. 12. (1)3 7 (2)
13.解:画树状如所示:
由树状可知,共有12种等可能的情况,其中能配成紫色的有3种,故P(配成紫色)=.
14.解:分别用字母A,B,C代替引导员、联络员和咨询员岗位,记小南和小西恰好被分配到同一个岗位进行志愿服务为事件M.
用列表法列举所有可能出现的结果如下:
小南 小西 A B C
A AA AB AC
B BA BB BC
C CA CB CC
由表中可以看出,所有等可能的结果有9种,满足事件M的结果有3种,即AA,BB,CC,
∴P(M)==.
15.解:画树状如下:
由树状可知,所有等可能出现的结果共有9种,其中两次抽取的卡片上都是“红脸”的结果有4种,所以P(两张都是“红脸”)=.
16.解:(1)这个游戏不公平.
理由:画树状如下:
从中看出,共有9种结果,每种结果出现的可能性相同,其中两人抽取的数字和为2的倍数的结果有5种,
所以甲获胜的概率为,乙获胜的概率是,因此这个游戏不公平.
(2)不正确.
理由如下:当选择的牌是奇数时,P(甲获胜)=,P(乙获胜)=;
当选择的牌是偶数时,P(甲获胜)=,P(乙获胜)=.
因此,乙不可以让自己获胜的可能性比甲大.
