北京课改版数学九年级上册同步课时练习:18.5 第4课时 相似三角形的判定 (word版含答案)
文档属性
| 名称 | 北京课改版数学九年级上册同步课时练习:18.5 第4课时 相似三角形的判定 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 182.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-18 06:34:39 | ||
图片预览



文档简介
18.5 第4课时 相似三角形的判定(四)
1.如,AD是Rt△ABC斜边上的中线,AE⊥AD交CB的延长线于点E,则中一定相似的三角形是 ( )
A.△AED与△ACB
B.△AEB与△ACD
C.△BAE与△ACE
D.△AEC与△DAC
2.如,AB∥CD,AD,BC相交于点O,E,F分别是OA,OB的中点.若OB=4,OC=3,EF=4,则CD的长为 ( )
A. B.4 C.6 D.8
3.如,点D,E分别在△ABC的AB,AC边上,增加下列条件中的一个:①∠AED=∠B;②∠ADE=∠C;③=;④=;⑤AC2=AD·AE,能使△ADE与△ACB一定相似的有 ( )
A.①②④ B.②④⑤
C.①②③④ D.①②③⑤
4.如,等边三角形ABC的边长为3,P为BC边上一点,且BP=1,D为AC边上一点.若∠APD=60°,则CD的长为 ( )
A. B. C. D.1
5.如,在△ABC中,∠ACB=90°,CD是斜边AB上的高,AD=9,BD=4,那么CD= ,AC= .
6.[2020·海淀区期末] 如,在△ABC与△ADE中,=,且∠EAC=∠DAB.
求证:△ABC∽△ADE.
7.如,已知∠ACB=∠CBD=90°,AC=4 cm,BC=3 cm,那么BD为多少时,△ACB与△CBD相似
8.[2020·西城区期末] 如,在△ABC中,AD平分∠BAC,E是AD上一点,且BE=BD.
(1)求证:△ABE∽△ACD;
(2)若BD=1,CD=2,求的值.
9.如,在 ABCD中,E是AB延长线上一点,连接DE,交AC于点G,交BC于点F,请找出中所有相似的三角形(不含全等三角形),任选其中一对进行证明.
10.如,在△ABC中,AB=8 cm,BC=16 cm,点P从点A出发沿AB边向点B以2 cm/s的速度移动,点Q从点B出发沿BC边向点C以4 cm/s的速度移动,如果点P,Q分别从点A,B同时出发,当点Q到达点C时,两点同时停止运动.经过几秒△BPQ和△BAC相似
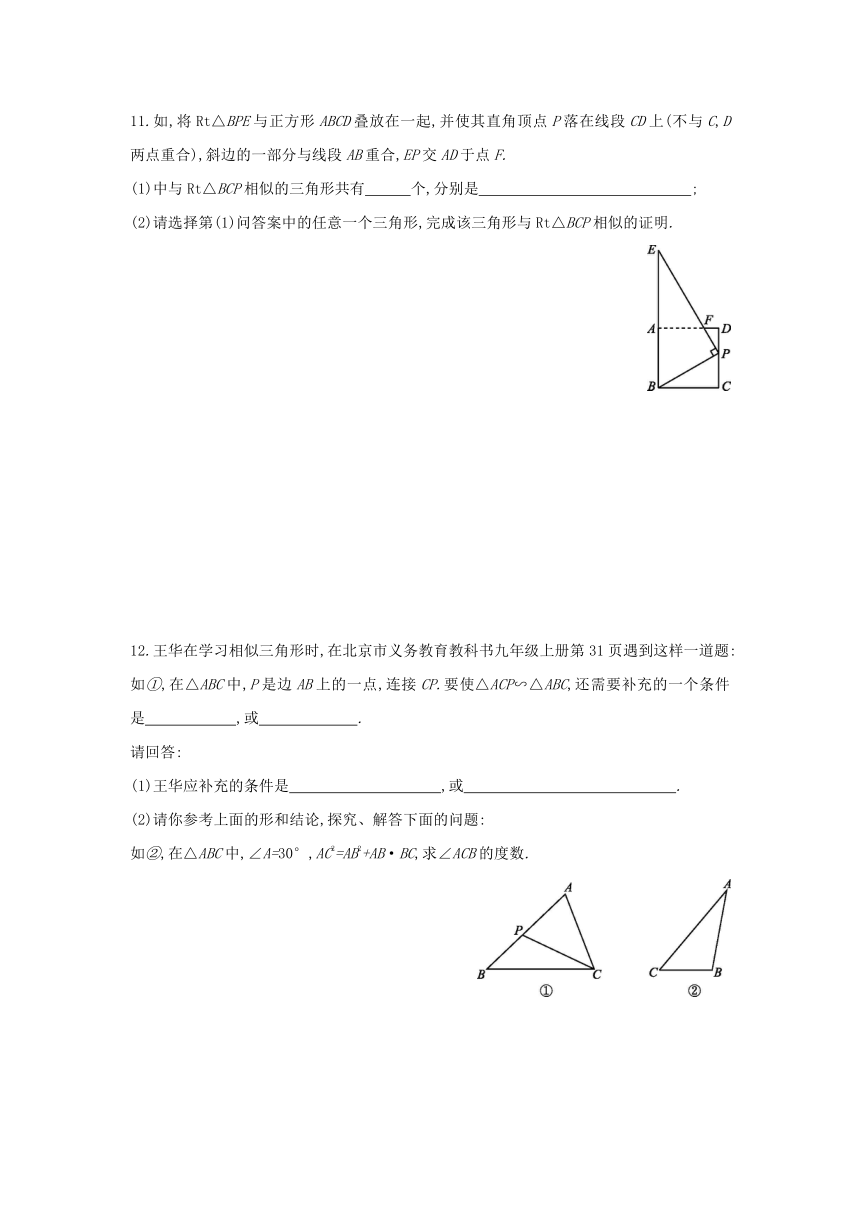
11.如,将Rt△BPE与正方形ABCD叠放在一起,并使其直角顶点P落在线段CD上(不与C,D两点重合),斜边的一部分与线段AB重合,EP交AD于点F.
(1)中与Rt△BCP相似的三角形共有 个,分别是 ;
(2)请选择第(1)问答案中的任意一个三角形,完成该三角形与Rt△BCP相似的证明.
12.王华在学习相似三角形时,在北京市义务教育教科书九年级上册第31页遇到这样一道题:如①,在△ABC中,P是边AB上的一点,连接CP.要使△ACP∽△ABC,还需要补充的一个条件是 ,或 .
请回答:
(1)王华应补充的条件是 ,或 .
(2)请你参考上面的形和结论,探究、解答下面的问题:
如②,在△ABC中,∠A=30°,AC2=AB2+AB·BC,求∠ACB的度数.
答案
1.C 解: ∵AD是Rt△ABC斜边上的中线,
∴AD=BD=CD,
∴∠C=∠DAC.
∵∠BAE+∠BAD=90°,∠DAC+∠BAD=90°,
∴∠BAE=∠DAC,∴∠C=∠BAE.
又∵∠E=∠E,∴△BAE∽△ACE.
2.C 3.A 4.B 5.6 3
6.证明:∵∠EAC=∠DAB,
∴∠EAC+∠BAE=∠DAB+∠BAE,
∴∠BAC=∠DAE.
又∵=,∴△ABC∽△ADE.
7.解: 此类问题,不能想当然地认为就是△ACB∽△CBD,等角的不同决定了相似三角形对应点的不同,一定要注意分类讨论.
解:∵∠ACB=∠CBD=90°,
∴分以下两种情况讨论.
当△ACB∽△DBC时,
==1,∴DB=AC=4 cm;
当△ACB∽△CBD时,
=,∴DB==(cm).
综上所述,当BD为4 cm或 cm时,△ACB与△CBD相似.
[点评] 中考对数学思想的考查是非常到位的,分类讨论的数学思想是中考考查的重点.
8.解:(1)证明:∵AD平分∠BAC,
∴∠BAE=∠CAD.
∵BE=BD,∴∠BED=∠BDE,
∴∠AEB=∠ADC,
∴△ABE∽△ACD.
(2)∵△ABE∽△ACD,
∴=.
∵BE=BD=1,CD=2,
∴=.
9.解:△EFB∽△EDA,△FGC∽△DGA,△EBF∽△DCF,△GAE∽△GCD,△ADE∽△CFD.
选择△EFB∽△EDA进行证明.
证明:∵四边形ABCD是平行四边形,
∴BC∥AD,
∴△EFB∽△EDA.(所选相似三角形不唯一)
10.解:设经过t s△BPQ和△BAC相似.
当△BPQ∽△BAC时,=,
即=,
解得t=2;
当△BPQ∽△BCA时,=,
即=,
解得t=.
答:经过2 s或 s△BPQ和△BAC相似.
11.解:(1)3 Rt△EPB,Rt△PDF,Rt△EAF
(2)答案不唯一,如:选择Rt△EPB.
证明:∵四边形ABCD是正方形,
∴AB∥CD,∴∠EBP=∠BPC.
又∵∠C=∠BPE=90°,
∴Rt△BCP∽Rt△EPB.
12.解:(1)∠APC=∠ACB,∠ACP=∠B(答案不唯一)
(2)如,延长AB到点D,使BD=BC,连接CD.
∵AC2=AB2+AB·BC,
∴AC2=AB(AB+BC)=
AB(AB+BD)=AB·AD,
∴=.
又∵∠A=∠A,
∴△ACB∽△ADC,
∴∠ACB=∠D.
∵BC=BD,∴∠BCD=∠D,
∴∠ACB=∠BCD=∠D.
在△ACD中,
∵∠ACB+∠BCD+∠D+∠A=180°,
∴3∠ACB+30°=180°,
∴∠ACB=50°.
1.如,AD是Rt△ABC斜边上的中线,AE⊥AD交CB的延长线于点E,则中一定相似的三角形是 ( )
A.△AED与△ACB
B.△AEB与△ACD
C.△BAE与△ACE
D.△AEC与△DAC
2.如,AB∥CD,AD,BC相交于点O,E,F分别是OA,OB的中点.若OB=4,OC=3,EF=4,则CD的长为 ( )
A. B.4 C.6 D.8
3.如,点D,E分别在△ABC的AB,AC边上,增加下列条件中的一个:①∠AED=∠B;②∠ADE=∠C;③=;④=;⑤AC2=AD·AE,能使△ADE与△ACB一定相似的有 ( )
A.①②④ B.②④⑤
C.①②③④ D.①②③⑤
4.如,等边三角形ABC的边长为3,P为BC边上一点,且BP=1,D为AC边上一点.若∠APD=60°,则CD的长为 ( )
A. B. C. D.1
5.如,在△ABC中,∠ACB=90°,CD是斜边AB上的高,AD=9,BD=4,那么CD= ,AC= .
6.[2020·海淀区期末] 如,在△ABC与△ADE中,=,且∠EAC=∠DAB.
求证:△ABC∽△ADE.
7.如,已知∠ACB=∠CBD=90°,AC=4 cm,BC=3 cm,那么BD为多少时,△ACB与△CBD相似
8.[2020·西城区期末] 如,在△ABC中,AD平分∠BAC,E是AD上一点,且BE=BD.
(1)求证:△ABE∽△ACD;
(2)若BD=1,CD=2,求的值.
9.如,在 ABCD中,E是AB延长线上一点,连接DE,交AC于点G,交BC于点F,请找出中所有相似的三角形(不含全等三角形),任选其中一对进行证明.
10.如,在△ABC中,AB=8 cm,BC=16 cm,点P从点A出发沿AB边向点B以2 cm/s的速度移动,点Q从点B出发沿BC边向点C以4 cm/s的速度移动,如果点P,Q分别从点A,B同时出发,当点Q到达点C时,两点同时停止运动.经过几秒△BPQ和△BAC相似
11.如,将Rt△BPE与正方形ABCD叠放在一起,并使其直角顶点P落在线段CD上(不与C,D两点重合),斜边的一部分与线段AB重合,EP交AD于点F.
(1)中与Rt△BCP相似的三角形共有 个,分别是 ;
(2)请选择第(1)问答案中的任意一个三角形,完成该三角形与Rt△BCP相似的证明.
12.王华在学习相似三角形时,在北京市义务教育教科书九年级上册第31页遇到这样一道题:如①,在△ABC中,P是边AB上的一点,连接CP.要使△ACP∽△ABC,还需要补充的一个条件是 ,或 .
请回答:
(1)王华应补充的条件是 ,或 .
(2)请你参考上面的形和结论,探究、解答下面的问题:
如②,在△ABC中,∠A=30°,AC2=AB2+AB·BC,求∠ACB的度数.
答案
1.C 解: ∵AD是Rt△ABC斜边上的中线,
∴AD=BD=CD,
∴∠C=∠DAC.
∵∠BAE+∠BAD=90°,∠DAC+∠BAD=90°,
∴∠BAE=∠DAC,∴∠C=∠BAE.
又∵∠E=∠E,∴△BAE∽△ACE.
2.C 3.A 4.B 5.6 3
6.证明:∵∠EAC=∠DAB,
∴∠EAC+∠BAE=∠DAB+∠BAE,
∴∠BAC=∠DAE.
又∵=,∴△ABC∽△ADE.
7.解: 此类问题,不能想当然地认为就是△ACB∽△CBD,等角的不同决定了相似三角形对应点的不同,一定要注意分类讨论.
解:∵∠ACB=∠CBD=90°,
∴分以下两种情况讨论.
当△ACB∽△DBC时,
==1,∴DB=AC=4 cm;
当△ACB∽△CBD时,
=,∴DB==(cm).
综上所述,当BD为4 cm或 cm时,△ACB与△CBD相似.
[点评] 中考对数学思想的考查是非常到位的,分类讨论的数学思想是中考考查的重点.
8.解:(1)证明:∵AD平分∠BAC,
∴∠BAE=∠CAD.
∵BE=BD,∴∠BED=∠BDE,
∴∠AEB=∠ADC,
∴△ABE∽△ACD.
(2)∵△ABE∽△ACD,
∴=.
∵BE=BD=1,CD=2,
∴=.
9.解:△EFB∽△EDA,△FGC∽△DGA,△EBF∽△DCF,△GAE∽△GCD,△ADE∽△CFD.
选择△EFB∽△EDA进行证明.
证明:∵四边形ABCD是平行四边形,
∴BC∥AD,
∴△EFB∽△EDA.(所选相似三角形不唯一)
10.解:设经过t s△BPQ和△BAC相似.
当△BPQ∽△BAC时,=,
即=,
解得t=2;
当△BPQ∽△BCA时,=,
即=,
解得t=.
答:经过2 s或 s△BPQ和△BAC相似.
11.解:(1)3 Rt△EPB,Rt△PDF,Rt△EAF
(2)答案不唯一,如:选择Rt△EPB.
证明:∵四边形ABCD是正方形,
∴AB∥CD,∴∠EBP=∠BPC.
又∵∠C=∠BPE=90°,
∴Rt△BCP∽Rt△EPB.
12.解:(1)∠APC=∠ACB,∠ACP=∠B(答案不唯一)
(2)如,延长AB到点D,使BD=BC,连接CD.
∵AC2=AB2+AB·BC,
∴AC2=AB(AB+BC)=
AB(AB+BD)=AB·AD,
∴=.
又∵∠A=∠A,
∴△ACB∽△ADC,
∴∠ACB=∠D.
∵BC=BD,∴∠BCD=∠D,
∴∠ACB=∠BCD=∠D.
在△ACD中,
∵∠ACB+∠BCD+∠D+∠A=180°,
∴3∠ACB+30°=180°,
∴∠ACB=50°.
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
