北京课改版数学九年级上册同步课时练习:19.2 第5课时 二次函数y=ax2+bx+c(a≠0)的图象(word版含答案)
文档属性
| 名称 | 北京课改版数学九年级上册同步课时练习:19.2 第5课时 二次函数y=ax2+bx+c(a≠0)的图象(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 489.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-17 00:00:00 | ||
图片预览


文档简介
第5课时 二次函数y=ax2+bx+c(a≠0)的象
对于抛物线y=ax2+bx+c(a≠0).
(1)a,b决定抛物线的对称轴的位置:a,b同号,对称轴在y轴的左侧;a,b异号,对称轴在y轴的右侧.
(2)c决定抛物线与y轴的交点(此时点的横坐标x=0)的位置:当c>0时,抛物线与y轴的交点在y轴的正半轴上;当c=0时,抛物线经过原点;当c<0时,抛物线与y轴的交点在y轴的负半轴上.
(3)将y=ax2+bx+c(a≠0)用配方法可写成y=a2+的形式,其顶点坐标为
.
1.下列关于抛物线y=x2+2x+1的说法正确的是( )
A.开口向下 B.对称轴是直线x=1
C.与x轴有两个交点 D.顶点坐标是(-1,0)
2.二次函数y=ax2+bx+c中,若a>0,b<0,c<0,则象的顶点坐标在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
3.若抛物线y=x2-8x+c的顶点在x轴上,则c的值为 ( )
A.16 B.8 C.4 D.-4
4.二次函数y=x2+bx+c的象先沿x轴向左平移2个单位,再沿y轴向上平移3个单位,得到的象的函数表达式为y=x2-2x+1,则b与c分别等于( )
A.6,4 B.-8,14 C.-6,6 D.-8,-14
5.将二次函数y=x2-2x+3化成y=a(x-h)2+k的形式: ,则该二次函数象的顶点坐标是 .
6.已知二次函数y=x2+bx+8的象与x轴相交于A,B两点,点A的坐标为(-2,0),则点B的坐标是 .
7.若二次函数y=x2+(m-1)x-的象的顶点横坐标是2,则m的值是 .
8.[2020·门头沟区期末] 已知二次函数y=x2-2x-3.
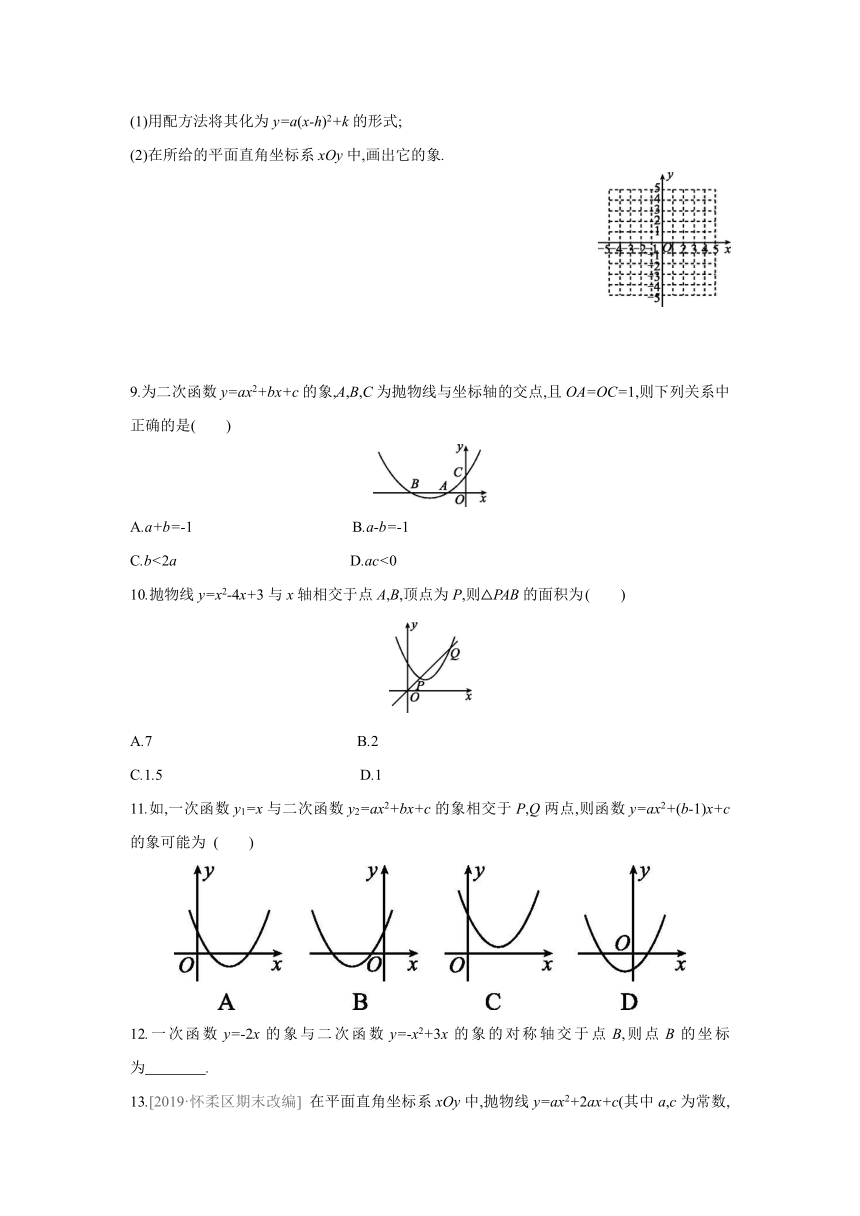
(1)用配方法将其化为y=a(x-h)2+k的形式;
(2)在所给的平面直角坐标系xOy中,画出它的象.
9.为二次函数y=ax2+bx+c的象,A,B,C为抛物线与坐标轴的交点,且OA=OC=1,则下列关系中正确的是( )
A.a+b=-1 B.a-b=-1
C.b<2a D.ac<0
10.抛物线y=x2-4x+3与x轴相交于点A,B,顶点为P,则△PAB的面积为 ( )
A.7 B.2
C.1.5 D.1
11.如,一次函数y1=x与二次函数y2=ax2+bx+c的象相交于P,Q两点,则函数y=ax2+(b-1)x+c的象可能为 ( )
12.一次函数y=-2x的象与二次函数y=-x2+3x的象的对称轴交于点B,则点B的坐标为 .
13.[2019·怀柔区期末改编] 在平面直角坐标系xOy中,抛物线y=ax2+2ax+c(其中a,c为常数,且a<0)与x轴交于点A(-3,0),与y轴交于点B,该抛物线的顶点C到x轴的距离为4.
(1)求抛物线的表达式;
(2)顶点C关于x轴的对称点记为C',求△ABC'的面积.
14.如,已知抛物线y=x2-2x+1 与y轴交于点A,与x轴交于点B.
(1)求点A,B的坐标;
(2)过点A作x轴的平行线,交抛物线于点C.求证:△ABC是等腰直角三角形.
15.[2020·密云区期末] 在平面直角坐标系xOy中,已知抛物线y=ax2-2ax+5a+8(a≠0).
(1)写出抛物线顶点的纵坐标 (用含a的代数式表示).
(2)若该抛物线与x轴的两个交点分别为A和B,且点A在点B的左侧,AB=4.
①求a的值;
②记二次函数象在点A,B之间的部分为W(含点A和点B),若直线y=kx+b(k≠0)经过点(1,-1),且与形W有公共点,结合函数象,求b的取值范围.
答案
1.D 解: a=1,故抛物线的开口向上;将y=x2+2x+1配方,得y=(x+1)2,故抛物线的对称轴是直线x=-1,它与x轴只有一个交点.
2.D
3.A 解: 因为抛物线的顶点在x轴上,所以b2-4ac=0,即64-4c=0,得c=16.
4.C 5.y=(x-1)2+2 (1,2)
6.(-4,0) 解: ∵二次函数y=x2+bx+8的象与x轴交于点A(-2,0),∴0=4-2b+8,解得b=6, ∴二次函数的表达式为y=x2+6x+8,即y=(x+2)(x+4).
∵二次函数y=(x+2)(x+4)的象与x轴的交点坐标为(-2,0)(-4,0),
∴点B的坐标为(-4,0).
7.-3
8.解:(1)y=x2-2x-3=(x-1)2-4.
(2)由(1)知函数象的顶点坐标为(1,-4).
当y=0时,x2-2x-3=0,
(x+1)(x-3)=0,x1=-1,x2=3,
∴函数象与x轴的交点坐标为(-1,0),(3,0).
当y=-3时,x2-2x-3=-3.
解得x1=0,x2=2.
∴函数象经过(0,-3),(2,-3).
画出二次函数象如.
9.B 10.D 11.A 12.
13.解:(1)由题意,得抛物线y=ax2+2ax+c的对称轴是直线x=-=-1.
∵a<0,∴抛物线开口向下.
又∵抛物线与x轴有交点,
∴抛物线的顶点C在x轴的上方.
又∵抛物线顶点C到x轴的距离为4,
∴顶点C的坐标是(-1,4).
可设此抛物线的表达式是y=a(x+1)2+4.
∵此抛物线与x轴的交点A的坐标是(-3,0),
∴a=-1.
因此,抛物线的表达式是y=-x2-2x+3.
(2)结合(1)得C'(-1,-4),B(0,3).
设直线BC'的函数表达式为y=kx+b.
把点B(0,3),C'(-1,-4)代入,易得y=7x+3,则此直线与x轴的交点记为M-,0,
∴AM=,
∴S△ABC'=S△ABM+S△AMC'=9.
14.解:(1)当x=0时,y=1,∴点A的坐标为(0,1).当y=0时,x2-2x+1=0,得x1=x2=1,
∴点B的坐标为(1,0).
(2)证明:∵A(0,1),B(1,0),
∴△AOB是等腰直角三角形,
∴∠OBA=45°.
又∵AC∥OB,∴∠BAC=∠OBA=45°.
由题意可知点A,C关于抛物线的对称轴对称,且点B在对称轴上,
∴AB=BC,
∴∠ACB=∠BAC=45°,则∠ABC=90°,
故△ABC是等腰直角三角形.
15.解:(1)4a+8
(2)①易得抛物线的对称轴是直线x=1.
∵抛物线与x轴的两个交点分别为A和B,AB=4,
∴点A和点B各距离对称轴2个单位.
∵点A在点B的左侧,
∴A(-1,0),B(3,0).
将B(3,0)代入y=ax2-2ax+5a+8,
得9a-6a+5a+8=0,
∴a=-1.
②如,当y=kx+b(k≠0)经过点(1,-1)和点A(-1,0)时,
解得b=-;
当y=kx+b(k≠0)经过点(1,-1)和点B(3,0)时,解得b=-.
结合象可知b≥-或b≤-.
对于抛物线y=ax2+bx+c(a≠0).
(1)a,b决定抛物线的对称轴的位置:a,b同号,对称轴在y轴的左侧;a,b异号,对称轴在y轴的右侧.
(2)c决定抛物线与y轴的交点(此时点的横坐标x=0)的位置:当c>0时,抛物线与y轴的交点在y轴的正半轴上;当c=0时,抛物线经过原点;当c<0时,抛物线与y轴的交点在y轴的负半轴上.
(3)将y=ax2+bx+c(a≠0)用配方法可写成y=a2+的形式,其顶点坐标为
.
1.下列关于抛物线y=x2+2x+1的说法正确的是( )
A.开口向下 B.对称轴是直线x=1
C.与x轴有两个交点 D.顶点坐标是(-1,0)
2.二次函数y=ax2+bx+c中,若a>0,b<0,c<0,则象的顶点坐标在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
3.若抛物线y=x2-8x+c的顶点在x轴上,则c的值为 ( )
A.16 B.8 C.4 D.-4
4.二次函数y=x2+bx+c的象先沿x轴向左平移2个单位,再沿y轴向上平移3个单位,得到的象的函数表达式为y=x2-2x+1,则b与c分别等于( )
A.6,4 B.-8,14 C.-6,6 D.-8,-14
5.将二次函数y=x2-2x+3化成y=a(x-h)2+k的形式: ,则该二次函数象的顶点坐标是 .
6.已知二次函数y=x2+bx+8的象与x轴相交于A,B两点,点A的坐标为(-2,0),则点B的坐标是 .
7.若二次函数y=x2+(m-1)x-的象的顶点横坐标是2,则m的值是 .
8.[2020·门头沟区期末] 已知二次函数y=x2-2x-3.
(1)用配方法将其化为y=a(x-h)2+k的形式;
(2)在所给的平面直角坐标系xOy中,画出它的象.
9.为二次函数y=ax2+bx+c的象,A,B,C为抛物线与坐标轴的交点,且OA=OC=1,则下列关系中正确的是( )
A.a+b=-1 B.a-b=-1
C.b<2a D.ac<0
10.抛物线y=x2-4x+3与x轴相交于点A,B,顶点为P,则△PAB的面积为 ( )
A.7 B.2
C.1.5 D.1
11.如,一次函数y1=x与二次函数y2=ax2+bx+c的象相交于P,Q两点,则函数y=ax2+(b-1)x+c的象可能为 ( )
12.一次函数y=-2x的象与二次函数y=-x2+3x的象的对称轴交于点B,则点B的坐标为 .
13.[2019·怀柔区期末改编] 在平面直角坐标系xOy中,抛物线y=ax2+2ax+c(其中a,c为常数,且a<0)与x轴交于点A(-3,0),与y轴交于点B,该抛物线的顶点C到x轴的距离为4.
(1)求抛物线的表达式;
(2)顶点C关于x轴的对称点记为C',求△ABC'的面积.
14.如,已知抛物线y=x2-2x+1 与y轴交于点A,与x轴交于点B.
(1)求点A,B的坐标;
(2)过点A作x轴的平行线,交抛物线于点C.求证:△ABC是等腰直角三角形.
15.[2020·密云区期末] 在平面直角坐标系xOy中,已知抛物线y=ax2-2ax+5a+8(a≠0).
(1)写出抛物线顶点的纵坐标 (用含a的代数式表示).
(2)若该抛物线与x轴的两个交点分别为A和B,且点A在点B的左侧,AB=4.
①求a的值;
②记二次函数象在点A,B之间的部分为W(含点A和点B),若直线y=kx+b(k≠0)经过点(1,-1),且与形W有公共点,结合函数象,求b的取值范围.
答案
1.D 解: a=1,故抛物线的开口向上;将y=x2+2x+1配方,得y=(x+1)2,故抛物线的对称轴是直线x=-1,它与x轴只有一个交点.
2.D
3.A 解: 因为抛物线的顶点在x轴上,所以b2-4ac=0,即64-4c=0,得c=16.
4.C 5.y=(x-1)2+2 (1,2)
6.(-4,0) 解: ∵二次函数y=x2+bx+8的象与x轴交于点A(-2,0),∴0=4-2b+8,解得b=6, ∴二次函数的表达式为y=x2+6x+8,即y=(x+2)(x+4).
∵二次函数y=(x+2)(x+4)的象与x轴的交点坐标为(-2,0)(-4,0),
∴点B的坐标为(-4,0).
7.-3
8.解:(1)y=x2-2x-3=(x-1)2-4.
(2)由(1)知函数象的顶点坐标为(1,-4).
当y=0时,x2-2x-3=0,
(x+1)(x-3)=0,x1=-1,x2=3,
∴函数象与x轴的交点坐标为(-1,0),(3,0).
当y=-3时,x2-2x-3=-3.
解得x1=0,x2=2.
∴函数象经过(0,-3),(2,-3).
画出二次函数象如.
9.B 10.D 11.A 12.
13.解:(1)由题意,得抛物线y=ax2+2ax+c的对称轴是直线x=-=-1.
∵a<0,∴抛物线开口向下.
又∵抛物线与x轴有交点,
∴抛物线的顶点C在x轴的上方.
又∵抛物线顶点C到x轴的距离为4,
∴顶点C的坐标是(-1,4).
可设此抛物线的表达式是y=a(x+1)2+4.
∵此抛物线与x轴的交点A的坐标是(-3,0),
∴a=-1.
因此,抛物线的表达式是y=-x2-2x+3.
(2)结合(1)得C'(-1,-4),B(0,3).
设直线BC'的函数表达式为y=kx+b.
把点B(0,3),C'(-1,-4)代入,易得y=7x+3,则此直线与x轴的交点记为M-,0,
∴AM=,
∴S△ABC'=S△ABM+S△AMC'=9.
14.解:(1)当x=0时,y=1,∴点A的坐标为(0,1).当y=0时,x2-2x+1=0,得x1=x2=1,
∴点B的坐标为(1,0).
(2)证明:∵A(0,1),B(1,0),
∴△AOB是等腰直角三角形,
∴∠OBA=45°.
又∵AC∥OB,∴∠BAC=∠OBA=45°.
由题意可知点A,C关于抛物线的对称轴对称,且点B在对称轴上,
∴AB=BC,
∴∠ACB=∠BAC=45°,则∠ABC=90°,
故△ABC是等腰直角三角形.
15.解:(1)4a+8
(2)①易得抛物线的对称轴是直线x=1.
∵抛物线与x轴的两个交点分别为A和B,AB=4,
∴点A和点B各距离对称轴2个单位.
∵点A在点B的左侧,
∴A(-1,0),B(3,0).
将B(3,0)代入y=ax2-2ax+5a+8,
得9a-6a+5a+8=0,
∴a=-1.
②如,当y=kx+b(k≠0)经过点(1,-1)和点A(-1,0)时,
解得b=-;
当y=kx+b(k≠0)经过点(1,-1)和点B(3,0)时,解得b=-.
结合象可知b≥-或b≤-.
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
