北京课改版数学九年级上册同步课时练习:19.6 第2课时 反比例函数和一次函数 (word版含答案)
文档属性
| 名称 | 北京课改版数学九年级上册同步课时练习:19.6 第2课时 反比例函数和一次函数 (word版含答案) | 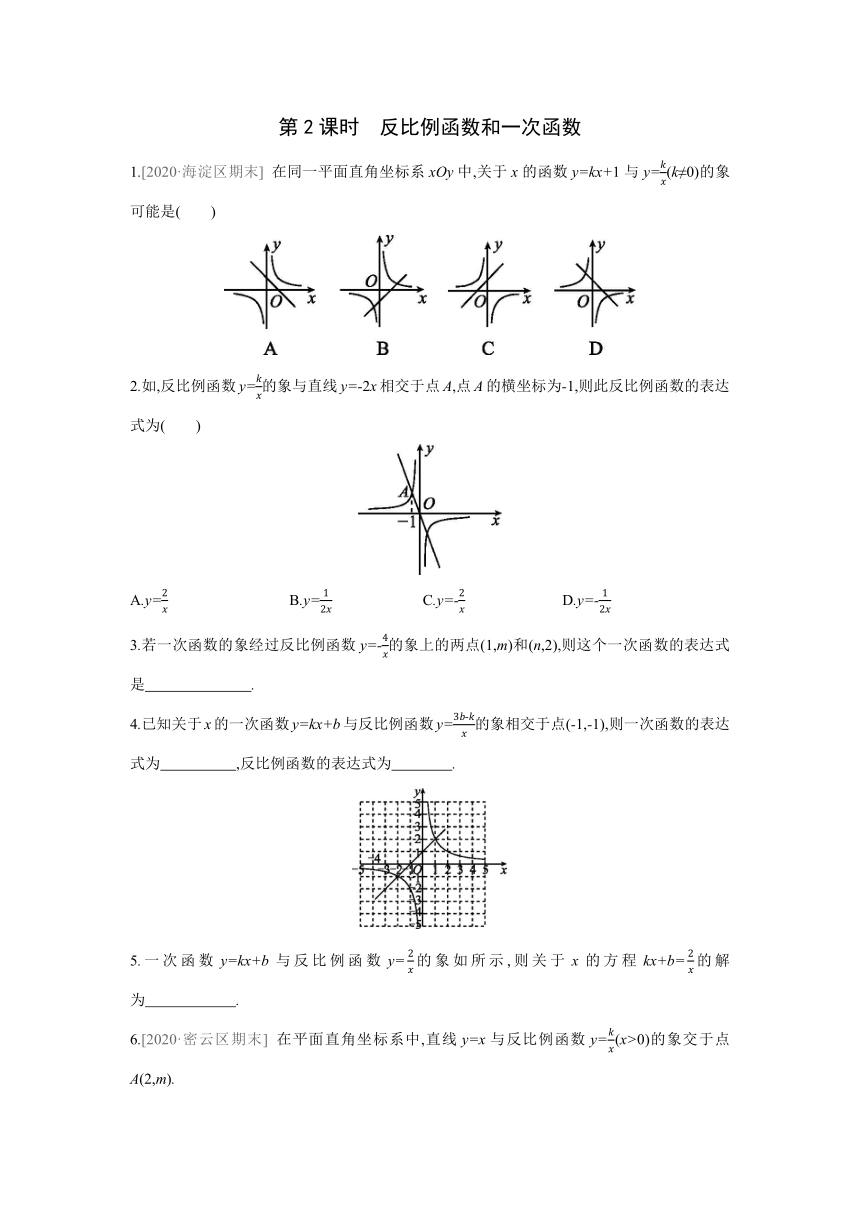 | |
| 格式 | docx | ||
| 文件大小 | 544.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-18 06:56:27 | ||
图片预览



文档简介
第2课时 反比例函数和一次函数
1.[2020·海淀区期末] 在同一平面直角坐标系xOy中,关于x的函数y=kx+1与y=(k≠0)的象可能是( )
2.如,反比例函数y=的象与直线y=-2x相交于点A,点A的横坐标为-1,则此反比例函数的表达式为( )
A.y= B.y= C.y=- D.y=-
3.若一次函数的象经过反比例函数y=-的象上的两点(1,m)和(n,2),则这个一次函数的表达式是 .
4.已知关于x的一次函数y=kx+b与反比例函数y=的象相交于点(-1,-1),则一次函数的表达式为 ,反比例函数的表达式为 .
5.一次函数y=kx+b与反比例函数y=的象如所示,则关于x的方程kx+b=的解为 .
6.[2020·密云区期末] 在平面直角坐标系中,直线y=x与反比例函数y=(x>0)的象交于点A(2,m).
(1)求m和k的值.
(2)P(xP,yP)是函数y=(x>0)象上的任意一点,过点P作平行于x轴的直线,交直线y=x于点B.
①当yP=4时,求线段BP的长;
②当BP≥3时,结合函数象,直接写出点P的纵坐标yP的取值范围.
7.[2020·平谷区期末] 如,在平面直角坐标系xOy中,曲线y=(x>0)经过点A.
(1)求曲线y=(x>0)的函数表达式.
(2)直线y=ax+3(a≠0)与曲线y=(x>0)围成的封闭区域为象G.
①当a=-1时,直接写出象G上的整点个数: ;(注:横、纵坐标均为整数的点称为整点,象G包含边界)
②当象G内只有3个整点时,直接写出a的取值范围.
8.[2020·门头沟区期末] 在平面直角坐标系xOy中,直线y=x与双曲线y=(k≠0)交于点A(2,a).
(1)求a与k的值;
(2)在中画出双曲线y=(k≠0);
(3)设P(m,n)是双曲线y=(k≠0)上一点(点P与点A不重合),直线PA与y轴交于点B(0,b),当AB=2BP时,结合象,直接写出b的值.
9.函数y1=x(x≥0),y2=(x>0)的象如所示,有下面几个结论:
①两函数象的交点A的坐标为(2,2);
②当x>2时,y2>y1;
③直线x=1与函数y2,y1的象分别交于点B,C,则BC=3;
④当x逐渐增大时,y1随着x的增大而增大,y2随着x的增大而减小.
其中正确结论的序号是 .
10.关于x的一次函数y=kx+5与反比例函数y=的象的一个交点的坐标为(-2,3),则另一个交点的坐标为 .
11.[2020·东城区一模] 如,一次函数y=kx+b(k≠0)的象与反比例函数y=(m≠0,x>0)的象在第一象限内交于点A,B,且该一次函数的象与y轴正半轴交于点C,过点A,B分别作y轴的垂线,垂足分别为D,E.已知A(1,4),=.
(1)求m的值和一次函数的表达式;
(2)若M为反比例函数象上在点A,B之间的动点,作射线OM交直线AB于点N,当MN长度最大时,直接写出点M的坐标.
12.[2020·西城区一模] 在平面直角坐标系xOy中,直线l1:y=kx+2k(k>0)与x轴交于点A,与y轴交于点B,与函数y=(x>0)的象的交点P位于第一象限.
(1)若点P的坐标为(1,6).
①求m的值及点A的坐标;
②= .
(2)直线l2:y=2kx-2与y轴交于点C,与直线l1交于点Q,若点P的横坐标为1.
①写出点P的坐标(用含k的式子表示);
②当PQ≤PA时,求m的取值范围.
答案
1.D 2.C 3.y=-2x-2
4.y=2x+1 y= 解: 根据题意,得方程组解得
5.x1=1,x2=-2 解: 由题,可知一次函数y=kx+b与反比例函数y=的象交于点(1,2),(-2,-1),则关于x的方程kx+b=的解是交点的横坐标,即它的解为x1=1,x2=-2.
6.解:(1)m=2,k=4.
(2)①当yP=4时,
点P和点B的纵坐标都为4,
将y=4分别代入到y=和y=x,
可得P(1,4),B(4,4),
∴BP=4-1=3.
②象略.yP≥4或07.解:(1)由题知点A的坐标为(1,1),将其代入曲线表达式y=,得k=1,
∴曲线的函数表达式为y=.
(2)①当a=-1时,直线的函数表达式为y=-x+3,如所示,象G上的整点有(1,1),(2,1),(1,2),共有3个.
故答案为3.
②当直线经过点(3,1)时,有3a+3=1,
解得a=-.
如.作出y=-x+3的象.观察象可知当象G内只有3个整点时,a的取值范围是-1≤a<-.
8.解:(1)把A(2,a)代入y=x得a=2,
则A(2,2).
把A(2,2)代入y=得k=2×2=4.
(2)如所示.
(3)b的值为-2或6.
9.①③④ 10.(-3,2)
11.解:(1)将点A(1,4)代入y=,
得m=4.
∴反比例函数的表达式为y=.
∵BE⊥y轴,AD⊥y轴,
∴∠CEB=∠CDA=90°.
又∵∠ACD=∠BCE,
∴△CDA∽△CEB.∴=.
∵=,∴BE=4AD.
∵A(1,4),∴AD=1.∴BE=4.∴xB=4.
将xB=4代入y=,得yB=1.
∴B(4,1).
将A(1,4),B(4,1)代入y=kx+b,
得解得
∴一次函数的表达式为y=-x+5.
(2)∵点A与点B关于直线y=x对称,反比例函数y=的象关于直线y=x对称,
∴当射线OM的表达式为y=x时,MN的长度最大.
解方程组得或(舍去)
∴此时点M的坐标为(2,2).
12.解:(1)①令y=0,则kx+2k=0.
∵k>0,解得x=-2,
∴点A的坐标为(-2,0).
∵点P的坐标为(1,6),∴m=6.
②
(2)①P(1,3k).
②令kx+2k=2kx-2,解得x=2+.
∴点Q的横坐标为2+.
∵k>0,∴2+>1,
∴点Q在点P的右侧.
如,分别过点P,Q作PM⊥x轴于点M,QN⊥x轴于点N,
则PM∥QN,点M,点N的横坐标分别为1,2+.∴=.
∵PQ≤PA,∴≤1,则=≤1.
又∵k>0,∴k≥1.
∵点P在函数y=的象上,∴P(1,m).
又∵P(1,3k),∴m=3k,
∴m≥3.
1.[2020·海淀区期末] 在同一平面直角坐标系xOy中,关于x的函数y=kx+1与y=(k≠0)的象可能是( )
2.如,反比例函数y=的象与直线y=-2x相交于点A,点A的横坐标为-1,则此反比例函数的表达式为( )
A.y= B.y= C.y=- D.y=-
3.若一次函数的象经过反比例函数y=-的象上的两点(1,m)和(n,2),则这个一次函数的表达式是 .
4.已知关于x的一次函数y=kx+b与反比例函数y=的象相交于点(-1,-1),则一次函数的表达式为 ,反比例函数的表达式为 .
5.一次函数y=kx+b与反比例函数y=的象如所示,则关于x的方程kx+b=的解为 .
6.[2020·密云区期末] 在平面直角坐标系中,直线y=x与反比例函数y=(x>0)的象交于点A(2,m).
(1)求m和k的值.
(2)P(xP,yP)是函数y=(x>0)象上的任意一点,过点P作平行于x轴的直线,交直线y=x于点B.
①当yP=4时,求线段BP的长;
②当BP≥3时,结合函数象,直接写出点P的纵坐标yP的取值范围.
7.[2020·平谷区期末] 如,在平面直角坐标系xOy中,曲线y=(x>0)经过点A.
(1)求曲线y=(x>0)的函数表达式.
(2)直线y=ax+3(a≠0)与曲线y=(x>0)围成的封闭区域为象G.
①当a=-1时,直接写出象G上的整点个数: ;(注:横、纵坐标均为整数的点称为整点,象G包含边界)
②当象G内只有3个整点时,直接写出a的取值范围.
8.[2020·门头沟区期末] 在平面直角坐标系xOy中,直线y=x与双曲线y=(k≠0)交于点A(2,a).
(1)求a与k的值;
(2)在中画出双曲线y=(k≠0);
(3)设P(m,n)是双曲线y=(k≠0)上一点(点P与点A不重合),直线PA与y轴交于点B(0,b),当AB=2BP时,结合象,直接写出b的值.
9.函数y1=x(x≥0),y2=(x>0)的象如所示,有下面几个结论:
①两函数象的交点A的坐标为(2,2);
②当x>2时,y2>y1;
③直线x=1与函数y2,y1的象分别交于点B,C,则BC=3;
④当x逐渐增大时,y1随着x的增大而增大,y2随着x的增大而减小.
其中正确结论的序号是 .
10.关于x的一次函数y=kx+5与反比例函数y=的象的一个交点的坐标为(-2,3),则另一个交点的坐标为 .
11.[2020·东城区一模] 如,一次函数y=kx+b(k≠0)的象与反比例函数y=(m≠0,x>0)的象在第一象限内交于点A,B,且该一次函数的象与y轴正半轴交于点C,过点A,B分别作y轴的垂线,垂足分别为D,E.已知A(1,4),=.
(1)求m的值和一次函数的表达式;
(2)若M为反比例函数象上在点A,B之间的动点,作射线OM交直线AB于点N,当MN长度最大时,直接写出点M的坐标.
12.[2020·西城区一模] 在平面直角坐标系xOy中,直线l1:y=kx+2k(k>0)与x轴交于点A,与y轴交于点B,与函数y=(x>0)的象的交点P位于第一象限.
(1)若点P的坐标为(1,6).
①求m的值及点A的坐标;
②= .
(2)直线l2:y=2kx-2与y轴交于点C,与直线l1交于点Q,若点P的横坐标为1.
①写出点P的坐标(用含k的式子表示);
②当PQ≤PA时,求m的取值范围.
答案
1.D 2.C 3.y=-2x-2
4.y=2x+1 y= 解: 根据题意,得方程组解得
5.x1=1,x2=-2 解: 由题,可知一次函数y=kx+b与反比例函数y=的象交于点(1,2),(-2,-1),则关于x的方程kx+b=的解是交点的横坐标,即它的解为x1=1,x2=-2.
6.解:(1)m=2,k=4.
(2)①当yP=4时,
点P和点B的纵坐标都为4,
将y=4分别代入到y=和y=x,
可得P(1,4),B(4,4),
∴BP=4-1=3.
②象略.yP≥4或0
∴曲线的函数表达式为y=.
(2)①当a=-1时,直线的函数表达式为y=-x+3,如所示,象G上的整点有(1,1),(2,1),(1,2),共有3个.
故答案为3.
②当直线经过点(3,1)时,有3a+3=1,
解得a=-.
如.作出y=-x+3的象.观察象可知当象G内只有3个整点时,a的取值范围是-1≤a<-.
8.解:(1)把A(2,a)代入y=x得a=2,
则A(2,2).
把A(2,2)代入y=得k=2×2=4.
(2)如所示.
(3)b的值为-2或6.
9.①③④ 10.(-3,2)
11.解:(1)将点A(1,4)代入y=,
得m=4.
∴反比例函数的表达式为y=.
∵BE⊥y轴,AD⊥y轴,
∴∠CEB=∠CDA=90°.
又∵∠ACD=∠BCE,
∴△CDA∽△CEB.∴=.
∵=,∴BE=4AD.
∵A(1,4),∴AD=1.∴BE=4.∴xB=4.
将xB=4代入y=,得yB=1.
∴B(4,1).
将A(1,4),B(4,1)代入y=kx+b,
得解得
∴一次函数的表达式为y=-x+5.
(2)∵点A与点B关于直线y=x对称,反比例函数y=的象关于直线y=x对称,
∴当射线OM的表达式为y=x时,MN的长度最大.
解方程组得或(舍去)
∴此时点M的坐标为(2,2).
12.解:(1)①令y=0,则kx+2k=0.
∵k>0,解得x=-2,
∴点A的坐标为(-2,0).
∵点P的坐标为(1,6),∴m=6.
②
(2)①P(1,3k).
②令kx+2k=2kx-2,解得x=2+.
∴点Q的横坐标为2+.
∵k>0,∴2+>1,
∴点Q在点P的右侧.
如,分别过点P,Q作PM⊥x轴于点M,QN⊥x轴于点N,
则PM∥QN,点M,点N的横坐标分别为1,2+.∴=.
∵PQ≤PA,∴≤1,则=≤1.
又∵k>0,∴k≥1.
∵点P在函数y=的象上,∴P(1,m).
又∵P(1,3k),∴m=3k,
∴m≥3.
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
